基于RBF神经网络的景区人流密度预测方法研究
韩娟,潘文佳
(西安职业技术学院,陕西 西安 710077)
旅游业的高速发展造成了人流的过度聚集,产生了一定的安全隐患。因此,各个景区均需准确地监控人流密度的变化,合理调度、引导人流流向,提升游客的旅游体验[1-5]。景区人流密度的预测本质是一个时间序列处理问题,将不同时刻的人流数值以时间维度划分先后并进行排列,即可生成时间序列。在数学上,为了准确描绘时间序列的变化趋势,通常需要引入随机过程理论和相关的统计学方法,从而找到历史数据的变化规律,预测序列的变化。因此,对于时间序列的处理既需要准确把控其历史变化规律,也需要根据这一规律选择合适的预测方法。传统的时间序列处理方法有自回归移动平均模型(ARIMA)和灰度理论模型(GM)。文中将这些方法进行集成,同时利用该方法的残差进行径向基函数(RBF)网络训练,优化了人流密度的预测精度[6-8]。
1 模型设计
1.1 RBF神经网络
近年来,人工神经网络成为了机器学习领域内最常用的算法之一。人工神经网络由互相连接的神经元组成,每个神经元接收上一层神经元发送的信息,并通过非线性变换传送收到的信息,神经网络可以通过训练逼近复杂的映射关系,在模式识别、函数逼近、分类预测上具有广泛的应用[9-14]。
径向基函数(Radial Basis Function,RBF)神经网络是一种特殊的网络结构,其借助RBF进行神经元信息处理,对于非连续的非线性变化具有更优的逼近效果。RBF神经网络的结构如图1所示。
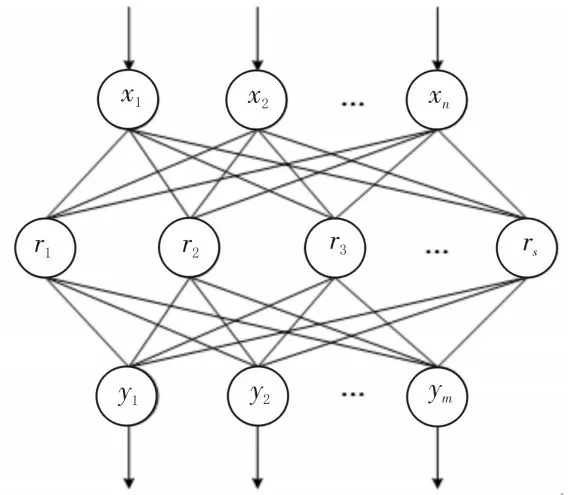
图1 RBF神经网络结构
从图1可以看出,RBF神经网络由输入层xi、隐藏层ri、输出层yi组成。RBF网络的隐藏层采用径向基函数作为非线性变换函数,即:
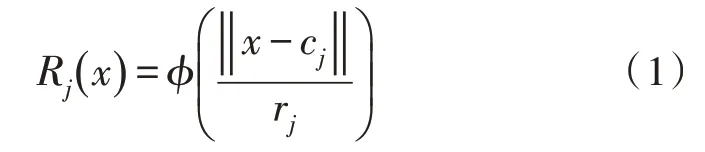
其中,j=1,2,…,s,φ()为该网络使用的径向基函数,常用的函数类型有高斯函数、多二次函数等。对于径向基函数,其主要参数有函数中心cj、半径rj和隐藏层权值wj。在输出层,RBF网络通过线性变换获得输出:
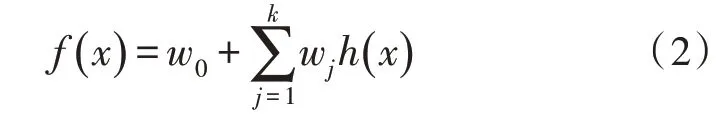
文中在确定函数中心时,使用k-均值法,即:
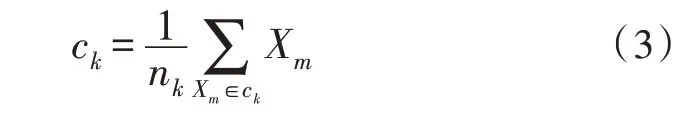
其中,nk是参与训练或测试的样本总数。当类中心的变化小于预设的常数时,聚类停止。
在确定基函数半径时,文中选择固定的函数半径。其确定方法如下:

其中,dmax是确定的函数中心间的最大距离,s是网络中的隐藏节点。RBF网络权值的确定也可以基于梯度下降法进行误差的反向传播,与传统神网络中的算法一致[15-16]。
1.2 时间序列处理模型
从数学上看,人流密度的预测可以归类为时间序列的处理,因此还需引入时间序列处理模型。为了提升模型的预测精度,文中将经典的差分自回归移动平均模型(ARIMA)和灰色生成模型(GM)进行了集成,接下来分别对两种模型进行介绍。
1.2.1 ARIMA模型
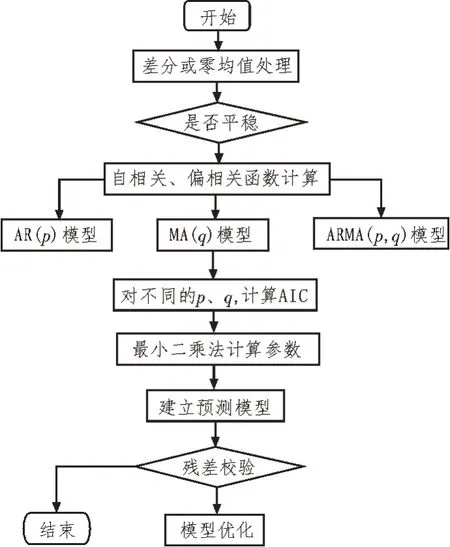
ARIMA模型由AR(p)、MA(q)、ARMA(p,q)3个子部分构成,其中p为自回归项,q为移动平均数,ARMA是对自回归和移动平均的集合。将ARMA差分后,可以得到ARIMA,该模型可准确描绘时间序列的变化。当一个平稳时间序列Xt满足式(4)时,可以建立AR(p)模型:
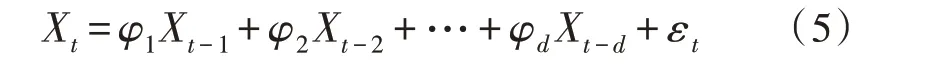
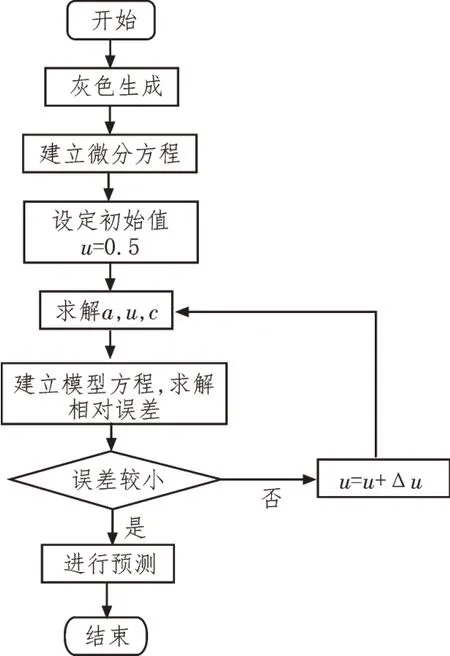
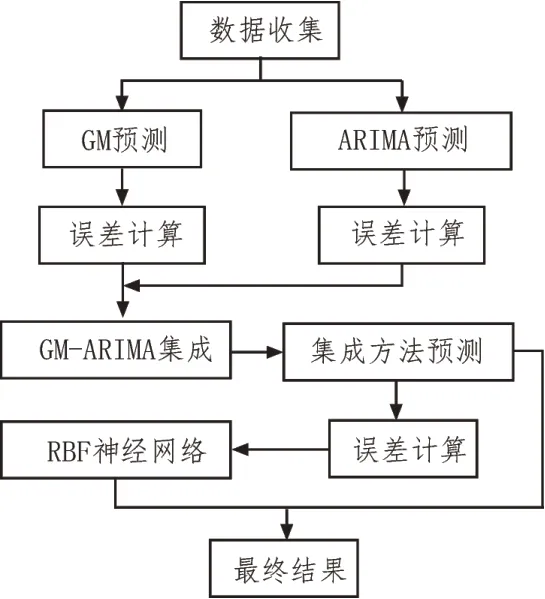
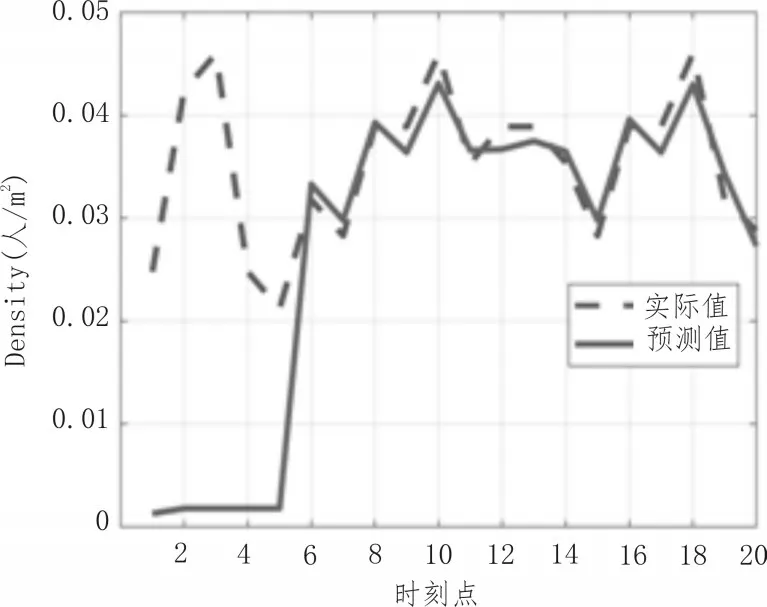
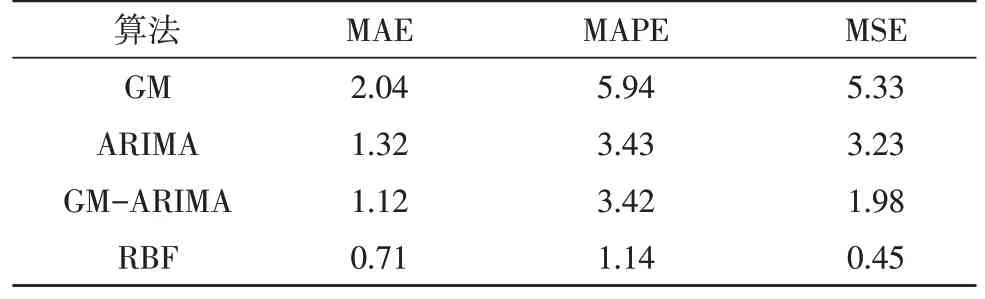
其中,φd为AR()模型的阶数,εt是白噪声。当式(5)对于任意的s 当一个平稳时间序列Xt满足式(5)时,可以建立MA(q)模型: 其中,θd为MA()模型的阶数,εt是白噪声。当式(6)对于任意的s 将AR(p)与MA(q)结合,当满足式(6)时,可以得到ARMA(p,q)模型: 将ARMA(p,q)进行d阶差分,即可得到ARIMA(p,q,d)模型。ARIMA模型建模流程如图2所示。 图2 ARIMA模型建模流程 1.2.2 GM模型 除了ARIMA模型外,灰色预测(GM)算法也是一种常见的时间序列处理方法,GM模型的实现基于微分方程的求解。在建立模型时,需要对时间序列数据进行预处理,获得生成列。通过累加、累减、均值、级比等多种方式生成灰色序列算子,对于原始序列: 其多次累加后的序列为: 其中,m是累加的次数,可以根据时间序列的规律性确定累加的次数。累减与累加互为逆运算,一阶累减的计算方法为: 均值生成有两种:邻均值和非邻均值,前者主要用于等时距的时间序列。在景区的人流序列上,由于数据的缺失,无法满足该条件。因此文中主要使用非邻均值生成,对于原始数据: 其非邻均值生成的结果为: 由于景区的人流数据通常存在端点上的缺失,此时需要引入级比生成进行空穴的填补。对于式(8)给出的原始序列,其级比生成的结果如下: GM模型建模流程如图3所示。 图3 GM模型建模流程 ARIMA和GM算法均可以用于时间序列的分析与预测。在实际应用中,ARIMA算法由于需要对数据进行平稳化处理,削弱数据的趋势,因此对于小时间粒度的时间序列处理能力较弱,而GM算法可以直接进行灰色生成,可以弥补ARIMA算法的劣势。文中进行景区人流密度预测时,对于较大时间间隔的时间序列采用ARIMA算法进行预测;对于较小时间间隔的时间序列使用GM算法进行预测;最后再使用RBF网络对于预测结果的残差进行修正。具体的方法流程如图4所示。 根据图4给出的流程,首先设计数据存储的数据表。在设计数据表时,需要考虑所采集景区的位置、采集的时间,以及基于这些信息的人流密度的初步统计结果。具体的表结构如表1和表2所示。 表1 数据采集表 表2 人流密度初步统计表 图4 文中算法流程图 经过数据采集,文中获得了某景区内连续3个月的整点人流密度数据。基于该数据,即可对该景区的人流密度数据进行预测。在预测时,基于图2给出的流程图,对于该景区使用ARIMA模型以天为间隔进行时间序列建模;基于图3给出的流程图,对于该景区使用GM模型在每一天的时间里以整点为时间间隔进行建模,获得该景区的GM-ARIMA模型。此时,计算该模型的残差序列: 在使用RBF网络时,以每周内的同一时刻作为一个样本对之前采集的数据集进行样本划分。将ε(0)={ε(2),ε(2),…,ε(n)}作为模型的输入样本Xi,基于1.1节中的方法进行模型的RBF函数参数设置。模型训练中使用的误差代价函数如下: 在RBF网络的迭代中,需要根据误差的传播进行连接权值的更新,更新方法如下: 基于1.2、1.3节中ARIMA和GM算法处理时间序列的流程,使用20组数据建立ARIMA-GM模型,并对20组数据进行预测。时间序列的处理结果如表3所示。 表3 时间序列处理结果 根据表3绘制的曲线如图5所示,其中虚线是该景点的实际人流密度,实线为预测值。可以看出,在5个时刻点后,预测值与实际值基本吻合,在前5个时刻略有偏差。 图5 人流密度序列预测结果 接下来,将表3中的残差作为输入数据对RBF进行训练,获得经RBF修正后的预测结果。为了更优地评估算法性能,文中使用平均绝对误差MAE、平均绝对百分比误差MAPE和均方误差MSE作为模型预测的准确度度量指标。同时使用单模型的GM、ARIMA、GM-ARIMA进行对比分析,具体结果如表4所示。 表4 各算法人流密度统计结果对比 可以看出,由于处理的时间序列中大时间粒度的序列占比较高,因此GM算法的性能比ARIMA算法要差;经集成后,GM-ARIMA算法的性能要优于GM和ARIMA算法。文中算法引入RBF算法进行残差修正,获得了最优的预测效果。MAE、MAPE和MSE分别达到了0.71、1.14和0.45,较其他3种算法均有明显的提升。 文中对景区人流密度的预测方法进行了研究,从时间序列处理的角度对该问题进行数学建模,引入ARIMA和GM算法进行时间序列的处理。为了提升传统的时间序列预测的精度,引入RBF对GMARIMA算法处理后的残差进行二次处理,提升了人流预测的精度。实验仿真结果证明,文中的算法具有更高的精度、更优的应用前景。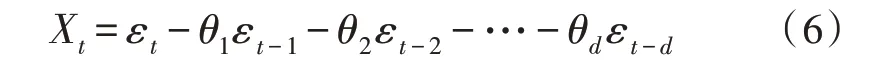
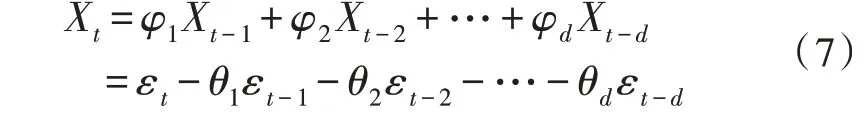
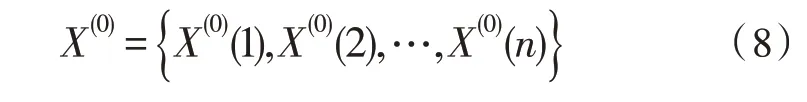
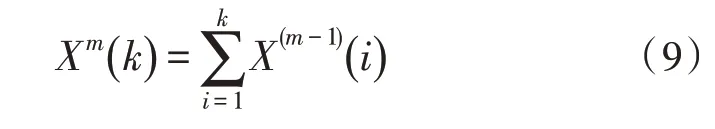
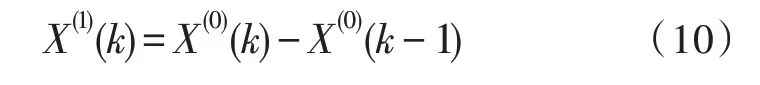
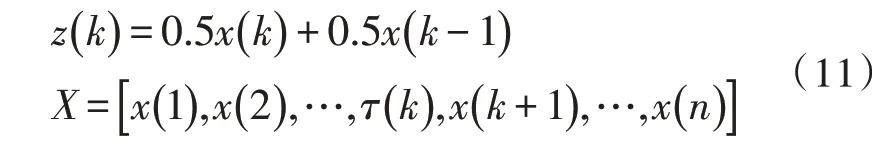
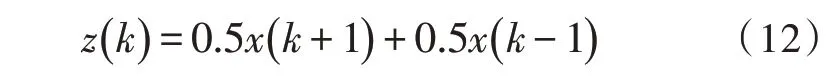
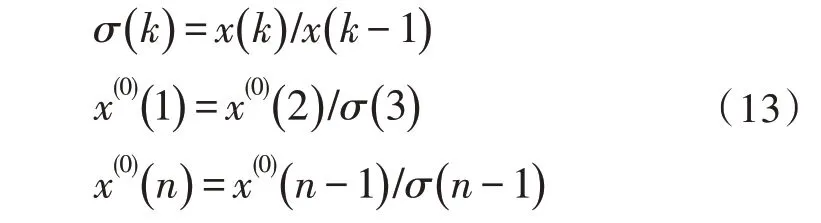
2 方法实现
2.1 实验流程设计


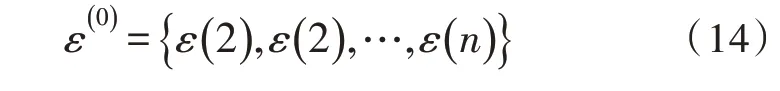
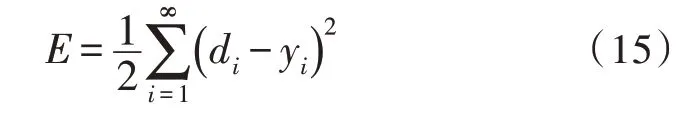
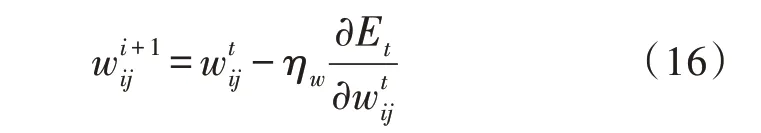
2.2 模型仿真结果

3 结束语

