BP神经网络在新零售行业销售预测中的应用

肖泉彬，黎小龙，车俊俊，何敏

（江西理工大学软件工程学院，江西 南昌 330013）

中国零售市场进入了一个创新与技术应用的高发期[1]，产品供应是市场上最重要的环节之一，准确预测商品销售量从而把握供应量成为企业在市场竞争中存活的关键。随着技术的进步，人工神经网络预测技术在不同领域的应用不断深入[2]，相关学者应用神经网络对临床红细胞用量[3]、血红蛋白浓度[4]、铁路大宗货物运价风险[5]、羊肉价格[6]、滚动轴承故障预测[7]等各个领域进行预测，结果较好。该文在神经网络的基础之上通过Pearson相关性分析，对新零售行业销售量的预测进行应用并得到验证。

1 数据预处理

销售数据预测的准确性取决于过去统计的销售量数据的质量和数量，在数据的收集统计中存在异常情况，需要剔除不完整和异常的数据。如果采用这些数据进行预测，会导致预测成功率下降。由于数据量庞大且数据变量之间相互影响，必须对样本数据进行预处理[8]，对原始数据进行异常值的剔除、相关性分析等。

2 Pearson相关性分析

相关性分析是研究两个及其以上处于同等地位的随机变量之间的相关关系的统计分析方法。相关系数是一种定量描述两组随机变量的统计学相关性的指标。通过比较数组中的每个数对以确定两组数据整体间的相关程度。当自变量取某一值时，因变量对应为一个概率分布，如果对于所有的自变量取值的概率分布都相同，则说明因变量和自变量是没有相关关系的。反之，如果自变量的取值不同，因变量的分布也不同，则说明两者是存在相关关系的。

影响因素既有产品自身的内在因素，也有外部因素[9]，但该文从已知数据入手主要分析库存量、标价、售价与折扣等因素。采用Pearson相关系数分析数据间的相似程度[10]。

原假设为H0∶r=0，则备择假设为H1∶r≠0（其中，r为Pearson相关系数）。

如表1所示，国庆期间，在99%置信水平上，拒绝原假设，Pearson相关系数显著异于0，即销售量与库存、售价相关。

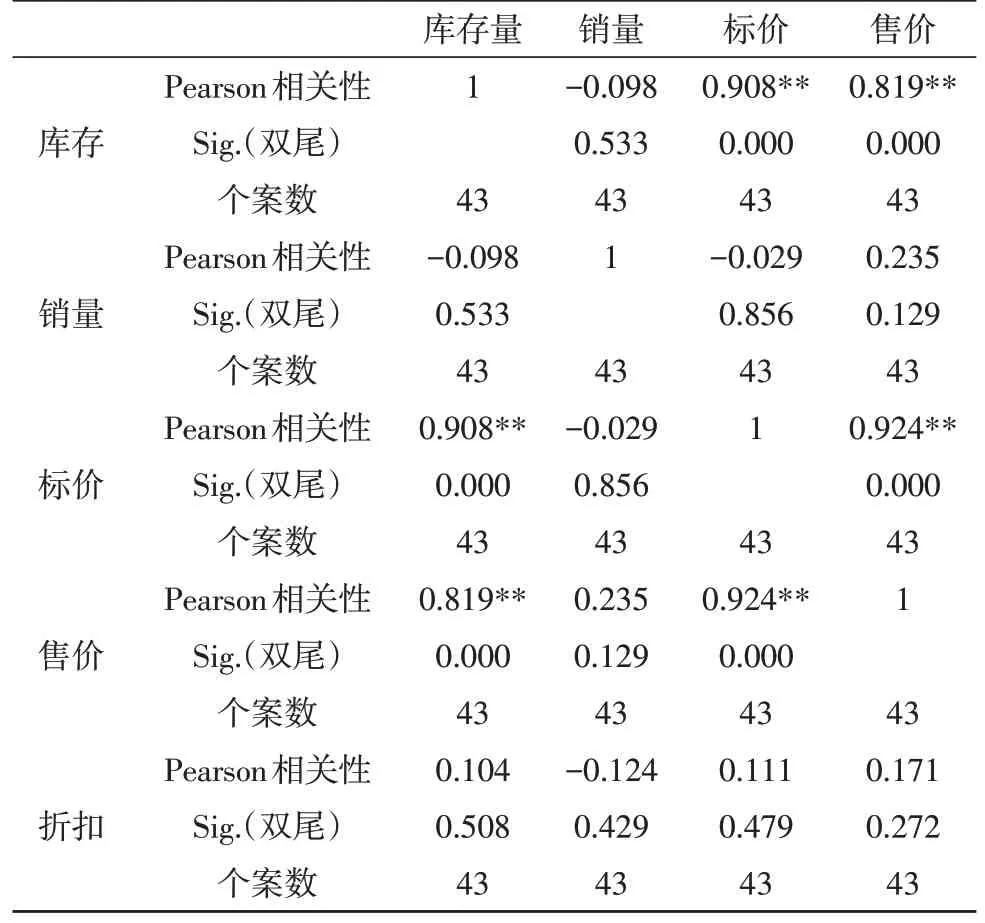
表1 国庆相关性检验

目标单款商品销售量的影响均与其库存、售价相关，与产品的实际价格、节假日的折扣相关性不强[11]。

3 BP神经网络预测模型建立

3.1 输入层和输出层

BP（Back Propagation）神经网络是一种按误差逆传播算法训练的多层前馈网络，其拓扑结构包括输入层、隐含层和输出层，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

BP神经网络的算法具有良好的自适应性和分类识别等能力。其可以看作是一个函数映射，适用于有明确的输入与输出的对应关系，但其中的函数存在不容易确定的问题。而销售量的预测可以看成将相关因素作为输入，销售量为输出的复杂函数映射问题。因此，利用BP神经网络对销售量进行预测。

符号说明如表2所示。

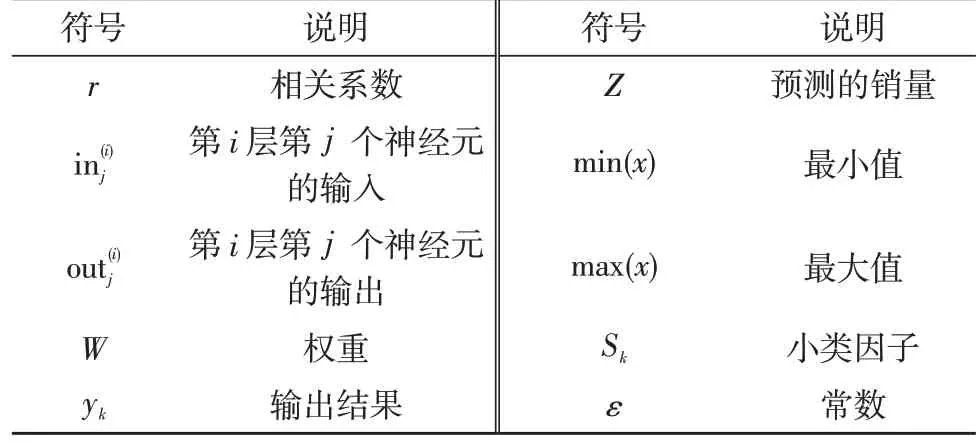
表2 符号说明

输入层:

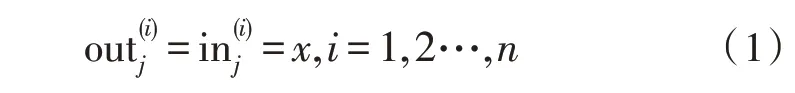
隐含层:

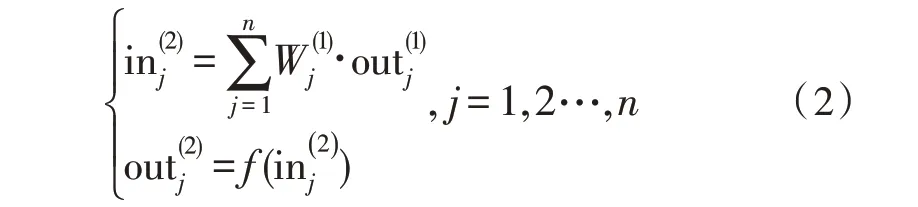
其中，f(x)是激发函数，有多种形式：sigmoid函数、tanh函数、ReLU函数。该文采用sigmoid函数，该函数将取值为(-∞,+∞)的数映射到(0,1)之间。

sigmoid函数为：

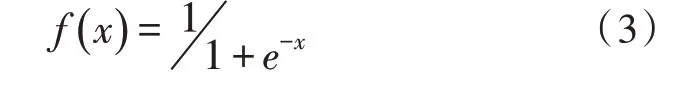
输出层为:

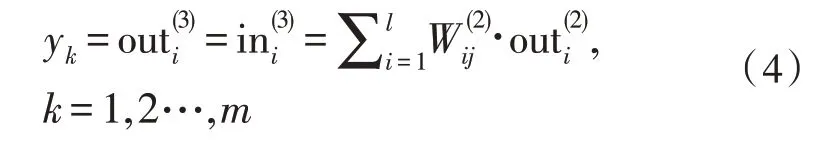
3.2 网络结构设计

3.2.1 输入层和输出层的设计

根据相关性分析得出，影响目标skc销量的因素主要有产品的售价以及产品的库存量。考虑到节假日客流量大，人们的消费欲望明显上涨，所以选取产品售价、库存量以及节假日时长作为网络的输入层节点，商品的销量作为输出节点。故网络结构含有3个输入，1个输出。

3.2.2 隐含层设计

4 BP神经网络预测模型求解

4.1 小类销售预测模型求解

4.1.1 训练样本预处理

由于样本数据[13]中，不同变量之间数值的大小以及量纲不同，需要在训练前进行数据预处理，将所有数据转化在[0,1]范围内，转化方法采用标准化归一化处理[14]。

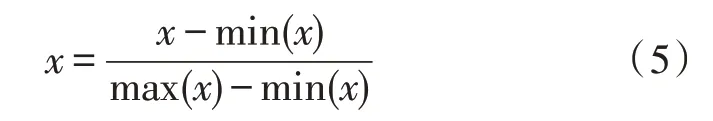
选取对销量有影响的相关因子(售价、库存量)以及节假日时长作为网络的输入。

4.1.2 BP神经网络结构初始化

在确定输入层、隐含层、输出层及相关神经元个数的过程中，该文选取了产品的售价、库存量以及节假日时长，建立图1所示的网络结构，输出节点为目标小类的预测销量[15]。

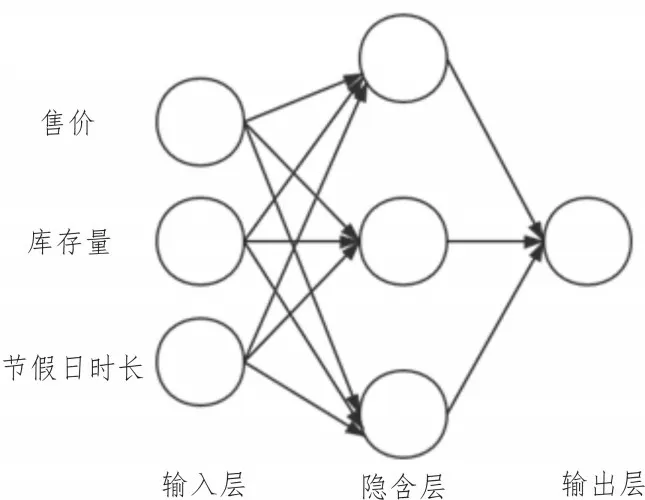
图1 神经网络结构图

4.1.3 生成随机的神经网络的权值与阈值

设定一定大小的迭代次数，以下函数作为相应的训练函数。

输出层误差调整函数为：

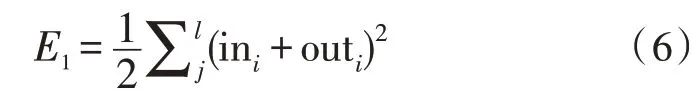
隐含层误差函数为：

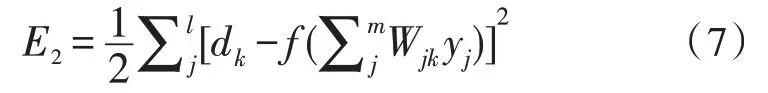
输入层误差函数为：

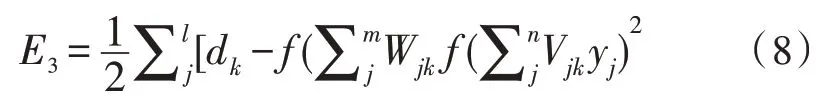
通过输入层、输出层以及隐含层误差函数的反馈，对BP神经网络各节点的权重不断调整优化。算法迭代停止时生成的值为训练目标小类的预测值。

4.2 预测模型的结果

BP神经网络预测模型的结果如图2所示，该图为一个商品小类的预测图形，可以看出，模型的预测值与实际值比较接近，说明神经网络的预测效果良好。

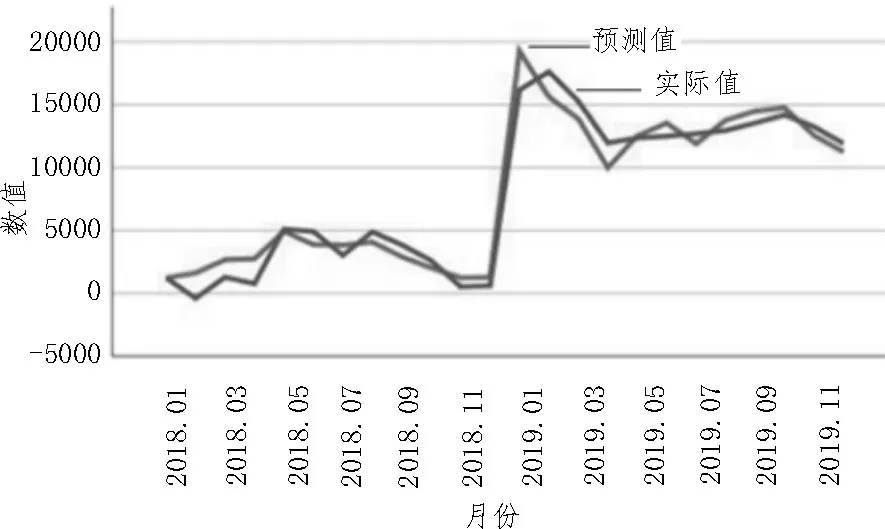
图2 BP神经网络预测模型实际值与预测值

如表3所示，MAPE误差范围小，进一步说明神经网络的预测效果较好。

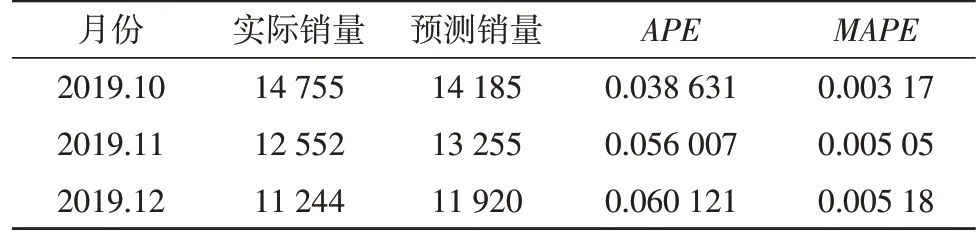
表3 预测商品小类MAPE

5 结束语

建立Pearson相关系数模型，深度挖掘数据之间的联系，再通过BP神经网络预测模型来精准预测市场需求，对商品的销售情况能够较好地预测[16]，可以为新零售行业的库存调配决策工作提供可靠的科学依据。在将来的预测中，应当尽可能地增加样本数据以提高神经网络预测的准确性。