自由曲面机器人摆线抛光轨迹的多参数优化*

倪建龙 王康

学术研究

自由曲面机器人摆线抛光轨迹的多参数优化*

倪建龙 王康

（华南理工大学机械与汽车工程学院，广东 广州 510641）

为获得良好的抛光表面质量，提出一种针对自由曲面的机器人摆线抛光轨迹多参数优化方法。首先，基于人工神经网络建立抛光表面材料去除量分布均匀性预测模型；然后，提出一种基于遗传算法的摆线轨迹多参数组合优化算法；最后，经材料去除量仿真实验和机器人抛光验证，该方法能有效控制抛光表面材料去除量的均匀性，获得较好的镜面抛光效果。

抛光工艺；多参数优化；人工神经网络；遗传算法

0 引言

在曲面抛光工艺中，抛光表面材料去除量分布的均匀性是评价抛光表面质量的重要指标之一。为获得均匀的材料去除量，理想的抛光轨迹不仅实现工件表面的均匀覆盖，避免过抛光和欠抛光现象，还具有良好的多方向特征[1-3]。摆线抛光轨迹可较好地处理以上问题，近年来广泛应用于各种自由曲面的抛光工艺[4-6]。然而，摆线轨迹严格受如图1所示的摆线半径Rcan、摆线步距scan和导线间距scan3个轨迹参数的影响。这3个轨迹参数的不同组合会影响图1中矩形区域一和区域二的材料去除量分布均匀性，且无法通过单一参数调节。目前，实现材料去除量均匀控制的最优摆线轨迹参数的确定主要依赖工人经验和技术手册，需要反复进行大量的抛光实验，不仅耗时耗力，还造成工件原材料较大浪费。

图1 沿着扫描轨迹进给的摆线

为此，本文提出一种针对自由曲面的机器人摆线抛光轨迹多参数优化方法。首先，对抛光表面材料去除量进行仿真；然后，基于人工神经网络建立摆线轨迹参数与抛光表面材料去除量分布均匀性之间的模型；最后，提出一种基于遗传算法的摆线轨迹多参数组合优化算法。

1 材料去除量与抛光轨迹分析

1.1 抛光表面材料去除量模型

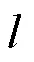
图2 抛光盘与工件之间的接触示意图

根据该应用场景建立的倾斜抛光盘与工件之间的接触压力分布模型如图3所示[7]。当抛光盘与工件平面接触时，接触区域可简化为一条弦和一条圆弧构成的封闭区域（图3(a)）；当抛光盘与工件凸面接触时，接触区域可简化为2个圆弧构成的叶片状区域（图3(b)）；当抛光盘与工件凹面接触时，接触区域可简化为2个圆弧构成的月牙状区域（图3(c)）。

图3 倾斜抛光盘与工件之间的接触压力分布模型

根据上述压力分布模型，可基于Preston方程建立材料去除量模型：

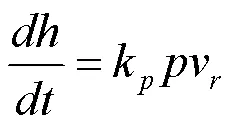
1.2 沿扫描线进给的摆线轨迹分析

沿扫描线进给的摆线轨迹由于具有规划简单和覆盖均匀的特点，被广泛应用于各种自由曲面的抛光，因此本文选用其作为研究对象。为进一步分析上述3个轨迹参数对材料去除量分布的影响规律，对典型的轨迹参数案例进行材料去除量仿真实验，实验中抛光设备参数如表1所示。

表1 仿真实验中抛光设备参数

为保证抛光区域能够均匀覆盖工件表面并获得较高的加工效率，导线间距scan的确定需要考虑具体的抛光盘半径值R。本文将scan限制为

采用本项目组开发的CAM软件实现4个摆线轨迹参数案例的材料去除量仿真实验结果如图4所示。这4个案例使用的摆线轨迹参数如表2所示。由图4(a)可知，如果摆线半径scan较大，同时导线间距scan较小，会导致矩形区域内的轨迹过于密集，造成过抛光现象；相反，如图4(b)所示，如摆线半径scan较小，且导线间距scan较大，会导致矩形区域内的轨迹过于稀疏，造成欠抛光现象；如图4(c)所示，若摆线步距scan设置过小，会导致矩形区域一内的材料去除量明显比区域二内更少；如图4(d)所示，若scan设置过大，则会导致矩形区域内材料去除量比周边区域偏少。

图4 摆线轨迹参数案例的材料去除量仿真实验结果

表2 沿扫描线进给的摆线轨迹参数案例设置值

综合上述分析，本文将摆线半径scan取值范围约束为

另外，为同时满足均匀覆盖和提高加工效率2个要求，摆线半径一般不大于摆线步距且单道摆线轨迹内摆线周期不应过多[8]。

如图5(a)所示，当相邻周期的摆线轨迹相切时，摆线步距和半径之间的近似关系为

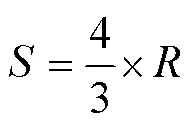
如图5(b)所示，当第一个周期的摆线轨迹和第三个周期的摆线轨迹相切时，摆线步距和半径之间的近似关系为

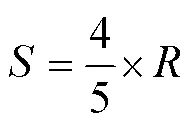
如图5(c)所示，当第一个周期的摆线轨迹和第四个周期的摆线轨迹相切时，摆线步距和半径之间的近似关系为

图5 不同步距和半径的摆线轨迹

为兼顾加工效率与加工质量，将摆线步距和半径之间的关系限定为

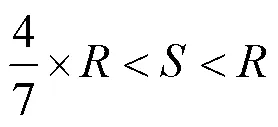
基于以上分析，为获得较好的抛光表面质量，各个摆线轨迹的参数取值范围如表3所示。后续的摆线轨迹参数优化同样需要在这些范围内进行。

表3 沿扫描线进给的摆线参数取值范围

2 摆线轨迹的多参数组合优化

为在表3的区间内实现摆线轨迹的多参数组合优化，本文基于人工神经网络建立抛光表面材料去除量分布均匀性预测模型，并以该模型为适应度函数，提出一种基于遗传算法的摆线轨迹多参数组合优化算法。

2.1 基于人工神经网络的抛光表面材料去除量分布均匀性预测模型

基于人工神经网络建立摆线半径scan、摆线步距scan和导线间距scan3个轨迹参数与抛光表面材料去除量分布均匀性之间的模型。首先，以三角网格模型近似表示工件的曲面模型；然后，将表示工件曲面的三角网格模型输入到本项目组开发的CAM软件进行抛光表面材料去除量仿真，得到三角网格模型各个三角形顶点的抛光表面材料去除量。以各个网格顶点材料去除量的平均值和平方差值作为材料去除量均匀性的评价指标。

本文建立的人工神经网络模型如图6所示，该神经网络为BP神经网络。神经网络的输入为摆线半径scan、摆线步距scan和导线间距scan，输出为所有网格顶点材料去除量的平均值和平方差值。设神经网络的隐藏层为1，隐藏层节点个数为15。

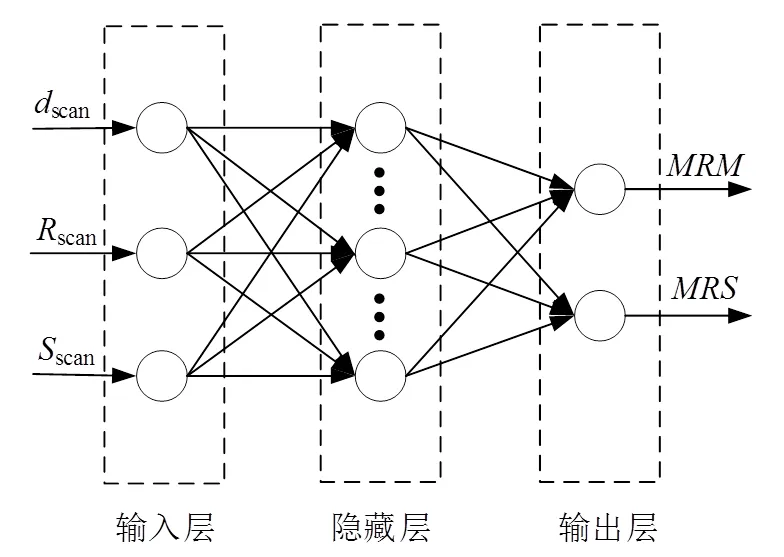
图6 人工神经网络模型

为训练该神经网络，以图7所示复杂曲面模型抛光为例，根据正交实验思想设计25组不同抛光摆线轨迹参数组成的训练集，可较好覆盖轨迹参数组合的大部分情况。这些摆线轨迹参数约束在表3所列的范围内。另外，为了让训练模型的精度更高，本文单独设计700组摆线轨迹参数值随机组合的训练数据集，并设计20组样本组成测试集，以验证训练的人工神经网络的预测精度。

图7 实验工件模型

表4列举了部分不同摆线轨迹参数的仿真和预测结果。人工神经网络模型获得的和的预测值与实际值的比较如图8所示。从图8(a)可以看出，的预测值与实际值曲线非常吻合。从图8(b)可以看出，的预测值和实际值之间存在微小差距，但整体上比较一致。

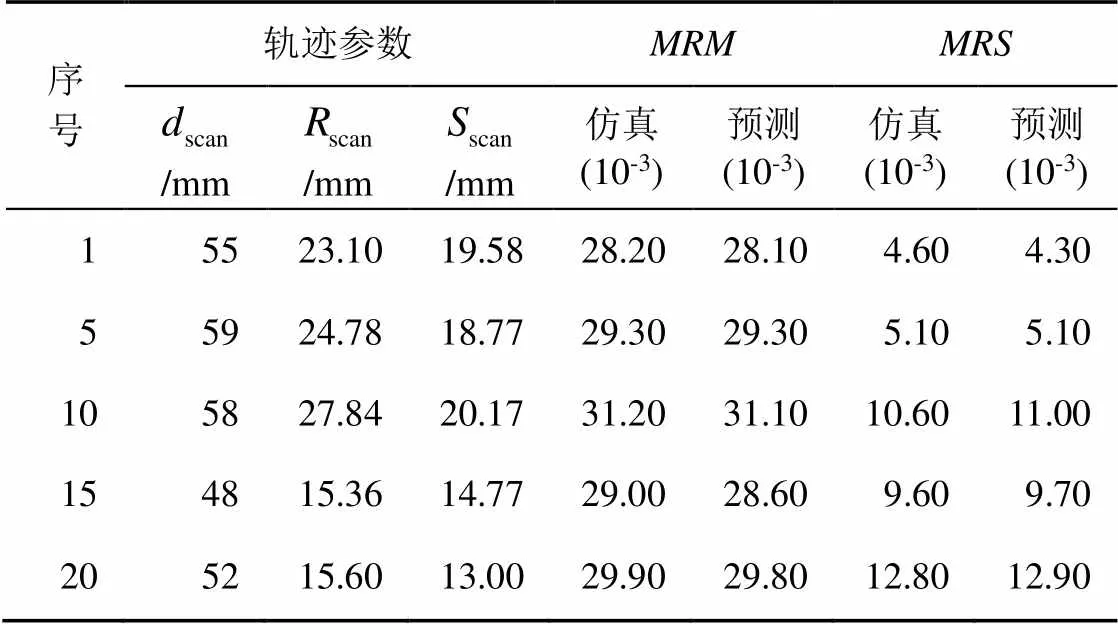
表4 人工神经网络模型仿真和预测结果

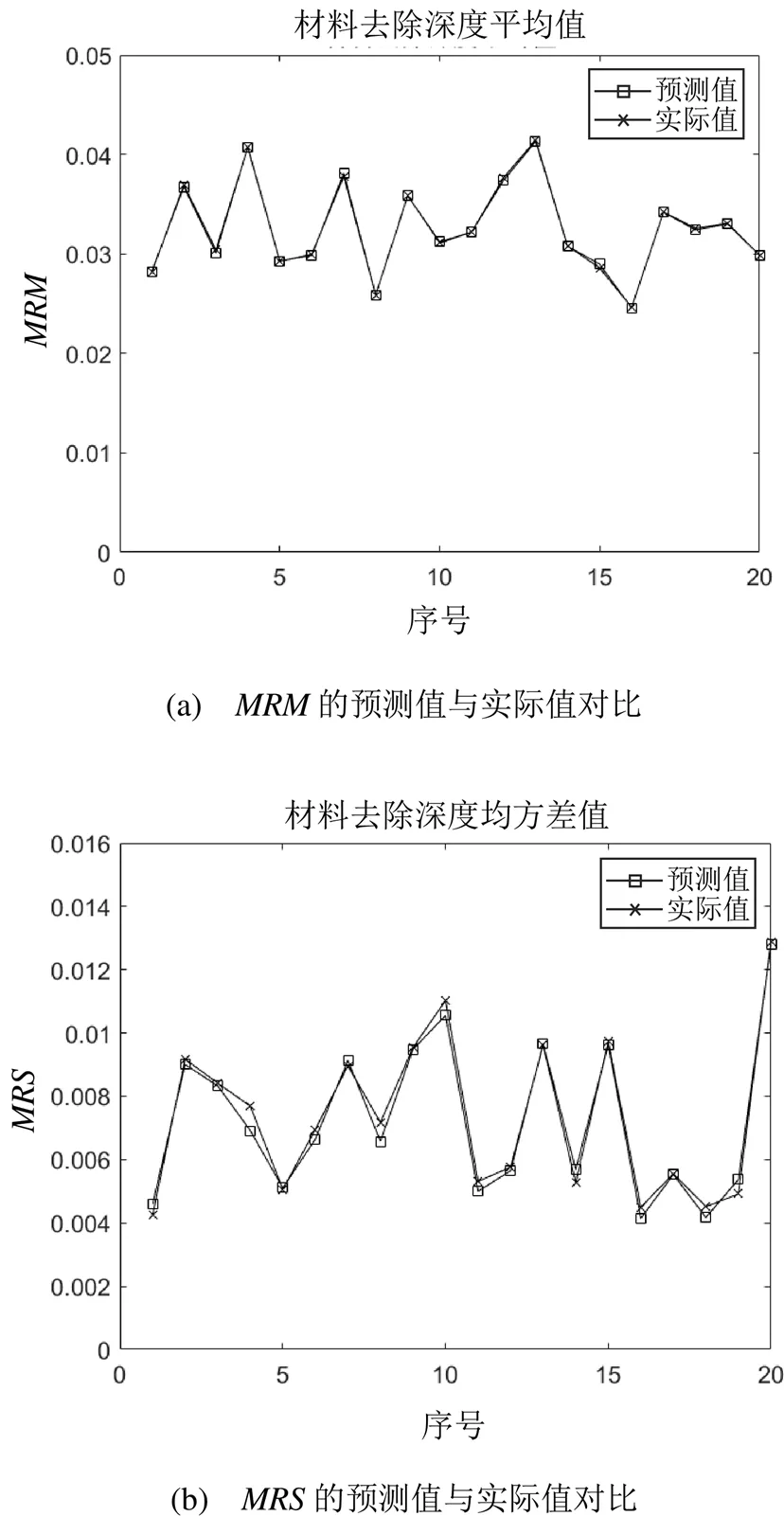
图8 沿扫描线进给的摆线轨迹预测值与实际值对比

2.2 基于遗传算法实现参数组合优化

遗传算法的关键是适应度函数的确定。基于抛光表面材料去除量均匀性分布预测模型，将遗传算法的适应度函数设置为

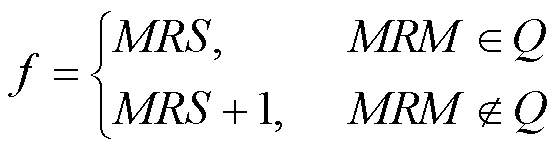
式中，为期望的范围，根据具体工艺要求设置。因为一般远小于1，所以当不在期望的范围内时，可将适应度函数值加1，基于遗传算法策略，这组参数组合会在进化中被淘汰。

利用Matlab的遗传算法工具箱进行实验优化，并将轨迹参数限制在对应的范围内。种群数量设置为50，进化代次数为500，交叉概率为0.6，变异概率为0.02。算法优化具体过程如下：

1）在参数值约束范围内，随机初始化一个种群，并进行编码；

2）对种群进行选择、交叉和变异等操作；

3）使用上文完成训练的人工神经网络模型预测每组的输出参数和，并利用式(8)计算适应度函数，更新种群；

4）判断是否达到最大进化代次数，若是，输出适应度函数最小的参数组合，否则，重复步骤2）。

基于表1的抛光工艺参数，结合本文提出的人工神经网络和遗传算法的摆线轨迹多参数组合优化算法，对沿扫描线进给的摆线轨迹进行轨迹参数优化，并利用材料去除量仿真实验进行论证，得到的最优轨迹参数组合如表5所示。

表5 沿扫描线进给的摆线轨迹最优参数组合

摆线轨迹参数优化后的材料去除量仿真图如图9所示。与图4对比可知，本文提出的算法有效提高了工件抛光表面材料去除量的均匀性。

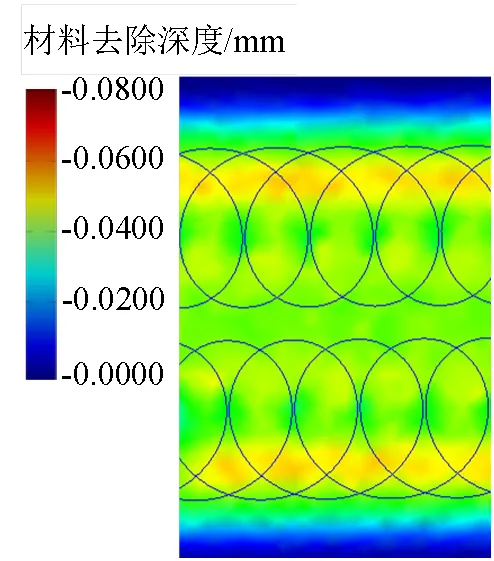
图9 摆线轨迹参数优化后的材料去除量仿真图

3 实验及分析

为验证本文提出的机器人摆线抛光轨迹多参数优化方法的有效性及实用性，设计并开展实际的抛光加工实验。实验采用的自由曲面以及通过本文的方法生成的摆线抛光轨迹和其材料去除量仿真结果如图10所示。机器人抛光实验平台如图11(a)所示，抛光装置为ABB 4600机器人，抛光盘与伺服电机连接在机器人的末端执行器上。抛光工件曲面为图7所示的自由曲面；抛光设备参数与表1一致；摆线轨迹参数与表5一致。首先，抛光盘底部依次附着#400、#600、#800、#1000的砂纸，每种砂纸对工件表面进行2次抛光；然后，利用2.5 μm级的金刚石研磨膏对工件表面进行抛光，最终获得的抛光效果如图11(b)所示。采用本文优化后的摆线轨迹，获得较好的镜面抛光效果，证明本文方法的有效性和实用性。

图10 采用本文方法生成的摆线轨迹

图11 机器人抛光实验

4 结论

本文针对自由曲面提出一种机器人摆线抛光轨迹的多参数组合优化方法。材料去除量仿真实验和实际的机器人抛光实验表明：该方法能够有效控制抛光材料去除量的均匀性，能够获得良好的镜面抛光效果。

[1] TAM H Y, LUI O C, MOK A. Robotic polishing of free-form surfaces using scanning paths[J]. Journal of Materials Processing Technology, 1999, 95(1-3):191-200.

[2] TAM H Y. Toward the uniform coverage of surfaces by scanning curves[J]. Computer-Aided Design, 1999, 31(9):585- 596.

[3] SCHINHAERL M, RASCHER R, STAMP R, et al. Utilisation of time-variant influence functions in the computer controlled polishing[J]. Precision Engineering, 2008, 32(1):47-54.

[4] 谢海龙,许晨旸,王清辉,等.曲面零件机器人抛光轨迹规划与工艺仿真[J].自动化与信息工程,2019,40(6):1-7.

[5] AVRAMPOS P, VOSNIAKOS G C. Coverage in planar surface polishing by trochoidal tool paths[J]. International Journal on Interactive Design and Manufacturing, 2018, 12(2): 663-675.

[6] 王清辉,谢柳杰,许晨旸,等.曲面抛光的材料去除模型与摆线轨迹控制[J].华南理工大学学报(自然科学版),2018,46(3): 8-15.

[7] WANG Q, LIANG Y, XU C, et al. Generation of material removal map for freeform surface polishing with tilted polishing disk[J]. International Journal of Advanced Manufacturing Technology, 2019,102:4213-4226.

[8] JULIEN C, LINARES J, SPRAUEL J. Improving tool wear and surface covering in polishing via toolpath optimization[J]. Journal of Materials Processing Technology, 2013, 213(10): 1661-1668.

Multi-Parameters Optimization of Cycloid Toolpath for Robot Polishing of Freeform Surface

Ni Jianlong Wang Kang

(School of Mechanical and Automotive Engineering，South China University of Technology, Guangzhou 510641, China)

In order to obtain good polishing surface quality, a multi-parameters optimization method of cycloidal polishing toolpath for robot polishing of freeform surfaces is proposed. Firstly, a prediction model of the uniformity of material removal distribution on the polished surface is established based on the artificial neural network. Then, a multi-parameters optimization algorithm of cycloid toolpath based on genetic algorithm is developed. Finally, the simulation experiment of material removal and robot polishing show that this method can effectively control the uniformity of material removal on the polished surface and obtain better mirror polishing effect.

toolpath planning; multi-parameter optimization; artificial neural network; genetic algorithm

倪建龙，男，1991年生，博士研究生在读，助理工程师，主要研究方向：数字化设计与制造。E-mail: nijl@scut.edu.cn

TH161

A

1674-2605(2021)04-0001-06

10.3969/j.issn.1674-2605.2021.04.001

基金项目：广州市重点领域研发计划项目资助（202103020004）