基于电场和流场耦合的FCC油浆脱固性能分析
李 强,李安萌,郭林飞,曹 昊,许伟伟,王振波
(中国石油大学(华东) 新能源学院,山东 青岛 266580)
随着原油重质、劣质化程度日益加剧,催化裂化油浆产量急剧增加。据统计,中国催化裂化(FCC)油浆外甩量在7.5 Mt/a以上[1]。催化裂化油浆中含有大量的催化剂固体颗粒,导致催化裂化装置堵塞及结焦的现象日益严重[2]。另外,FCC油浆中含有大量的稠环芳烃,可用来生产多种高附加值产品[3-7],如炭黑、针状焦和碳纤维等[8]。因此,有效地脱除催化裂化油浆中的固体颗粒对于催化裂化装置安全运行以及生产高附加值产品具有重要的意义。
目前,常用的FCC油浆脱固方法有重力沉降法、旋流分离法、过滤分离法及静电分离法等。其中,静电分离法是利用介电泳技术来实现液-固两相的分离[9-10],具有净化效率高,微小颗粒脱除效果好的优点,广泛应用于石油、化工及医药行业[11]。20世纪50年代,国外成功将静电分离技术用于FCC油浆处理分离装置。美国General Atomics(GA)公司首先开发了轴向型静电分离器[12]。之后,Crissman等[13]和Franse等[14]相继开发了A型和B型径向型静电分离器,较轴向型静电分离器具有线速小、冲刷作用小、横截面大、净化效果高的优点,而B型较A型改进了可拆卸式的反冲洗方式,缩短了装置的运行周期,提高了冲洗效率,因而广泛应用于工业生产。
静态流场下,影响静电分离的因素主要有其结构参数、操作参数和物性参数。结构参数方面,李强等[15]发现,静电分离效率随着填料直径的增大而降低,随着内电极直径的增大先提高后降低;Fritsche等[16]则发现,当填料粒径为3.5~4 mm时,静电分离效率最好;Cao等[17]在利用静电分离煤焦油中的喹啉不溶物时,发现圆柱形电极的分离效率要远高于矩形或梅花形电极的。操作参数方面,赵娜等[18]、方云进等[19]发现,随着分离时间的延长和温度的升高,油浆分离效率提高;郭爱军等[20-21]发现,某些添加剂会促进FCC油浆中催化剂颗粒的团聚,提高静电分离效率。物性参数方面,方云进等[19]设计了静电分离装置,考察油浆黏度和填料材料等对静电分离效率的影响,发现分离效率随着油浆黏度减小而提高,且以玻璃珠为床层介质时分离效率更好;Bose等[22]发现,在实验前使用电极震荡方式对油浆进行降黏处理,可提高催化剂的分离效率。
由上述可知,目前的研究主要分析了FCC油浆在静态流场中静电分离影响因素,而对其在动态流场中的静电分离规律缺少探讨。有限元分析是利用数学近似的方法对真实的物理工况进行模拟的一种方法,适用于对FCC油浆的静电分离模拟。因此,笔者基于有限元分析软件COMSOL,建立了静电分离场的三维数值模型,模拟静止流场和运动流场的电场分布、颗粒运动轨迹,分析不同流态下颗粒的受力情况与其速度的变化,并通过改变电压以及流速来研究不同工况下催化剂颗粒的分离效率,以优化FCC油浆静电分离的效率。
1 颗粒受力分析与模型构建
1.1 颗粒受力分析
FCC油浆的静电分离过程是在电场、流场和重力场的耦合作用下进行的,催化剂颗粒在FCC油浆中受到介电泳力、曳力和重力的作用而被吸附到填料球表面,其中介电泳力是颗粒运动的主要驱动力。当电介质颗粒位于介电液体中时,在非均匀电场的作用下,固相颗粒会被极化成1个偶极子。这是因为电场不均匀时,电场内不同位置处的极化电荷受到的电场力不同,不同极化电荷受到的电场力的矢量叠加,固体颗粒表面宏观上表现为受到1个净力,即为介电泳力。该理论首先由Phol于1951年提出[23],颗粒所受介电泳力(FDEP,N)表达式如式(1)所示。
(1)
式中:dp表示固相颗粒的直径,mm;ε0表示绝对介电常数,为8.85×10-12F/m;εr,f和εr,p分别表示油浆和催化剂颗粒的相对介电常数,无量纲;E表示电场强度值,V/m。颗粒在油浆中所受有效重力(FEG,N)由式(2)计算[24]。
(2)
式中:ρp表示20 ℃时颗粒密度,kg/m3;g表示重力加速度。颗粒所受曳力(FSD,N)如式(3)所示。
(3)
式中:up和uf分别表示颗粒和油浆的速度,m/s;τp表示颗粒速度的响应时间,s;当雷诺数较低且位于斯托克斯区时,τp=ρpdp2/18μ,代入式(3)可得[15]:
FSD=-3πμdp(up-uf)
(4)
式中:μ表示20 ℃时油浆动力黏度,Pa·s。
1.2 模型构建
研究以径向型静电分离器为对象,该分离器由2个同轴心内外电极板组成,2个电极板之间的区域填充满玻璃球,作为填料对催化裂化油浆中的催化剂颗粒进行吸附。本研究以六方堆积的填料排列方式[25]为分离单元进行建模,模型内、外表面分别为内、外电极,其中内电极直径为10 cm,外电极直径为21.5 cm,填料球直径为3 mm,三维数值仿真模型如图1所示。模型的内电极连接电源正极,电压为U0;外电极接地,电压U’=0;其余边界均为绝缘界面,电荷Q=0。
采用COMSOL数值仿真软件对FCC油浆静电分离进行模拟,计算过程分2个步骤:第一,选取静电(es)模块求解几何模型中的电场,基于电场的强度和方向不变,采用稳态求解方法得到计算域中的电场分布;第二,基于电场的求解结果,选取软件中流体粒子追踪(fpt)模块,采用瞬态求解方法对整个计算域内的颗粒运动进行求解,得到颗粒的运动轨迹。

Q—Electric charge;U0—Internal electrode voltage;U’—External electrode voltage图1 径向型静电分离器几何模型及边界条件示意图Fig.1 Schematic diagram of geometric model and boundary conditions
(1)电场控制方程
静电分离器计算域内各位置的电场强度(E)[15]可由式(5)来求解。
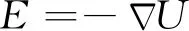
(5)
式中:U为电势,V。根据高斯定律,静电场中任意闭合曲面内电位移通量的积分为该闭合曲面内电荷的总量,如式(6)所示[26]。
(6)
式中:ρqv为单位体积电荷密度,C/m3。εr为相对介电常数,当计算域是颗粒时取εr,p,当计算域是油浆时取εr,f。利用式(5)和式(6)可以计算出计算域内的电场分布。
(2)流场控制方程
利用式(1)、式(2)和式(3)通过牛顿第二定律求解流场中颗粒运动状态,如式(7)所示[15]。
(7)
2 静电分离器内电场特性分析
静电分离器几何模型电势分布如图2(a)所示;其xz横截面上的电场强度云图如图2(b)所示。由图2(a)可知:其内电极施加10 kV直流电压,即U0=10000 V;外电极接地;电势由内电极至外电极逐渐减小。由图2(b)可知,填料球与内电极接触点处电场强度最大,距离外电极越近,电场强度越小。
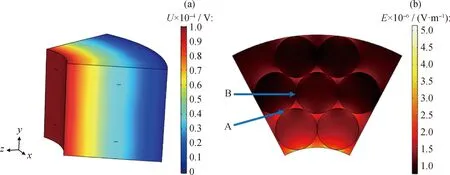
A,B—Test pointsU—Electric potential;E—Electric field intensity图2 模型电势与横截面电场强度分布Fig.2 Model electric potential and cross-sectional electric field intensity distribution(a)Electric potential;(b)Electric field intensity
李强等[15]提出了“有效接触点”模型,并利用该模型研究了填料排列方向与外加电场之间所成夹角θ的大小对颗粒吸附的影响。模型表达式如式(8)所示。
(8)
式中:a为修正因子;εr,g表示填料球的相对介电常数,无量纲;r为颗粒接触点在静电分离器内的径向位置,mm;Rin和Rout分别为静电分离器的内外电极的半径,mm。
研究结果表明:当θ在0°~80°时,由填料极化产生的退极化场与原电场方向相同,对原电场有增强作用,因而填料接触点区域场强增大,对颗粒的吸附能力增强;当θ在80°~90°时,填料极化产生的退极化场与原电场方向相反,对原电场有削弱作用。以图2(b)中的A、B两点为例,施加在模型上的原电场场强为1.35×106V/m,A点的夹角θA在0°~80°,其场强为2.65×106V/m,较原电场增大;B点夹角θB在80°~90°,其场强为9.98×105V/m,较原电场减小。
3 不同流场中颗粒运动分析
3.1 静止流场中颗粒运动分析
3.1.1 静止流场中颗粒运动轨迹
利用激光粒度仪测得催化剂颗粒的粒径分布如图3所示。由图3可知,催化剂粒径中位数约为3 μm,因此模拟中设置催化剂的粒径为3 μm。在求解域中均匀释放378个固体颗粒,颗粒在介电泳力、重力和曳力的共同作用下发生运动,模拟时间10 min,颗粒的运动轨迹和最终吸附位置如图4(a)所示。而图4(b)为相同条件下实验时,在显微镜下观察到催化剂颗粒的最终静电吸附位置。从图4可以看到,填料接触点周围是颗粒吸附的主要位置,由红框标示。这是因为,玻璃珠填料在外加电场中通过极化使接触点处的电场强度增大(图2(b)),催化剂颗粒在介电泳力的作用下向高电场强度方向运动,进而在填料接触点周围大量聚集并吸附到填料表面。
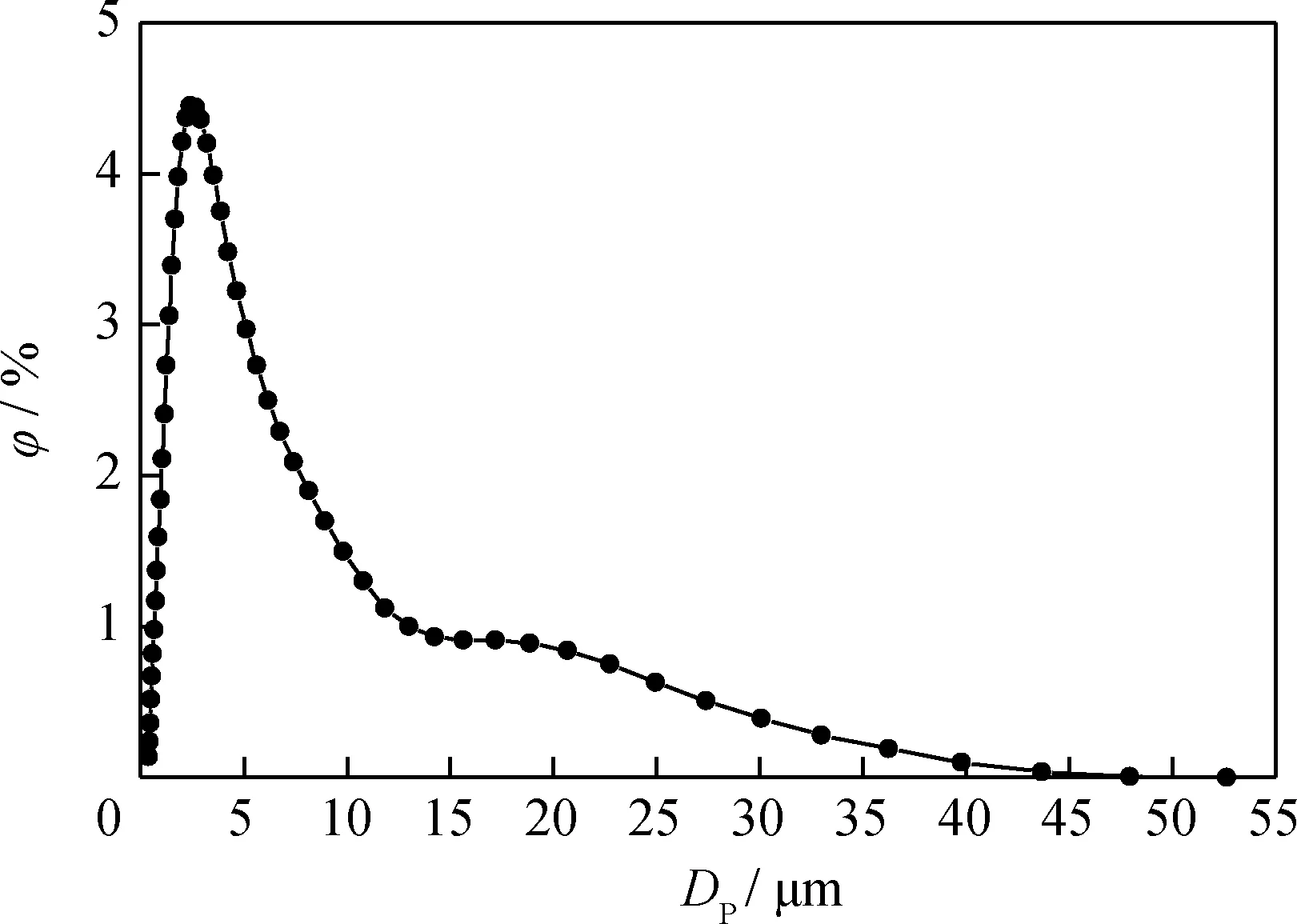
φ—Volume;Dp—Particle diameter图3 催化剂颗粒粒径分布图Fig.3 Catalyst particle size distribution diagram
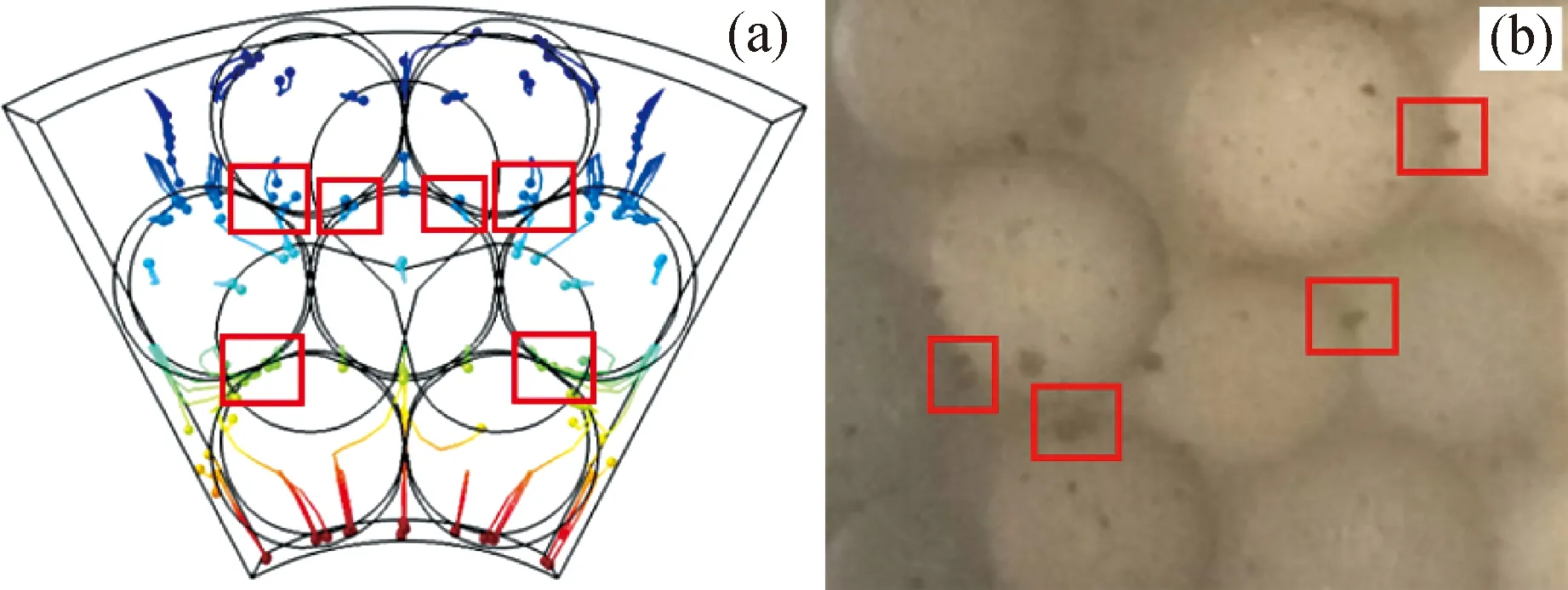
图4 模拟和实验中颗粒最终吸附位置Fig.4 Final adsorption position of particlesbased on simulation and experiment(a)Simulation;(b)Experiment
3.1.2 静止流场中颗粒受力和速度分析
在x轴和z轴方向,颗粒受到介电泳力和曳力的作用,而静止流场中油浆速度为0,即uf=0,因此由式(1)和式(4)可求得x轴和z轴方向上颗粒的速度upn为:
(9)
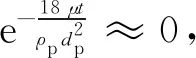
(10)
(11)
式(11)中:当介电泳力和重力方向相同时取负号,当方向相反时取正号;式中第二项是由重力产生的定量项,因此y轴方向颗粒速度与其受到的介电泳力不成正比例关系。但在x、y、z轴3个方向上,颗粒速度与介电泳力均成正相关变化。
取单个颗粒模拟分析在多场耦合作用下颗粒的受力情况和速度大小,颗粒释放三维坐标位置为(0.0035,0.00245,0.0005),运行10 min后,颗粒在各方向的速度与介电泳力关系如图5所示。由图5可知:在x轴方向和z轴方向上,任一时刻颗粒的速度与其受的介电泳力都成正比例关系;并且,在3个方向上,颗粒速度与其受的介电泳力成正相关变化,与式(10)和式(11)一致。
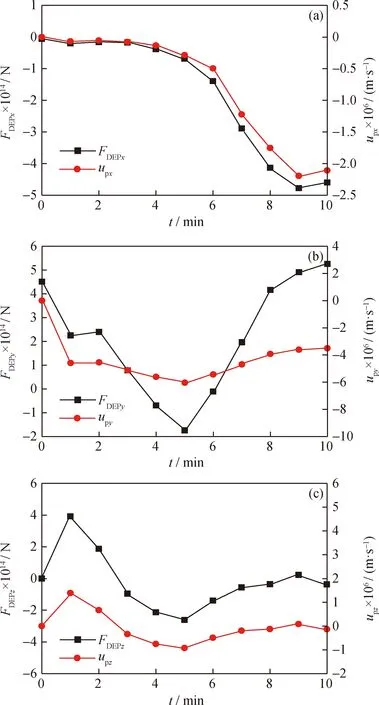
FDEPx—Dielectrophoretic force in the x-axis direction;FDEPy—Dielectrophoretic force in the y-axis direction;FDEPz—Dielectrophoretic force in the z-axis direction;uPx—Particle velocity in the x-axis direction;uPy—Particle velocity in the y-axis direction;uPz—Particle velocity in the z-axis direction;t—Simulation time图5 静止流场中颗粒速度(up)与介电泳力(FDEP)关系Fig.5 Relationship between particle velocity (up)and dielectrophoresis force (FDEP)in static flow field(a)x axis direction;(b)y axis direction;(c)z axis direction
将式(10)和式(11)分别带入式(4)中,可进一步得到颗粒在x(或z)轴和y轴方向上所受曳力表达式,如式(12)和式(13)所示。
(12)
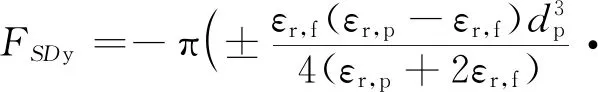
(13)
由式(12)~(13)可知,在x轴方向和z轴方向上,颗粒所受曳力大小与其所受介电泳力大小成正比例关系,而在y轴方向上二者不成正比例关系。在x、y、z轴3个方向上,颗粒所受曳力大小随介电泳力成正相关变化。将单颗粒模拟得到的颗粒在各方向所受曳力和介电泳力进行对比,如图6所示。由图6 可知,颗粒所受曳力的变化趋势与式(12)和式(13)描述相符合。
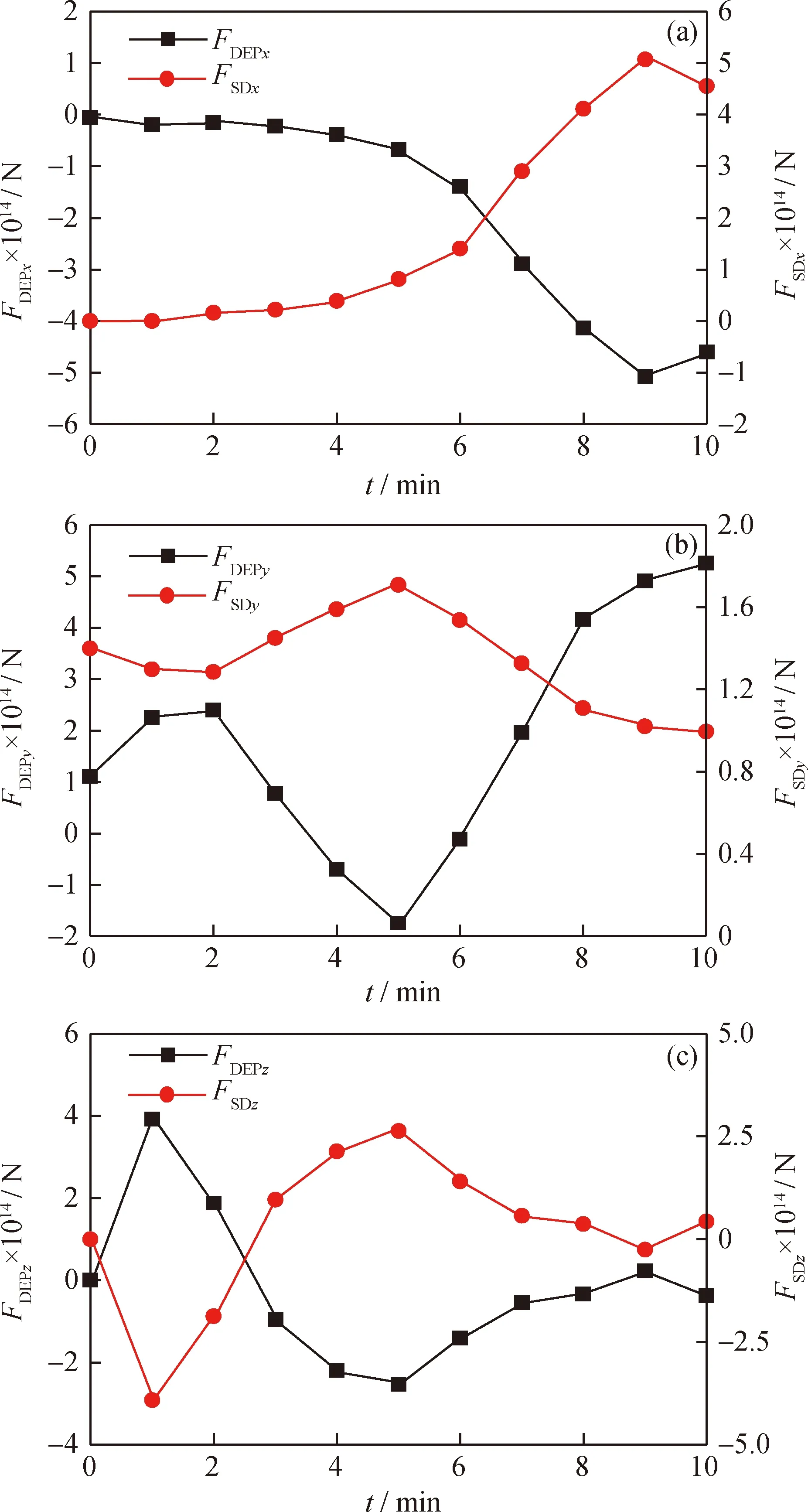
FDEPx—Dielectrophoretic force in the x-axis direction;FDEPy—Dielectrophoretic force in the y-axis direction;FDEPz—Dielectrophoretic force in the z-axis direction;FSDx—Drag force in the x-axis direction;FSDy—Drag force in the y-axis direction;FSDz—Drag force in the z-axis direction;t—Simulation time图6 静止流场中颗粒各方向曳力(FSD)和介电泳力(FDEP)大小Fig.6 Drag force (FSD)and dielectrophoresis force (FDEP)of particles in each direction in the static flow field(a)x axis direction;(b)y axis direction;(c)z axis direction
3.2 重力方向运动流场中颗粒运动分析
3.2.1 重力方向运动流场中颗粒运动轨迹
油浆由模型上入口流入,下出口流出称为“重力方向运动流场”。运动流场通过在静止流场基础上添加层流模型进行模拟,设置重力方向流场入口油浆速度uf为0.0001 m/s,出口压力p设为0 Pa,释放固体颗粒数N为378,模拟运行时间t为10 min。颗粒运动轨迹及其在z=0处xy平面上的运动示意如图7所示,图中背景颜色表示油浆速度,箭头表示颗粒运动方向。由图7可知:重力方向流场中只有24个颗粒被吸附到玻璃珠填料上,大部分颗粒在下出口流出;填料接触点处油浆流速较小,而填料之间空隙处油浆流速较大,因此大部分催化剂颗粒在油浆的带动下通过填料间隙流出,而不能被有效吸附。
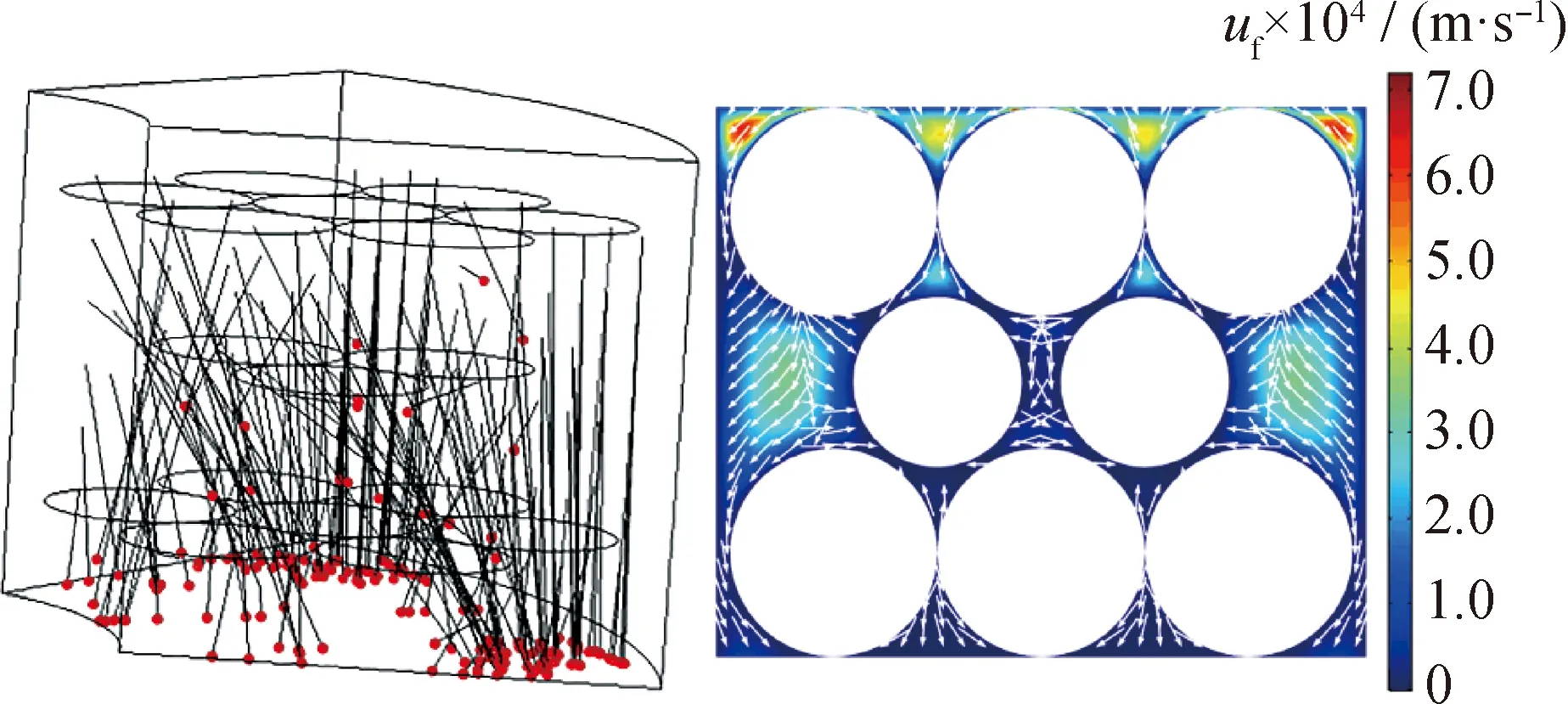
图7 重力方向运动流场中颗粒运动轨迹及其在z=0截面上速度及运动方向示意Fig.7 Particle trajectory diagram in the flow field of gravity direction movement and their velocitiesSimulating conditions:Direction on z=0 section;uf(Inlet)=0.0001 m/s;p=0 Pa;N=378;t=10 min uf—Slurry velocity
3.2.2 重力方向运动流场中颗粒受力和速度分析
取单个粒子并在三维坐标(0.0035,0.00245,0.0005)处释放,模拟运行10 min,得到颗粒受力关系如图8所示。由图8可知:在模拟2 min后,颗粒受力不再变化,表示颗粒已被吸附到填料球表面;颗粒所受的曳力比介电泳力大4个数量级,比重力大3个数量级,曳力较大造成了大部分催化剂颗粒在运动油浆的带动下通过填料间隙而不能被填料有效吸附。
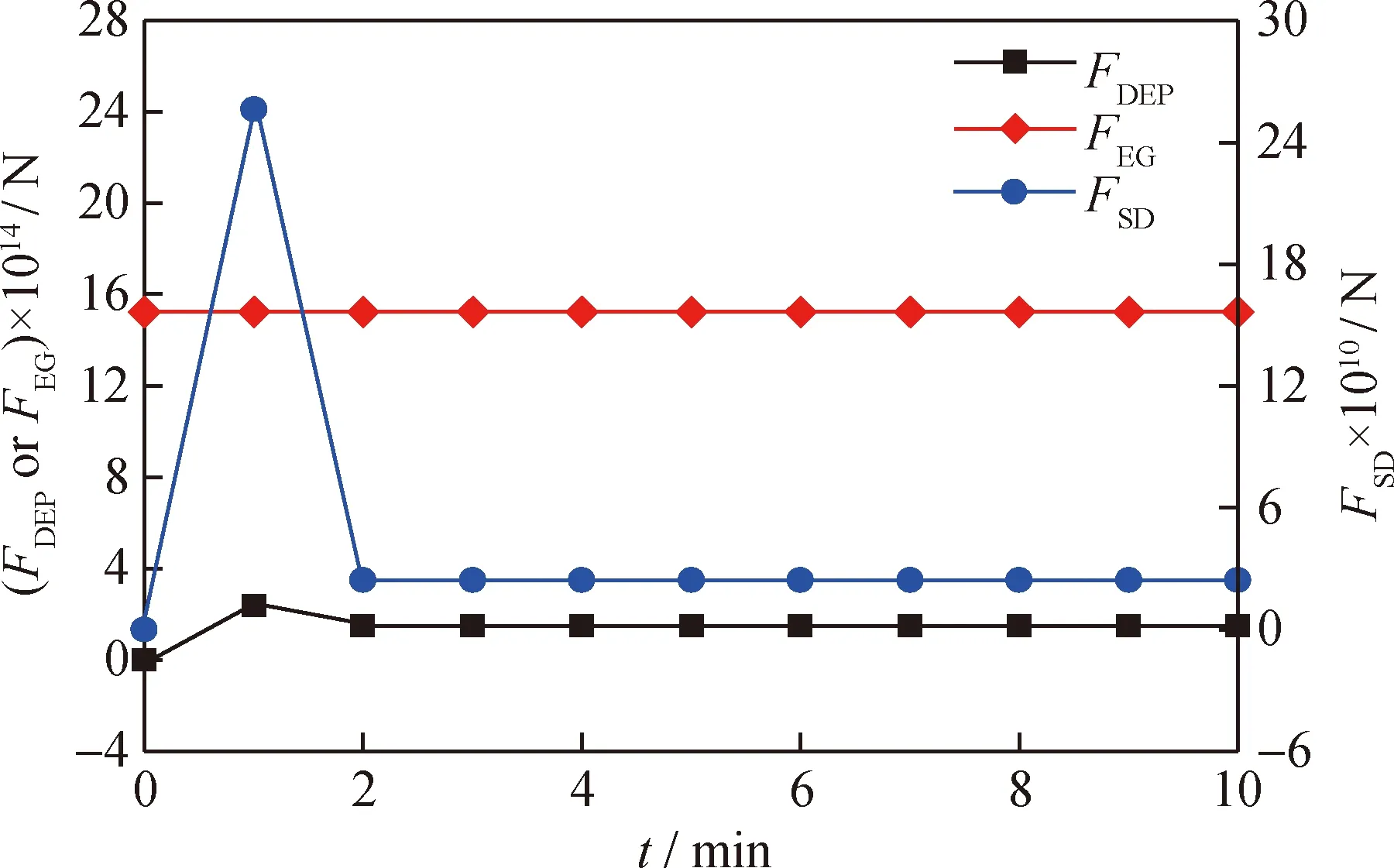
FDEP—Dielectrophoretic force;FEG—Effective gravity;FSD—Drag force;t—Simulation time图8 重力方向运动流场中颗粒受力大小Fig.8 Force of particles in the flow field moving in the direction of gravity
在x轴方向和z轴方向,颗粒受到介电泳力和曳力的作用,而运动流场中油浆速度不为0,即uf≠0,因此由式(1)和式(4)可求得x轴方向和z轴方向上颗粒速度如式(14)所示。
(14)
在y方向因受到重力作用,颗粒的速度如式(15)所示。
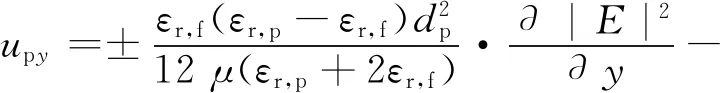
(15)
由于运动流场中油浆流速的不确定性,因而颗粒在3个方向上的速度也不能确定。因此,颗粒所受介电泳力与颗粒速度无相关关系,不能用介电泳力定性分析颗粒的速度。
3.3 逆重力方向运动流场中颗粒运动分析
3.3.1 逆重力方向运动流场中颗粒运动轨迹
油浆由模型下入口流入,上出口流出称为“逆重力方向运动流场”。与重力方向运动流场相同,设置入口油浆流速uf为0.0001 m/s,出口压力p为0 Pa,释放固体颗粒数N为378并设置模拟运行t为10 min。颗粒运动轨迹及其在z=0处xy平面上的运动示意如图9所示。由图9可知:只有25个颗粒被吸附到玻璃珠填料上,大部分颗粒从上出口流出;同重力方向运动流场相似,填料球之间空隙内油浆流速大于其在填料球接触点处流速,多数催化剂颗粒被油浆带动从上出口流出。

uf—Slurry velocity图9 逆重力方向运动流场中颗粒运动轨迹及其在z=0截面上速度及运动方向示意Fig.9 Particle trajectory diagram in the flow field moving against gravity and their velocitiesSimulating conditions:Direction on z=0 section;uf(Inlet)=0.0001 m/s;p=0 Pa;N=378;t=10 min
3.3.2 逆重力方向运动流场中颗粒受力和速度分析
取单个粒子在三维坐标(0.0035,0.00245,0.0005)处释放,模拟运行10 min,得到颗粒受力关系如图10所示。由图10可知:与重力方向运动流场相同,颗粒在2 min时被吸附到填料球表面;颗粒所受的曳力比介电泳力大4个数量级,比重力大3个数量级;同样,由于颗粒所受曳力较大,其不容易被吸附到填料球表面。
在逆重力方向运动流场中,颗粒在x轴方向和z轴方向上只受介电泳力和曳力作用,因此其速度表达式与重力方向运动流场相同(式(14));而在y轴方向上,颗粒所受的曳力方向与重力运动流场相反,因此颗粒y轴方向速度如式(16)。
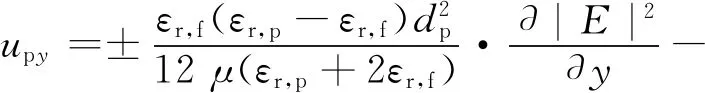
(16)
与重力方向运动流场中相同,在逆重力方向运动流场中,由于颗粒速度的不确定性,不能用介电泳力对颗粒速度进行定性分析。
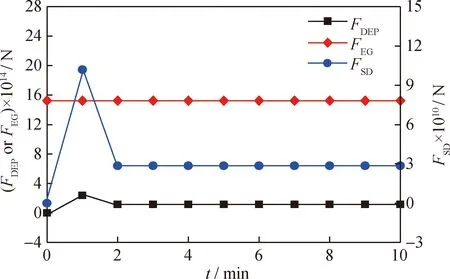
FDEP—Dielectrophoretic force;FEG—Effective gravity;FSD—Drag force;t—Simulation time图10 逆重力方向运动流场中颗粒受力大小Fig.10 Force of particles in flow field moving against gravity
4 操作参数对分离效率的影响
将计算域中释放的颗粒总数记为N;模拟10 min 后,将被吸附到填料表面的颗粒总数记为N’。因此,模型中颗粒静电分离效率η计算公式见式(17)。
(17)
模拟分析电压变化对分离效率的影响,施加在正极的电压变化范围为6000~14000 V,间隔为2000 V,运动流场的入口油浆流速均设置为0.0001 m/s,模拟时间为10 min,各流场中颗粒分离效率如图11所示。由图11可知,随着施加电压由6000V增大到14000V,静止流场分离效率(ηs,%)提高7.14百分点,运动流场(重力或逆重力方向)分离效率(ηm,%)分别提高5.82(重力方向)和5.96(逆重力方向)百分点。相比运动流场中颗粒所受曳力较大的情况,静止流场中颗粒流速为0,颗粒所受曳力较小,因此相同电压下静止流场中颗粒分离效率较大;相同电压下,逆重力方向运动流场的颗粒分离效率大于重力方向运动流场的。
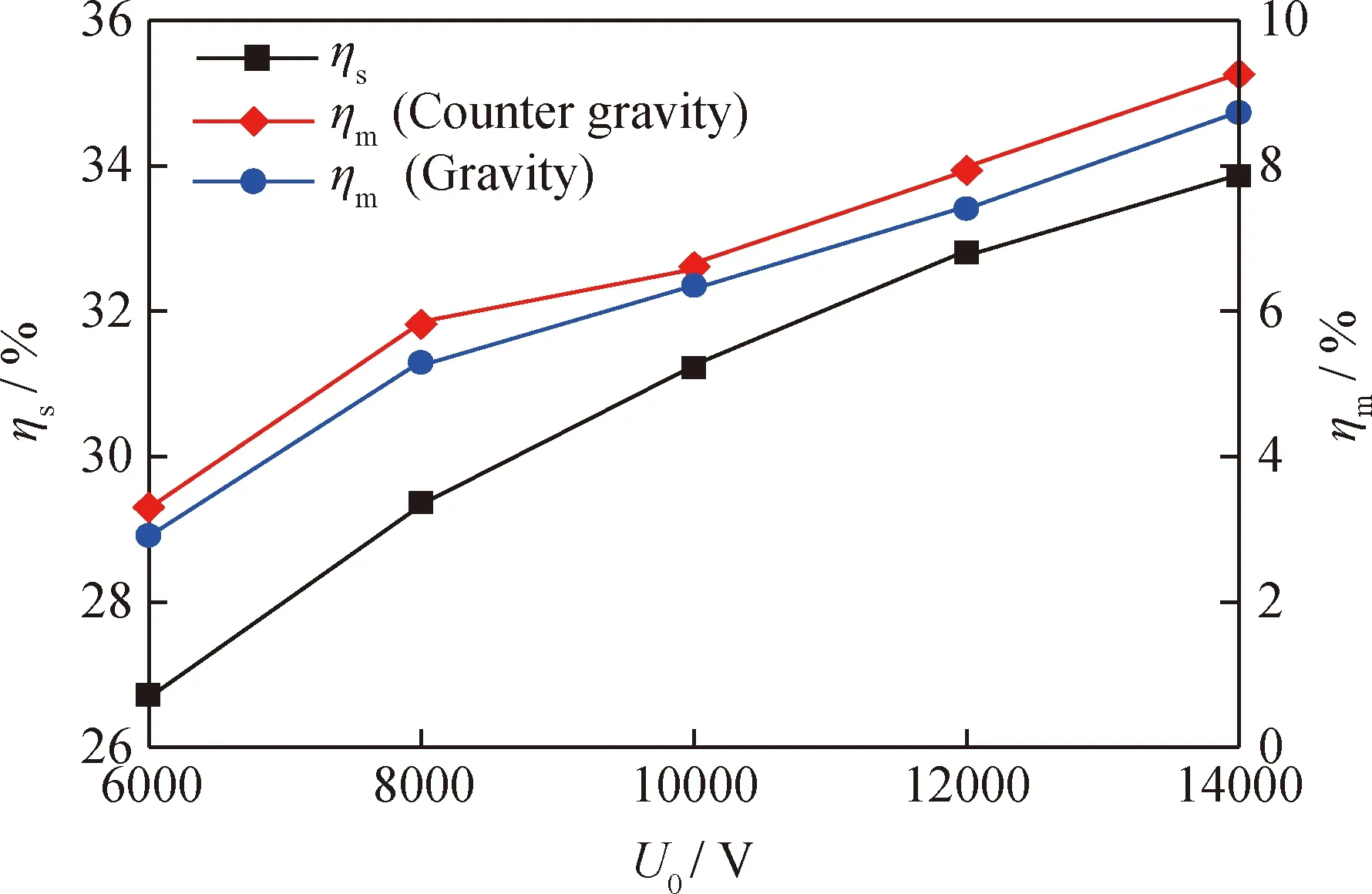
ηs—Separation efficiency in static flow field;ηm—Separation efficiency in moving flow field;U0—Internal electrode voltage图11 各流场中颗粒分离效率(ηs)与电压(U0)关系Fig.11 Relationship of particle separation efficiency (ηs) with voltage (U0)in different flow fields
油浆速度对运动流场中颗粒的吸附效率具有重要影响,取流场入口油浆速度0.0001~0.001 m/s,间隔0.00025 m/s,2种运动流场中颗粒分离效率如图12所示。从图12可知,随着入口油浆速度的增大,颗粒分离效率逐渐降低,原因是颗粒所受曳力随油浆流速增大而增大。在同一流速下,重力方向运动流场中颗粒分离效率高于逆重力方向运动流场,是因颗粒在逆重力方向运动流场中所受的曳力要小于其在重力方向运动流场中所受的曳力。同时,颗粒在运动流场中所受的曳力远大于其所受的重力和介电泳力,使其运动流场中的分离效率小于静止流场中的。
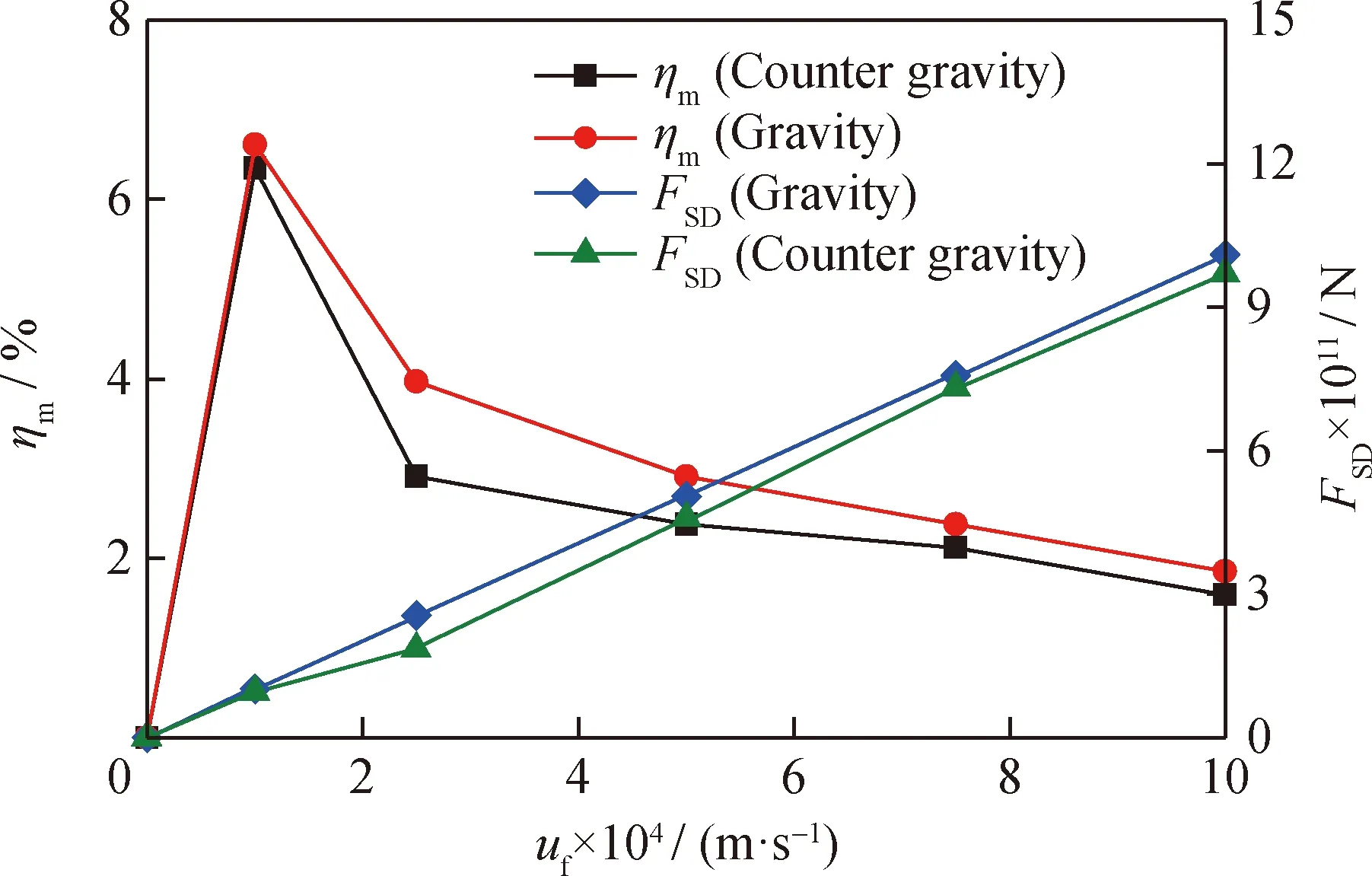
ηm—Separation efficiency in moving flow field;FSD—Drag force;uf—Slurry velocity图12 运动流场中颗粒分离效率(ηm)和所受曳力(FSD)随流速(uf)的变化规律Fig.12 Variation of particle separation efficiency (ηm)and drag force (FSD)with velocity (uf)in moving flow field
5 结 论
(1)由于填料球在电场中受到极化的作用,一定排列角度范围内的填料球接触点处电场强度增大,是静电分离器内静电吸附催化剂颗粒的主要位置。
(2)在静止流场的x轴和z轴方向,颗粒所受介电泳力和曳力成正比例关系,颗粒运动速度与所受介电泳力也成正比例关系;而在y轴方向,其并非正比例关系;但在3个方向上,颗粒速度与介电泳力、颗粒所受曳力与介电泳力均成正相关变化。而在运动流场中,由于颗粒在各位置速度具有不确定性,颗粒速度与其受力间不存在相关关系。
(3)与静止流场相比,颗粒在运动流场中所受曳力更大,导致运动流场中的颗粒分离效率低于静止流场中的。颗粒在逆重力方向运动流场中所受曳力小于其在重力方向运动流场中的,因此其在前者中的分离效率高于后者。随施加电压增大,各流场中颗粒分离效率提高;相同电压下,逆重力方向运动流场中颗粒分离效率大于重力方向运动流场中的。运动流场中,颗粒分离效率随入口油浆流速增大而降低;相同流速下,重力方向运动流场中颗粒分离效率大于逆重力方向运动流场中的。

