基于傅里叶描述子和共振频率的不规则果形梨果硬度评估指标构建

王 鹏 ，吴 杰 ,2※

（1.石河子大学机械电气工程学院，石河子 832000；2.绿洲特色经济作物生产机械化教育部工程研究中心，石河子 832003）

0 引 言

果蔬硬度是其重要的内部品质之一，硬度与果蔬的口感、成熟度等密切相关，是梨果品质检测重要指标。国内外学者研究发现共振频率是评估硬度变化的重要参数。通常果蔬硬度采用频率指标f2m2/3（f为赤道部感测频率，m为质量）评价[1]，但已有研究表明，果形对果蔬共振频率有影响，Chen等[2]研究指出，评价指标f2m2/3适于近球形果蔬的硬度评价，但对非球形果蔬硬度评价误差较大。为此，Cherng等[3]提出了一种适于评价椭球形果蔬硬度的双频指标SCherng=()2/3m2/3ρ1/3（f1为赤道部感测频率，f2为萼端或梗端感测频率，ρ为果蔬密度），笔者团队针对多为卵圆形的库尔勒香梨，从香梨赤道部和萼端分别感测共振频率f1和f2，构建了一种双频硬度指标Sf1f2= ( 0.4f1+ 0.6f2)2m2/3，提高了香梨硬度评价性能[4]。尽管如此，梨果种类丰富，果形复杂，其中啤梨为典型的果形不规则梨果，现有的各种基于规则果形构建的频率指标，可能都不适于啤梨硬度的精确评价。因此，有必要基于共振频率构建一种适于评价果形不规则梨果硬度的指标。

针对复杂果形果蔬，了解果形对共振频率的影响规律，是构建消除果形影响的新硬度评价指标的关键。大多研究采用纵横比、圆度比、圆形度、偏心度、离心率等描述果形[5-9]，李凡等[5]采用纵横比和圆度比对香梨形状定量描述获得5种果形，申翠香等[7]采用圆形度描述苹果果形。这些描述方法多用于苹果、桃子、柑橘等“比较端正”果形的描述[8-11]，但却很难全面描述果形复杂不规则的梨果。近年来，郝敏等[12]采用具有平移伸缩和旋转不变性且有多特征描述能力的Zernike矩描述马铃薯，但Zernike矩描述果形时，数据处理量大，计算耗时长[13]。傅立叶描述子具有很强的果蔬外形重建功能且对复杂果形有较强的描述能力[14-16]，这一方法在描述木瓜、畸形马铃薯、杨桃等果蔬外形轮廓时，能够兼顾全局及局部特征[17-19]，其中 Limsiroratana等[17]研究木瓜果形描述方法时，发现傅里叶描述子计算快速且抗噪性强；EIMasry等[18]采用傅里叶描述子描述畸形马铃薯，并选取4个傅里叶描述子识别畸形马铃薯，识别率可达 96.2%；Abdullah等[19]采用傅里叶描述子描述杨桃外形，对3种变形果的识别率最高可达 100%。上述研究表明傅里叶描述子可以描述果形复杂多变的果蔬外形特征。

因此，本文采用傅里叶描述子对啤梨果形进行定量描述，并结合试验模态和有限元模态分析方法，了解啤梨果形变化对其频率的影响规律，构建适于不规则果形的梨果硬度准确评价指标，为复杂果形梨果硬度振动法无损检测提供研究基础。

1 材料与方法

1.1 啤梨试样

啤梨试样于2019年10月于石河子水果批发市场采购，剔除损伤及病虫害试样，立即贮藏于−2～0 ℃、相对湿度85%～95%的冷库备用。试验前将试样在(23±1)℃室温下回温24 h。

1.2 研究思路

首先结合试验模态和有限元模态分析结果确定啤梨试样适宜的振型和对应的模态频率，采用傅里叶描述子和纵横比描述啤梨试样果形；然后利用Pearson线性相关性分析果形对啤梨振动频率的影响规律，进而构建含有果形描述子和共振频率的新硬度评估指标以消除果形对硬度评估的影响；最后结合M-T穿刺硬度实测值，采用普通最小二乘法（ordinary least square, OLS）分别对基于频率的无损硬度与M-T穿刺硬度SMT进行线性回归分析。研究方案流程如图1所示。

1.3 啤梨试验模态分析

试验模态分析系统如图2所示，选择单点感测多点激励方式采集振动信号构建频率响应函数[4]，啤梨试样用橡皮筋悬挂使其处于接近自由振动状态。根据前期试验在试样表面均布56个点，取赤道部的32号点（见图3）为感测点，LC1305型力锤（河北朗斯有限责任公司）以9～12 N的力从1号点依次开始敲击各点[4]，固结在感测点的LC0408T型加速度传感器（河北朗斯有限责任公司）感测信号，随机选取10个试样进行试验模态分析。

1.4 啤梨有限元模态分析

如图4所示，采用Rigelscan Elite型三维扫描仪（精度0.0185 mm，武汉中观自动化科技有限公司）获得啤梨试样.asc格式点云模型，然后将其导入正逆向混合设计软件Geomagic Wrap 2017（美国，Geomagic公司）进行逆向处理，获得.stp格式实体模型，最后将实体模型导入有限元分析软件Abaqus 2017（法国，达索SIMULIA公司）中进行有限元分析。

采用有限元软件Abaqus 2017（法国，达索SIMULIA公司）划分网格时，由于啤梨试样小且形状不规则，因此选用10节点二次四面体结构实体单元C3D10进行自由网格划分，避免大量分割操作导致工作量增加和人为误差。为减少计算时间，在保证精度的前提下将网格大小设定为2 mm。假设啤梨为均质、各向同性的线弹性体，模型泊松比取0.3[20]，采用排水法测得啤梨密度。采用有限元分析软件 Abaqus进行啤梨有限元模态分析时，在Frequency分析步中选择子空间迭代算法（subspace）求解器，求解运动方程+Ka(t) = 0（M为质量矩阵，为加速度矢量，K为刚度矩阵，a(t)为速度矢量），设置最大频率为1 000 Hz，频移为100 Hz，特征值提取数量为20，每次循环矢量数为28次，最大循环次数为30次，获得啤梨前20阶模态振型和对应的固有频率进行分析。

1.5 啤梨固有频率归一化

由于质量对模态固有频率影响很大[21-22]，采用模态分析啤梨果形对频率影响时，用式（1）对各阶模态固有频率进行归一化处理以消除质量对固有频率的影响[20]：

式中m为试样质量，kg；m0为常数，根据前期试验取0.1 kg；f为某一阶模态固有频率，Hz；fn为归一化的固有频率，Hz。

1.6 啤梨果形描述方法

1.6.1 果形轮廓的提取

采用EOS 750D型佳能数码相机（日本，佳能有限公司）采集啤梨图像，采用Matlab 2014（美国，MathWorks公司）软件中图像处理工具箱对啤梨图像进行灰度变换、阈值分割、边界提取，获得试样外形轮廓，如图5所示。

1.6.2 试样轮廓半径序列的计算

如图6，计算试样轮廓曲线的形心坐标x0和y0[23]：

式中n为试样边界轮廓曲线上的总样点数；k为边界轮廓曲线上点的序数。求得形心坐标x0和y0后，以形心坐标为圆心，果梗与果体交界处P1点作为起始点，按逆时针方向求半径序列r(k)：

1.6.3 半径序列的傅里叶变换

为避免试样大小对果形分析的影响，将半径序列r(k)归一化处理[24]：

式中rav为试样的平均半径，Pixels；n为试样边界轮廓的样点数，rg(k)为归一化半径序列。对归一化半径序列rg(k)进行离散傅里叶变换：

式中Fh为傅里叶描述子，h为傅里叶变换后的自变量，2π/n为相邻两样点间夹角，Fh可理解为半径序列变化h次的程度[23]。当h=0时，F0表征试样平均半径信息，F1表征试样外形的弯曲程度信息，F2表征试样外形的伸长度信息，F3表征试样外形的三角度信息，F4表征试样外形的方形度信息[24]。

1.6.4 纵横比q的计算

采用纵横比描述啤梨果形时，测量如图7所示啤梨试样肩高的最大值Hmax(mm)和最小值Mmin(mm)以及赤道部最大直径Dmax(mm)和最小直径Dmin(mm)，纵横比q由公式（9）计算求得[4]。

1.7 啤梨硬度的M-T穿刺法测定

采用TA.XP plus质构仪（英国，Stable Micro System公司）在啤梨梗端、赤道部和萼端 3个区域内每个区域随机选取4个点进行带皮M-T穿刺试验[25-26]。采用直径5 mm 的圆柱探头，穿刺速度为 1 mm/s，穿刺深度为8 mm。穿刺硬度由穿刺前曲线的斜率计算得出，然后取12次穿刺试验平均值作为梨整体硬度。

1.8 硬度评估指标的评价方法

在室温(23±1) ℃、相对湿度 20%环境下，随机选取140个啤梨试样等分为7组，每2 d进行一次测试试验。试验时随机选取一组啤梨试样，每个试样在15 min内依次进行激振试验、图像采集和M-T穿刺试验，获得啤梨基于频率的无损硬度和M-T穿刺硬度。

采用普通最小二乘法（Ordinary Least Square, OLS）分别对基于频率的无损硬度与M-T穿刺硬度SMT（N/mm）进行线性回归分析[26]，回归方程为

式中SZ为各频率指标中的某一个；α和β分别为回归方程的回归系数和截距。

2 结果与分析

2.1 试验模态对有限元模态的验证

2.1.1 试验模态与有限元模态的分析结果

瑞士有很多传统的奶酪饮食，其中奶酪火锅就是其中最著名的一款。如果说瑞士有什么美食的话，那一定首推奶酪火锅。瑞士盛产奶酪，而且法令规定一个地区只能生产该地区产的奶酪，因此瑞士的奶酪直至今日仍能够保持极其传统的风味，且不同地区的奶酪味道各不相同。

通过啤梨试验模态分析获得 3个模态，分别为弯曲模态、挤压模态和呼吸模态，如图8所示。可以看到，弯曲模态在啤梨梗端发生较大变形，在萼端几乎不发生振动变形；挤压模态在赤道部发生最大变形，呼吸模态主要沿啤梨径向发生扩张和收缩的振动变形。

啤梨进行有限元模态分析所获得的20阶有限元模态振型中，第1～6阶频率近似为0，为刚体模态；第16～20阶振型变形复杂，为二阶模态，本研究不予考虑。在第7～15阶振型中，第8阶与第7阶变形相同，均为弯曲模态，第10阶为挤压模态，第13～15阶模态变形相同，均为呼吸模态。

2.1.2 试验模态与有限元模态频率对比

调整有限元分析弹性模量值，当第 7阶有限元弯曲模态频率与试验模态结果相同时，确定弹性模量值Eest，取这一弹性模量值为有限元模态分析的弹性模量并计算剩余各阶有限元模态的固有频率值[4]。计算有限元模态频率与试验模态频率的差值，以差值绝对值与试验模态频率比值大小判别有限元模态分析的准确性。任取10个啤梨试样进行试验，结果如表1所示。频率的有限元结果与试验结果的相对误差不超过3.25%,表明采用各向同质线弹性体的梨实体建模进行有限元模拟结果较准确，因此可以采用有限元模态分析果形对频率的影响规律。

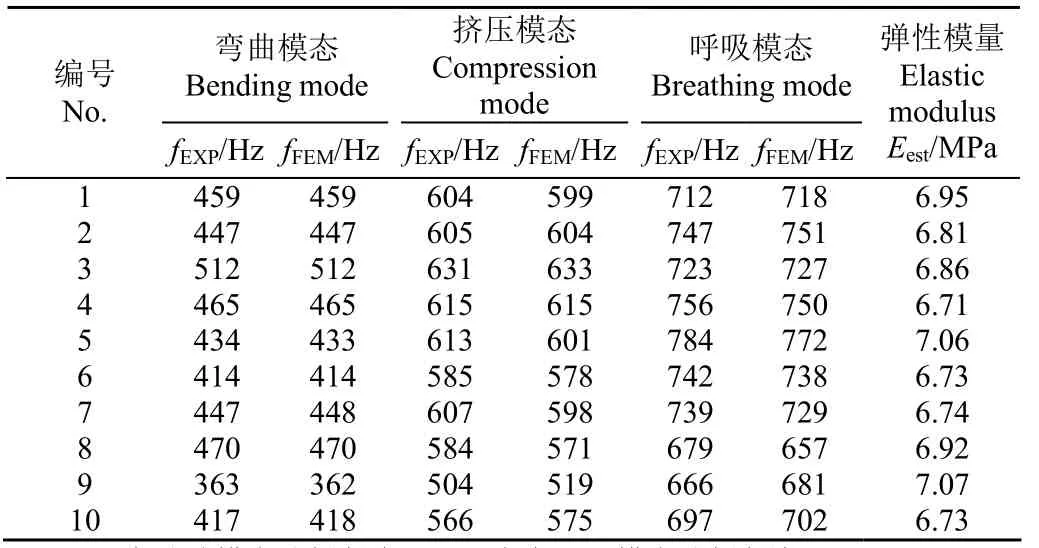
表1 试验模态分析与有限元模态分析频率比较Table 1 Comparisons between the experimental frequencies and the FEM frequencies

2.2 傅里叶描述子对啤梨外形描述结果分析

如图9所示，前20个傅里叶描述子与F0的比值随h增大迅速减小，但F4和F6与F0的比值出现反弹。当h大于16时，Fh与F0比值曲线趋于水平且比值小于0.005，即啤梨果形信息主要集中在前16个傅里叶描述子。

梨试样轮廓和前10、15、20个傅里叶描述子反变换图如图10所示，采用前10个傅里叶描述子反变换获得的梨轮廓图基本能描述梨果形，但对啤梨梗端或萼端轮廓重合度较差；采用前15个傅里叶描述子反变换获得的轮廓与原轮廓形状度吻合度高。因此，尽管采用前20个傅里叶描述子反变换获得的轮廓仍然与梨轮廓保持很好重合度，但采用前15个傅里叶描述子已足以描述啤梨试样轮廓的主要信息。

2.3 果形对啤梨共振频率的影响

对 100个啤梨进行有限元模态分析，本研究取弯曲模态、呼吸模态和挤压模态的归一化固有频率进行分析。采用Pearson相关性分析方法对啤梨弯曲、呼吸和挤压3种模态的归一化固有频率和前15个傅里叶描述子进行线性相关性分析，与归一化固有频率有较强相关性的 7个傅里叶描述子的相关系数如表2所示。

表2 归一化固有频率和傅里叶描述子间的相关性Table 2 Correlation between the normalized frequencies and the Fourier descriptors

由图11可知，归一化固有频率fn与果形系数间关系可用下式表示

式中fn为归一化固有频率，S为果形描述子，a和b的取值由振型决定，各阶振型对应a和b取值见图11。

2.4 啤梨硬度评估指标的构建

果蔬硬度可用弹性模量E表征，且频率f的平方与弹性模量E成正比[27-28]，故下式成立：

经转换可得

将公式（1）和（11）代入公式（13），得

式中m0为常数，a、b值由图11获得，EFEM为有限元模拟弹性模量值，取2.1.2节计算Eest的平均值6.86 MPa，代入公式（14）中得到硬度评价指标SE：

图12为啤梨在赤道部感测的振动频谱曲线，共振频率fBE为弯曲模态的频率，其对应加速度幅值不突出试验时不易提取。挤压模态的共振频率fC的加速度幅值很高，试验时非常容易提取。因此，在应用新的硬度评价指标检测啤梨时，评价指标中a、b分别取图11中挤压模态对应的值。

2.5 各频率指标对啤梨硬度的评价能力比较

啤梨在室温条件下硬度随储藏时间变化规律如图13所示，由图可知啤梨M-T穿刺硬度在12 d内总体呈现先快后慢的下降趋势，M-T穿刺硬度在前6 d内急剧下降，6～12 d之间硬度下降速度减缓。

将纵横比q和F1代入公式（15）获得含有果形描述子的硬度指标SE(q)和SE（F1），由1.8节方法对基于频率的硬度指标与M-T穿刺硬度SMT进行线性回归分析，结果如图14所示。传统单频硬度评估指标Sf与 M-T穿刺硬度SMT的决定系数较低（R2=0.733），啤梨试样不规则果形可能是导致单频指标Sf硬度评估值与M-T穿刺硬度实测值相关性不高的原因。

Cherng等[3]提出的双频硬度评价指标SCherng和笔者团队研究提出的双频指标Sf1f2与 M-T穿刺硬度SMT的决定系数R2非常接近，分别为0.775和0.765，较传统单频硬度评估指标而言，与硬度实测值SMT相关系数有所提高，但由于这 2种硬度指标都只能消除近椭形果形对频率的影响，相关系数提高效果并不显著。采用新硬度指标SE评估啤梨硬度时，以纵横比q和傅里叶描述子F1作为啤梨果形描述子分别带入新指标SE计算获得的指标SE(q)与M-T穿刺硬度SMT的决定系数R2值为0.746，指标SE（F1）与 M-T穿刺硬度SMT的决定系数R2值为 0.892，在各指标中最高。这表明傅里叶描述子能准确描述不规则果形梨果，本研究提出的硬度评价指标SE（F1）更适于复杂且不规则果形的啤梨硬度评估。

3 结 论

1）啤梨振动试验模态分析获得弯曲模态、挤压模态和呼吸模态，弯曲模态和呼吸模态在赤道部振动变形较小，挤压模态振动变形在赤道部变形较大，采用加速度传感器在赤道部感测时更易于获得挤压模态的共振频率。

2）采用前 15个傅里叶描述子足以描述啤梨外形特征，第1个傅里叶描述子F1与啤梨弯曲模态、挤压模态和呼吸模态归一化固有频率高度线性相关，线性相关系数r分别为−0.923、−0.922、0.700，较适于描述啤梨复杂果形的变化。

3）基于挤压模态的共振频率（fC）和傅里叶描述子F1构建硬度指标SE(F1)，可消除果形对啤梨硬度评估的影响。与其他研究报道的频率评估指标相比，该硬度指标检测啤梨硬度值与M-T穿刺法检测硬度值的决定系数R2为0.892，可用于果形复杂梨果硬度的较精确评估。