基于COA-ASRCKF的单液流锌镍电池SOC估计
宋春宁,苏有平,莫伟县,郑少耿
(广西大学电气工程学院,广西 南宁 530004 )
单液流锌镍电池的结构简单、循环寿命长、能量转换效率高、功率可灵活设置,且没有离子交叉污染,在应急电源系统、电站储能和智能电网等方面,具有潜在的应用前景[1]。
荷电状态(SOC)是电池状态的重要指标之一,准确估计电池SOC,既是电池管理系统的基本要求,也可提高电池的使用效率,避免过度充放电对电池的损坏[2]。卡尔曼滤波算法基于电池的状态空间模型,通过递推迭代估计SOC,对状态初始值误差有很强的修正作用,还可根据系统观测量,不断修正估算的系统状态量,对系统噪声的抑制作用较强[3]。文献[4]使用近似二阶扩展卡尔曼滤波(ASEKF)对锂离子电池进行SOC估计,误差估算精度小于2%。文献[5]基于H∞滤波器(HIF)在线估计电池模型参数,并使用无迹卡尔曼滤波(UKF)估计电池SOC,提出应用于电动汽车运行工况下SOC估计的HIF-UKF算法。文献[6]在容积卡尔曼滤波(CKF)的基础上,增加实时自适应修改过程噪声协方差Q和量测噪声协方差R的功能,提出了自适应容积卡尔曼滤波(ACKF),用于锂离子电池SOC估计。CKF[6]是电池SOC估计的常用方法,但在迭代过程中存在破坏协方差对称性和正定性的敏感操作,从而导致算法终止[7],且不更新量测噪声协方差R会造成估算误差累积,因此,要根据经验来设定过程噪声协方差Q、量测噪声协方差R和状态误差协方差P。
本文作者在CKF算法中增加平方根滤波,确保协方差在迭代过程中保持正定性,对量测噪声协方差R进行自适应更新,提出自适应平方根容积卡尔曼滤波(ASRCKF)算法;并应用郊狼优化算法(COA)[8]对ASRCKF算法的过程噪声协方差Q、量测噪声协方差初值R(0)及状态误差协方差初值P0进行参数寻优,以提高SOC估计精度和算法的鲁棒性;提出COA-ASRCKF算法,用于单液流锌镍电池的SOC估计。
1 单液流锌镍电池等效电路模型
采用等效电路模型对单液流锌镍电池进行建模。等效电路模型的选取,通常需要在复杂性和精度两个方面进行平衡[9]。理论上模型阶次越高,越能准确反映电池充放电时的内部反应,但阶次过高会使计算过程太复杂、实时性下降。选用二阶等效电路模型,可获得相对较好的估算精度和简单的计算过程。单液流锌镍电池的等效电路模型见图1。

图1 单液流锌镍电池的等效电路模型
图1中:Uoc为电池的开路电压(OCV),通常被看作SOC的非线性函数[9];R1为电化学极化电阻;C1为电化学极化电容;R2为浓差极化电阻;C2为浓差极化电容;R0为电池的欧姆内阻;i为放电电流;Ucell为电池端电压。
假设UR1C1表示电化学极化电压,UR2C2表示浓差极化电压。根据基尔霍夫定律,得到式(1)。
(1)
电池SOC安时积分法的定义为:
(2)
式(2)中:t为放电时间;η为电池的库仑效率;Cn为电池的额定容量;Soc(0)为电池SOC(Soc)初值。
该模型是非线性模型,为准确地辨识出模型参数,采用文献[10]中的递推最小二乘(RLS)法进行模型参数辨识。
2 基于COA-ASRCKF的电池SOC估计
2.1 ASRCKF算法
ASRCKF算法在CKF算法的基础上增加平方根滤波和量测噪声协方差更新,当初始条件选择不当或工况发生变化时,ASRCKF自适应更新量测噪声协方差,用于对下一状态的估计,以适应外部变化,提高算法的鲁棒性和估计精度。
ASRCKF算法的系统状态空间表达式见式(3)。
(3)
式(3)中:xk、yk分别为系统状态量和观测量;uk为输入量;f、g为非线性函数;wk-1、vk分别为过程噪声和量测噪声。
ASRCKF算法的具体步骤如下。
①初始化
S0=chol(P0)
(4)
②计算容积点Xj,k
(5)
式(5)中:Sk为状态误差协方差P在k时刻的平方根;n为系统状态量的维数;En为n阶单位矩阵;ξj为权值矩阵[En,-En]的第j列;Xj,k为第j个容积点k时刻的值。
(6)
④计算状态误差协方差平方根预测值
(7)
(8)
(9)
式(9)中:Yk+1为k+1时刻观测量的测量值;Rk为k时刻量测噪声协方差;χk+1、SR、rk+1为计算过程的中间变量。

(10)
⑧更新下一时刻量测噪声协方差Rk+1
(11)
式(11)中:ek+1为k+1时刻的测量值与预测值的差值;L为动态窗口的长度,L越大计算量越大,精度也越高。实验时,设置L=2。
重复循环步骤②-⑧,对系统状态量进行迭代估计。
2.2 ASRCKF算法估算电池SOC
根据式(1)、(2),选取[UR1C1,k,UR2C2,k,Soc,k]T作为系统状态量,建立单液流锌镍电池等效电路放电模型离散化方程,见式(12)。
(12)
式(12)中:T为系统采样时间,设置为1 s。
使用ASRCKF算法估算单液流锌镍电池SOC时,设置观测量yk=Ucell,k,状态量xk=[UR1C1,k,UR2C2,k,Soc,k]T,输入量uk=ik。非线性函数f、g的函数关系见式(13):
(13)
式(13)中:Uoc(Soc,k)表示Uoc关于SOC的函数关系。
ASRCKF算法通过迭代更新,计算单液流锌镍电池每个时刻的SOC估计结果。
2.3 COA-ASRCKF估计电池SOC
根据式(11)可知,在ASRCKF算法估计电池SOC时,过程噪声协方差Q和状态误差协方差初值P0均是3维变量,量测噪声协方差初值R(0)是1维变量。参数Q、R(0)和P0对状态量的估计精度具有重要影响,选取时通常是根据经验进行设定。根据经验设定参数不仅需要耗费一定的时间,且当参数设定不当时,还会导致算法性能下降。针对这一现象,应用郊狼优化算法(COA)对Q、R(0)和P0进行参数寻优,以提高电池SOC的估算精度和算法鲁棒性,并提出COA-ASRCKF算法,用于单液流锌镍电池SOC估计。
2.3.1 郊狼优化算法(COA)
COA是由J.Pierezan等[11]提出的一种模拟郊狼群居生活、成长、生死等现象的算法,具有独特的搜索模型和结构,优化能力出色,在解决复杂优化问题时优势明显[8]。在COA中,每头郊狼代表一个候选解,每个解向量由郊狼的社会状态因子构成,每一个状态因子代表一个决策变量,D个状态因子构成了一个含D个决策变量的解向量,用社会适应度评价每头郊狼。COA主要分为4个步骤:初始化郊狼群、组内郊狼成长、郊狼的出生与死亡和郊狼被组驱离与接纳。
①初始化郊狼群

(14)

②组内郊狼成长
组内郊狼成长主要靠组内最优狼Ga、组文化趋势Cu及随机选取的组内两头郊狼rc1、rc2,Cu的计算见式(15)。
(15)
式(15)中:O为郊狼种群按适应度升序排列后的社会状态因子。
郊狼成长公式见式(16)。
(16)
(17)
采用式(18)进行优胜劣汰,以保留对应更优郊狼。
(18)
③郊狼出生与死亡
每组郊狼成长后会产生一只新生郊狼(Gu),新生郊狼受随机选择的父母郊狼rc3、rc4的遗传基因及社会环境影响,数学模型见式(19)。
(19)
式(19)中:Mj为第j个决策变量取值范围内的随机数;rj为由均匀概率产生的[0,1]内的随机数;Grc3,j、Grc4,j为组内两个不同的郊狼的第j维;j1、j2为两个随机选择的维度标号;Ps和Pa分别是分散概率和关联概率,决定着幼狼被遗传和变异的情况,计算公式见式(20)。
(20)
幼狼Gu出生后开始评价社会适应能力,若适应能力比组内适应能力最差、年龄(Aage)最老的郊狼(G0)好,则淘汰G0留下Gu,并将Gu的年龄置0,否则Gu淘汰。
④郊狼被驱离与接纳
随机分配到各组的郊狼,会以一定的概率被驱离并与其他组内的某郊狼交换。该机制有助于各组郊狼的交流。被驱离和接纳的概率Pe见式(21)。
(21)
在初始化并随机分组后,依次不断进行②、③、④这3个步骤,当达到迭代终止条件输出最优郊狼,否则跳转到②。
2.3.2 COA-ASRCKF估算电池SOC求解模型
COA-ASRCKF算法估计电池SOC求解模型如下:
将COA算法中郊狼设置为ASRCKF算法中的参数R(0)、P0=diag([PL1,PL2,PL3])、Q=diag([QL1,QL2,QL3]),即郊狼=[R(0),PL1,PL2,PL3,QL1,QL2,QL3];将郊狼代入ASRCKF算法,计算电池SOC估计值,以安时积分法估算的电池SOC作为参考值,根据式(22)计算郊狼的适应度fit。
(22)

用COA-ASRCKF算法估算单液流锌镍电池SOC的伪代码见表1。

表1 COA-ASRCKF算法的伪代码
3 实验验证及结果
以单液流锌镍电池(张家港产)为研究对象,额定容量为210 Ah,充电终止电压为2.1 V,放电截止电压为1.2 V,尺寸为22 cm×21 cm×19 cm。用CT-3004-5V200A-NTFA电池综合测试仪(深圳产)进行脉冲恒流放电实验[12],实验环境温度为25 ℃,设置电池初始SOC=0.95,放电截止SOC=0.05,脉冲放电步进增量为电池额定容量的5%(共18个放电脉冲),放电电流为100 A,搁置时间为5 min,采样周期为1 s。
3.1 OCV-SOC曲线
单液流锌镍电池的OCV与SOC具有非线性函数关系。用脉冲恒流放电试验来标定开路电压曲线,将每个放电脉冲结束并静置至端电压Ucell稳定后的值,作为电池的开路电压Uoc。通过脉冲放电曲线可获得电池OCV和SOC的数据,通过MATLAB的cftool工具箱,对实验数据进行多项式拟合,得到电池放电状态下Uoc与SOC函数表示式,见式(23)。
(23)
3.2 基于COA-ASRCKF电池SOC估计仿真分析
将采集到的实验数据导入MATLAB,设置郊狼群规模N=100、郊狼组数Np=10、组内郊狼数Nc=10、最大迭代次数tmax=10 000等参数,电池等效模型参数根据辨识结果确定;COA-ASRCKF算法参数Q、P0、R(0)根据COA算法寻优获得;ASRCKF算法和CKF算法参数Q、P0、R(0)依据经验设定,具体取值均为Q=diag([1×10-6,1×10-25,4×10-50]),R(0)=3×10-7,P0=diag([0.01,0.01,0.01])。设置SOC正确初值(SOC=0.95)和错误初值(SOC=0.50),得到的仿真结果见图2。
从图2可知,在SOC初值设置正确(SOC=0.95)的情况下,使用COA算法寻优得到参数Q、P0、R(0)的COA-ASRCKF算法,相较于根据经验来设置参数的ASRCKF算法和CKF算法,估计精度更高;在SOC初值设置错误(SOC=0.50)的情况下,相较于CKF算法和ASRCKF算法,COA-ASRCKF算法估算电池SOC的鲁棒性更强,同时估计精度也更高。CKF算法由于量测噪声协方差固定不变,导致估计误差累积,在SOC估计末端估计误差明显增大。

图2 SOC初值为0.95和0.50的估计结果对比
为更加清晰直观地比较3种算法在对电池SOC估计过程中的估计精度和鲁棒性,设置电池SOC错误初值为0.50,并将3种算法的SOC估计结果与参考值进行差值计算,得到SOC估计误差结果,见图3,电池SOC估计评价指标见表2。
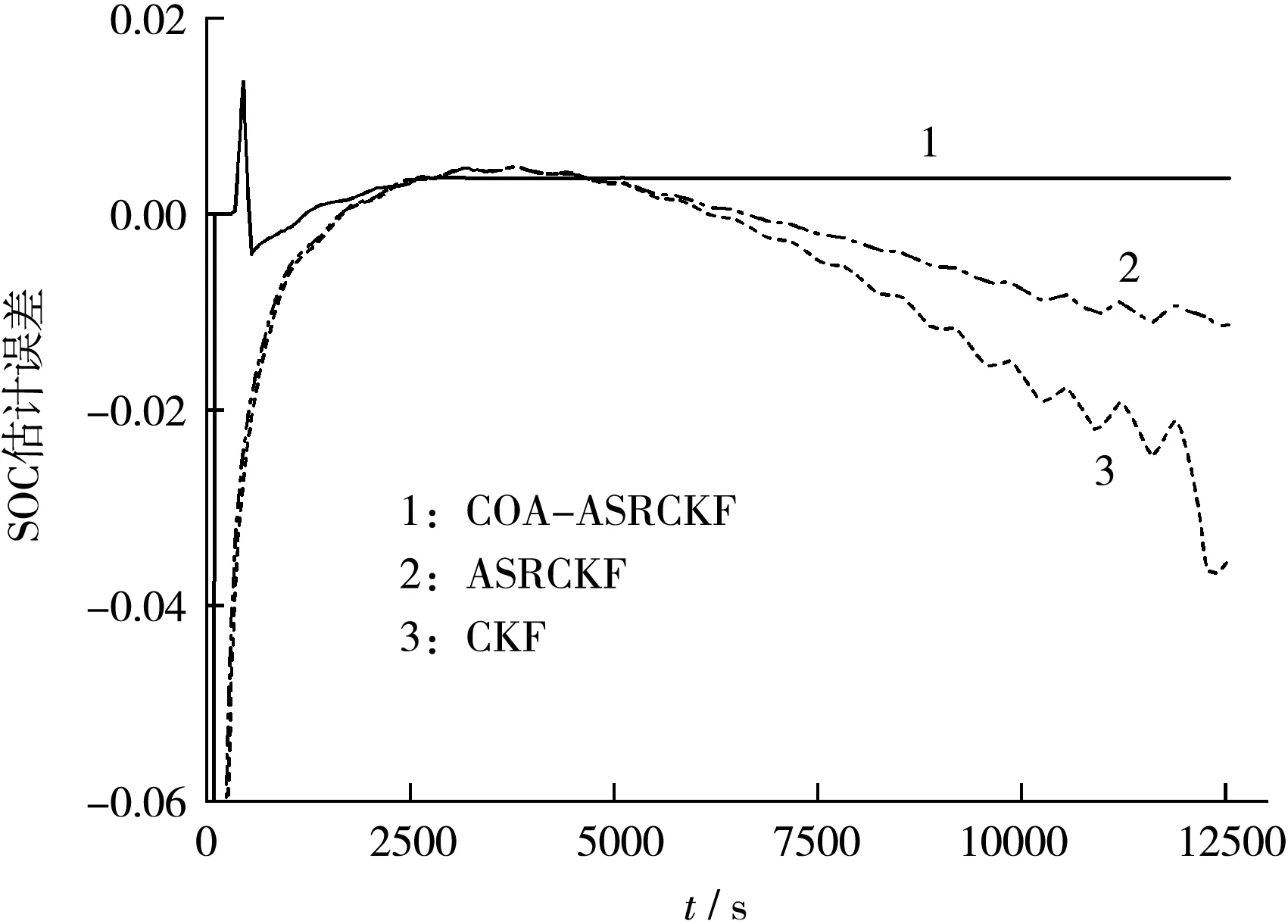
图3 SOC初值为0.50的估计误差对比
从图3可知,在SOC估计过程中,COA-ASRCKF算法的鲁棒性和估计精度优于CKF算法和ASRCKF算法。
从表2可知,不论电池SOC初值设置正确与否,COA-ASRCKF算法的均方根误差均小于ASRCKF算法和CKF算法。
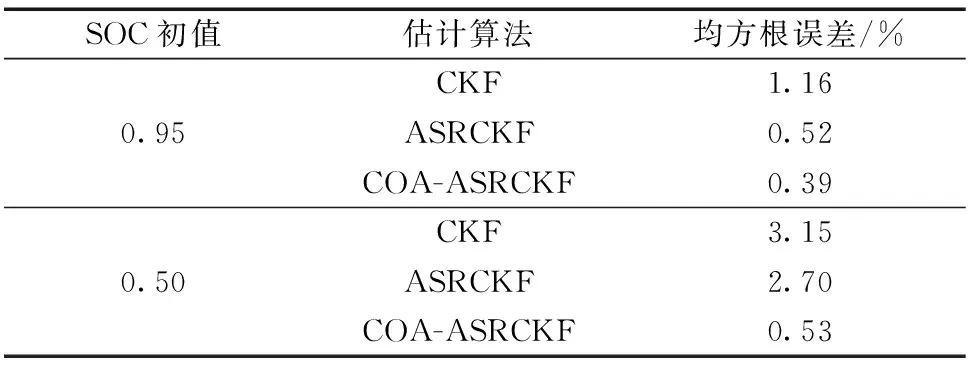
表2 SOC估计方法评价指标
4 结论
在CKF算法中加入平方根滤波及自适应更新量测噪声协方差R,并使用COA算法对卡尔曼方程的过程噪声协方差Q、量测噪声协方差初值R(0)及状态误差协方差初值P0进行参数寻优,提出COA-ASRCKF算法用于单液流锌镍电池SOC估计。该算法在估计单液流锌镍电池SOC时,相较于ASRCKF算法和CKF算法,具有更高的估计精度和更强的鲁棒性,可在初值错误的情况快速修正,估计均方根误差小于1%。在研究过程中,假定参数不变且未考虑电池受老化及电解液流速的影响,在后续研究中可考虑添加这两个内容。

