数字普惠金融发展的动态演进及趋势预测研究——以珠三角城市群为例

程风雨

（广州市社会科学院 区域发展研究所，广东 广州 510410）

十九大报告指出，创新是引领发展的第一动力。在经济发展新阶段，中国经济发展更离不开创新驱动，需要提升全社会科技创新能力，进一步优化产业结构，推动经济发展模式由粗放式增长逐步转变为以创新为驱动的内涵式增长。其中，区域创新活动需要多渠道资金，而数字普惠金融可以为其提供重要的资金支持。依托信息技术和大数据的发展，数字普惠金融打破了传统金融资源的空间限制，在为区域创新活动拓宽融资渠道的同时，极大地提升了地区金融服务的正向外溢效应［1］。

作为我国改革开放的前沿和金融创新发展的核心区域，珠三角城市群发展数字金融的优势较为明显，随着《粤港澳大湾区发展规划纲要》的公布实施，其金融资源的趋利性、自由性和高速流动得到了极大提高，珠三角城市群对于我国经济转型升级具有愈发重要的典范作用。伴随着数字信息技术的不断升级，数字普惠金融对地区资源配置的影响更加突出。在此背景下，有必要以珠三角城市群为研究对象，探究数字普惠金融发展的非均衡性，研判其短期和长期的动态演进趋势。

1 文献综述

《中国普惠金融发展报告（2016）》明确指出，任何以数字金融为途径实现金融普惠的行为都可以纳入数字普惠金融的界定范畴。有学者对数字普惠金融的性质进行了总结，认为数字普惠金融是金融普惠与数字经济高级阶段融合的产物，其不仅具有商业属性，还具有社会价值［2，3］。从既有研究来看，对数字普惠金融问题的探讨主要是从两个方面展开：①定量测度与评价。较早的研究是从金融排斥的视角出发，借鉴联合国开发计划署的人类发展指数（HDI）的体系方法对普惠金融加以测度。如，Sarma基于银行渗透度、服务的可利用性和使用状况3 个维度，构建了国别层面的普惠金融发展指数［4］；张国俊、周春山、许学强从金融服务渗透度、使用度、效用度、承受度4 个维度构建了中国省际普惠金融指标体系［5］。国内相关研究主要是直接针对金融服务的“包容性”进行测度研究。其中，主流测度指标是2016年由北京大学互联网金融研究中心联合蚂蚁金服发布的《北京大学数字普惠金融指数》（年度序列）数据。该数据基于互联网金融服务的覆盖广度、使用深度和数字支持服务3 个维度，成为国内开展数字普惠金融定量研究的权威数据之一［6］。②对宏观经济社会发展的影响。主流研究认为数字普惠金融能够显著促进经济增长［7］，对居民消费支出［8］、城乡收入差距［9］、贫困减缓［10］、包容性经济增长［11］、家庭风险金融资产投资［12］等产生正向影响。由于相关法律法规建设的滞后和政府监管不到位等问题，作为数字金融的新型金融业态，数字普惠金融仍具有较大的风险性和不确定性［13，14］。

通过文献梳理可以发现，目前关于数字普惠金融发展的研究主要存在以下局限：一是较多学者重点关注数字普惠金融发展的地区差异及动态演进特征［15，16］，但未能对其长期趋势加以预测和分析；二是主要针对的国家或省级层面，而基于城市群层面的数字普惠金融发展的研究鲜见；三是数字普惠金融发展的动态演进规律分析大多忽略了空间因素的影响，而空间溢出效应考察不足则可能导致研究结论产生较大偏误。与已有相关研究相比，本文可能的边际贡献主要在于：①将研究尺度进一步降为城市群和城市尺度，使得我国数字普惠金融研究更加具体和富有针对性。②在传统Markov 链方法的基础上，采用空间Markov链就空间因素分析数字普惠金融发展的影响，更加科学地对数字普惠金融发展的长期演进趋势进行预测。③结合马尔科夫链方法，使用面板分位数回归模型来研究不同条件下数字普惠金融发展的驱动因素，从而为有效推动区域数字普惠金融协调发展提供政策参考。

2 研究方法与数据来源

2.1 研究方法

Kernel密度估计法：作为非参估计方法的一种，Kernel密度估计没有确定的表达式，往往是通过估计值的图形分布变化来反映考察对象的动态变化。具体而言，其主要是考察曲线的分布位置、形态、延展性和极化程度的改变。对比不同样本期的核密度分布曲线图，如果曲线整体位置向右偏移，意味着考察对象发展程度总体呈增长趋势，如果向左偏移，则意味着发展程度总体呈现减少趋势；曲线主峰高度和宽度的改变，反映了考察对象发展的绝对差异；曲线的右向倾斜的延展状态意味着考察对象的相对差异的改变，而曲线波峰数量的多寡则可以说明考察对象极化程度的变化。

借鉴Silverman的研究［17］，构建随机变量X的密度函数：

式中，Xi为满足独立同分布的观察值；N和h分别为观测值的数量与带宽；x 为均值；K（·）为核函数，需要同时满足以下条件：

在现有研究中，作为一种平滑转换函数或者加权函数，核函数通常有三角核函数、高斯核函数、Epanechnikov核函数等，而现有研究较多采用高斯核函数。据此，本文基于高斯核函数进行Kernel 密度估计，表达式为：

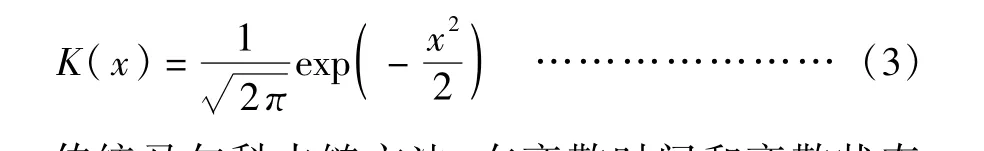
传统马尔科夫链方法：在离散时间和离散状态条件下，传统马尔科夫链是一个满足｛X（t），t∈T｝的随机过程。马尔科夫链的取值是由所有元素为随机过程状态组成的有限集合X，该集合对应于各个时期。令随机变量X－｛t｝＝j，即随机变量在时期的系统状态为j的概率需要满足如下性质条件：

可以看出，作为一种特殊的随机过程，上述一阶马尔科夫链的动态行为的特征是当前状态Xt的条件分布只依赖于前一期状态Xt－1。假设Pij为珠三角城市群某一样本城市数字普惠金融从t 时期的i类型转移到t ＋1 时期的j 类型的转移概率，并采用式（5）形式下的极大似然估计法求出该值：

式中，nij为样本考察期内由t时期属于i类型转移到t ＋1 时期属于j 类型的样本城市数量；nj为t ＋1时期属于j类型的样本城市数量。将珠三角城市群数字普惠金融发展状态划分为N 种类型，构造出N×N的马尔科夫转移概率矩阵，据此分析每种类型的的转移概率，从而揭示珠三角城市群不同水平数字普惠金融的动态转移趋势及其演变特征。

空间马尔科夫链法：空间马尔科夫链法是将“空间滞后”的概念引入传统马尔科夫分析过程而产生的［18］，可以用来考察空间效应对珠三角城市群数字普惠金融动态演变的影响。具体方法：通过设定空间权重矩阵来衡量珠三角城市群某一样本城市的邻近城市数字普惠金融水平。在此，本文采用地理邻接空间权重矩阵（W），并做行标准化处理。W 单位元素设定形式如下：

式中，k 为类型分类数；mij为传统马尔科夫转移概率；mij（l）和nj（l）分别为空间滞后类型为l 的空间马尔科夫转移概率和相应的城市个数；M 为服从转服从自由度为k ×（k－1）2的卡方分布。其原假设为：珠三角城市群数字普惠金融类型是相互独立的，与空间滞后类型无关。

2.2 变量设置及数据说明

本文采用2011—2018 年珠三角城市群数字普惠金融的面板数据，选取广州、佛山、肇庆、深圳、东莞、惠州、珠海、中山和江门9 个城市作为细分研究个体。其中，数字普惠金融数据来源于北京大学互联网金融研究中心编制的《北京大学数字普惠金融指数（2011—2018）》。参考宋晓玲［21］，葛和平和朱卉雯［22］，蒋庆正、李红、刘香甜［23］的研究，考虑到城市层面数据的可获得性，确定以下对珠三角城市群数字普惠金融的影响因素：①地区经济增长。采用Chen Z、Yu B、Yang C 等的最新研究成果［24］，处理得到历年样本城市的夜间灯光数据并加以衡量，更加贴近现实发展。②收入水平。一般来说，收入水平越高，越有机会接触到各种金融服务，选取地区职工平均工资来表示。③区位综合因素。交通、通讯和地理距离等会影响金融服务的可达性，而人口密度可最大程度地融合并反映出上述作用，因此采用地区人口密度加以衡量。④金融资产。金融资产的多少会直接决定金融产品的选择组合，采用城乡居民储蓄年末余额规模表示。⑤教育水平。教育水平会对金融自我排斥产生重要影响，采用万人之中具有高等学历的占比表示。⑥互联网使用。采用每百人中的互联网使用人数作为互联网发展情况的衡量指标。上述指标数据均来自2012—2019 年《中国城市统计年鉴》、Wind数据资源库和EPS数据平台。

3 珠三角城市群数字普惠金融的发展演进

3.1 数字普惠金融分布动态演进

本文采用高斯核函数进行Kernel 密度估计，并对不同时期城市群数字普惠金融的分布位置、态势、延展性和极化趋势进行考察，以便整体把握珠三角城市群数字普惠金融分布形态，探究其分布动态特征。为确保核密度非参数估计结果的精准性，本文将城市群样本期的每一观察年的数字普惠金融指数作为观测样本。珠三角城市群数字普惠金融的动态演进趋势见图1。

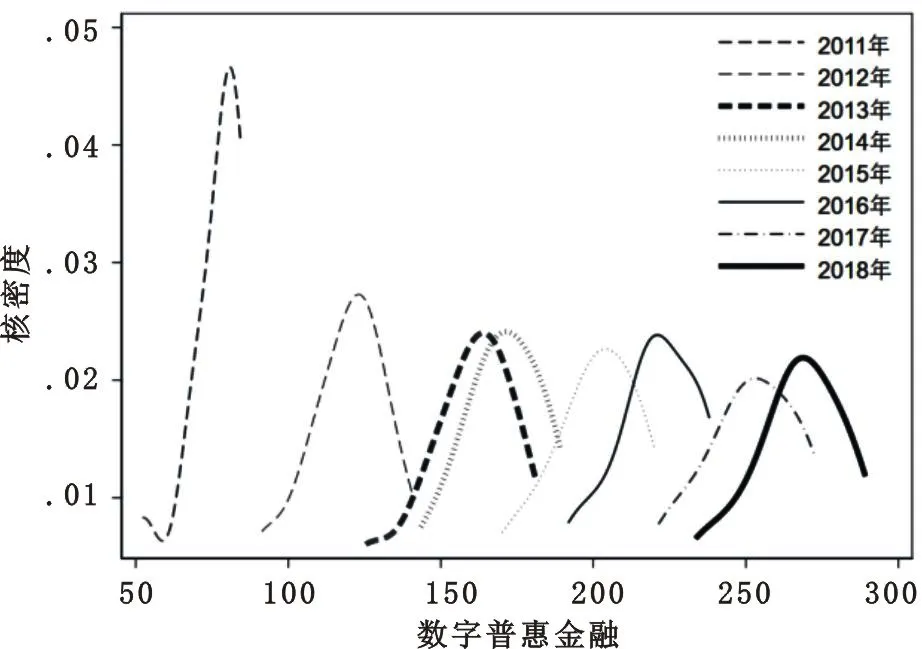
图1 珠三角城市群数字普惠金融的核密度分布动态演进

在观测期内，珠三角城市群数字普惠金融的分布动态呈现如下特征：①从分布位置来看，珠三角城市群分布曲线随时间推移整体向右边小幅渐进移动，说明城市群数字普惠金融发展由低水平向高水平不断演进。②从分布曲线的波峰态势来看，珠三角城市群分布曲线主峰峰值呈波动下降趋势，且曲线宽度表现为先窄后逐渐加宽的变化过程，意味着城市群数字普惠金融总体离散程度呈扩大趋势，即其绝对差异随着时间的推移呈扩大态势。③从分布曲线的延展性得知，不同时期珠三角城市群总体分布曲线均不存在明显右拖尾现象，表明城市群数字普惠金融发展程度较高城市与较低城市之间的相对差距有所缩小，即分布延展性呈现收敛趋势。④从极化特征来看，不同时期珠三角城市群分布曲线波峰数量一直呈现单峰现象，意味着城市群数字普惠金融发展不具有一定的梯度效应，即不具有多极化特征，两极分化趋势较为明显。总体而言，随着珠三角城市群经济社会快速发展，数字普惠金融发展总体呈现显著提升，但城市群内部之间的发展差距仍然存在，短期内实现均衡发展存在较大难度。

3.2 数字普惠金融发展趋势预测

本文尝试采用传统Markov 链方法展开分析。首先在样本期内逐年将城市群数字普惠金融发展程度按高低划分为低水平（L）、中低水平（ML）、中高水平（MH）和高水平（H）4 个等级，然后以滞后一年的条件获得珠三角城市群数字普惠金融转移概率矩阵，结果见表1。

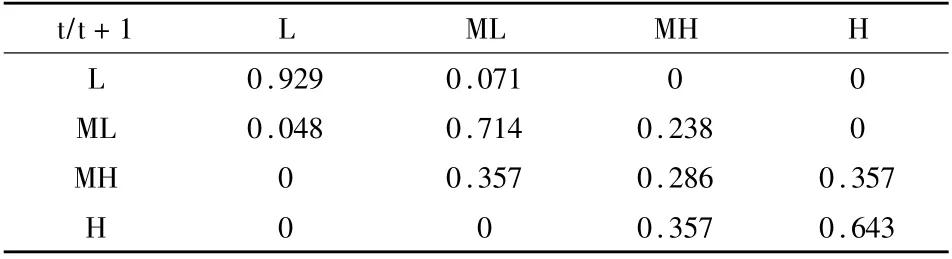
表1 传统马尔科夫转移概率矩阵

从表1 可见，92.9%的珠三角城市群一年后数字普惠金融仍保持在低水平，7.1%的城市将转移至中低水平，但没有城市有机会跳跃至中高水平和高水平阶段；71.4%的城市一年后数字普惠金融指数仍保持在中低水平，向低水平和中高水平转移的概率分别为4.8%和23.8%，同样没有城市有机会跳跃至高水平阶段；28.6%的城市一年后数字普惠金融仍保持在中高水平，开始出现向高水平转移的现象，其概率为35.7%，向中低水平反向转移的概率分别为35.7%，没有城市倒退转移到低水平阶段；64.3%的城市一年后数字普惠金融仍保持在高水平，35.7%的城市反向转移到中高水平，没有城市由高水平转移到低水平和中低水平。

通过以上分析结果可知：①数字普惠金融发展存在较为显著的收敛性特征，且城市群内部之间不存在发展的“马太效应”。②正向转移的概率随着数字普惠金融发展程度的提高而显著增加，低水平、中低水平和中高水平的正向转移概率从7.1%分别增加到23.8%和35.7%，意味随着数字金融普惠发展程度的提高，珠三角城市群数字普惠金融优化升级的概率也会大大增加。③非对角线上的转移概率值均分布于对角线两侧，其概率值最小为0，最大为35.7%，意味着珠三角城市群数字普惠金融发展是一个缓慢且渐进的过程，在短时间较难实现跨越式发展，这也与Kernel密度估计结果相一致。

4 影响因素分析

4.1 数字普惠金融转移的驱动因素

鉴于上述传统Markov链分析，将珠三角城市群的全体样本城市按数字普惠金融数值大小平均划分为低水平、中低水平、中高水平和高水平4 个等级，相应的，本文尝试在25%、50%和75%3 个分位点处计算回归结果，以分析在不同临界点处各驱动因素对城市群数字普惠金融的影响作用。分位数面板回归模型构建为：

式中，Y和xi分别表示样本城市数字普惠金融及其可能的影响因素；q 和βqi分别表示不同的分位点及该分位点上的回归系数。本文选择地区经济增长、收入水平、区位综合因素、金融资产、教育水平和互联网使用作为影响变量参与分位数回归，相关结果见表2。

表2 珠三角城市群数字普惠金融分位数回归结果

由表2 可知：①在25%分位点处，地区经济增长的回归系数为－0.032，说明地区经济增长未必一定可以带动数字普惠金融发展，这与李涛、徐翔、孙硕的研究［25］相一致。收入水平和区位综合因素的回归系数分别为0.462 和0.076，这说明这两个因素均有利于提高数字普惠金融水平。除了金融资产和教育水平外，其他因素均没有通过至少10%的统计性水平检验。虽然绝大多数因素对城市数字普惠金融发展具有积极推动效用，但影响并不显著，从而无法有效拉动低水平城市数字普惠金融转移至中低水平，呈现低水平趋同特征。这也从一定程度上印证了珠三角城市群一年后数字普惠金融仍保持在低水平概率为最大的结论，表明城市群数字普惠金融低水平趋同较为稳定。②在50%分位点处，除了地区经济增长以外，其他影响因素均可以正向推动城市群数字普惠金融发展，且收入水平和金融资产均通过1%统计水平检验。教育水平在10%统计水平上显著，说明绝大多数影响因素能够有效拉动城市群数字普惠金融从中低向中高水平转移。③在75%分位点处，同样绝大部分影响因素对城市群数字普惠金融的发展具有推动作用，但与50%分位点上的回归结果相比，仅有收入水平和金融资产在1%统计水平上显著。由此可知，在城市群数字普惠金融从中高水平向高水平转移过程中，各影响因素使中高水平城市大多保持在原有水平，从而形成了中高水平趋同。

4.2 空间因素的影响

由于区域间数字普惠金融发展水平存在一定的地理相关性，因此有必要将空间因素考虑在内，建立空间马尔科夫转移概率矩阵。据此，本文将基于行标准化后的邻接地理空间权重矩阵，在样本期的每一年里，按照珠三角城市群数字普惠金融发展程度高低平均划分为4 个等级，以滞后一年的条件计算得到珠三角城市群数字普惠金融指数的空间转移概率矩阵（表3），并展开深入分析。

由表3 结果可知，空间效应对珠三角城市群数字普惠金融发展的影响主要体现为：①地理空间因素对珠三角城市群数字普惠金融发展各类型间的动态转移具有较为显著的影响。当不考虑地理空间因素时，低水平类型向中低水平类型转移的概率为7.1%；当考虑地理空间因素时，低水平类型向中低水平类型转移的概率依次为0、0、14.3%和0。因此可见，将地理空间因素纳入珠三角城市群数字普惠金融发展的动态演变趋势分析中是必要的。②随着邻接城市发展类型的不同，数字普惠金融在同一类型中的稳定性会存在明显的差异。对于低水平类型而言，其在邻接类型L、ML、MH、H 中稳定性概率依次为100%、0、85.7%和0；对于中低水平类型而言，其在邻接类型L、ML、MH、H中稳定性概率依次为0、66.7%、71.4%和100%；对于中高水平类型而言，其在邻接类型L、ML、MH、H 中稳定性概率依次为0、28.6%、28.6%和0。对于高水平类型而言，其在邻接类型L、ML、MH、H 中稳定性概率依次为0、75%、0 和0。此结果表明，在考虑地理空间因素后，数字普惠金融发展在L、ML、MH、H类型中的稳定性会随着邻接类型的提高而变差。③邻接地区数字普惠金融发展的提高可以提高本地区数字普惠金融发展向上转移的概率。在考虑地理空间因素的影响下，与数字普惠金融发展较高的地区为邻，其向上转移的概率均不会增大。此结果表明，数字普惠金融发展较高的地区对邻接地区不具有正向溢出效应，一定程度上不存在条件收敛特征。

表3 空间马尔科夫链转移概率矩阵

分析可见，珠三角城市群数字普惠金融存在一定的空间溢出效应，但这种空间溢出性是否在统计学上具有显著性，需要进行假设检验。在未调整自由度的情况下，自由度为36，根据公式（7）计算可得在1%统计水平上M ＝117.04 ＞x2（36）＝58.62。因此，拒绝接受在2011—2018 年珠三角城市群数字普惠金融类型转移在空间上是相互独立的原假设，表明邻近城市对于本地区数字普惠金融的转移存在着显著的影响。

5 结论与政策建议

主要结论：①总体而言，珠三角城市群数字普惠金融分布曲线的中心逐渐右移，表明其数字普惠金融发展呈现递增的趋势。②城市群数字普惠金融发展不具有多极化特征，两极分化趋势较为明显，但并未表现出明显的右拖尾分布，表明城市群内部之间的发展差距有所缩小。③随着数字金融普惠发展程度的提高，城市群数字普惠金融优化升级的概率会大大增加，但是短时间内想实现珠三角城市群数字普惠金融跨越式发展存在一定难度。④除了金融资产和教育水平外，地区经济增长、收入水平、区位综合因素和互联网使用等因素均较难以拉动低水平城市数字普惠金融转移升级，发展的低水平趋同现象较为稳定。⑤空间因素对于珠三角城市群数字普惠金融的动态转移具有一定影响，低水平的邻近城市会阻碍本地区的发展，甚至会拉低数字普惠金融水平，但高水平的邻近城市并未对本地区数字普惠金融发展起到正向拉动作用。

建议：①推动数字普惠金融相对落后城市的发展，逐步缩小城市群内部数字普惠金融发展差距。研究表明，珠三角城市群两级分化趋势依然明显，这意味着在更高水平上实现数字普惠金融协调发展的机制有待完善。因此，应正视数字普惠金融发展的区域不均衡问题，在尊重地方资源禀赋、经济社会发展阶段的前提下，加大对数字普惠金融相对落后的城市的扶持力度，利用数字普惠金融“包容性”特征，充分发掘数字普惠金融发展的后发优势，有效发挥数字普惠金融对地区经济社会发展的助推作用。②通过“涓滴效应”和“极化效应”，全面激发数字普惠金融发展水平较高城市的“梅特卡夫法则”效应。结合Markov链分析和分位数回归结果可知，珠三角数字普惠金融低水平发展阶段的趋同较为稳定，高水平发展阶段趋同却不稳定，其对邻近城市的正向空间溢出效应十分有限。一方面，高水平城市要加强自主创新，增加其数字普惠金融使用的广度、深度和数字化程度，通过“涓滴效应”服务周边城市发展；另一方面，要进一步扩大“极化效应”带来的发展优势，降低不同地区数字普惠金融发展的摩擦系数，推动数字普惠金融发展水平较高城市金融服务加速向更大范围扩散。③在“共享共赢”理念导向下搭建互动平台，努力推动区域数字普惠金融协同发展。根据不同地区的政府财力与经济发展水平，采取差异化的数字普惠金融能力提升策略，创新强数字普惠金融领域的交流互助和精准帮扶机制，促进地区间普惠金融“空间联动”发展。重点缓解因地方财政能力差异而导致的城市群内部数字普惠金融服务的非均衡状况，提高数字普惠金融服务的地区适应性和针对性，构建跨空间交流和互补体系。同时，要防范不同地区间对数字普惠金融资源的“逐顶竞争”，合理有序引导城市群内部发展数字普惠金融。