基于非下采样轮廓波变换的中子/X射线图像融合算法研究

贺林峰，张晓敏，武梅梅，林　强，袁石磊，刘晓光，杨　民,*

基于非下采样轮廓波变换的中子/X射线图像融合算法研究

贺林峰1，张晓敏2，武梅梅1，林强2，袁石磊3，刘晓光1，杨民2,*

（1. 中国原子能科学研究院，北京102413；2. 北京航空航天大学，北京 100191；3. 河南华探检测技术有限公司，河南郑州 450000）

由于中子与X射线的成像特性存在很好的互补性，将这两种成像模式下的DR（Digital Radiography）图像进行融合，可以丰富图像细节的信息量。本研究提出了基于简化脉冲耦合神经网络（PCNN）的非下采样轮廓波变换（NSCT）域中子/X射线图像融合算法，所提出的方法通过NSCT算法对源图像进行多尺度、多方向分解，有效地保留了各层信息，使得融合图像展现出良好的清晰度和对比度。同时，为了更好地保留源图像的信息，本研究对图像的不同频带分别采用取平均、绝对值取大和结合PCNN系数的融合规则进行融合。通过选取结构较为复杂的石英表、机械表以及结构相对较为简单的U盘进行中子与X射线图像采集，并利用多种客观评价指标定量评价基于小波变换融合、拉普拉斯变换融合、NSCT融合、NSCT-PCNN融合、Zhu的方法以及本文提出的方法生成中子与X射线融合图像的质量。实验结果证明，本文所提出的融合算法能够显著提高图像融合效果，获得清晰的目标信息，提高了图像对比度，同时保留丰富的细节信息，在客观评价标准和视觉效果上均优于其他典型方法。

图像融合；非下采样轮廓波变换；脉冲耦合神经网络；中子图像；X射线图像

X射线成像与中子成像作为两种重要的辐射成像方式，近些年来在材料学、生物医学、航空航天、汽车工业、电子、考古、安检等领域的无损检测中发挥着越来越重要的作用[1,2]。众所周知，X射线和中子与物质的作用机理不同，X射线作用于物质原子核外电子，其作用截面与核素的原子序数有确定的函数关系，而中子则是直接与原子核相互作用，散射截面大小与原子序数没有直接关系。由此可见，中子成像与X射线成像特性存在着很好的互补性，中子成像在检测含较轻元素的材料、原子序数相近元素等方面有着X射线无法具备的优势，而X射线在检测金属材料、高密度物质时具有更高的灵敏度。因此，对于检测含有金属和非金属材质的复杂结构样品，利用中子成像和X射线成像两种成像手段，可以获得样品更为全面的成分及结构信息。

图像融合是将不同场景的图像传感器获得的多源图像或同一场景中不同模式的图像进行信息合成，以获得具有多元信息的融合图像。与源图像相比，融合图像提取了来自多个图像的互补和冗余信息，因此，更加详尽地描述了场景信息[3]。所以，利用图像融合技术将中子成像与X射线成像得到的图像进行综合处理，可以丰富图像的边缘、纹理等细节信息，生成质量更高的图像。

本研究中，针对中子成像与X射线成像两种模式下的图像融合，提出了一种基于非下采样轮廓波变换（NSCT）分解的图像融合方法。通过NSCT对两种模式的图像进行多尺度、多方向分解后，我们对中子图像与X射线图像中低频子带、低层高频子带和顶层高频子带分别采用了不同的融合规则以保留图像更多的细节信息。在低频子带融合时，考虑到直接取平均会导致边缘信息不够精细，本文将Sobel边缘检测算法引入到低频子带融合系数的选取规则中。高频子带蕴含了输入图像中的细节信息和特征，采用绝对值取大规则可以保留丰富的细节信息，但是由于中子与X射线图像信噪比较差，噪声信息分解后高频系数较大，导致融合后图像噪声问题仍然明显。因此，在对高频子带系数进行选取时，在相对低层的高频子带中使用取大融合规则，保证待融合图像中原有的细节信息不丢失，而在顶层高频子带中使用简化的PCNN模型来选取融合系数，在该模型中，采用拉普拉斯能量和矩阵与能见度矩阵作为其链接强度，进而实现了对噪声的抑制。实验结果表明，所提出的方法在中子成像与X射线成像的图像融合中达到了较好的融合效果，不仅能够保留X射线图像的金属材料信息，而且可以展现中子图像的非金属材料信息，融合图像具有较高的对比度，目标信息显著，细节信息丰富。

1　基于非下采样轮廓波变换的中子/X射线图像融合算法

1.1　非下采样轮廓波变换

如图1所示，基于非下采样轮廓波变换（NSCT）分解过程由两个主要的部分组成，非下采样金字塔（Nonsubsampled Pyramid，NSP）与非下采样方向滤波器组（Nonsubsampled Directional Filter Bank，NSDFB），NSP负责对图像进行多分辨率分解，NSDFB则负责对图像进行多方向分解。首先采用NSP对图像进行多尺度分解，每经过一级NSP分解可产生一个低频子带和一个高频子带，NSP分解在低频子带上进行迭代以获取图像中的奇异点；然后对每一级的高频子带采用NSDFB进行多方向分解，将分布在同一方向上的奇异点合成为一个系数，从而得到不同尺度和方向的子带图像。

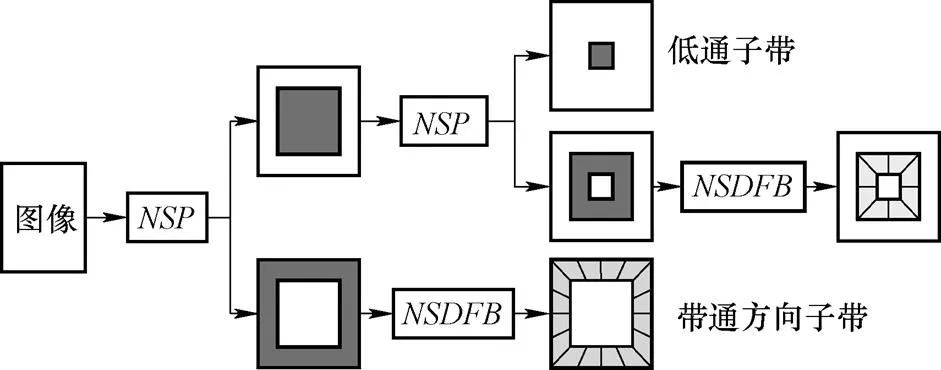
图1　NSCT分解过程示意图

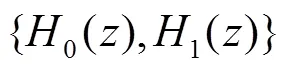
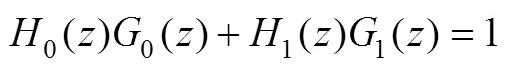
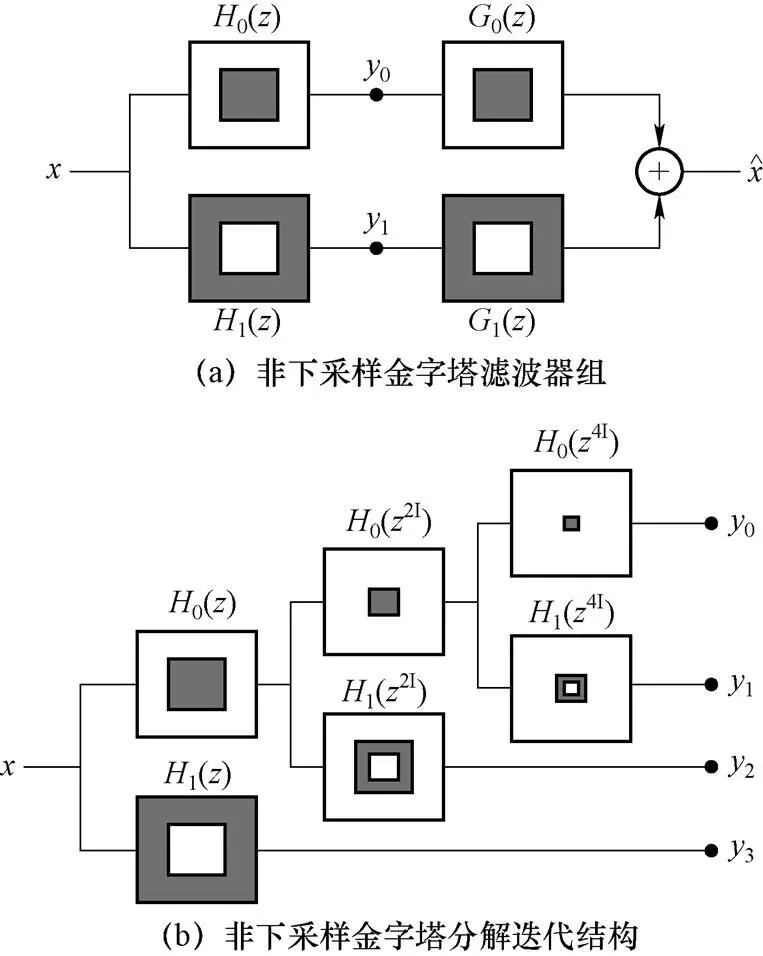
图2　非下采样金字塔

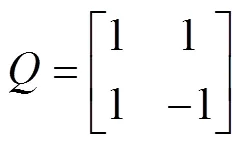
NSDFB分解过程中，非下采样方向滤波器组结构如图3（a）所示。

图3（b）所示为非下采样方向滤波器组的分解示意图。第一层为扇形滤波器组，第二层为象限滤波器组，经过二层滤波可以得到图像四个方向上的频率子带图，相应频带划分如图3（c）所示。如果在此基础之上对每一个得到的频率子带图进行双通道滤波，则可以得到八个方向上的频率子带图。分解滤波器与合成滤波器同样也需要满足Bezout恒等式：

图3　非下采样方向滤波器组

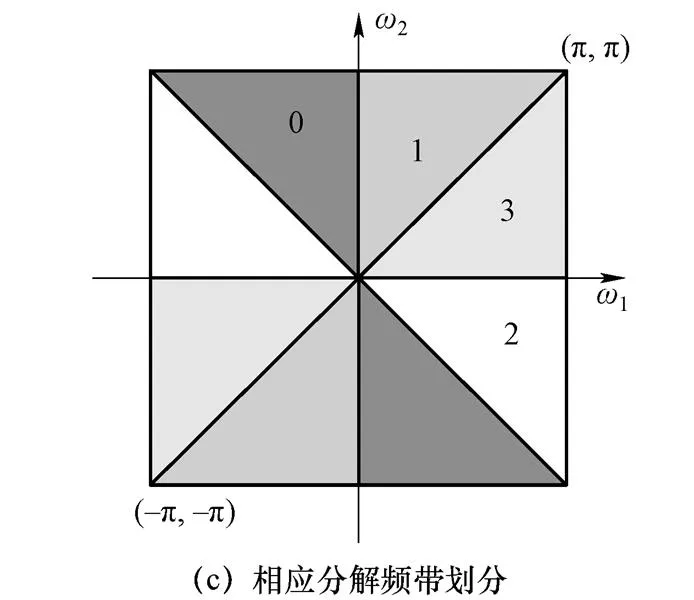
图3　非下采样方向滤波器组（续）

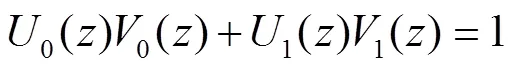
图4为图像进行3级NSCT分解的示意，每个尺度下的方向分解级数为2。首先采用NSP对源图像进行第一级分解，得到一个高频子带和一个低频子带，采用NSDFB对得到的高频子带进行多方向分解得到尺度一图像；采用NSP对第一级分解得到的低频子带进行第二级分解，同样可以得到一个高频子带和一个低频子带，以此类推，最终，NSCT将原图像分解为一个低通分量和若干高通分量。可以看出，NSCT分解有效地将图像的不同方向、不同频带信息进行了表示。

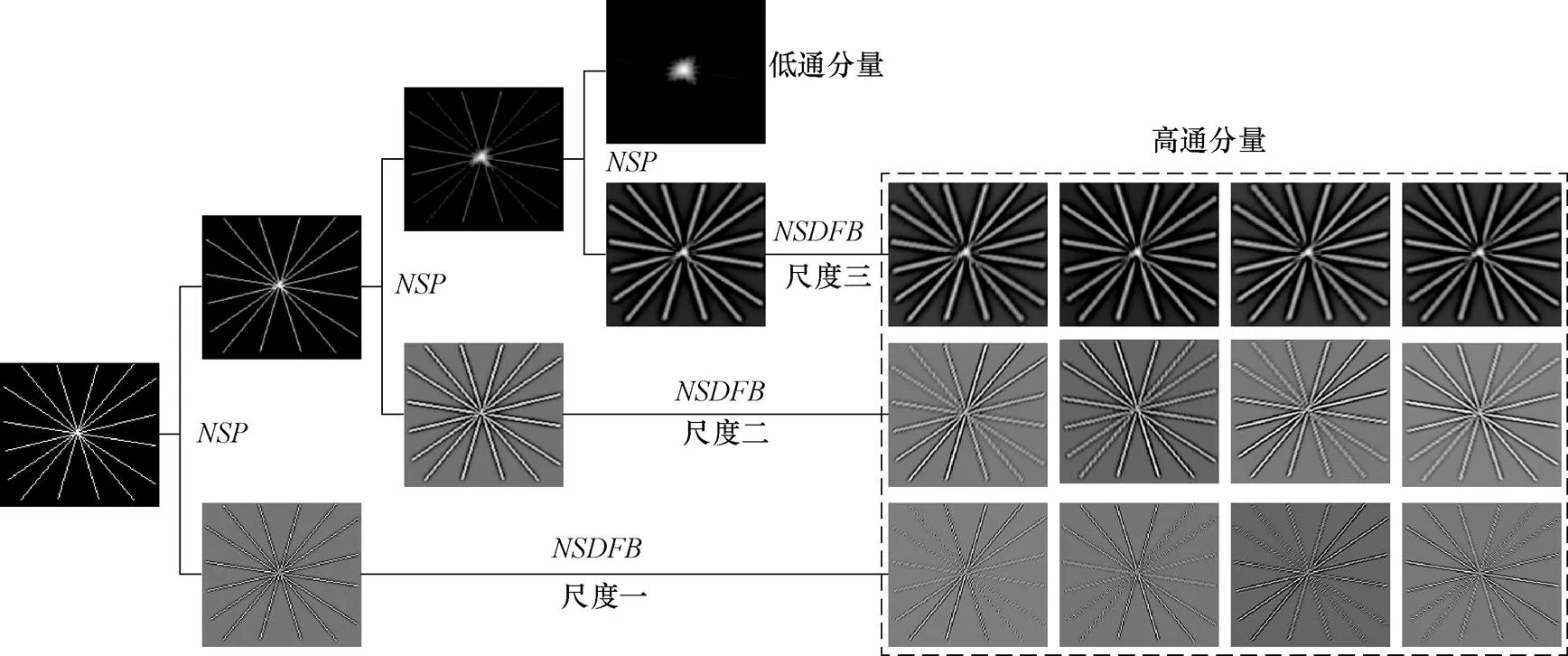
图4　NSCT多尺度分解图

1.2　简化的脉冲耦合神经网络

脉冲耦合神经网络（Pulse Coupled Neural Network，PCNN）[4,5]具有重要的生物学背景，被称为第三代人工神经网络。PCNN具有神经元的全局耦合和脉冲同步特性，与真实哺乳动物视觉皮层神经元较为相近，因此更加适合于视觉系统的描述，在图像处理领域中有着其他方法所不具备的优势。源图像经过NSCT多尺度、多方向分解后，各个分量的融合规则选择会极大地影响图像融合的质量。传统的加权平均等方法用于高频分量融合时会导致细节信息的丢失，不能达到很好的融合效果。PCNN具有位移、旋转、尺度和扭曲不变的特性，能够充分利用图像的全局特征，将其应用到图像融合中可以保留源图像的更多细节信息，获得显著的目标信息和较高的对比度。

原始的PCNN模型非常复杂，不便于实际的应用。在尽可能减少处理性能损失的前提下，PCNN模型应尽量简化，这样不仅能够提升处理效率，而且还方便实现。因此，简化的PCNN模型不断被提出，最常用的简化PCNN模型[6]如图5所示。

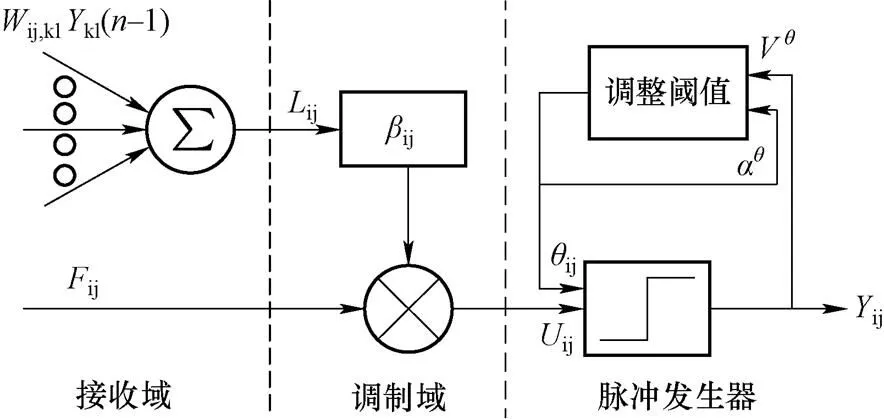
图5　简化的PCNN神经元模型[23]

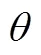
式中：——当前迭代次数；

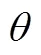
1.3　基于NSCT的图像融合算法设计

在图像融合的过程中，融合规则占有极其重要的地位。有效的融合规则能够明显提升图像质量，丰富图像所包含的细节信息。对于X射线与中子图像来说，其图像特点不同于同源图像，且中子与X射线的成像特性差异较大，轻元素对中子衰减较大，而金属材料对X射线衰减较大。图像上表现为金属材料在X射线DR图像亮度较低，而非金属材料在中子DR图像上亮度较低。因此，理想的融合图像需要将X射线图像中金属材料信息与中子图像中非金属材料信息进行融合，因此融合规则也需要进行相适应的选取。

图像低频子带系数主要展现的是图像灰度的概貌信息，常见的低频融合方法有简单取平均，绝对值取大以及区域能量最大化法等。X射线与中子图像融合，属于多源图像融合，在融合时直接取平均可以保留两幅图像低频基本的灰度信息，能够有效地将二者的金属材料及非金属材料的基本信息进行整合并体现在融合图像上，但是对于边缘处理不够精细，因此本文中，首先对输入的低频图像利用Sobel边缘检测算法进行边缘检测[7]。对于检测得到的图像1与2，其中对应边缘处灰度值为1，非边缘处为0，然后利用公式（4）对低频系数进行选择：

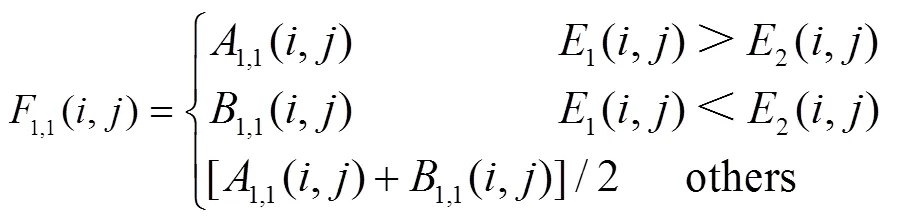
高频子带的系数表示了原始输入图像的细节信息和特征，如区域的边缘以及轮廓边界等，因此图像细节信息的丰富程度与高频子带系数直接相关。高频子带系数较大的，表示区域的对比度较大，图像更加清晰，所以在高频子带的融合规则中需要选取系数绝对值大者，可以将X射线图像中金属材料与中子图像中非金属材料的边缘、纹理等细节信息提取出来并融合。但是这样引入的问题就是当原始输入图像存在噪声时，由于噪声经过分解后的高频系数较大，导致融合后图像噪声问题仍然明显。尤其对于本文中的中子图像，受低中子产额以及成像过程中的γ射线的影响，往往信噪比较低，图像噪声水平相对X射线明显更高。因此，在高频子带的系数选择中，在相对低层的高频子带中使用绝对值取大融合规则，保证待融合图像中原有的细节信息不丢失，而在顶层高频子带中使用结合PCNN的融合规则，在选取系数时考虑周围像素点的影响，进而对中子图像噪声进行抑制。

（1）取大融合规则

取大融合规则本质上是选取两幅图像中系数相对较大、能量较高的系数作为最终图像对应高频子带的分解表示。其计算过程可由公式（5）表示：

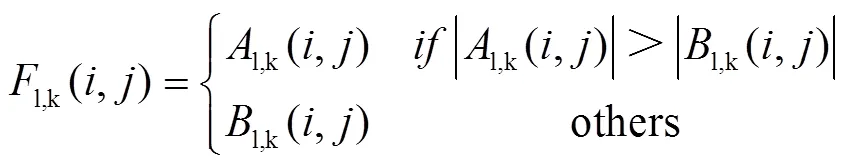
图像的特征信息是由邻域内的像素共同表示，而并非由单独的像素点表达，所以在融合时需要考虑具有较强相关性的邻域内像素的灰度值。拉普拉斯能量和可以很好地衡量图像中某邻域内图像灰度变化的相对值以及细节信息的丰富与否。拉普拉斯能量数学表达式如公式（6）所示。

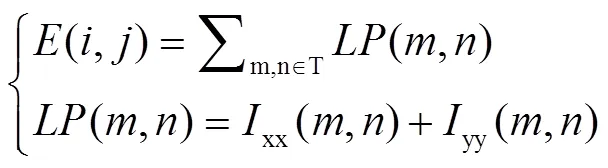
、——局部区域中心点的横纵坐标；

图像的能见度可以很好地衡量邻域内某点与整个区域平均灰度的关系，并判别该点是否为邻域内表现细节的点。图像能见度数学表达式如公式（7）所示。

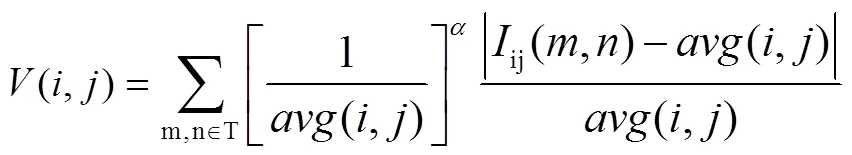
3.病理剖检。病死鸡剖析可见嗉囊充满积液，盲肠或小肠显著肿大，比正常肿大2～4倍，外表呈紫红色，肠腔充满凝固或新鲜的暗红色血液，盲肠壁变厚，浆膜层有针尖至米粒大小的灰白色糜烂点和紫色出血点间染，肠腔内充满许多混血内容物。

将拉普拉斯能量和与能见度作为PCNN算法的输入激励，在高频子带选取相对细节信息较为丰富的对应点的系数，其高频子带系数选择流程如下：

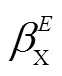
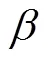
中子/X射线图像融合算法整体流程如图6所示。

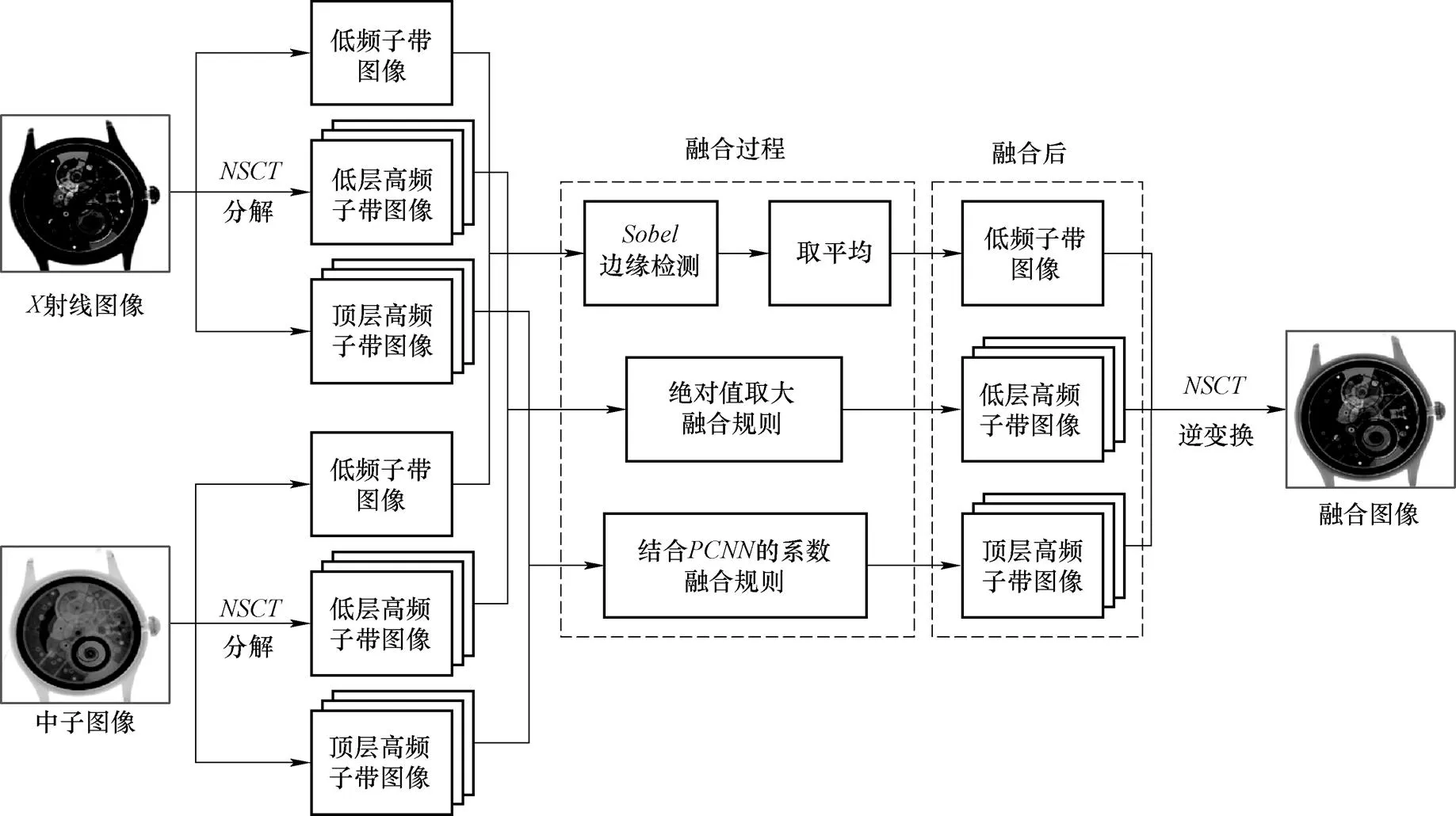
图6　X射线/中子图像融合整体算法流程图

详细的融合过程包括以下五个步骤：

Step1. 将已配准的X射线图像与中子图像进行NSCT分解，得到一个低频子带图像和一系列的高频子带图像；

Step2. 对两种模式下的低频子带图像分别执行Sobel边缘检测算法，并根据公式（4）对低频子带图像进行融合；

Step3. 根据公式（5）对低层高频子带图像进行融合；

Step4. 将两种模式下的顶层高频子带图像进行归一化处理并作为外部刺激输入PCNN，计算图像拉普拉斯能量和矩阵与能见度矩阵，然后将它们作为链接强度矩阵。通过简化的PCNN为顶层高频子带图像选择融合后的NSCT系数。PCNN融合过程如下：

2）根据公式（6）至公式（7）计算两种模式图像的拉普拉斯能量和矩阵与能见度矩阵并作为链接强度；

3）以图像归一化灰度矩阵作为外部刺激输入PCNN模型，根据公式（3）执行迭代步骤。

Step5. 通过NSCT逆变换重建得到融合图像。

本文所提出的方法由于将高频子带分为低层高频子带与顶层高频子带两部分，并分别采用不同的融合规则进行融合，所以在保留图像细节信息与保持图像对比度上有着较好的效果。同时由于顶层融合规则引入了PCNN系数，所提出的方法能够对图像噪声进行一定程度地抑制。

2　实验验证

为了验证本文所提出图像融合算法的有效性，我们选取结构较为复杂的石英表、机械表以及结构相对较为简单的U盘进行X射线与中子图像采集。X射线图像采集条件如表1所示。基于中国原子能科学研究院的热中子照相装置，我们实现了三种被检测样品的中子图像采集，中子采集条件如表2所示。

表1　X射线图像采集条件

表2　中子图像采集条件

图7所示为采集的中子与X射线DR图片，针对这三种样品的中子与X射线图像，本研究采用小波变换融合算法、拉普拉斯变换融合算法、传统的NSCT融合算法、NSCT-PCNN算法、Zhu等人的方法[8]以及本文所提出的算法对图像进行融合操作，图像融合结果如图8所示。

图7　中子与X射线图像

对图8融合结果中感兴趣区域进行放大，结果如图9所示。可以看出，Zhu等人的融合方法的凸显了边缘信息，但是实际样品中的同一物质体现在图中的灰度却并不一致，边缘处的梯度较大，整体主观视觉效果较差，这会影响对样品成分及结构信息的解读。同时，从图9（a）中可看出图像融合结果的细节丰富程度以本文算法最优，NSCT-PCNN次之，拉普拉斯算法，小波融合算法和NSCT融合算法的清晰度相对较差；在图9（b）中本文算法与NSCT-PCNN算法在保留图像细节方面更为优秀；从图9（c）中也可以看出本文算法融合效果明显优于其他算法。

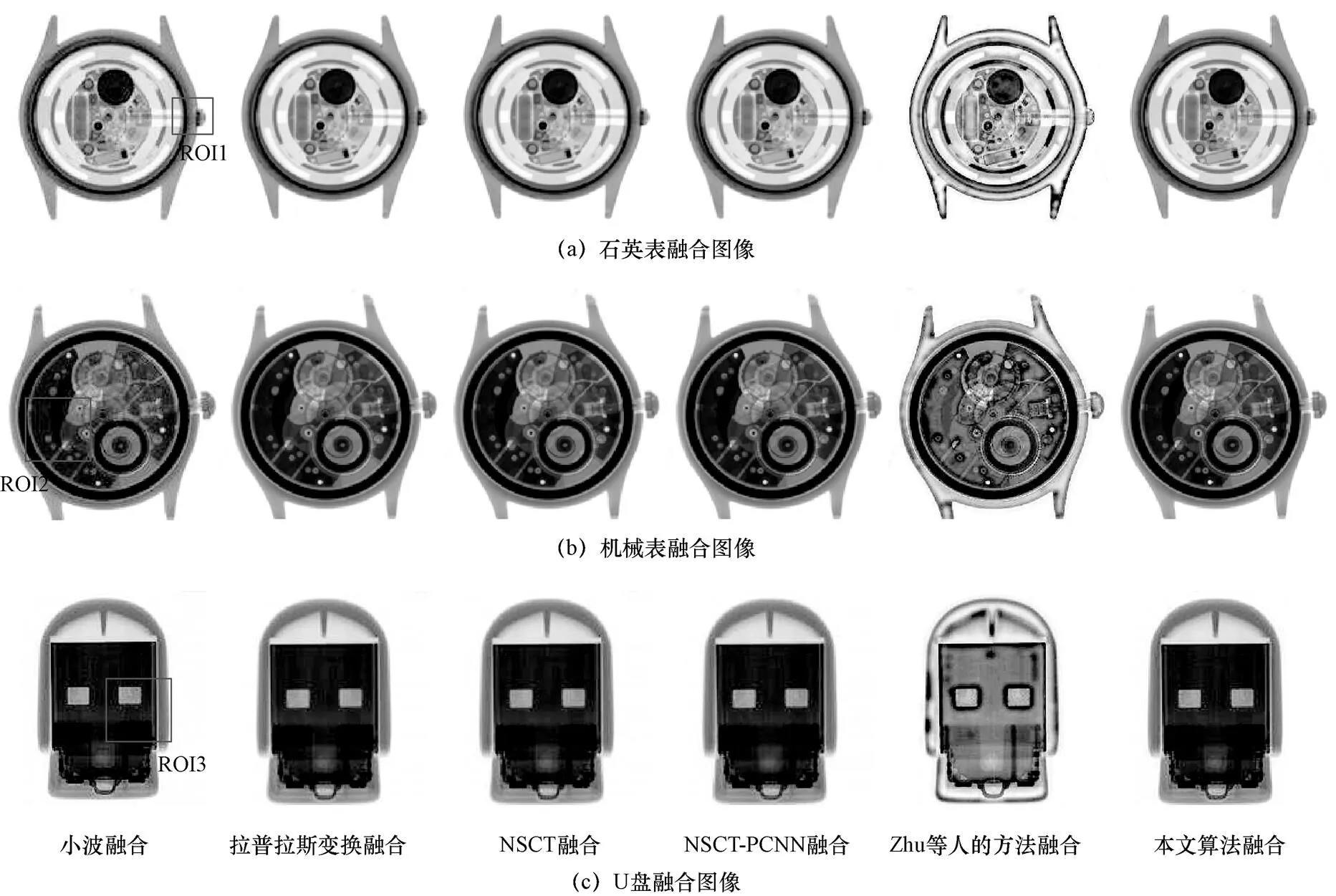
图8　中子与X射线图像融合结果

图9　融合图像细节放大图

本文选取峰值信噪比、平均梯度、信息熵[9]以及空间结构相似度[10]作为评价指标对小波变换、拉普拉斯变换、NSCT、NSCT-PCNN以及本文算法的图像融合质量进行客观评价，其定量结果对比如图10所示。

图10　融合结果比较

从图10中可以看出，本文算法除峰值信噪比相对于其他算法略低外，在平均梯度、信息熵以及空间结构相似度指标上均高于其他算法。其中，平均梯度以及空间结构相似度高于其他算法较多。

从实验结果中可以看出，所提出的算法在图像融合效果的主观评价与客观评价中均表现出优越性。相较于小波、拉普拉斯以及NSCT融合算法，本文算法与NSCT-PCNN算法的融合图像拥有更高的清晰度；相较于NSCT-PCNN融合算法，本文算法在细节处的表现更优，其对比度以及视觉效果更好。

本文算法能够有效地提取中子与X射线图像的特有的特征信息，在保证源图像细节信息不丢失的同时，可以将两种模式下的图像信息进行融合，并且在融合图像中展现。如图11所示。将配准后X射线、中子以及融合后的图像进行对比，对其中部分细节进行放大，从整体图与细节放大图中可以看到，在图11（a）中石英表的最外层边框、表把内杆以及内部下方电池的结构由X射线图像提供，而石英表中心结构到外壳之间的环状区域细节以及表把外部信息在中子图像得到展现；在图11（b）中，机械表中心及上方的齿轮细节由X射线图像提供，表把内部的内杆以及左侧内部的细节信息由中子图像体现；在图11（c）中，U盘方框内的细节部分在X射线图像得到展示，而下方细节则由中子图像提供。

图11　融合图像分析

3　结论

（1）为了保留待融合图像的整体特征，采用NSCT分解方法对中子和X射线图像进行了多尺度、多方向的分解，得到了一幅低频子带图像和一系列高频子带图像。

（2）为了得到更好地融合效果，针对分解图像的不同频带图像选择不同的融合规则。基于图像的边缘信息对低频子带图像进行取平均融合；对底层高频子带图像选取模极大值融合方法，而顶层高频子带则选取基于图像拉普拉斯能量和与能见度的PCNN算法进行系数选择。实验结果表明，融合后图像视觉效果更好。融合后的图像不仅有效融合了中子与X射线图像，而且很好地保留了二者丰富的纹理等细节信息。

（3）采用峰值信噪比、平均梯度、信息熵以及空间结构相似度作为评价指标对比了小波变换融合、拉普拉斯变换融合、NSCT融合与NSCT-PCNN融合以及本文算法的融合效果，结果表明，本文算法在图像细节信息丰富程度、图像对比度以及目标信息的融合方面均有着较好的表现。

本文所提出算法的主要目的是充分利用中子与X射线成像的互补特性，将这两种成像模式下的投影数据进行融合，从而克服彼此的成像弱点，得到被检样品更加精准、全面和直观的成像结果。针对不同的DR图像以及图像采集的条件，所提出的算法的融合参数应进行调整。同时，受采集条件所限，本文仅对DR图像进行了融合，并没有对中子/X射线的CT图像进行融合。因此融合参数的自适应调整以及中子/X射线CT图像的融合将是后续的重点研究工作。

［1］ STROBL M，MANKE I，KARDJILOV N，et al．Advances in neutron radiography and tomography［J］．Journal of Physics D：Applied Physics，2009，42（24）：243001．

［2］ YASUDA R，MATSUBAYASHI M，NAKATA M，et al．Application of neutron imaging plate and neutron CT methods on nuclear fuels and materials［J］．IEEE transactions on nuclear science，2005，52（1）：313-6．

［3］ 毛士艺，赵巍．多传感器图像融合技术综述［J］．北京航空航天大学学报，2002，28（05）：512-8．

［4］ IZHIKEVICH E M．Class 1 neural excitability，conventional synapses，weakly connected networks，and mathematical foundations of pulse-coupled models［J］．IEEE Transactions on Neural Networks，1999，10（3）：499-507．

［5］ IZHIKEVICH E M．Weakly pulse-coupled oscillators，FM interactions，synchronization，and oscillatory associative memory［J］．IEEE Transactions on Neural Networks，1999，10（3）：508-26．

［6］ 苗启广，王宝树．一种自适应PCNN多聚焦图像融合新方法［J］．电子与信息学报，2006，28（3）：466-470．

［7］ JOBSON D J，RAHMAN Z，WOODELL G A．A multiscale retinex for bridging the gap between color images and the human observation of scenes［J］．IEEE Transactions on Image Processing，1997，6（7）：965-76．

［8］ ZHU Z.，ZHENG M.，QI G.，et al．A Phase Congruency and Local Laplacian Energy Based Multi-Modality Medical Image Fusion Method in NSCT Domain［J］．IEEE Access，2019，7：20811-24．

［9］ 杨艳春，李娇，王阳萍．图像融合质量评价方法研究综述［J］．计算机科学与探索，2018，12（07）：1021-35．

［10］HAGHIGHAT M B A，AGHAGOLZADEH A，SEYEDARABI H．A non-reference image fusion metric based on mutual information of image features［J］．Computers & Electrical Engineering，2011，37（5）：744-56．

Neutron and X-ray Radiation Images Fusion Method Study Based on NSCT

HE Linfeng1，ZHANG Xiaomin2，WU Meimei1，LIN Qiang2，YUAN Shilei3，LIU Xiaoguang1，YANG Min2,*

（1. China Institute of Atomic Energy，Beijing 102413，China；2. Beijing University of Aeronautics and Astronautics，Beijing 100191，China；3. Henan Huatan Testing Technology Co.，Ltd，Zhengzhou of Henan Prov．450000，China）

Since thecharacteristics of neutron imaging and X-ray imaging are highly complementary，the fusion of digital radiography（DR）images of these two imaging modes can significantly enrich the information of image details．In this paper，a fusion algorithm of neutron image and X-ray image in nonsubsampled Contourlet transform（NSCT）domain based on simplified pulse coupled neural network（PCNN）is proposed．The proposed method decomposes the source image in multi-scale and multi-directional by NSCT，which effectively retains the information of each layer，so that the fusion image show good clarity and contrast．At the same time，in order to better retain the information of the source image，the different frequency bands of the image are fused by taking the average，taking the largest absolute value and the fusion rules combined with PCNN coefficients．We collect neutron and X-ray images for quartz watch and mechanical watch with complex structures and USB flash disk with simple structures．Then wavelet transform fusion，Laplace transform fusion，NSCT fusion，NSCT-PCNN fusion，Zhu’s method and the proposed method are used to fuse the neutron and X-ray images．The quality of fusion images of different methods is quantitatively evaluated by various objective evaluation indexes．The experimental results show that the fusion algorithm proposed in this paper can significantly improve the image fusion effect，obtain clear target information，improve the image contrast，while retaining rich detailed information，and is superior to other typical methods in objective evaluation criteria and visual effect．

Image fusion；Nonsubsampled Contourlet transform；Pulse coupled neural network；Neutron image；X-ray image

TL48

A

0258-0918（2021）03-0662-13

2021-03-24

国家自然科学基金项目资助（11675012）；国家重点研发计划资助（2017YFA040370X）；国家财政部稳定支持研究经费支持，（WDJC-2019-04）

贺林峰（1981—），男，湖南人，副研究员，博士，现主要从事中子成像方面研究

杨民，E-mail：minyang.ndt@buaa.edu.cn