高速铁路简支梁桥上轨道高低不平顺谱特征波长分析

刘潇潇 李帅 陈嵘 王源 汪鑫

1.西南交通大学土木工程学院，成都610031；2.西南交通大学高速铁路线路工程教育部重点实验室，成都610031；3.招商局重庆交通科研设计院有限公司，重庆400060

持久稳定的高平顺性是列车安全平稳运营的根本保障。我国高速铁路已经形成了以桥代路的建设特点［1］，高速铁路桥梁跨度普遍为32 m或24 m，桥上铺设板式无砟轨道。从轨检车检测到的不平顺中挖掘并分析桥梁与轨道的结构信息对高速铁路线路的养护维修具有指导意义。

轨道不平顺谱是目前轨道质量的主要评价指标之一，不仅能够体现轨道不平顺的波长和幅值信息，还能够揭示轨道随机不平顺中隐含的结构信息［1-2］。轨道几何不平顺的周期性特征通常与下部基础结构有关。文献［3-5］认为桥梁跨度与轨道高低不平顺波长存在近似关系，混凝土本身的收缩、徐变是桥梁区段周期性不平顺的主要原因。文献［6］认为桥梁下挠也是引起桥梁区段周期不平顺的原因之一。文献［7］认为路基区段周期不平顺波长与轨道板、底座板长度密切相关，但对于周期性轨道不平顺及不平顺功率谱密度峰值的原因没有作进一步解释与分析。本文通过计算某客运专线桥梁段的轨道高低不平顺功率谱，探讨高速铁路桥梁区段不平顺谱特征波长与下部桥梁结构、轨道板结构的映射规律，并结合动力学仿真与数值模拟对该映射规律进行验证。

1 轨道不平顺谱的计算分析

1.1 谱分析方法

既有轨检车测得的高低不平顺主要由轨道本身的静态不平顺和车辆动荷载导致的刚度不平顺两部分组成。两者共同表现为与路线里程相关的复杂随机过程［1-2］。

试验研究表明［1-2］，一般的轨道不平顺数据具备平稳性和正态性特征，因此可视为空间函数的平稳随机过程。平稳序列长度为N时，对于采样频率为1、均值为0的有限长度的实平稳序列｛x（m）｝，0≤m≤N-1，其傅里叶变换为

式中：ωn=nω0，即第n个频率ωn为基本频率ω0的n倍；A0、an、bn为展开式系数。

因此傅里叶展开的各频率为

式中：λ1，λ2，…，λn分别为ω1，ω2，…，ωn对应的波长。

1.2 桥梁段高低不平顺频谱分析

一客运专线共有25座特大桥，其中32 m简支梁桥跨（长32.6 m）达1 000多跨。桥上铺设CRTSⅠ型板式无砟轨道，轨道板布置见图1。由于单元板不允许跨越梁缝，32 m简支梁中间布设5块长4.962 m的轨道板，端头各设1块长3.685 m的轨道板；两轨道板之间设7 cm宽伸缩缝。简支梁梁缝宽10 cm。

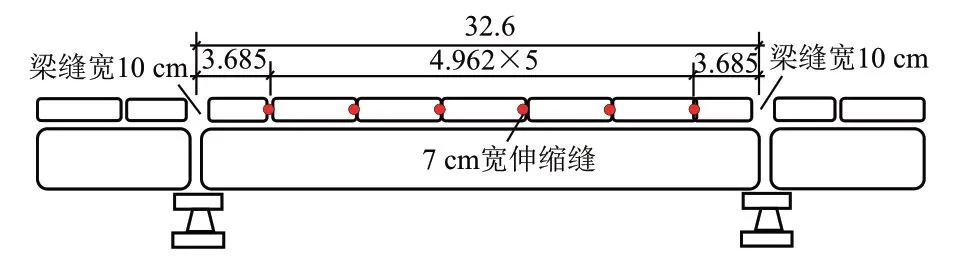
图1 32 m简支梁桥CRTSⅠ型轨道板布置（单位：m）

选取该客运专线上行线桥梁区段的轨检车数据进行研究。为尽可能减弱随机不平顺的干扰，采用周期图法以样本区段内各特大桥高低不平顺（4 096个数据点）来计算功率谱及密度值，再取其统计平均值，如图2所示。图中彩色曲线分别为25个特大桥区段的高低不平顺功率谱，黑色曲线为统计平均功率谱。从图2中提取典型峰值及其对应波长，见表1。

图2 特大桥高低不平顺功率谱峰值识别

表1 桥梁区段轨道谱峰值与波长

由表1可知，6个峰值所对应的波长满足近似的比例关系，即32.48∶16.47∶10.95∶5.45∶4.68∶2.52≈1∶1/2∶1/3∶1/6∶1/7∶1/13。结合式（5），波长比即频率反比。可见，频率比为近似整数关系。不平顺信号中的主要周期信号会以一系列尖峰的形式体现在其频谱上，且尖峰所对应的频率为该周期信号基本频率ω0的整数倍，即ω0，2ω0，3ω0，…，nω0。

由离散傅里叶特性可知，在高低不平顺谱中主要周期的每一个整分数波长处均应存在对应尖峰，但在图2中只直观得到6个尖峰值，在另外一些主要周期的整分数波长位置并未出现尖峰。究其原因，可能是因为随机因素的干扰而未能完全体现出来，或是统计过程中的误差导致部分尖峰出现的位置产生偏移。

由图2及表1还可以看出，随着特征波长的减小，其对应的谱密度值也减小，但在特征波长为5.45、4.68 m处存在较大谱密度尖峰值。结合该客运专线简支梁桥轨道板布设情况，认为突出的较大谱密度尖峰值是受桥上轨道板板长影响而产生的。

1.3 数值模拟验证

为研究轨道板板长与突出的较大谱密度尖峰值位置的关系，采用数值模拟方法，忽略其他因素的影响，取CRTSⅠ型板布置形式（参见图1），采用正弦函数分别模拟原始信号中桥长和轨道板长的周期信号，叠加得到模拟信号，如图3所示。桥长取32.6 m，轨道板长取（3.720+5.032×5+3.720）m。

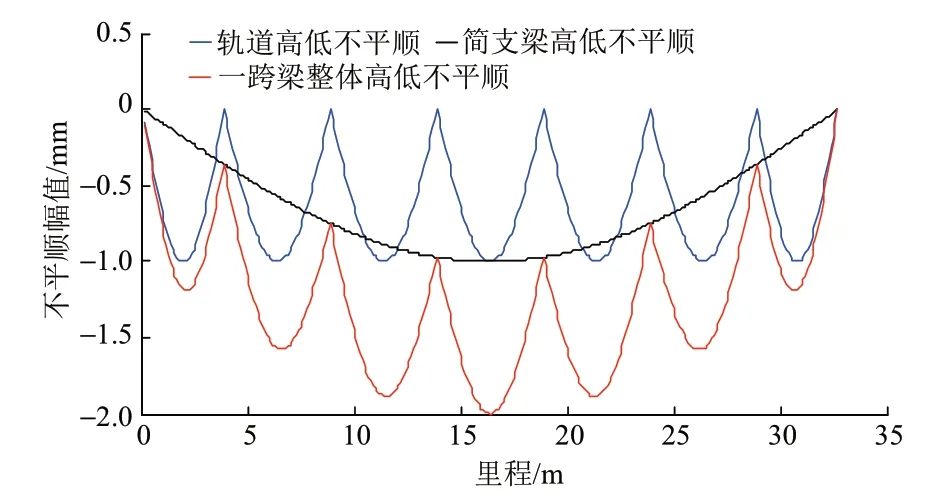
图3 单周期轨道高低不平顺模拟信号

复制图3中一个周期内的信号，得到一段3 km的信号，以模拟轨道周期不平顺。计算得到模拟信号的功率谱密度，如图4所示。从图4中提取突出的较大谱密度尖峰值所对应的特征波长，见表2。

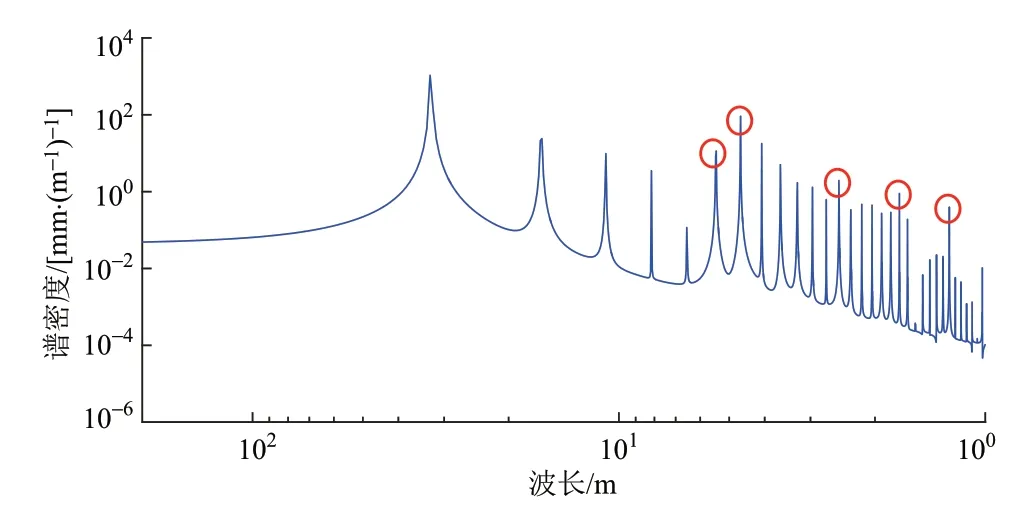
图4 数值模拟无砟轨道谱

由表2可知：5个峰值所对应的特征波长分别近似对应简支梁桥长（32.6 m）周期信号的1/6、1/7、1/13、1/19、1/26，而对于轨道板长度（5.032 m）周期信号，在其1/n处（5.03、2.52、1.68 m）处均不存在尖峰值。

由于与简支梁桥长（32.6 m）周期信号的1/6、1/7、1/13、1/19、1/26接近，在表2中的特征波长处出现较大谱密度值。次要周期接近主要周期的1/n，使主要周期在1/n及1/n之后即1/（n+1）、1/（n+2）等处的分量出现增益。此外，若次要周期的1/n接近主要周期的1/n，则主周期在1/n及1/n之后即1/（n+1）、1/（n+2）等处的分量也会出现一定增益。

表2 数值模拟谱的特征波长

2 动力学仿真分析

由于桥梁及轨道板结构引起的这种周期不平顺存在幅值增加的可能，因此，采用动力学仿真分析周期不平顺幅值变化对车辆动力响应的影响。

利用UM软件建立CRH动车模型，轨道不平顺采用波长32.6 m的高低正弦不平顺与以CRTSⅠ型板布置形式（参见图1）模拟的轨道板高低不平顺相叠加而得到复合周期不平顺。计算列车在该复合周期不平顺下的垂向加速度和轮重减载率，结果见图5。

图5 周期不平顺幅值对车辆动力响应的影响

由图5可知：①车体垂向加速度随着不平顺幅值上升而增大，且车速越大，车体垂向加速度越大。当车速超过250 km/h，随着幅值上升，垂向加速度增加幅度增大，在300 km/h时达到最大，但未超过安全标准。②轮重减载率与不平顺幅值、车速均呈正相关，当车速为120、160 km/h时，最大轮重减载率为0.34、0.52，未超过GB/T 5599—2019《机车车辆动力学性能评定和试验鉴定规范》［8］规定的容许限值；当车速为200、250、300 km/h时，轮重减载率分别在不平顺幅值为9、7、6 mm时超出容许限值，应立即采取维修措施，并持续监测不平顺幅值变化。

3 结论

本文采用周期图法计算某客运专线桥梁段高低不平顺功率谱密度，从频谱角度分析桥上不平顺谱特征，并结合动力学仿真与数值模拟的方法，探究轨道谱特征波长与下部结构的映射规律。主要结论如下：

1）在该客运专线桥梁段轨道高低不平顺谱中，32.48 m的主要周期不平顺与桥长有关；而在特征波长为5.45 m和4.68 m处的较大谱密度值与该客运专线采用的CRTSⅠ型轨道板长度有关。

2）在轨道结构中存在主要周期结构时，轨道高低不平顺谱中出现的尖峰大部分与该周期结构相关，其波长值满足1∶1/2∶…∶1/n的比例关系。

3）若存在主要周期结构，则次要周期结构仅仅影响主要周期结构所产生的谱密度尖峰值大小，不会在功率谱中产生独立的尖峰。

4）由动力学仿真结果可知，列车轮重减载率、垂向加速度与周期不平顺幅值、车速均呈正相关。轮重减载率在周期不平顺幅值达到6 mm时超出允许限值，应立即采取维修措施。