洞室爆破振动信号时频分析及能量分布研究

王子明， 闫建文， 杨振军

(西安理工大学 土木建筑工程学院， 陕西 西安 710048)

洞室爆破作为一种完成大量土石方开挖或抛填任务的爆破技术，一次性起爆药量较大，爆破段数较少，振动过程中会产生大量的能量，其引起的振动效应是影响爆破生产安全和边坡岩体稳定性的一个重要因素，故需对洞室爆破振动信号中携带的能量分布及爆破段数对能量分布的影响进行研究，而运用小波变换技术能较好地对振动信号各频带包含的能量值进行分析处理[1-6]。张耀平等[1]通过确定小波包层数，优选小波包基，运用MATLAB编程，得到能量的分布规律。晏俊伟等[2]为了深入研究爆破地震波特性, 应用小波变换方法对非平稳特点的爆破振动信号进行了能量分布特征分析。路亮等[3]结合应用实例，对实测信号进行多尺度的提升小波包分解后，得到了爆破振动各个频带的能量分布，总结了爆破振动信号频带能量的分布特征。杨智广等[4]采用理论分析与现场试验相结合的方法对爆破质点振速时程曲线进行EMD分解和Hilbert变换得出各频带的能量百分比以及总能量与距离的关系曲线。

学者们运用不同算法对振动信号的能量分布做了丰富的研究，但其研究对象多为小药量起爆产生的振动信号。而大洞室爆破起爆药量较大，振动信号包含的能量高，对洞室爆破的信号能量分布规律研究较少。在学者们对爆破振动信号研究的基础上，本文基于小波变换计算及Hilbert-Huang变换(HHT)方法，将二者对振动信号的时频分析优势相结合，运用MATLAB编写计算机语言，合理划分频段，计算洞室爆破引起的振动波各频段的能量及其主频的分布，对洞室爆破的振动信号的能量分布进行研究。并对比不同起爆段数对振动信号能量分布，并推论起爆段数对振动信号能量分布的作用规律。为实际工程提供一定的参考。

1 工程背景

1.1 工程概况

泉水沟尾矿库初期坝A标工程为堆石透水坝，由库内采石建坝，坝高84 m，坝顶高程为EL720 m，坝顶长度277 m，坝顶宽度为5 m，坝底左右宽度60～80 m，坝底上下游长度367 m，沟底纵向自然比降5.5%。根据初勘报告，坝体周边的风化安山岩完整性程度属破碎岩体，岩体基本质量等级为Ⅳ级；中风化安山岩，岩体完整性程度属较破碎岩体，岩体基本质量等级为Ⅲ级。

图1为施工场地全貌图，东北角标记处为尾矿坝坝体材料开采爆破区域及爆破方向。图1中心区域标记处为观测点布置区域。本次试验共进行两次起爆，各观测点距起爆点距离见表1。

图1 施工场地全貌图Fig.1 Overall view of construction site

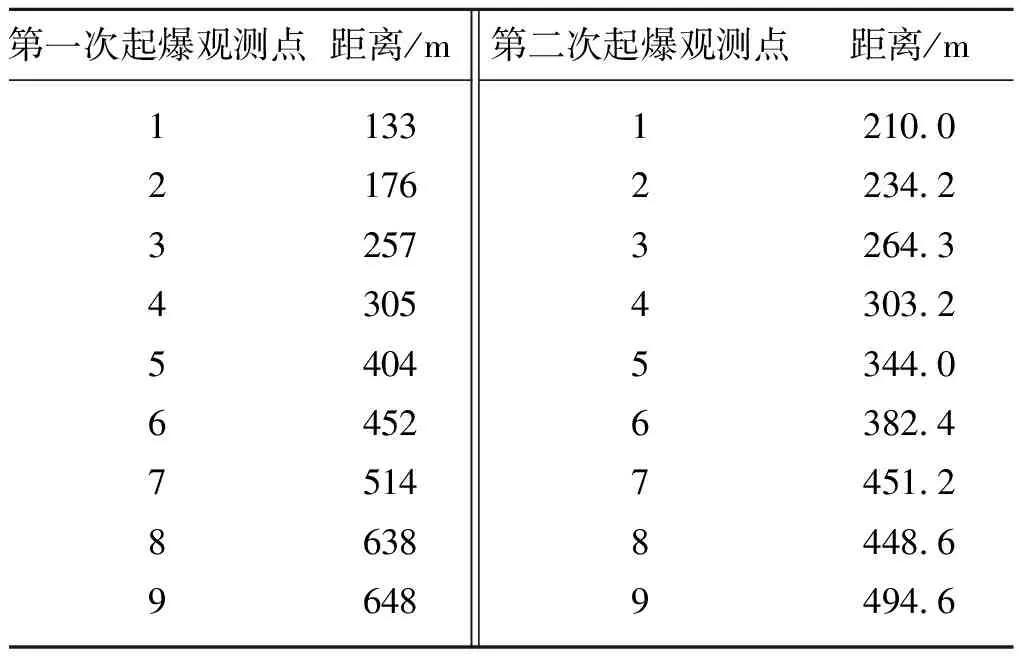
表1 观测点距起爆点距离

1.2 试验炮布置

第一次洞室爆破试验炮共六条药室，上层两条，下层四条，平均每段装药量12.6 t，装药总量76 t。试验炮起爆顺序为上层两条药室超前下层药室200 ms同时起爆，下层四条药室按100～150 ms的时差逐一起爆。第二次爆破试验炮共分9个装药段，前排5个，后排4个，平均每段装药量为9.5 t，最大单响装药量为12.4 t，最小单响装药量为2.67 t。调整后设计装药量为80.6 t，实际装药总量为80.2 t。

2 基于小波变换的信号分解

2.1 基本理论

设ψ(t)∈L2(R),其Fourier变换为ψ(ω)，当ψ(ω)满足允许条件时[7]：

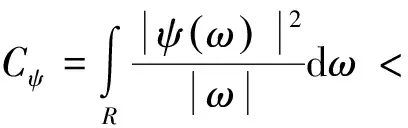
(1)

此时称ψ(t)为一个基本小波或母小波。将母函数经伸缩和平移后得：

(2)

称其为一个小波序列。式中a为伸缩因子，b为平移因子。对于任意的函数f(t)∈L2(R)的连续小波变换为：

(3)

其重构公式(逆变换)为：

(4)

由于基小波生成的小波在小波变换中对被分析的信号起着观测窗的作用，所以还应该满足一般函数的约束条件：

(5)

由于小波变换具有等距特性，即信号f(t)的小波变换是能量守恒的，根据内积定理(Moyal定理)，有下式成立：

(6)

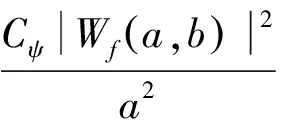
(7)

实际应用中,在多分辨率分析条件下,将爆破振动信号分解到不同的频率带上,通过离散小波变换的分层分解对不同频率范围内振动分量时间变化规律加以分析,从而给出爆破振动信号能量的时-频分布特征。采用二进小波时,函数f(t)满足如下分层分解关系：

f0(t)=f1(t)+g1(t)=…=
fN(t)+gN(t)+…+g1(t)

(8)

式中：fi(t)(i=1 , 2 ,…,N)表示函数分解出的低频部分，gi(t)(i=1 , 2 , … ,N)表示函数分解出的高频部分，下标表示对应的分解层次。当分析对象为爆破振动的时间历史x(t)时，有f0(t)=x(t)，于是式(8)可以简化为：

(9)

HHT法中EMD分解及Hibert变换的基本理论可参考文献[8],本文不再描述。

2.2 信号的采集及频段划分

本次爆破监测使用L20爆破振动智能监测仪，该仪器的采样频率为10 000 Hz，由Shannon定理得该信号的最大频率为500 Hz。爆破试验中，在爆区附近一条典型测线上及工程其他典型位置，共布置9个测点。实测三向振动波形见图2。

图2 实测三向振动信号波形图Fig.2 Waveform diagrams of the three-way vibration signal at the first observation point

在离散小波变换过程中，选取小波分解层数和小波基是关键。理论上分解可以无限制地进行下去，但事实上，分解可以进行到细节(高频)只包含单个样本为止。在实际应用中，一般依据信号的特征或者合适的标准来选择适当的分解层数,过高或过低的分解层数都不利于地震波信号的分析。当分解层数太低时，达不到精细化要求，分解层数太高又会造成信号失真的问题。由于信号的最大频率较高，且爆破振动的能量多集中在低频带区间(0～200 Hz)内，因此对原始信号进行8层分解，可得1～8级细节系数d1～d8及近似系数a8。其中1级细节系数d1代表最高频带，近似系数a8代表最低的频带，频带从d1到a8逐渐降低。再对各层近似系数进行重构，得到9个层次不同频带范围内的振动分布规律。由于版面原因，只给出第一观测点径向振动分量的各层重构波形图，波形见图3。

2.3 振动信号各频段能量分布计算

由于每组试验共设置9个振动观测点，每个观测点可收集径向、切向、垂向三组振动信号，故每组试验共收集27组振动信号。在MATLAB 2018a的编程环境下编写程序，对每个观测点所收集的信号进行小波分解及重构。计算第一观测点径向、切向、垂向三个方向振动分量的各频带能量值，其计算公式如下：

Ea=∑|Xa,k|2
(k=1,2,3,4,.....13 000)

(10)

式中：Ea为第a层频带的信号能量；Xa,k为重构信号第a层第k时刻离散点的振幅。对所有观测点原始信号进行小波分解并计算各层频带内产生的能量，同时对原始信号进行快速Fourier变换(FFT)，计算振动主频。其各频带振动信号的能量分布及主频结果见表2、表3和表4。

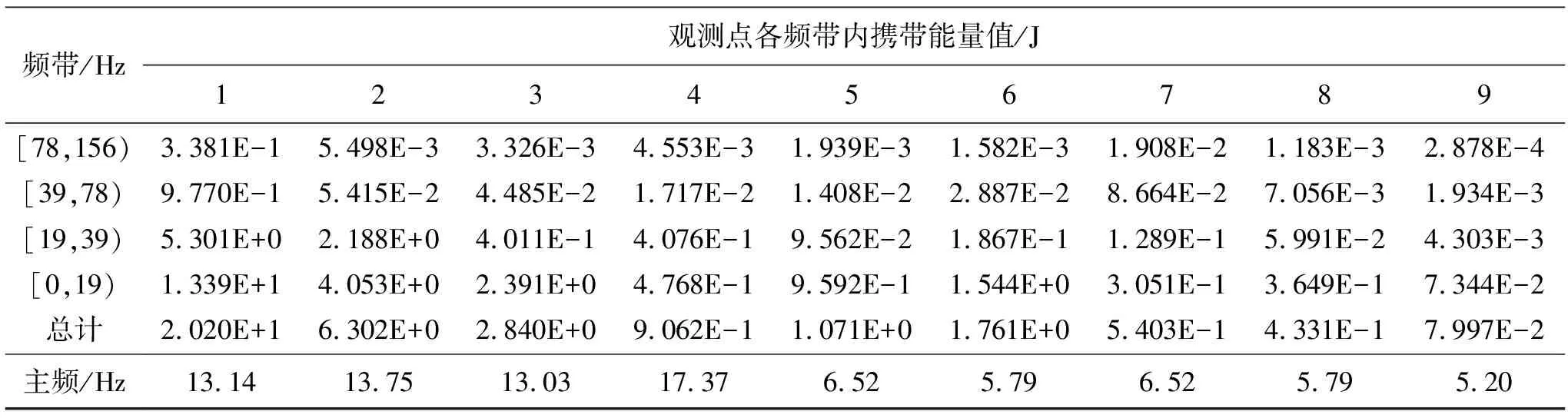
表2 径向振动分量能量分布Tab.2 Energy distribution of radial vibration component

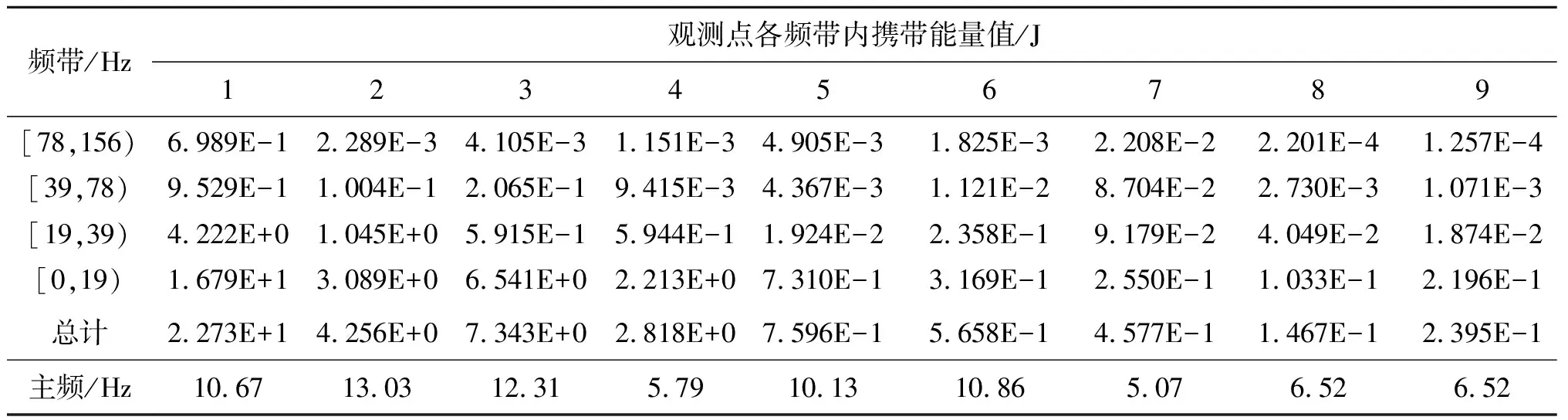
表3 切向振动分量能量分布Tab.3 Energy distribution of tangential vibration component

表4 垂向振动分量能量分布Tab.4 Energy distribution of vertical vibration component

结合参考文献[1]研究结果，爆破振动产生的的能量基本分布于低频带内，而大于200 Hz的频段所携带的能量微乎其微，故只列举[0,156) Hz频段范围内各频带的能量分布。对采样信号进行快速Fourier变换(FFT)，计算振动主频。由表2、表3和表4可知，试验9处观测点的径向振动分量在[0,39) Hz频带内的能量值分别占总能量的92.53%、99.03%、98.30%、97.60%、98.50%、98.27%、80.32%、98.10%、97.22%。切向振动分量在[0,39) Hz频带内的能量占比分别为92.45%、97.14%、97.13%、99.62%、98.77%、97.69%、75.78%、97.98%、99.50%。垂向分量相应为86.48%、98.13%、98.99%、99.06%、97.65%、89.85%、76.40%、98.55%、99.31%。在以上27组计算结果中，[0,39) Hz频段范围内携带能量占比达到90%以上的数据共22组，达到80%以上的共26组。结果表明爆破振动产生的能量基本处于低频率振动信号[0,39) Hz内，故大于156 Hz的高频率的重构信号所携带的能量基本可以忽略不计。

为便于表示各测点振动分量，各振动分量信号均用数字-字母形式表示(数字1，2，3…代表各个观测点，a、b、c分别代表径向、切向、垂向振动分量)。经计算得1-a主频为13.31 Hz，1-b主频为10.67 Hz，1-c主频为13.95 Hz。径向、切向振动主频均分布于振动信号携带能量最大的[0～19) Hz频段内，而垂向振动主频并不在其携带能量最大的[19,39) Hz频带区间内。主频的分布与携带能量最大的区间并不一致，因此计算9处观测点各向振动的主频分布，计算结果见表2、表3和表4。

由表2～4可知，第一组试验中27组数据的主频全部分布于[0,39) Hz频带内，径向、切向振动的主频分布区间为5～11 Hz，而垂向振动的主频分布区间为5～23 Hz。垂向振动的主频基本高于径向、切向振动主频，随着观测点距爆炸点距离的增加，径向、切向振动主频有逐渐减小的趋势，而垂向振动的主频与观测点距爆炸处距离的关系不明显。在以上27组数据中，只有1-c，7-c两组数据的主频未分布于其携带能量最大的区间内，因此主频基本能反映爆破振动能量比较集中的频带。但计算1-a，2-a，4-a，2-b，6-b，1-c，2-c，7-c振动信号[0,19) Hz与[19,39) Hz频带内包含能量的比值，1-a组[0,19) Hz包含能量为13.39 J，[19,39) Hz包含能量为5.301 J，两频带内包含能量比值为2.52。2-a组[0,19) Hz包含能量为4.053 J，[19,39) Hz包含能量为2.188 J，两频带内包含能量比值为1.85。依次计算其他组数据，4-a、2-b、6-b、1-c、2-c、7-c组两频带内包含能量比值分别为1.17、2.95、1.34、0.72、1.71、0.62。由以上计算结果可知，在[0,39) Hz频段范围内，虽然主频所处的频带包含的能量值最高，但其相邻的子频带内亦携带大量的能量，1-c、7-c相邻子频带所携带的能量甚至超过了主频所处的频带。以上8组数据中，相邻的子频带所携带的能量占主频带携带能量值的33.9%～161.9%，由此可见很多情况会出现几个频带能量集中的现象，这些频带内所包含的能量与主振频率所在的频带包含的能量相当，有时甚至比主振频率所在的频带能量还多，导致爆破振动信号出现多个峰值。通过小波能量分析及快速Fourier变换法，主振频率基本落在能量集中的频带，说明用主振频率来衡量爆破振动的安全性是可靠的。但能量在各频带均有分布，虽大多集中在主振频率附近，但很多情况都会出现几个频带能量集中的现象，这说明爆破振动安全标准中仅用Fourier变换计算主振频率的方法尚不够完善。

2.4 不同装药段数对爆破能量分布影响分析

第二次爆破试验的装药情况为：本次共分9个装药段，前排5个，后排4个，平均每段装药量为9.5 t，最大单响装药量为12.4 t，最小单响装药量为2.67 t。调整后设计装药量为80.6 t，实际装药总量为80.2 t。

对比第一次爆破测试装药量，本次起爆的装药量总量为80.2 t，与第一次的76 t装药总量相近。不同于第一次装药结构，本次试验采用9段微差爆破起爆网络结构。试验同样沿起爆点每隔一定距离布设一个振动观测点，共布设9个，其中每个观测点距起爆点的距离与第一次起爆近似。本次试验共9个振动观测点，观测点位置与距起爆点距离与第一次起爆相同。每个观测点可收集径向、切向、垂向三组振动信号。全试验共收集27组振动信号。对所有观测点原始信号进行小波分解并计算各层频带内产生的能量。其各频带振动信号能量分布与主频结果见表5、表6和表7所示。

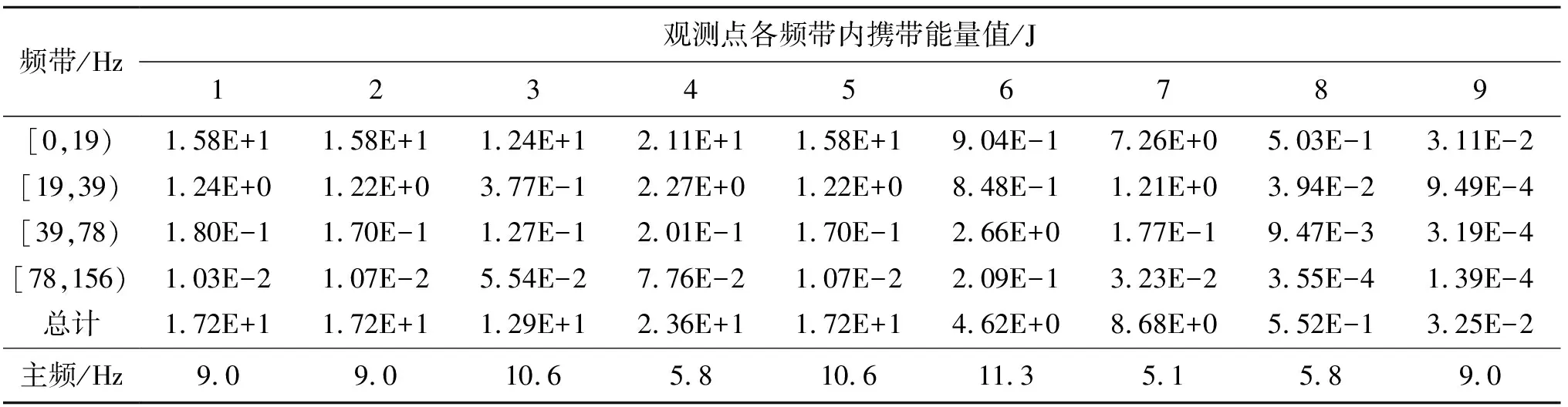
表5 第二次振动监测径向振动分量能量分布及主频Tab.5 Energy distribution and main frequency of radial vibration component in the second vibration monitoring

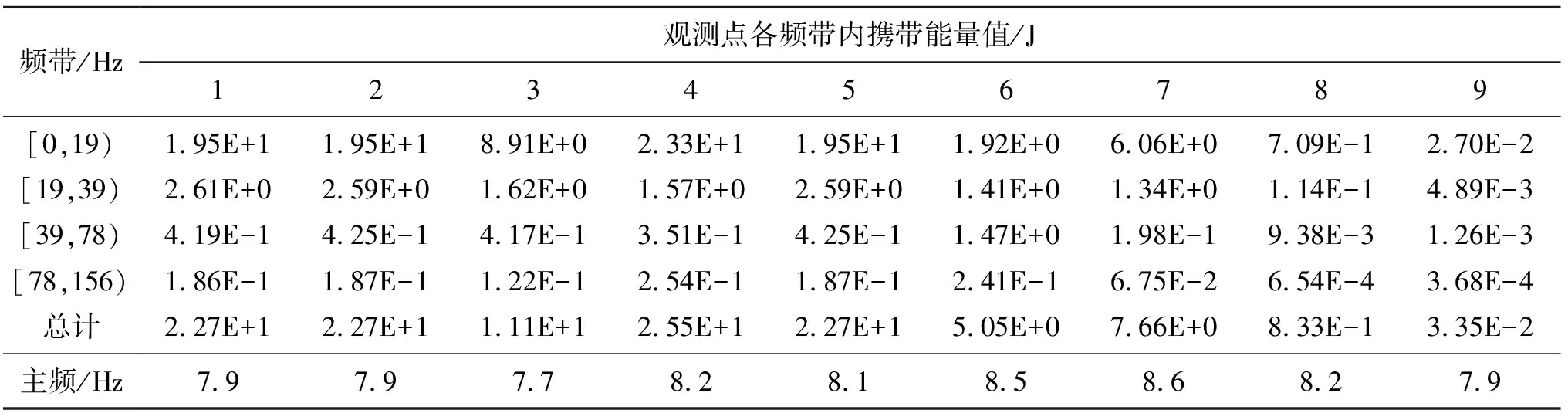
表6 第二次振动监测切向振动分量能量分布及主频

表7 第二次振动监测垂向振动分量能量分布及主频Tab.7 Energy distribution and main frequency of vertical vibration component in the second vibration monitoring

由表5、表6和表7可知，由于起爆方式的变化，主频分布越加密集并且频率较低，27组数据中主频全部位于[0,19) Hz频段范围内。在以上27组计算结果可知，[0,19) Hz频段范围内携带能量值占全部能量的比值最大，爆破所产生的能量基本都位于[0,19) Hz频带内，故主振频率亦基本落在能量集中的频带[0,19 Hz)。计算27组数据[0,39) Hz频带范围内能量分布占总能量的比值，其中能量占总比达到90%以上的共23组。结果表明随着起爆段数的增加，爆破主振频率越向低频区间集中，爆破产生的能量有向低频带内集中分布的趋势，且产生的能量基本分布于[0,19) Hz频带范围内。主振频率分布区间与携带能量最大的频带基本相一致。与第一次爆破监测相比，随着起爆段数的增加，同时存在几个频带能量集中的现象有所减少。

2.5 基于HHT的不同段数能量分布对比

Hilbert-Huang变换(HHT法)可以同时从时域(持续时间)和频域(主振频带)角度反映爆破振动信号能量的变化及其分布规律，故运用HHT法对振动信号进行时频分析。为减小观测点与爆源的距离对能量分布的影响，从两组实验中各选取第三点处(距爆源距离分别为257 m、264 m)收集的振动信号径向分量对比分析。经EMD分解后再进行Hilbert变换，可得两振动信号径向分量的三维时频谱图，见图4。

图4 振动信号三维时频谱图Fig.4 Three dimensional time-frequency spectrum of vibration signal

从频域的角度分析，两次试验中能量均基本分布于低频段内，0～50 Hz内能量分布最为集中，与上节分析结果相一致。由于第一次试验装药段数少于第二次试验，其振动能量多集中于0.5 s之前，而第二次试验由于装药段数的增加，瞬时能量在时域上分布较为均匀，不同起爆段波形的相互叠加削弱的作用更为明显，第二次试验中瞬时能量的最大值较前者亦有所下降。从图4中无法看出信号的主振频率，但由图4(a)可以看出，在段数少的情况下，信号在频域上分布于低频段内，在时域上也集中分布在某一时段。由于不同段爆破形成振动波的相位不同，使叠加信号形成新的波峰或波谷，在段数较少的情况下主频主要受微差间隔时间的影响，段数对主频的影响较小。由图4(b)可以看出，随着爆破段数的增多，其形成的振动波也因此增多，振动波间相互叠加的作用效果也有所提升，同时信号在高频区段分布较前者也有所增加。因此推论由于爆破段数的加大，其对主频的影响增加，产生的振动波的叠加作用效果更为明显，同时振动波的叠加部分不仅仅集中在低频的主振频率附近，高频部分之间亦相互叠加，由于振动信号的相互叠加的振幅削减作用，高频信号的振幅相应减小，从而使信号主频向低频段收敛。

3 结 论

1) 洞室爆破工程中，爆破振动信号在三个方向(径向、切向、轴向)上产生的能量基本处于低频段(0～39 Hz)，其包含能量占总能量的比值高达90%以上，而156 Hz以上频带所包含的能量占总比不足0.01%。故振动信号携带的能量多集中在低频段区间内。

2) 通过小波能量分析及快速Fourier变换法，主振频率基本落在能量集中的频带，说明用主振频率来衡量爆破振动的安全性是可靠的。但能量在各频带均有分布，虽大多集中在主振频率附近，但很多情况都会出现几个频带能量集中的现象，这说明爆破振动安全标准中仅用Fourier变换计算主振频率的方法尚不够完善。

3) 增加起爆段数，能使爆破主振频率分布区间与携带能量最大的频带基本趋于一致，同时存在几个频带能量集中的现象有所减少。结合HHT时频谱图推论，由于爆破段数增加，更多振动波参与叠加，高频段振动分量相互叠加振幅消减，从而使主频向低频率收敛，对主频作用更为明显。