基于连续性损伤理论对P91钢蠕变的损伤研究

邢迪雄，王洪洲，王进峰，丁海民

（1.华北电力大学机械工程系，河北保定071003；2.华北电力大学工程训练中心，河北保定071003）

P91钢是高温承压部件的常见钢种，广泛地应用在火电厂发电、航空航天、化工工业等严酷的环境中。P91钢是在9Cr-1Mo钢基础上通过添加V、Nb和N元素得到的，具有比P22钢更优良的抗蠕变能力和高温强度，火电厂超（超）临界机组一般应用P91钢作为主蒸汽管道、高温再热器、过热器用钢等。

P91钢是一种新型的马氏体耐热钢，长期在高温高压的环境下服役，蠕变现象不可忽略。国内外的学者对蠕变开展了大量研究，一直无法给出精确的数学物理描述来阐述蠕变现象。损伤理论通过描述材料内部的损伤情况从而对构件进行评估，一般用损伤变量D表征材料的受损情况。Ogata等［1］对带有焊件的P91钢管进行了单轴和多轴蠕变下损伤特性的研究，同时应用损伤理论的方法对纵向焊管试样进行三维有限元蠕变分析，确定了试样的内应力和蠕变应变的分布，得到了蠕变间隙对蠕变损伤的影响。Guguloth等［2］对改性的9Cr-1Mo钢运用损伤理论描述了蠕变行为并且对微观结构演变进行了研究，通过扫描电子显微镜研究破裂试样的断裂表面形态，进一步阐明了蠕变破坏机制。Jing等［3］提出了一种基于连续介质损伤力学的蠕变-疲劳裂纹扩展模型，并对P91钢试样在625℃下裂纹扩展进行了数值分析，其结果与实验结果相一致。Sakai等［4］提出应用空洞生长的模型模拟P91钢焊管内压蠕变损伤，表征了纵向焊接管热影响区（Heat Affected Zone，HAZ）中蠕变损坏的演变过程，建议采用损伤的方法评估蠕变实验下HAZ中的蠕变损伤分布。Hyde等［5］利用单轴和缺口棒蠕变实验数据建立了P91钢的材料损伤行为模型，使用P91管道的这些材料特性进行有限元分析，获得了管道的失效寿命并在蠕变损坏条件下进行高温部件失效预测的初步评估。

国内研究P91钢蠕变损伤起步较晚，但是也取得了一些成果。张斌［6］和涂善东等［7］对P91钢的发展过程以及蠕变断裂寿命的关键问题进行了阐述，分析了材料、组织结构、本构模型等对蠕变损伤的影响。何晓东等［8］对P91管样进行了持久性能实验，采用金相、扫描电镜和X射线能谱分析对P91钢试样进行蠕变损伤的研究。束国刚等［9］利用损伤理论的方法对P91钢试样标准件进行有限元分析。陈云翔等［10］在600℃温度下应用CDM模型模拟T/P91钢的蠕变损伤行为。张国栋等［11］考虑了焊接接头的残余应力，对焊件进行了蠕变模拟，得出蠕变损伤较大程度地受焊接残余应力的影响，蠕变损伤与焊接残余应力的分布区域基本一致。

1 损伤理论

1958年，苏联学者Kachanov［12］采用引入连续性因子的场变量Ψ来描述材料劣化的综合效应。此后，如Hult［13］、Murakami等［14］为损伤理论的建立作出了重要的贡献。蠕变损伤是在蠕变情形下发生的材料不可逆损伤。金属一般在高温恒载的环境中，随着时间的积累，金属的黏塑性就会产生延时变形。在材料损伤过程中，内部的晶格会产生畸变，晶格间会发生位错和滑移。在蠕变损伤的后期，在晶格和晶界间甚至会穿晶产生微裂纹和微空洞使材料的耐久性迅速下降，对核心部件的寿命将产生重要的影响。一般的蠕变损伤模型表示为

式中：D为损伤变量；Y为损伤耗能率为初始截面积；α0为材料参数；E为杨氏弹性模量；σ*为标识应力。

一般认为，损伤出现在蠕变的第3阶段，这一阶段很难计算出累积塑性应变率̇，因此，应用Odgvist定律，将和应力建立如下关系：

联立式（1）、式（2）和式（3）可得

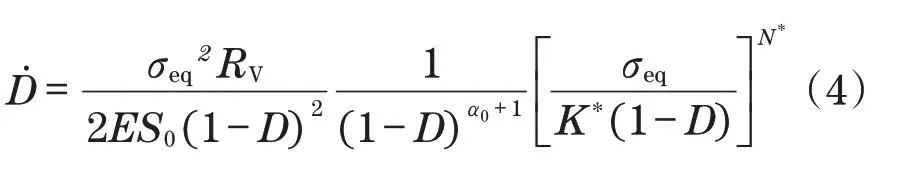
式中：σeq为等效应力为材料参数。

为使公式进一步简化，作如下处理，定义r=N*+2，α3=α0+N*+3，Ar=2ES0K*N*，式（4）变为

当一维拉伸时，有RV=1，σeq=σ，则

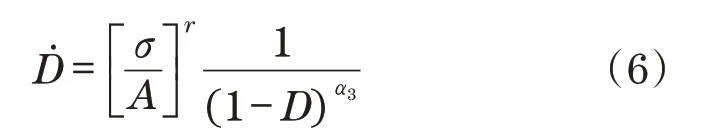
式中：A、α3、r为材料参数。

损伤的测量一般是比较困难的，在实际情况下，一般利用第2阶段蠕变时应用应变等效原理得到的耦合损伤蠕变方程间接测算损伤。

2 实验及参数的确定

实验材料为未经服役的P91钢管沿管道纵向取材加工成直径为10 mm的棒状标准蠕变件，实验温度为620℃，实验应力为145、155、164 MPa。实验设备采用RDL50电子蠕变实验机，实验规程参照国家标准GB/T 2039—1997进行。

从图1中可以明显看出，蠕变分为3个阶段，其中，蠕变稳态阶段占整个寿命周期比重最大，时间也最长。蠕变3个阶段可做如下解释：在蠕变的第1阶段，随着载荷的突然加载，材料产生了大量的位错并出现滑移运动，产生快速变形，随着应变硬化而减速；在蠕变的第2阶段，可解释为应变硬化和损伤软化相平衡，即产生位错等缺陷而强化和位错等缺陷消失而软化的速率相等，造成了几乎不变的蠕变速率；蠕变的第3阶段主要由断裂机制控制，材料内部和外部的损伤开始起作用，材料内也开始出现微孔洞和微裂纹，打破了第2阶段所保持的平衡，出现了蠕变速率迅速增加的第3阶段。

图1 蠕变曲线Fig.1 Creep curve

经理论分析，从实验数据可以得到损伤模型的参数，带入可得损伤模型表示如下：

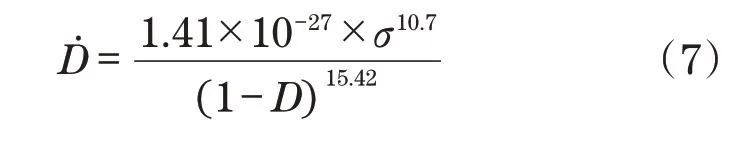
3 应力及蠕变对实验损伤的影响

图2是620℃温度、应力为164 MPa下P91钢的损伤曲线。如图所示，损伤在一定范围内波动，断裂损伤为0.47，并没有达到理论计算损伤值为1的破断损伤。大量实现数据表明，蠕变损伤值在0.15～0.85之间［15-16］。图3为寿命分数与损伤关系曲线。由图可知：随着应力的增大损伤也随之增加，损伤增加速度也随着应力的增加而加大；破断损伤相差不大，破断损伤一般与材料的特性有关，与时间、温度关系不明显。图4～图6为损伤曲线与损伤模型的拟合，从图中可以看出，损伤模型可以描述蠕变的3个阶段，并且损伤模型损伤值可以达到1，破断损伤存在突变，对拟合效果无影响。

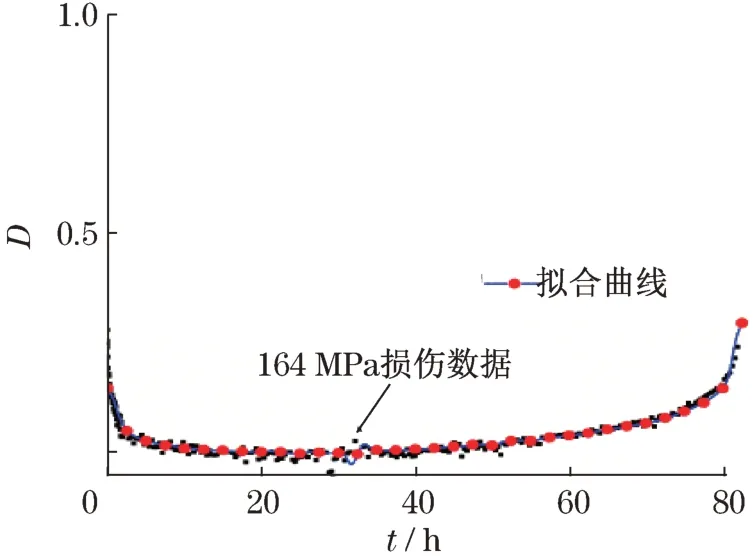
图2 164 MPa损伤Fig.2 164 MPa damage

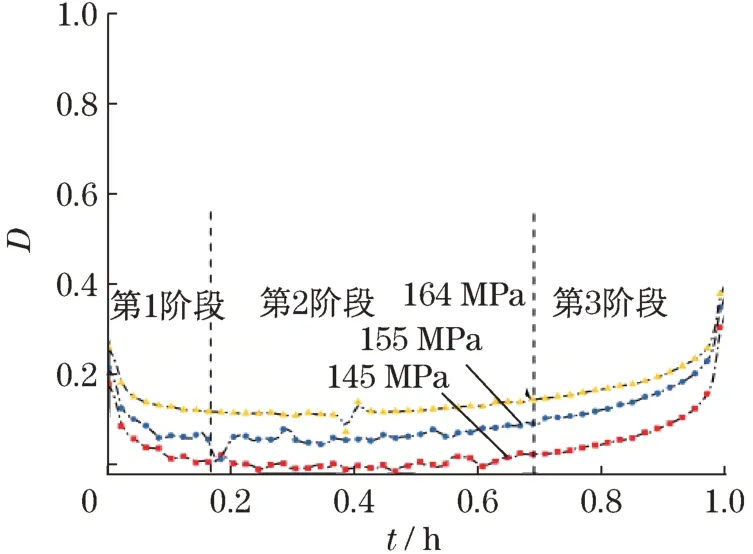
图3 寿命分数对损伤的影响Fig.3 The effect of life fraction on damage

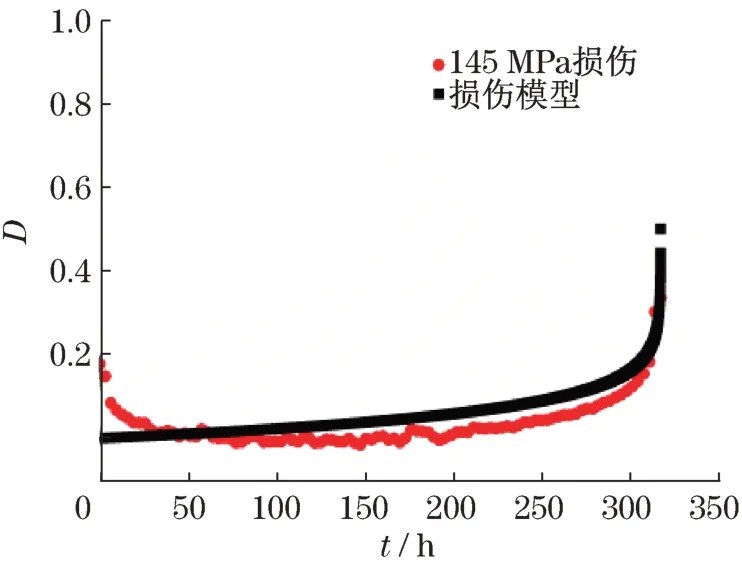
图4 145 MPa损伤拟合曲线Fig.4 145 MPa damage fitting curve

图5 155 MPa损伤拟合曲线Fig.5 155 MPa damage fitting curve

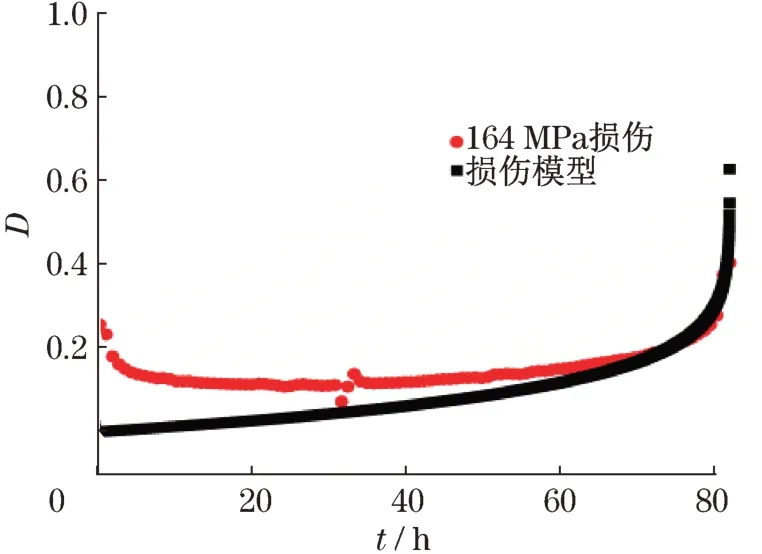
图6 164 MPa损伤拟合曲线图Fig.6 164 MPa damage fitting curve

图7为蠕变对损伤的影响曲线，理论认为蠕变的第1、第2阶段损伤为0，损伤开始于蠕变的第3阶段。实际测试得到的损伤，由于蠕变第1阶段的蠕变率要大于第2阶段，故曲线一开始就存在损伤且随时间逐渐减小。蠕变第2阶段由于数据的不稳定性，会产生小范围波动，如图7所示。当到达蠕变的第3阶段时，损伤量随着蠕变的增加而增加，几乎呈线性增加。在同温、同变形下，随着应力的增大，损伤量也略有增加。

图7 蠕变对损伤的影响Fig.7 Impact of creep on damage

4 结论

（1）根据620℃温度和外载荷为145、155、164 MPa下P91钢材料的蠕变损伤数据，利用连续性损伤理论推导出材料的损伤方程，并进行数据的拟合，损伤理论可以完整地描述蠕变过程，拟合效果较好，证明了损伤理论描述材料蠕变的准确性和完整性。

（2）理论上P91钢材料在蠕变的第1、2阶段损伤值为0，破断损伤为1，但在实验测试下，P91钢材料由于蠕变第1阶段的蠕变率大于第2阶段，造成第1、2阶段的损伤不为0，并且破断损伤小于1。

（3）同温下，在损伤开始阶段，蠕变和材料损伤呈线性关系，损伤随着应力的增加而增加；基于连续性损伤理论，推导出620℃温度下P91钢损伤参数，可以为寿命评估提供一定的指导。