基于NURBS的光学镜片重构算法研究

韩世凡，付东翔

(上海理工大学 光电信息与计算机工程学院,上海 200093)

渐进多焦点镜片能够为近视或远视患者提供连续清晰的视觉，给配戴者带来舒适的体验，因此得到了广泛的应用。随着渐进多焦点镜片和自由曲面技术的发展，设计渐进片变得日益重要[1]。在光学渐进镜片设计实验中，用光学计算出的渐进镜片总是表现出不必要的侧向散光和聚集误差，镜片表现出歪斜变形。因此，研究者试图将插值曲面用于已知曲面的形状表示光学镜片。在已知曲面型值点的情况下，尝试用多项式插值和有效最小二乘法逼近，但计算结果的精度较差，不能够有效地表达曲面的特性。基于Non-Uniform Rational B-Spline(NU-RBS)的技术具有精确表达曲面的特点，能够在一般和特殊曲面之间的组合中展现其优秀的描述能力，而且通过修改控制点和权值能够对界定面积曲面修改，具有重要的学术和应用意义。在镜片曲面设计过程中，若要得到理想的镜片形状，需要不断地进行调整，但设计人员直接考虑的是曲面的大致形状，而非控制网格的形状。因此实际操作中需要利用反算得到初始控制点，从而一步一步修改得到理想的曲面。曲面重构理论和技术在现代工业、信息产业、数字媒体业等领域有着广泛的应用，受到学者的广泛关注。20世纪80 年代中期，文献[2]首次提出了散乱点云网格重建问题，通过边界点的三维坐标来提取曲面特征。文献[3]提出将散乱数据点参数化为B样条拟合所需要的四边形网格，再用距离函数控制拟合误差。文献[4]通过已知测地线的参数曲面束，反算出所需曲面。文献[5]则对逆向过程得到的曲面保持光顺性进行了研究[5]。

本文提出利用修正弦长法将镜片上的点进行参数化，再用NURBS反算算法得到控制点，从而得到用NURBS表示的曲面。然后通过修改控制点与权值，进行曲面的局部修改，并通过FFV仿真软件和MATLAB对光学参数分析以判断镜片是否达到设计要求。

1 数据处理

1.1 渐进片介绍与型值点选取

因为渐进多焦点镜片的光焦度具有自上而下渐变的特点，表面不具有回转对称性，所以表现为空间自由曲面[6]。渐进多焦点镜片在上为远视区，在下为近视区，连接两个区的渐变区为通道，通道上度数渐变。渐进镜片如图1所示。

图1 渐进镜片图Figure 1.Progressive lenses

在曲面重建之前，必须找到合适的型值点。对于这些散乱的数据点，需要进行优化处理，去除掉重复的点，得到一个较好的数据模型。因为镜片是自由曲面，对于镜片上的矢高等于曲面的型值点，可利用渐进片矢高计算专利[7]来得到曲面上的点。矢高是用来镜片中表现弯曲程度的量，当曲面上所有点所对应的弦都在一个面内，可以通过计算来得到渐进片上的矢高获得型值点。对于型值点，只知道它的空间坐标值，故可将其看做点云数据。若要让点按照一定的拓补结构进行排序，首先需要将点云数据按照八叉树结构进行存储，确定每个点的k近邻。初始曲面边缘的区域作为初始区域，按照迁至约束和综合优化准则进行控制，每个点都有邻域，构造一个种子四角形。从初始区域开始，向曲率变平稳的区域移动，点云数据按照一定拓扑结构排列[8]。

1.2 数据平滑

噪声点的出现会对控制多边形产生影响，从而影响重构出来的曲面。如果将点云数据直接进行曲面重建，噪声点的出现可能导致出现局部曲率变化大的问题，在后期进行曲面重建的过程中易造成曲面光滑度不够，增加曲面重构计算负担。因此，需要进行平滑处理，去除噪声点。点云数据由大量的型值点构成，而噪声点可以认为是一种高频的随机采样点，大量随机变量服从或近似正态分布。所以，本文使用高斯滤波来进行平滑处理，通过高斯滤波器在指定域内的权重服从高斯分布的特征来去除噪声点，并且保持原有的数据面貌，最终生成三维点云，用qij表示。其中高斯滤波函数表达式如式(1)所示。

(1)

其中，ωd代表的是权重；ωx,y为点云的邻域[9]。

2 重构镜片与优化

通过采样和去噪得到的点云数据只是曲面上的型值点，而要用NURBS表达出曲面，需要控制点、节点矢量和U、V方向的次数和权因子。因此重构镜片，需要反算出控制点和参数化点云数据来得到节点矢量。

2.1 NURBS曲面定义与一般性质

由于NURBS具有各种优越性，为曲面提供了统一的数学描述，并且在曲面造型中得到广泛的应用[10]。其中NURBS曲面齐次坐标表达式为

(2)

式中，di,j为控制点矩阵，就是本文要反算的部分，它呈拓扑矩形结构，控制曲面的形状和参数域内点的对应关系；Ni,k(u)和Nj,l(v)分别代表为u、v方向的规范B样条基；k和l代表次数；ωi,j代表权因子，对于曲面接近控制矩阵起到推拉做用。权值增加，曲面被推近控制点，权值减小，则远离。u、v参数属于节点向量U和V，它们的表示方法分别为U=[u0,u1,…,um+k+1]，V=[v0,v1,…,vn+l+1]。在大多数实际应用中，节点向量两端节点都取值为0和1，定义域范围表现为正方形，0≤u，v≤1，定义域被其内节点划线分成(m-k+1)×(n-l+1) 个子矩阵。NURBS曲面在定义域上被分割成子曲面，每个子曲面定义在单位正方域中某个具有非零面积的子矩阵域上[11]。

在按德布尔-考克斯递推公式决定的k次规范B条基函数，其递推式如式(3)所示。

(3)

在本文中，根据上述曲面表达式，由于三次样条在节点处可以达到二阶连续，因此本文在重构时，u、v方向的次数都选择3次。同时，由于权因子主要用于更加精确表示解析曲面(如圆柱面)，以及对于面型的修改，且选值有不确定性，在重构曲面过程中没有明显的几何意义。因此在反算过程中，选择将权值设置为1以简化本文反算的计算难度。

2.2 节点矢量参数化

考虑到曲面的表达式，欲构造一个曲面，正算方法除了要控制点和次数还需要确定节点矢量。控制矩阵所构造的控制网格只能控制曲面大体走向，而要曲面贴合型值点，需要选择较优的节点矢量参数化方法。本文选择修正弦长参数化法[12]，修正弦长参数化的表达式如下

(4)

其中，ki是修正系数，它对应的计算式为

(5)

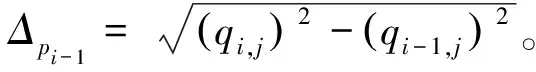
2.3 反算曲面控制点

为了让一条三次NURBS曲线通过一组型值点qi(i=0,1,…,r)，反算过程中由m+1个控制点构成的曲线的首末端点与qi相同，但要定义域内的(r+k+2) 个节点与曲线分段的连接点相对应，得到m=r+2。对于已知型值点qij，已知曲面次数为3，从曲线的推算可以得到曲面的控制点矩阵dij(i=0,1,…,r+2;j=0,1,…,s+2)。

因为前面设置权值ω=1，所以当本文将NURBS曲面的齐次坐标，投影到ω=1的超平面中心投影，所得到的三维表达式与四维齐次坐标空间的表达式一样[14]，因此本文将其次坐标表达式转换成式(6)。

(6)

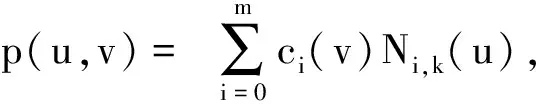
型值点的两端端点与控制点的端点的值相同，因此在计算控制曲线时，所求控制曲线个数比原先的个数少2，表达式转换成如下矩阵式(7)。

(7)

矩阵中的系数均为样条基函数的值，由节点向量中的节点值计算得到，为了方便计算，采用更直接的矩阵形式，有

(8)

其中，Δi=ui+1-ui，带入ai、bi、ci、ei组成由节点矢量计算出的系数矩阵，其中ai、bi、ci、ei的计算方法如式(9)所示。

(9)

整体曲面重构的算法流程如下：

步骤1通过给定的点云数据qij，为拓补阵列数据点的(m+1)×(n+1)形式；

步骤2固定参数v，通过上面一维的曲线反算方法，通过修正弦长参数法，以u为参数，因为参数v固定等同于V方向的j固定。因此带入计算的时候，qij变为了qi。由上述矩阵式，带入现有的型值点和节点矢量，通过矩阵计算式反求出每个控制曲线被截面曲面所相交的n+1个点Ci，这些点为截面曲线的控制顶点。沿着V方向遍历，能得到(m+1)×(n+1)个点；

步骤3对于截面曲线上的控制顶点Ci，沿着参数V的方向，依次取型值点C0,i,C1,i，…，Cm+1,i。对i取定值，按照修正弦长参数法对V向型值点进行参数化，继续利用上述曲线反算的方法继续进行插值；

步骤4经过两次线性矩阵进行反算，从而得到目标的控制点，将计算由二维的计算变成两个一维的计算，达到降低次数的目的；

步骤5再将控制点和u、v参数和权值带入三次NURBS曲面表达式中，从而重构出曲面。通过移动控制点或者增加、删减节点的办法，局部修改面型，从而得到理想渐进镜片，优化渐进片散光区太大等问题。

2.4 界定曲面局部修改

为了在修改镜片过程中保持镜片的球镜度不变，需要对镜片界定曲面进行修改。对于重构出来的曲面，有两类修改办法：(1)局限于一个参数方向，修改曲面的一条带部分；(2)局限于两个参数方向，修改对应于子矩阵矩形域的曲面部分。

因为渐进多焦点镜片是自上而下渐变，所以只需沿着一个参数方向修改一条带部分。沿着U方向，在镜片上的远视焦点和近视焦点中间选取合适两点u1和u2，这一点的u参数给定了一个被细化的u参数区间。因为曲面的次数是3次，有3个内节点被包含在细化后的区间(u1,u2)。在此区间内，因为空间被细化，可以找到一个新增控制点。该控制点更加靠近曲面，通过移动控制点和修改权因子，可以修改曲面的一条带部分，从而对界定曲面进行局部修改[15]。

3 算法实现与验证

本文采用MATLAB编程来实现镜片曲面重构的过程，并通过上述方法来进行验证。图2为镜片模型上采样得到的6 561个散乱点云图片。首先，对点云数据进行预处理和利用高斯滤波原理进行数据去噪，得到图3。为了重构曲面，通过扫描点云矩阵，利用修正弦长参数化得到节点矢量，带入型值点用矩阵计算求出各个控制曲线，其中由固定参数v反算得到其中一条控制曲线，如图4所示。得到控制曲线后，再利用参数u反算出各个控制曲线上的控制点，带入NURBS算法中，重构出镜片曲面，如图5所示。

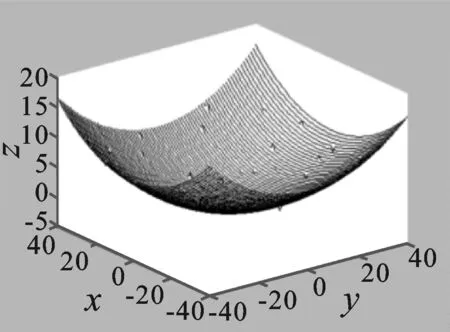
图2 原始图Figure 2. Original image

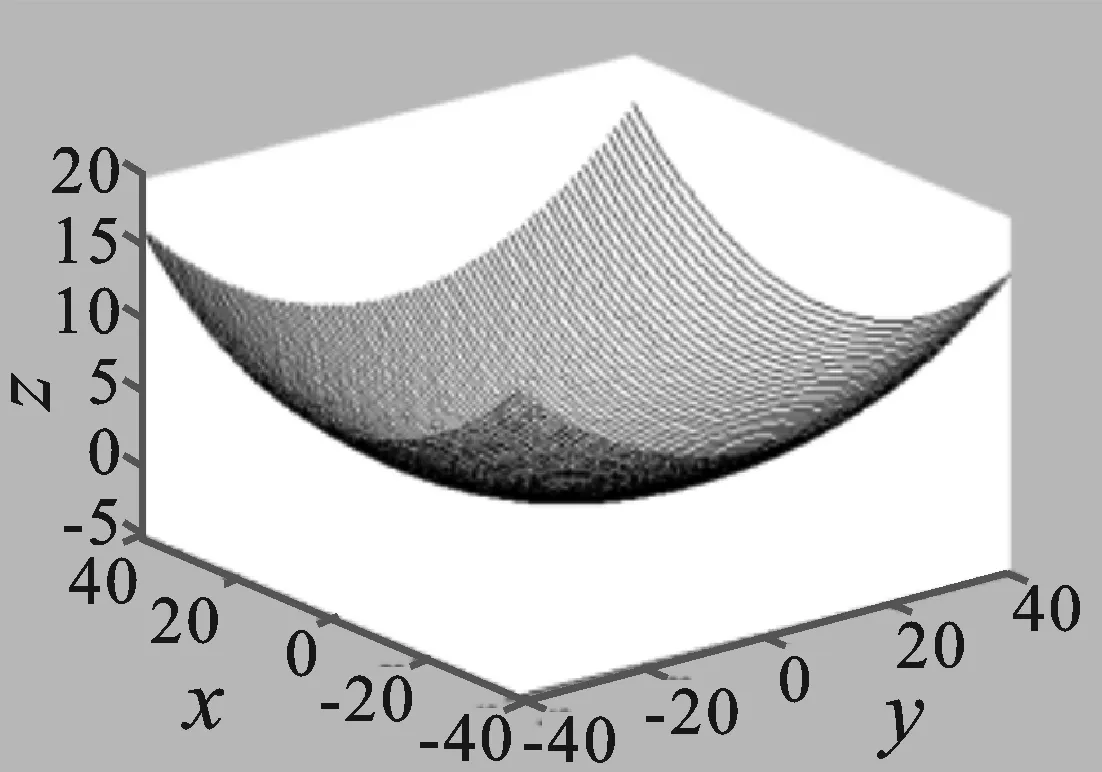
图3 去噪图片Figure 3. De-noisingprocessing image

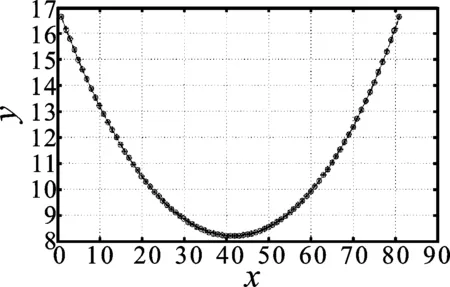
图4 控制曲线Figure 4. Control curve

图5 重构曲面Figure 5. Reconstructed surface

结合实验结果，为了比较重构出的镜片效果是否符合标准，利用上述生成的自由曲面，将生成的每个点以(x,y,z)的形式输出，保存为文本文件。通过公式计算出矢高，按照标准写成sdf文件。

为了解基于自由曲面技术的渐进镜片上屈光度的表面分布情况，选择利用基于莫尔偏折法原理的FFV仿真软件对渐进镜片进行测量比较[16]。根据处方单LMS中，设置中心厚度、基弯、加工直径等参数，加载sdf文件，可以模拟出所设计镜片的球镜度分布图、柱镜度分布图、畸变分布图和横截面屈光度变化曲线图。图6为工号为MD9_100镜片仿真结果。

由图6(a)可以看出，重构镜片中的ADD在处方单中设置的是1.0 D，仿真结果相差0.03 D，且图片中球镜度分布均匀，从远视区到近视区过度平缓均匀，符合渐进片设计要求。对比图6(b)和图6(c)中可以发现，柱镜和畸变值接近，可以近似看作镜片的像差，而柱镜度只有0.02 D。说明镜片的像差小，在矫正过程中不会引入过大的像差[17]。图6(d)代表镜片中截面屈光度的变化情况，曲线从上到下分别为a、b和c。a曲线代表球镜度变化，b曲线代表柱镜度变化，c曲线代表畸变的分布情况。其中，球镜度变化曲线从远视区基准点的度数开始到近视区，无明显跳变，度数变化过程平滑且缓慢。柱镜度变化曲线与畸变曲线重合，且在通道变化处的数值都很小，符合渐进片设计要求，证明了NURBS重构的有效性。

为判断通过界定局部修改的镜片是否达到了本文的研究目的，将生成的曲面重复上述过程，生成sdf文件并进行FFV仿真。将仿真生成的球镜度分布图和柱镜度分布图与图6进行比较，可以看出局部修改后镜片的球镜度没有变，达到了实验目的。如图7所示为修改后的镜片仿真图。

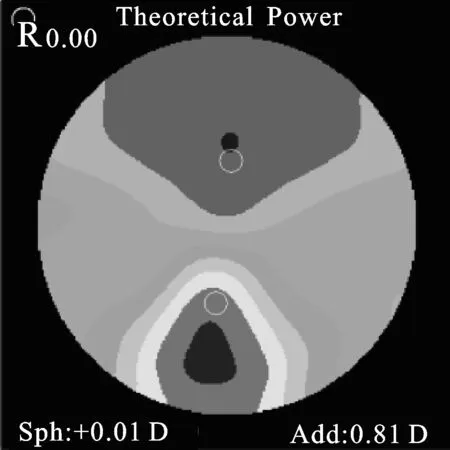
为了判断生成的曲面是否光顺，需要对重构出的曲面进行光顺性分析。文献[18]概括的曲面光顺准则中提到，需要高斯曲率变化比较均匀。图8为利用MATLAB软件算出的曲面高斯曲率变化图，图中曲率变化均匀，无突兀变化，在远视区和近视区的分界明显，证明重构出的镜片光顺性较好。

图8 镜片高斯曲率分布图Figure 8. Distribution of the gaussian curvature radius of lens

4 结束语

本文通过用渐进片上的型值点重构出NURBS曲面，通过修改控制点和权因子来改变面型的方法，对渐进片设计过程中的修改问题进行研究。在型值点重构的过程中，需要通过对点云数据进行去噪才可以使用。重构过程中的参数化方法不同导致最后的结果也有差别。通过NURBS重构出的镜片，其球镜度的远视区、渐进区和近视区的连接处过度更加平缓，连接处的曲率变化稳定，设计出的镜片光顺，且通过对曲面进行局部修改能够保持球镜度不变，证明了本文算法的有效性。