基于自适应牵制控制的中立型复杂网络渐近同步

时 慧，童东兵

(上海工程技术大学 机械与汽车工程学院,上海 201620)

分布式供电技术在实现节能减排、提高能源利用率方面有着重要的作用。分布式能源互联网中包含众多供能设备，每个供能设备状态的变化对其经济运行状态会产生直接或者间接的影响。在能源互联网运行过程中，供能设备之间通过通信进行经济调度，而设备之间的通信状态可以用复杂网络来描述[1]。近年来，复杂网络的稳定与同步问题得到了学者们的关注[2-3]。由于中立项的存在，使得中立型复杂网络同步控制准则的求解比一般复杂网络更加困难。这意味着复杂网络的理论成果不能直接推广到中立型复杂网络中。因此，本文对中立型复杂网络的同步研究具有实际意义。

控制策略能够使生物神经网络具有更好的输出性能，并对外部信息的激励做出一致响应[4]。由于信号在传输过程中可能会受到外界环境的干扰，从而导致信号微弱或中断，因此不连续控制更适用于实际系统中。不连续的状态反馈控制包括间歇控制[5-7]、开关控制[8]、牵制控制[9-11]和采样-数据控制[12-14]等。近年来，牵制控制因其高效且经济[15-16]的特点，逐渐成为了人们研究的重点。由于牵制控制方法仅需要控制网络中的一小部分节点，因此牵制控制能够有效降低控制成本[17]。

本文研究了具有时滞和耦合节点的中立型复杂网络的渐近同步问题，提出自适应牵制控制策略，并设计了自适应更新律，保证中立型复杂网络能够达到渐近同步。通过构造适当的Lyapunov函数，利用LMIs(Linear Matrix Inequalities，LMIs)获得了渐近同步判据。最后通过数值仿真，计算出中立型复杂网络达到渐近同步所需最少控制节点数，并进一步验证了渐进同步判据的有效性及实用性。

1 问题描述

在分布式微网中，各个微源与相邻的微源可能会相互影响，这可以被看作微源节点间的耦合。分布式微网中各个微源节点可以被看作有向图的顶点，考虑一个有n-维度状态变量向量yj(t)=[y1j(t),y2j(t),…,ynj(t)]T的中立型复杂网络如下

(1)

分布式能源互联网通信过程中存在着一系列的延迟，这会使得通信网络不稳定。因此考虑时滞对中立型复杂网络(1)的影响是必要的。另外，为了通信网络能够克服时滞等因素对节点的影响并达到稳定，将自适应牵制控制器引入yj(t)的中立型复杂网络(1)中。因此，考虑一类带有时滞和自适应牵制控制器的中立型复杂网络，可以被描述为如下

(2)

(3)

为了减少控制消耗和同步损失，系统(2)中的自适应牵制控制器被设计为

(4)

(5)

结合式(2)～式(5)，令

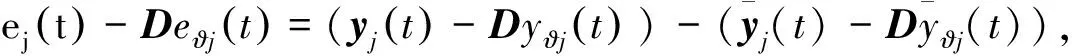
(6)

为了进一步证明中立型复杂网络误差系统(6)是渐近稳定的，给出了以下假设和引理：

‖f(z1)-f(z2)‖≤κ‖z1-z2‖

(7)

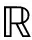
假设2中立型复杂网络误差系统(6)中的激活函数f(·)满足特性

yTf(yϑ)≤εyTy，∀y∈Rn

其中，ε∈(0,∞)是已知的常数。

假设3假设中立型复杂网络误差系统(6)的耦合函数

满足ψ(yj(t),yj(t))是连续映射且满足Lipschitz条件；在正常数α> 0，则满足

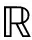
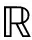
MTN+NTM≤δMTM+δ-1NTN， 其中ε>0。

引理3对两个n×n的Hermitian矩阵X和Y，矩阵X、Y和X+Y的特征值分别为ρn≤…≤ρi≤…≤ρ1，pn≤…≤pi≤…≤p1，qn≤…≤qi≤…≤q1，则有ρi+p1≥qi≥ρi+pn,i=1,2,…,n成立。

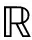
其中，λmin(M-1N)和λmax(M-1N)分别是M-1N的最小特征值和最大特征值。

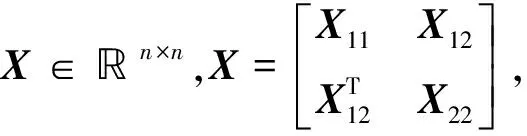
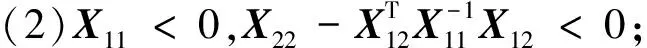
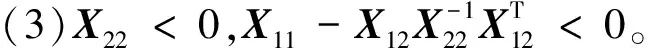
2 主要结论

定理1当假设1～假设3成立，对中立型复杂网络误差系统(6)中的节点施加牵制控制，如果存在一个矩阵G> 0和ξ个节点使得如下不等式成立

(8)

Ω2=δκ-(1-ϑ)γ≤0

(9)

式中，Pξ表示除去原矩阵P的前ξ行和前ξ列得到的子矩阵；[(BT+B)/2]ξ表示除去原矩阵(BT+B)/2的前ξ行和前ξ列得到的子矩阵；ρ=‖(BT+B)/2‖2，γ=‖(GT+G)/2‖2，δ=‖(DT+D)/2‖2。则中立型复杂网络(3)能够与平衡系统(2)是渐近同步的。

证明考虑一个合适的Lyapunov泛函如下

(10)

其中，θ是一个待定常量。

通过Itö公式，中立型复杂网络误差系统(6)和式(10)，可以得到

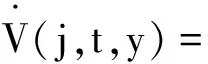
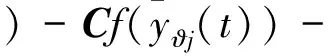
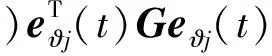
(11)

根据假设1～假设3，并结合引理1和引理2，可以得到

(12)

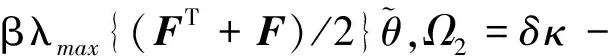
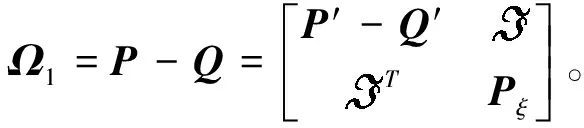
结合引理3，可得

(13)

λmax(Pξ)≤0

(14)

再结合式(14)和引理4，有

(15)

根据式(15)和引理5，得式(16)。

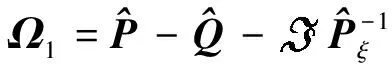
(16)

3 仿真实例

本节将通过一个数值仿真来验证所获得理论结果的正确性和有效性。

考虑一个具有5个节点的中立型复杂网络误差系统(6)具有如下系统参数

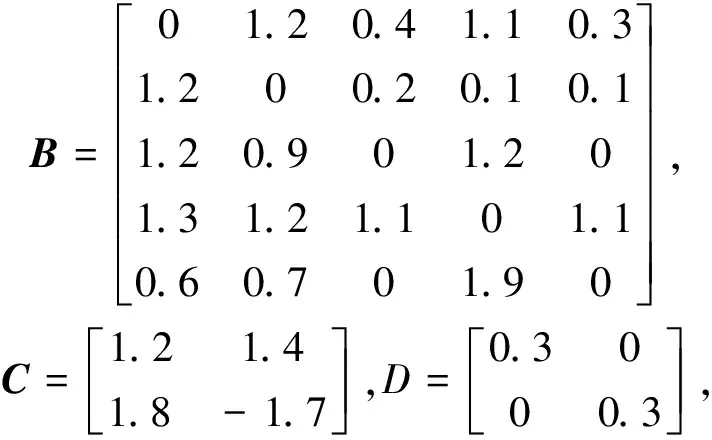
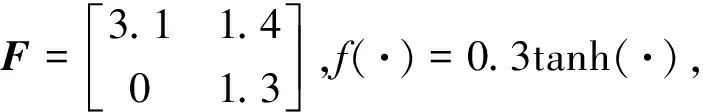
α=0.3，λ=0.47，ϑ=0.12，β=1.82，qi=0.2，E=2.6。

将中立型复杂网络误差系统(6)的初始值设置为

ej(t)=[e1j(t),e2j(t)]∈[-1,2]，j=1,2,…,5，t∈[0,2]。

经过验证，假设1～假设3得到满足。通过LMI工具箱，求解定理1中的式(8)和式(9)，并得到如下结果

λmax{(BT+B)/2}1=1.770 4>1.362 8，

λmax{(BT+B)/2}2=1.630 8>1.362 8，

λmax{(BT+B)/2}3=0.995 0≤1.362 8。

注释1拓扑矩阵的子矩阵的最大特征值会随着子矩阵的维度减小而减小，于是可以得到λmax{(BT+B)/2}4<1.362 8，λmax{(BT+B)/2}5<1.362 8。

因此，当ξ=1, 2时，定理1中的LMIs式(8)和式(9)无解；当ξ=3, 4, 5时，LMIs式(8)和式(9)有解，本文所研究的渐近同步准则是正确有效的。实验结果表明，有效地选择控制参数及节点可以使该算法较好地收敛到最优值。

由于控制器所需节点越少成本花费越低，因此自适应牵制控制器(4)选择对3个节点进行控制，3个控制增益的动态曲线如图1所示。在自适应牵制控制器的作用下，使中立型复杂网络(3)能够与平衡系统(2)达到渐近同步。带有自适应牵制控制器(4)的中立型复杂网络误差系统ej(t)的动态曲线如图2所示。由图2可看出，基于自适应牵制控制策略的中立型复杂网络能够逐渐收敛为零，证明了自适应牵制控制策略的有效性。目前，大多数牵制控制器不能得知控制节点的数目。本文通过掌握控制节点数目可以减少控制成本，具有重要的现实研究意义。

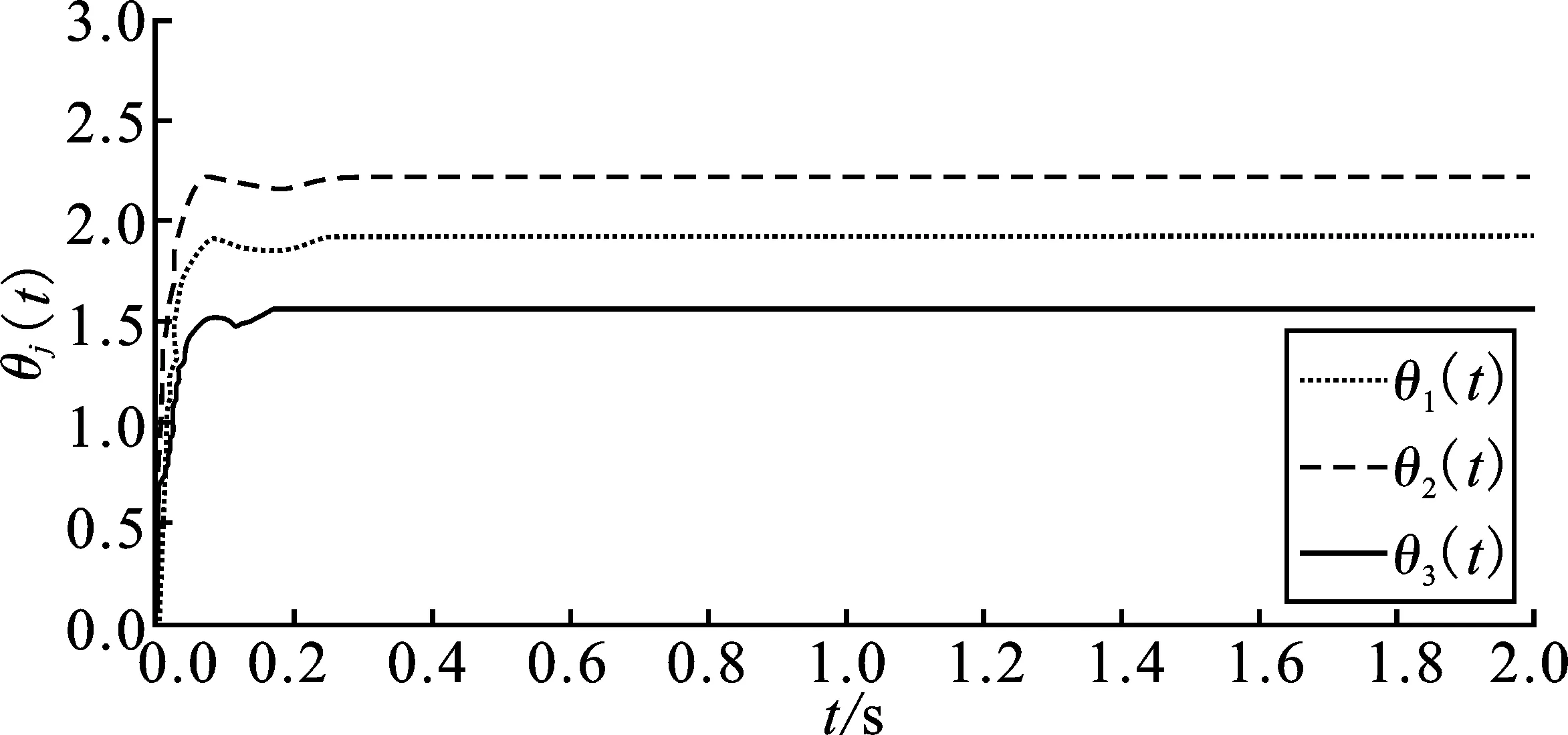
图1 自适应控制增益θj(t)，j=1,2,3的状态轨迹Figure 1. State trajectories of Adaptive controlgainθj(t),j=1,2,3

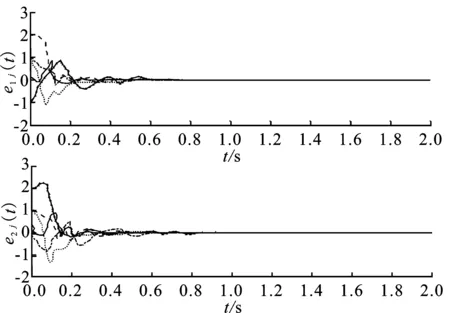
图2 中立型复杂网络ej(t)，j=1,2,…,5的状态轨迹Figure 2. State trajectories of neutral coupled neural network system ej(t),j=1,2,…,5

注释2在文献[18]中，控制器需要得到所有节点的信息，而本文中能确定牵制节点的个数，因此只需要获取部分节点的信息。文献[18]中虽然考虑了两个节点之间存在耦合，但是其耦合矩阵只与一个节点的状态相乘，而本文的耦合矩阵与耦合的两个节点相乘。此外，本文系统状态达到稳定的时间比文献[18]中更早。

4 结束语

本文针对具有时滞和耦合节点的中立型复杂网络渐近同步问题，设计了一个自适应迁至控制策略，并给出了一些中立型复杂网络的渐近同步判据。本研究通过最后的数值仿真，验证了所给的渐近同步判据，并计算出同步所需最少控制节点数，解决了大部分网络中牵制控制器的节点数未知且测量成本较高的问题。未来研究的目标是将中立型系统与实际应用相结合，添加更多不确定项，弱化本研究中的给定条件，导出具有更低保守性的同步判据。