高架车站自振特性分析与对比

罗 伟，陈 帅，汪子豪，刘 晓，李哲旭，严 鹏

(1. 长江勘测规划设计研究院, 湖北 武汉 430072；2. 武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072；3. 武汉大学水工岩石力学教育部重点实验室，湖北 武汉 430072)

随着我国基础建设的发展，地铁、桥梁、车站等结构建筑不断兴建。表征复杂结构的重要参数—自振频率也愈加重要。自振频率的合理计算关系到结构受到外部荷载作用下振动响应的准确评价，是判断结构是否发生共振的重要依据。因此，在满足精度要求下，如何快速且准确地求取结构自振频率，把握其自振特性尤为重要。

目前求取自振频率的方法[1-6]有很多，本文主要依托武汉高架车站施岗站开展研究，采用平面模型理论分析、数值模拟和尾波法三种方法进行对比分析。

施岗站[7]位于武汉地铁21号线，车站呈东西走向，平行于汉施公路布设。车站总长141.6 m，宽度24.4 m。车站为路中高架三层侧式车站，采用桥建合一的结构体系，桥墩采用双柱。站台屋盖采用轻型钢结构。纵向为10轴8跨，在4、5轴间设一道变形缝，缝宽100 mm。车站首层为车站架空层，二层为车站站厅和设备层，三层为车站站台层，车站如图1所示。

1 平面模型理论分析

多自由度体系的自由振动求解方法[8]有两种：刚度法和柔度法。刚度法通过力的平衡方程求解，柔度法通过建立位移协调方程求解。对于多层刚架等结构，常常采用刚度法更为便利。

如图2所示为一个简化的两自由度体系的剪切型框架结构[8]，两自由度体系的自由振动有

图2 两自由度体系的动力平衡

(1)

推广到n个自由度，则有

(2)

与其相对应的振幅方程为

(3)

(4)

令i=1，2，…，n，可得与n个ωi相对应的n个主振型向量{A(1)}，{A(2)}，…，{A(n)}。

1.1 计算模型

基于前述计算原理，建立施岗站二维平面模型(图3中实线平面模型)，对结构的纵向、横向自振特性进行结构力学计算。其中，对于车站模型简化，将复杂结构按承重特性划分，分为承重结构与非承重结构。承重结构为建筑物整体提供有效质量与刚度，对自振频率有重要影响。非承重结构对自振频率影响很小，作简化处理。

1.2 结果分析

基于上述原理，对施岗站的纵向、横向自振特性进行结构力学计算，获取其自振特性。其中1阶振型见图3虚线所示，各阶自振频率结果见表1。

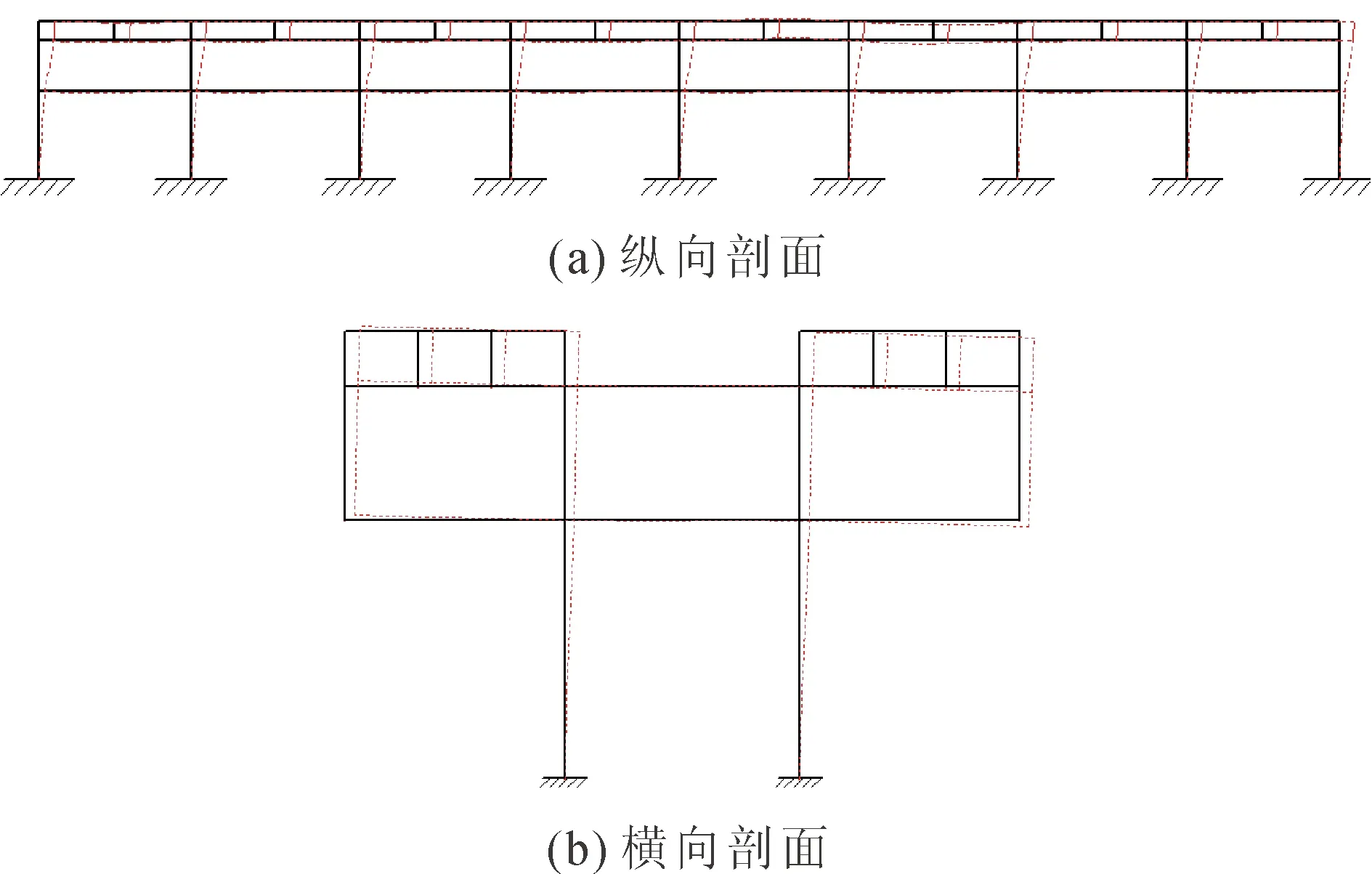
图3 施岗站二维平面计算模型与1阶自振振型

表1 基于理论分析的施岗站自振频率(前10阶) Hz

由图3和表1可知，车站纵向剖面的前10阶自振频率约为3.0～11.0 Hz，其中1阶频率3.36 Hz。车站1阶振型为沿车站纵向的偏移，而其它振型主要体现车站竖直方向变形或翘曲。车站横向剖面的前10阶自振频率约为5.0～59.0 Hz，其中1阶频率4.96 Hz。车站1阶振型为沿车站横向的偏移，而2、3阶振型主要为车站竖直方向变形。

考虑到平面模型对三维复杂结构的简化，二维平面模型无法准确反映车站的复杂特性，但平面模型理论分析可以在一定程度上反映复杂结构在单个剖面上的自振特性。

2 数值模拟模态分析

2.1 计算模型

依据施岗站设计资料，建立车站主体混凝土结构三维有限元模型，网格数量约44万，在进一步细化结构各材料差异后，对应赋入属性，如图4所示。

图4 施岗站三维数值模型

2.2 结果分析

通过模态分析，得到车站前10阶自振频率，如表2所示，图5以1阶振型为例，给出振型形态。

表2 基于数值模拟的施岗站自振频率(前10阶) Hz

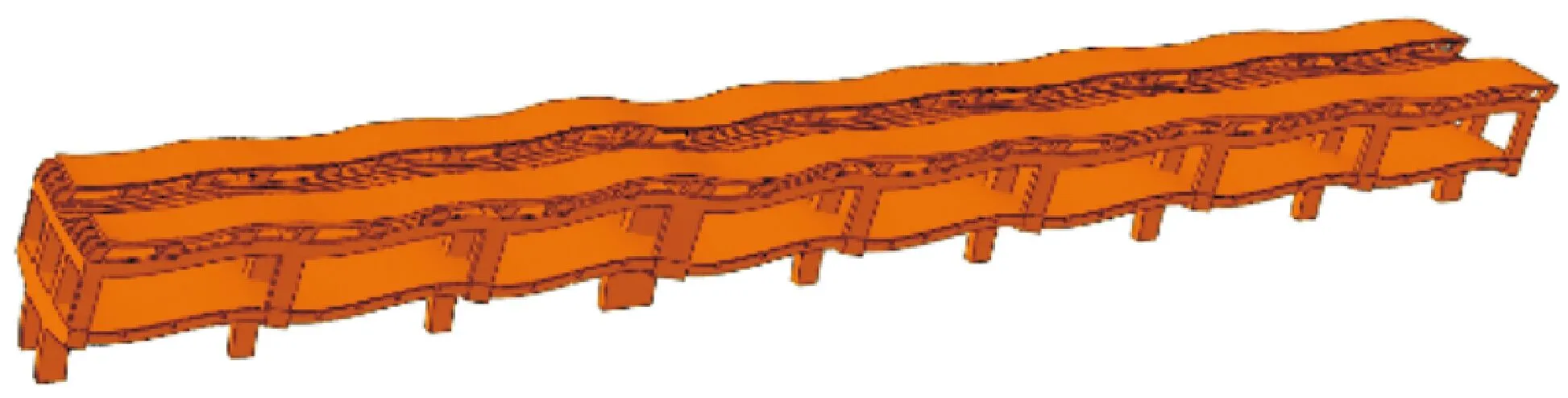
图5 施岗站三维模型1阶振型

由表2和图5可知，低阶模态中1阶频率约为3.97 Hz，振型主要反映车站整体的纵向偏移；而2、3阶频率约为4.0～4.3 Hz，振型均为主体结构的扭转，以车站结构中心为界，两侧向不同方向扭转；高阶振型(>5 Hz)主要体现竖直向变形、翘曲。

3 尾波法自振分析

根据相关理论基础，结构自振频率的确定可以通过研究结构的自由振动响应来实现，结构的阻尼自振主频pd可由阻尼比β和无阻尼自振主频p由下式计算得到：

(5)

一般结构的阻尼比β为5%，因此结构阻尼振动主频在一定程度上可以近似认为与结构的无阻尼振动主频相等，即：pd=p。

结构在外部振动波的作用下将产生强迫振动，当荷载振动波作用结束之后，结构将进行自由运动，此时结构将以阻尼振动主频的频率来振动[9]。结构自由振动波形即为结构振动响应尾波，当阻尼比较小时，阻尼振动周期Ts可近似等于自振周期T。

因此，结合施岗站现场监测试验，开展实测尾波分析。

3.1 现场试验

本次现场测试试验，选用Blast-Cloud Monitor振动测试仪，选取测点位于列车轨道层(1号、2号、3号)、站台层(4号、5号)、站厅层(6号、7号、8号)和墩柱(9号)，具体测点位置如图6所示。

图6 车站监测测点布置示意图

3.2 测试结果及分析

根据列车以10～40 km/h匀速行驶和进出站时的车站不同位置的振动尾波数据(共33组)，对数据进行频谱分析，获取主频，绘制如图7所示。同时，根据图中频率集中程度与分布范围，拟定典型频率集中区间作为第一、第二频率区间来进行分析，列于表3。

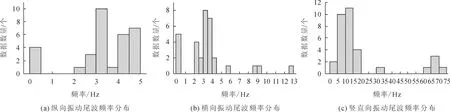
图7 车站振动尾波主频分布

由表3可知，对于车站纵向，频率主要集中在3.0～5.0 Hz，其中，又以两个区间为主，第一主频区间，约为3.0～3.5 Hz, 第二主频区间约为4.0～5.0 Hz。车站横向主频集中于2～4 Hz，竖直方向则以5～15 Hz，60～75 Hz为主。

表3 基于尾波测量的施岗站自振频率分布区间 Hz

4 结 语

依托施岗站高架车站，通过理论分析、数值模拟和尾波法三种方法对高架车站自振特性进行分析与探究，初步结论如下：

1)采用上述三种分析方法得到的车站自振频率结果在主频区间上基本保持一致：低阶主频约3.0～5.0 Hz，主要表现为纵向平动或扭转；高阶主频处于5.0 Hz至几十赫兹，表现为竖直向变形或翘曲等。

2)平面模型理论分析和数值模拟方法能够获取高架车站的多阶自振频率和振型，适用性强，但对高架车站结构存在不同程度简化；尾波法以实测数据为依据，能够获取有限阶次自振频率的分布范围，考虑了高架车站实际复杂特性，准确度高，但实际工作量大。上述三种方法的综合应用能够保证高架车站自振特性评估更为合理、准确。