mKd V方程新的有限维可积系统

徐 英，王建文

寻找新的有限维可积系统是孤立子理论研究中的重要课题之一.1989年，曹策问教授提出了一个构造有限维可积系统的非常有效的方法—谱问题非线性化方法［1-4］，该方法已被系统研究和发展［5-17］，很多的孤立子方程的有限维可积Hamilton系统已通过该谱问题非线性化方法得到.具有物理意义的孤立子方程常常可以从一般的孤立子方程中约化得到.约化条件使这类方程的研究十分困难，2007年，周汝光教授在文献［18-19］中给出了解决此类问题的一个方法，通过选取适当的谱参数和耦合上谱的复共轭谱问题，得以实现约化系统的谱问题非线性化.应用此方法，谱参数为互异非实复数下的非线性Schro¨dinger方程、mKdV方程、导数非线性Schro¨dinger方程、WKIS方程以及矩阵导数非线性Schro¨dinger方程的有限维可积Hamilton系统被找到［18-21］.文献［22］中的方法在沿用了文献［18-19］中方法基本思想的同时做了一定改进，采用了双非线性化方法，获得了任意互异谱参数下非线性Schro¨dinger方程的有限维可积Hamilton系统.随着进一步研究，文献［23］提出了使用范围更广更简便的方法，其基本思想是选取合适的谱参数和特征函数将原谱问题扩大，从而约化系统的谱问题非线性化通过上述已扩大的谱问题得以实现，该方法不仅获得了任意互异谱参数下KdV方程的有限维可积Hamilton系统，同时揭示了mKdV方程族和AKNS方程族之间的关系.本文将应用文献［23］中的方法，研究mKdV方程的谱问题线性化，以获得任意互异谱参数下mKdV方程新的有限维可积系统.

1 AKNS方程及其约化

考虑如下AKNS谱问题

其中：λ是谱参数，u，v是位势函数.

选取式（1）的辅助谱问题

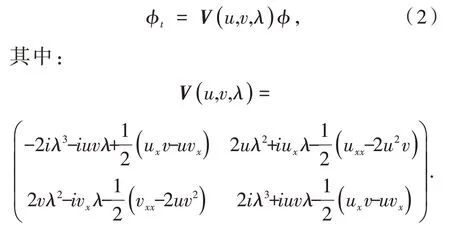
由式（1）与式（2）的相容条件，即零曲率方程

可得AKNS方程为：

式（3）在约化条件v=-u下，可化为mKdV方程如式（4）.

2 AKNS方程的谱问题非线性化

选取m个互不相同的谱参数λ1,λ2,…,λm，考虑相应的AKNS谱问题

其 中：Φ1=(φ11,…,φ1m)，Φ2=(φ21,…,φ2m)，A=diag(λ1,λ2,…,λm).

F1,F2,…,Fm是式（10）和式（11）的守恒积分，同时可以验证L()λ满足r矩阵关系，从而守恒积分对合，即{ }Fj,Fl=0，j,l≥1.又因为选取的λ1,λ2,…,λm互 不 相 同，所 以 守 恒 积 分F1,F2,…,Fm是函数独立的.综上所述，可得下述命题.

命题1有限维Hamilton系统（10）（11）在Liouville意义下是完全可积的.

3 mKd V方程的谱问题非线性化

通过简单的验证，可得如下结论.

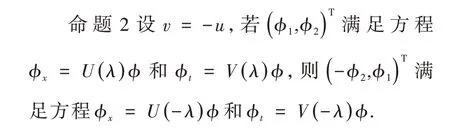
为了进行mKdV方程的谱问题非线性化，只要对AKNS方程的谱问题非线性化进行修改即可.选取N个互不相同的谱参数λ1，λ2,…,λN，因 此λ1,λ2,…,λN,-λ1,-λ2,…,-λN互不相同.

考虑如下相应的mKdV谱问题

在约束（17）下，类似于空间部分，可得时间部分的如下有限维Hamilton系统：

又因为由式（12）定义的守恒积分F1，F2，…，F2N是对合并且独立的，所以可得以下定理.

定理1有限维Hamilton系统（18）（19）在Liouville意义下是完全可积的.

4 结语

文章给出了mKdV方程的谱问题非线性化，从而得到了任意互异谱参数下mKdV方程新的有限维可积系统.众所周知，mKdV方程可由著名的AKNS方程约化得到.为了实现mKdV方程的谱问题非线性化，首先回顾了AKNS方程的谱问题非线性化，然后选取合适的谱参数和特征函数将原mKdV方程的谱问题扩大，找到一组新的变量使得扩大化了的谱问题可写成AKNS谱问题形式，从而直接运用AKNS方程的谱问题非线性化过程得到了任意互异谱参数下mKdV方程新的有限维可积系统.需要指出的是，这个合适的特征函数的寻找并非易事.另外，同样的方法可以推广应用于其他带有约化条件的孤立子方程，值得进一步继续研究.