基于倒谱分析的防混响时延估计算法
赵中华,李竞荣,邓德迎
(桂林电子科技大学 信息与通信学院, 广西 桂林 541004)
0 引言
声源定位技术因设备隐秘性好、不易被察觉、不受光线强度的影响、感知角度全面,广泛应用于军事领域和民用领域。长期以来,传声器阵列一直是语音信号处理中使用最广泛的信号获取技术,用传声器阵列实现定位的方法主要有基于最大输出功率的可控波束形成技术、基于高分辨率的谱估计技术、基于到达时间差(time difference of arrival, TDOA)的定位算法。基于TDOA的定位算法复杂度小,硬件成本低,容易实现,在单声源定位中具有非常好的性能,应用最广泛。该方法主要分为两个阶段:延时估计和定位算法,如果延时的取值不准确,在定位阶段产生累计的误差会影响定位结果。
最经典的时延估计算法是广义互相关(generalized cross correlation, GCC) 算法[1],该方法在信号和噪声不相关、信噪比高的条件下估计性能很好,然而室内声源定位的干扰信号主要来自混响声,和声源信号具有相关性,所以传统的时延估计技术如果直接用于室内声源定位,估计性能会严重下降。
为了解决混响干扰问题,2000年BENESTY[2]提出了基于自适应特征值分解的时延估计算法,利用接收信号的协方差矩阵估算出房间脉冲响应,求出直达声对应的信息,得到声音传播的时间延时,该方法可以克服混响声的干扰,但矩阵运算会有很大的运算量;后来 DOCL等[3]对自适应特征值分解的算法做了改进,通过对接收信号做白化处理降低算法对信噪比的要求,提高了算法的抗噪性;2010年 MOSAYYEBPOUR等[4]用自适应滤波的方式估计出传声器对应房间脉冲响应的逆,降低了混响对声源信号的干扰;后来他使用同态滤波法滤除混响[5],这种算法适用于多种语音信号,但减弱了信号之间的相关性,容易使相关函数的峰值变模糊;2015年EHSAN等[6]提出一种基于线性卷积混合模型的去噪技术,虽然能将声源信号从接收信号中分离出来,但算法较复杂;2019年,徐海涛[7]提出一种基于Gammatone分频滤波和Wigner-Ville分布的时延估计法,可以减弱混响对估计结果的干扰;同年,李悟等[8]通过探测室内反射物体实现了室内空间结构的重建,得到更精确的混响模型,有利于混响声和直达声的分离,但该方法需要用定向声源估计混响模型,无法直接用于被动式的声源定位系统;2020年,马凯等[9]提出基于分数阶傅里叶变换的自适应最小均方误差(least mean square, LMS)滤波算法,在混响环境中能提高接收信号的有效性,虽然通过自适应步长LMS算法提高了收敛速度,但运算量依然很大;同年WANG等[10]利用深度学习算法从接收信号中预测直达声分量,但这种方法需要大量的数据计算房间脉冲响应,不适用于实时性要求较高的声源定位系统。
笔者主要对室内声源定位中的延时估计算法进行分析,在封闭环境,通过分析信号在倒谱域上的分布滤除混响声部分,对单声源情况下的延时估计技术提出改进方案,这种方法保留了声源信号的更多信息,提高了延时估计的精度,估计结果更加可靠。
1 常用的延时估计技术
1.1 基本互相关时延估计法
因为声源信号是向四周辐射的,无法得到信号到达接收器的具体时间,因此需要通过比较两个接收器的接收信号在时域上的相似程度才可以估计出接收信号之间因为传输路径的不同而引起的时间延时。
假定室内声源为点声源,在远场模型下以平面波的方式进行传播。设两个传声器mi和mj接收到的信号,经过AD转换、滤波、加窗分帧等预处理操作后分别为xi(n)和xj(n),信号模型对应如下:
(1)
式中,s(n)表示声源发出的声音信号;hi(n)和hj(n)分别表示传声器位置的房间脉冲响应;wi(n)和wj(n)分别为声场中的加性噪声。
因为在预处理过程中,已经对接收的信号进行了加窗分帧处理,根据语音信号的短时平稳性,可以用处理平稳信号的方法处理每一帧信号。根据式(1),求出传声器mi和mj接收信号的互相关函数为
Rij(τ)=E[xi(n)xj(n-τ)],
(2)
根据式(2)可以求出互相关函数的值。
设中间变量为
(3)
则
Rij(τ)=E[si(n)sj(n-τ)]+E[si(n)wj(n-τ)]+
E[wi(n)sj(n-τ)]+E[wi(n)wj(n-τ)]。
(4)
假设室内的噪声只有不相关的高斯白噪声,在理想情况下,式(4)的后三项为0,所以有
Rij(τ)=E[si(n)sj(n-τ)]。
(5)
互相关函数峰值对应的时间延时则为估计的时间延时:
(6)
该方法对噪声特性的要求比较苛刻,在实际生活中难以得到广泛的应用。
1.2 GCC时延估计法
因为实际环境中除了高斯白噪声还有其他种类的噪声,所以按照基本互相关的方法估计时间延时,互相关函数容易出现伪峰,估计误差比较大。为了减小估计误差,就引入了GCC时延估计法,通过加权函数来增加信号的有用成分,以此来提高信噪比,抑制噪声的干扰,使估计性能提高。
分别对两个传声器预处理后的信号xi(n)和xj(n)做傅里叶变换,得到其在频域的信号Xi(k)和Xj(k),对Xj(k)取共轭得到Xj*(k),根据这些值进一步求出它们的互功率谱:
(7)
通过在互功率谱前选取不同的加权值φ(k),可以达到抑制噪声、锐化互相关函数Rij(τ)峰值的效果。常用的加权函数有ROTH处理、SCOT平滑相干变换、最大似然加权函数ML、相位变换PHAT等。
PHAT方法通过白化频谱的方式消除信号幅度的影响,只保留信号的相位信息,能兼顾到算法的复杂度和误差性能,估计效果最理想,因此使用最广泛。其加权函数为
(8)
加权后对得到的信号做反傅里叶变换,得到时域信号:
(9)
求出其峰值对应的时延:
(10)
即为估计时延。
综上,可以得到广义互相关法的处理流程如下:

图1 广义互相关算法流程Fig.1 Diagram of generalized cross-correlation algorithm
该方法在高信噪比、低混响的条件下可以获得比较理想的估计效果。但实际应用中,该条件很难满足,抗噪性能通常不能达到要求。
2 倒谱分析
广义互相关算法虽然有了非常多的改进方案,但比较适合处理加性噪声,在室内声源定位实现中,混响是主要的干扰信号[11],接收信号中存在大量的反射声使信号的功率谱图形脉冲变大,包含许多虚假的谱峰,要实现时延估计必须消除混响的影响,使谱图更接近真实的功率谱图。
笔者在已有的同态滤波基础上,根据声源信号的倒谱特性和房间脉冲响应在倒谱的分布情况,以提高时延精度为目的,提出一种适用于高混响环境的新时延估计方法。
2.1 同态滤波
因为混响和声源信号具有相关性,广义互相关时延估计算法没办法处理混响的影响,所以在混响比较严重的室内声场做时延估计,需要对接收信号做处理才能使估计误差降低,同态滤波是一种比较有效的降低混响干扰的方法。
房间脉冲响应作为一个非最小相位系统,可以分解为全通系统和最小相位系统,即
h(n)=hall(n)*hmin(n)。
(11)
声源信号通过以上系统时得到的声音信号可以分为全通部分和最小相位部分。因为相对时间延时τ在频域中可以用e-jwτ表示,对任意频率其幅值都是1,满足全通滤波器的条件,所以只会影响到全通系统的部分。
同态滤波是一种将接收信号中的最小相位分量和全通分量进行分离的技术,操作流程如下:

图2 同态滤波流程Fig.2 Diagram of cepstral filtering
在室内声场中,预处理后的接收信号x(n)在频域中的表达式为
X(k)=S(k)H(k)+N(k),
(12)
求接收信号的倒谱[5],有

(13)
式中,s′(n)、h′(n)、n′(n)分别表示声源信号、房间脉冲响应、加性噪声在倒谱域的表达式。
同态滤波[12]后得到最小相位部分的倒谱为
xmin′(n)=x′(n)[2u(n)-δ(n)]。
(14)
接收信号的最小相位部分对应的频谱为
Xmin(k)=exp{FFT[xmin′(n)]},
(15)
可以求出接收信号的全通分量为
(16)
将以上信号变换到时域中,代入到GCC延时估计的输入中,就可以得到滤除混响干扰后的时间延时。该方法因为是直接对接收信号做处理,会损失声源信号的部分信息,使得接收信号之间的相关性降低。
2.2 改进方案
考虑到时间延时主要体现在房间脉冲响应的全通部分,所以如果在倒谱滤波中能保留声源信号的所有部分和房间脉冲响应的全通部分,将会得到比较好的时延估计效果。
接收信号在倒谱域可以表示为
x′(n)=xmin′(n)+xall′(n)=smin′(n)+hmin′(n)+sall′(n)+hall′(n)。
(17)
以下讨论如何在保留hall′(n)和更多声源信号的条件下滤除hmin′(n)部分。
在接收信号最小相位部分的倒谱中,声源信号和房间脉冲响应的分布情况[13]为声源信号的声门和声道部分,以及房间脉冲响应的最小相位部分,分布在倒谱中的原点附近,而基音部分在倒谱的高时段区域,可以根据基音周期在倒谱上的位置将二者区分开来。
本文使用Long-pass lifter滤波的方法,滤除掉房间脉冲响应的最小相位部分。考虑到基音周期估计算法的复杂性会增加运算量,这里通过基音周期的范围确定倒谱域上基音频率对应的基音周期的范围,以其最小值为分界线实现滤波,然后对滤波后的信号做分析。
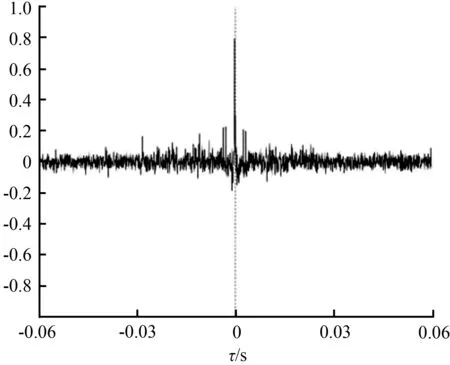
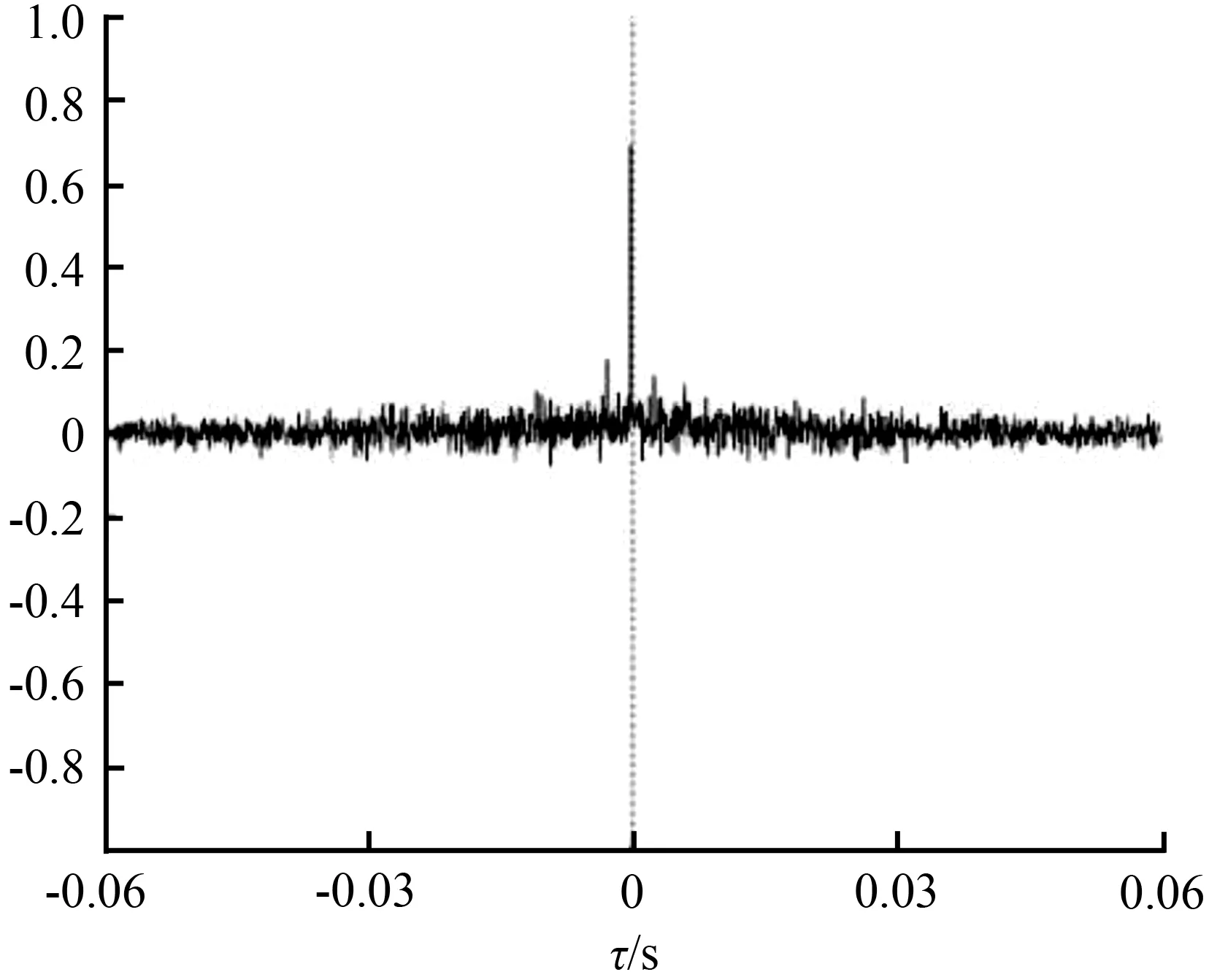
设基音频率fc的范围为fc-min fs/fc-max (18) 所以对接收信号的最小相位部分做滤波后,得到: (19) 式中,Nd必须大于基音周期tT′。 最后得到的接收信号为 (20) 改进的同态滤波流程如图3所示。 图3 改进的同态滤波流程Fig.3 Diagram of new cepstral filtering 对不同麦克风的接收信号进行以上处理,然后用广义互相关法做延时估计。该方法既滤除了房间脉冲响应的最小相位部分,又能保留其全通部分和声源信号中的更多信息,可以使混响的影响大大降低,并能保证接收信号之间的相关性,减少了估计误差。 为了对以上提出的改进方法进行验证,本文首先仿真传统的时延估计算法,然后在同等条件下与新算法的处理结果进行对比,通过调整不同的混响时间得到数据,对结果做分析与说明。 本实验使用音乐厅作为仿真环境,房间尺寸(长×宽×高)为(10.0 m×10.0 m×3.0 m),利用房间的音质预测原理求出其房间回响模型[14],调整混响时间RT60控制混响声的强弱,假定房间内没有体积很大的杂物。从TIMIT语音库中选取一段语音“Thus technical efficiency is achieved at the expense of actual experience.”,采样频率fs为1 6 kHz。 假定室内是单一声源,位置固定,使用两个相同的全向麦克风来接收声音信号,它们的坐标分别为(5.00,4.90,1.00)和(5.00,5.10,1.00),根据传输模型得到两个接收信号,在两个接收位置接收的信号中分别添加高斯白噪声使接收信号的信噪比为20 db,模拟出实际无声环境,与按照以上模型求出的传输函数做卷积运算,模拟出实际接收信号xi(n)和xj(n),即构造了混响环境下加有特定高斯白噪声的两个接收信号。 声源位置为(2.00,4.00,1.80)时,接收信号的波形如图4所示。 (a) 实际接收信号A滤波后的时域波形 (b) 实际接收信号B滤波后的时域波形 考虑到数字滤波处理的精度高、稳定灵活,本文采用数字滤波的方式实现带通滤波。语音信号的频率范围是400~3 400 Hz,所以设置带通滤波的通带边界频率分别为400、3 400 Hz,过渡带的宽度设置为100 Hz,通带最大衰减Rp设置为5,阻带最小衰减As设置为20,实现数字滤波操作,滤波前后接收信号的幅频特性如图5所示。 (a) 滤波前接收信号的幅频特性 (b) 滤波后接收信号的幅频特性 图5 滤波前后接收信号的幅频特性 滤波后对接收到的信号进行加窗分帧操作,因为用离散傅里叶变换做谱分析会有截断效应的影响,而汉明窗的第一旁瓣衰减比较大,可以减小频谱泄露的影响,所以这里使用汉明窗。将普通的GCC和CEP-GCC算法作为比较对象,比较改进后的算法在不同的混响时间背景下的估计性能指标,观察其抗混响能力。 室内环境下的混响时间通常在0.3~0.7 s[15],所以设RT60分别为0.4、0.7 s时,每次将接收信号中所有有效帧求得的估计结果取平均,多次实验后得到不同算法对应的相关函数如图6所示,其横坐标表示相关函数在时间轴上的数值,纵坐标表示各算法对应的相关函数的取值。通过比较相关函数波形来分析各种算法的优势和不足。 (a) RT60=0.4 s GCC算法 (b) RT60=0.7 s GCC算法 (c) RT60=0.4 s CEP-GCC算法 (d) RT60=0.7 s CEP-GCC算法 (e) RT60=0.4 s 新算法 (f) RT60=0.7 s 新算法 对比图6可以看出,在混响时间为0.4 s时,GCC算法对应相关函数的峰值附近毛刺最多,且比较高;CEP-GCC算法对应的相关函数次之,新算法在峰值附近毛刺最小,也比较低。当混响时间增加到0.7 s,传统算法对应相关函数的毛刺明显增多,而新算法对应相关函数的毛刺增加不明显,依然比较低。 因为图6中相关函数过于密集,观察效果不够明显,这里根据麦克风之间的距离求出相关函数峰值检测的搜索范围,只对该范围进行搜索,这样既能减少运算量,又能更加精细地分析实验结果。搜索范围内的仿真结果如图7所示,其横、纵坐标和图6相同。 (a) RT60=0.4 s GCC算法 (b) RT60=0.7 s GCC算法 (c) RT60=0.4 s CEP-GCC算法 (d) RT60=0.7 s CEP-GCC算法 (e) RT60=0.4 s 新算法 (f) RT60=0.7 s 新算法 由以上结果可以看出,当混响时间为0.4 s时,3种算法都有比较尖锐的峰值,新算法对应相关函数的其他区域要更加平缓;当混响时间为0.7 s,在高混响条件下,GCC算法和CEP-GCC算法的主峰比较粗,且偏离了正确值,新算法虽然主峰有所加粗,但依然能保持尖锐的峰值,伪峰比其他算法要小,且峰值没有偏离正确位置。因此新算法的时延估计会有更加理想的效果。 接下来对不同算法得到的仿真结果做定量分析,本文使用以下指标作为估计性能的衡量标准: 异常点所占的百分比(percentage of abnormal point, PAP):实际时延对应的采样点和估计的采样点之差超过2个单位的估计样点为异常点。 均方根误差(root mean square error, RMSE),其值用ERMSE表示,计算方法如下: (21) 其中,N表示估计时延的总个数;τi是第i次估计得到的时间延时;τ指实际的时间延时。在本实验中,用采样点序号代替时间延时的值,用来统计实际值和测试值的偏离情况。 通过控制反射系数来得到不同的混响时间RT60对应的房间脉冲响应,在不同混响时间条件下进行多次实验,然后取平均结果。混响时间为0.1~1.0 s的不同算法估计性能统计结果如图8所示。 (a) PAP (b) ERMSE 图8 3种算法的PAP和ERMSE与RT60的关系Fig.8 Relationship between RT60 with PAP and ERMSE of three algorithms 由图8可以看出,在混响条件下GCC算法的PAP和ERMSE都比较高,CEP-GCC算法因为滤除了接收信号的最小相位部分,损失了声源信息,所以相关函数的相关性较低,PAP比较高,但ERMSE比较低,说明具有一定的抗混响性能;新算法因为保留了接收信号最小相位部分的大量声源信号,并滤除了房间脉冲响应的最小相位部分,既提高了抗混响性能,又保证了两路接收信号之间的相关性,其PAP和ERMSE都是3种算法中最低的。随着混响的加强,虽然PAP和ERMSE都呈现出上升趋势,但新算法得到的PAP和ERMSE依然低于前两种算法。可以看出本文提出的算法在混响干扰下,PAP比GCC算法降低了10%左右,在高混响条件下,ERMSE比GCC算法大约降低20%,比CEP-GCC算法大约降低8%,说明该算法在高混响条件下能更准确地估计出时间延时。 最后选择不同的声源位置,用3种算法分别估计选定位置对应的时间延时,对比各位置处的ERMSE,观察声源和麦克风相对位置对估计结果的影响。 设混响时间为0.5 s,考虑到空间位置的对称性,只在第一象限选择声源位置。设轴向角、仰角分别为0°、30°、45°、60°、90°,距离选择1.5、2.0、2.5 m,按照以上要求在空间选择出合适位置以反应轴向角、仰角和距离对估计结果的影响,各位置对应3种算法估计结果的ERMSE见表1至表3。 表1 轴向角和ERMSE的关系Tab.1 Relationship between axial angle and ERMSE 表2 仰角和ERMSE的关系Tab.2 Relationship between elevation and ERMSE 表3 距离和ERMSE的关系Tab.3 Relationship between distance and ERMSE 从表1至表3的对比可以看出,轴向角和仰角越接近90°,声源越接近于传声器连线的中垂线,因为理论时延值在减小,受时间分辨率的影响,时延估计的ERMSE越大;虽然本文提到的时延估计算法适用于远场模型,但如果距离过远,声音的衰减比较严重,ERMSE同样会增加。此外还能看出3种算法的ERMSE受其他干扰有波动,但总体上新算法的ERMSE比传统时延估计算法的ERMSE小。 综上,混响条件下新算法在时延估计中抗混响性能更强,时延估计的精度更高,表现更加优越。 本文根据同态滤波后接收信号相关性比较低的缺点,通过分析接收信号在倒谱域中的分布情况,提出了新的时延估计算法。该算法从接收信号的最小相位部分滤除了包含混响声的房间脉冲响应的最小相位部分,保留了声源信号中的大量信息,既克服了混响干扰,又能保证接收信号之间的强相关性,结合接收信号的全通部分求出接收信号之间的时间延时。仿真实验结果表明,该算法估计结果的均方根误差约比传统GCC时延估计算法降低了20%,比CEP-GCC算法降低8%,可以大大减弱混响对时延估计的干扰,对空间中不同的位置,其时间延时的估计误差都比传统的时延估计算法小,在混响环境中能更准确地估计时延。
3 实验





Fig.5 Amplitude-frequency characteristics of the received signal before and after filtering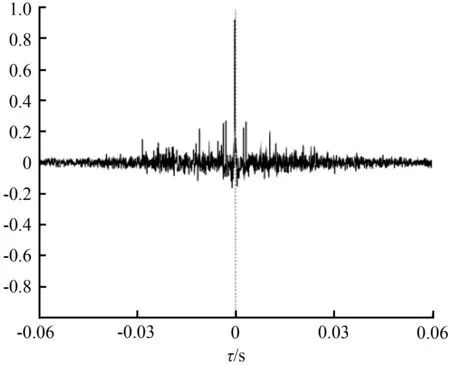















4 结论

