基于移动储能车的电网运行灵活性提升策略

(1.广西大学 电气工程学院， 广西 南宁 530004；2.广西电网有限责任公司 南宁供电局， 广西 南宁 530022)

0 引言

全球新增可再生能源装机容量在全球总新增装机容量中的占比持续增加。截至2019年，该比重已超过70%[1-2]。电网运行灵活性是指电网对可再生能源发电产生的大范围不确定性和波动性的应对能力[3]，被视为影响可再生能源消纳[2]和实现能源转型[3]的关键能力。本文认为，电网运行灵活性主要有以下两个方面：①具有足够的功率调节能力以跟踪净负荷曲线的变化；②具有足够的旋转备用容量以免疫净负荷不确定波动带来的影响。

尽管目前已有不少与电网灵活性相关的研究，但依然缺乏面向独立灵活性资源供应商的市场设计[4- 6]。在电力市场中，电力调度中心致力于整合电网中各类灵活性资源以应对可再生能源的波动性与不确定性，降低电网运行成本；而各灵活性资源供应商期望向电网提供的灵活性服务获得最大收益。如何为从电力调度中心到独立灵活性资源供应商等存在利益冲突的市场主体提供经济激励，并协调多方努力提高电网运行灵活性，增加社会福利，仍是一个有待解决的问题。

因此，本文以移动储能车运营商为例，其在具有价格信号的日前市场中调度移动储能车(mobile energy storage, MES)为系统提供灵活性辅助服务。移动储能车即为装载锂电池的电动卡车，具有时间和空间灵活性。为阐明动机，相关工作综述如下：

① 储能设备是集成大规模可再生能源，提高电网运行灵活性的关键[6]。高成本是阻碍其推广的主要障碍。但经过多年的发展，储能的成本大大降低[7],并有望在2030年降低75%[8]。多种储能技术已被广泛应用于提高电网在不同时间尺度下的运行灵活性：飞轮储能响应快，可用于实时电压和频率控制[9-10]；电池储能[11]可提高日内运行灵活性。文献[12]提出了一种考虑电力负荷季节差异的混合储能容量配置方法。此外，混合储能还被用于抑制电压波动[13]。

移动储能设备已被应用于提高电网弹性(power system resilience, PSR)[14-15]和提高极端天气下孤岛电网的供电能力[16-17]。此外，移动储能车还可用于提供调压和无功支撑服务[18]、吸收弃风电量[19]。鲜有将移动储能车应用于提升电网运行灵活性的研究。文献[20-21]将移动储能应用于电网调度。结果表明，移动储能可以缓解输电阻塞，削峰填谷，降低电网运行成本。但是，文献[20-21]用集中调度模型调度储能车，未将电网与储能车视为不同的利益主体。

② 多项技术已被用于应对新能源波动性[22]和提高电网运行灵活性[23]，但目前的市场结构仍然缺乏对灵活性产品和服务的投资激励[24]。为释放资源灵活性，美国加州电力系统运营商和中西部电力系统运营商推出了灵活爬坡产品(flexible ramping product, FRP)。FRP可以激励常规发电商和其他灵活资源供应商(需求响应、储能等)等市场参与者提供爬坡能力以跟踪净负荷波动、平抑可再生能源不确定性[25]。文献[26]运用电池储能提供FRP，但这项工作忽略了网络约束所造成的价格信号空间差异。

③ 价格信号反映资源的供需平衡状况，可为灵活资源提供经济激励。文献[27-28]研究了考虑调节性能的定价方法。文献[29-30]利用拉格朗日乘子的经济学解释，分别基于鲁棒优化和机会约束优化对电能和备用容量进行了定价。其中，节点边际电价(locational marginal price, LMP)和不确定性边际价格(uncertainty marginal price, UMP)[29]直观地量化了电网在时-空两个维度平衡电能供需和免疫不确定性的灵活性资源稀缺程度，可以用于电能和备用容量的定价。因此，本文以LMP和UMP激励储能车运营商参与电力市场，为电网提供电能和备用容量。采用主-从博弈模型协调电力调度中心和储能车运营商共同提高电网日前运行灵活性，并实现上述市场参与者的利益均衡。

1 电价制订和储能车建模

1.1 电力调度中心的定价策略

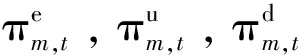
1.2 储能车建模

本小节将构建储能车调度模型，以基于上节推导的LMP和UMP最大化储能车运营商单个储能车的收益。多储能车及多运营商的优化策略将在第2章阐明。

所提模型与现有研究的主要区别有以下3个方面：①储能车由独立的运营商调度运行。储能车运营商之间、储能车运营商与电力调度中心之间均不共享参数信息。②模型考虑了储能车交通和备用约束。因此，储能车可以同时进行时间套利、空间套利、提供向上和向下旋转备用容量。③储能车运营商可同时获利于电价套利和销售旋转备用容量。

储能车调度模型 (mes dispatch, MD) 如下：

① 目标函数：

目标函数旨在最大化当前调度的储能车在电能套利和销售旋转备用容量的总收益：

(1)

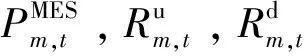
② 功率约束：

(2)

(3)

(4)

③ 电量约束：

(5)

(6)

(7)

公式(6)为储能车电量上下限约束，Emin，Emax分别为储能车存储的电量上下限；式(7)约束储能车在当前调度日的首末时段储电量一致。

④ 状态依赖约束：

(8)

(9)

(10)

(11)

公式(8)约束一辆储能车在一个时段内只能位于一个节点，αm,t为储能车的位置指标：

公式(9)约束储能车移动状态和并网运行状态互斥；公式(10)约束储能车充电与放电状态互斥；公式(11)约束储能车只有在并网运行状态下才能进行充放电操作。

⑤ 交通约束：

(12)

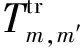
⑥ 旋转备用约束:

(13)

(14)

(15)

(16)

(17)

为响应LMP和UMP信号，储能车运营商会通过求解本节模型合理调度分配其储能车资源，向电网提供电能，向上/向下旋转备用，实现收益最大化。

另一方面，电力调度中心将致力于降低电网运行成本，它与储能车运营商存在利益冲突。下面将构造主-从博弈模型，使用电价信号沟通与协调电力调度中心和储能车运营商。

2 主从博弈模型与求解方法

2.1 电力调度中心与储能车运营商的主-从博弈模型

为了专注于应用储能车改善电网运行灵活性，本文做了以下假设：①为保证市场公平，价格信号对所有市场参与者公开，可以无延迟的被任意市场参与者获取。那么，所有储能车运营商作为市场参与者可以同时对价格信号做出响应并向电力调度中心提交运行策略。②假设所有储能车的性能相同。储能车性能差异的影响将在未来的研究中考虑。

基于上述假设，构建如图1所示的电力调度中心和储能车运营商的主-从博弈模型。主博弈方为电力调度中心，从博弈方为储能车运营商。主博弈方模型即为1.1中所述的定价模型。电力调度中心在考虑储能车提供的灵活性资源(电能与备用容量)的情况下，最小化电网日前运行成本，计算并下发LMP与UMP。从博弈方模型即为1.2节中提出的储能车调度模型。储能车运营商响应LMP和UMP价格信号，调度其储能车参与日前能量和辅助服务市场，并向电力调度中心上报运行决策。博弈双方相互影响和制约，他们都会根据对方的决策不断调整自身决策。市场将在双方的博弈均衡点出清。

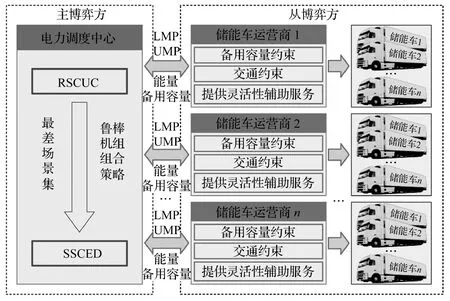
图1 电力调度中心和储能车运营商的主-从博弈模型Fig.1 Master-follower game model of ISO and MES owners

2.2 主-从博弈模型求解方法

本文的日前市场将以最后一辆储能车加入市场后的电价清算用户电费和所有参与电网运行的储能车的利润。因此，为求解上述主-从博弈模型，需要克服以下困难：

① 电价连续变化：在上述博弈模型中，储能车运营商的调度决策受市场电价影响，其调度决策也会影响市场电价：储能车运营商不简单的作为价格接受者。随着储能车向电网注入灵活性资源，市场电价也会随之变化以反映电网实时的供需平衡状态。这会增大求解博弈模型和获取市场均衡点的难度。

② 储能车的趋同性：趋同性是指在同一价格信号的引导下，所有储能车的运行决策都将趋于一致，以获得最大利润(例如，所有储能车都将于电价最高的时段前往电价最高的节点提供服务，获得最大利润)。储能车的趋同性相当于将多个储能车“捆绑”成一个大的储能车进行调度。这会忽略单辆储能车的加入对电网供需平衡的影响，造成某一时段某一节点的灵活性资源“过补偿”，不仅造成储能车灵活性损失，而且导致资源浪费，市场效率低下。

③ 储能车耦合： SSCED的网络安全约束使得在电网中运行的多辆储能车在整个主-从博弈模型中是耦合且相互影响的。储能车在任意时间和节点提供的灵活性资源都会改变潮流分布，影响整个电网的供需平衡和市场电价。因此，储能车会相互影响彼此的收益，进而影响储能车运营商的总收益。

为解决上述问题，采用以下解决方法：

① 设计了一个迭代算法来求解电力调度中心和储能车运营商之间的主-从博弈模型，并确定市场均衡。该算法步骤如下：a)电力调度中心求解无储能车的主博弈方模型并下发初始LMP与UMP;b)储能车运营商基于LMP/UMP求解从博弈方模型，并向电力调度中心提交运行决策。从博弈方模型的目标函数为储能车运营商的预期利润We;c)电力调度中心将储能车运营商提交的运行决策视为各节点上确定性的发电功率(储能车放电)或负荷(储能车充电)，并将储能车提供的备用容量用于抵消不确定性偏差，随后重新求解SSCED，更新LMP/UMP。电力调度中心可以根据更新后的实际电价计算储能车运营商的实际利润Wa。电力调度中心和储能车运营商之间交换的信息仅为LMP/UMP及储能车运行策略。重复步骤b)和c)，当储能车运营商的实际利润不再上升，市场电价不再下降时，即可认为达到博弈均衡。

② 针对储能车的趋同行为，提出了一种序列式的储能车调度方法，将电力调度中心和储能车运营商之间的博弈扩展到若干回合。每个储能车运营商在一个博弈回合之内仅能调度一辆储能车。例如，图2所示的储能车A1、B1和C1分别隶属于储能车运营商A、B和C，它们将在博弈回合1中被调度。剩余的储能车以此类推。另外，已调度的储能车的调度结果将作为调度后续储能车的边际条件。也就是说，下一博弈回合用于调度储能车的LMP和UMP是电力调度中心根据上一博弈回合的储能车调度结果更新的。因此，对于任一储能车运营商来说，其每一辆储能车使用的电价信号都是不一样的。这样就避免了同一储能车运营商的多辆储能车趋同和“捆绑”问题，从而充分利用其灵活性。

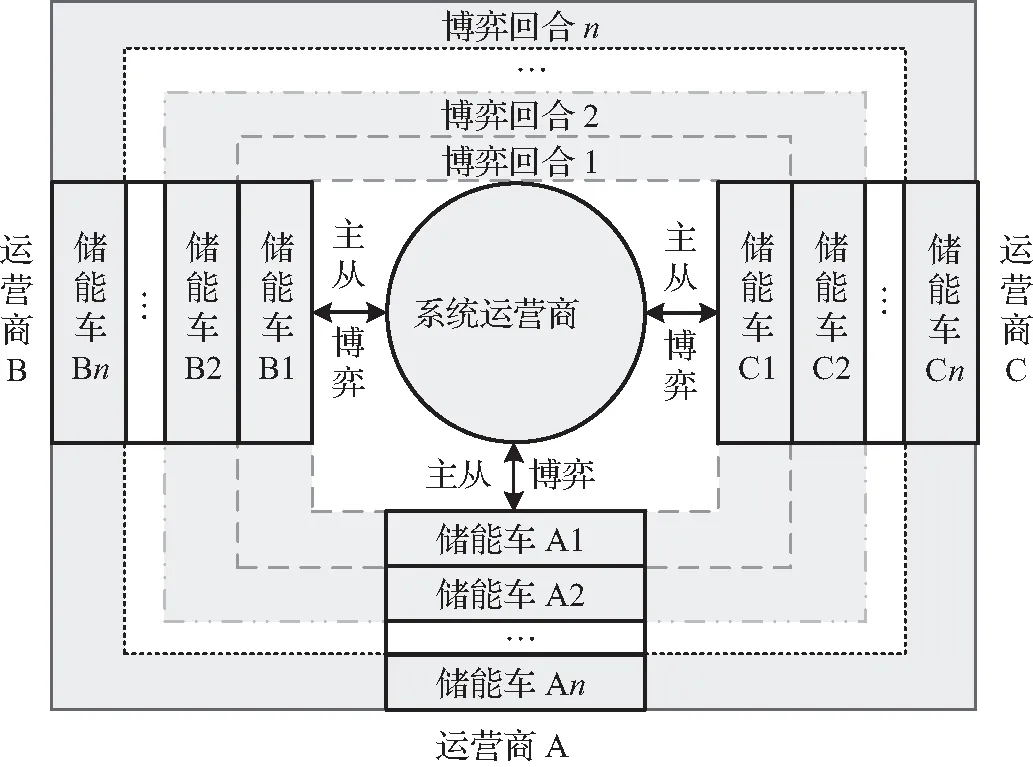
图2 序列式储能车调度方法Fig.2 Sequential MES dispatching method

③ 接下来解决储能车耦合问题。为了表述简洁，下面只描述一个储能车运营商的求解方案和求解算法，每个储能车运营商的解决方案都是相同的。任一储能车的运行策略一旦由博弈算法确定将无法修改，而电价却随着储能车的加入而不断变化。因此，对从博弈方模型的目标函数进行扩展，使其包含先前博弈回合被调度的所有储能车的运行决策：计算第n辆储能车的调度决策时，第1至n-1辆储能车的调度决策将作为固定参数逐回合添加到储能车调度模型的目标函数中。因此，储能车调度模型的目标函数将包含全部已调度的储能车的运行决策信息。即使电价变化，目标函数依然随迭代回合逐步更新以确保所有被调度储能车的总收益最大。因此，储能车运营商可以在考虑储能车之间相互影响的情况下最大化总收益。该调度策略如图3所示。

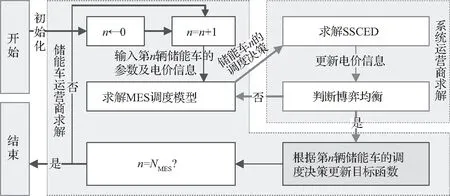
图3 储能车运营商的调度流程Fig.3 Dispatch process of one MES owner

综上，所提电力调度中心和单个储能车运营商的主从博弈模型的分布式迭代算法见算法1，该算法对所有储能车运营商都是通用的。

算法1: 主从博弈模型求解算法Step 1:求解RSCUC模型, 获得机组组合策略Step 2:求解无储能车的SSCED模型,获得初始电价信号πe(0)m,t, πu(0)m,t, πd(0)m,t, 令n←1, I←∅, 定义收敛间隙θStep 3:while n≤NMESdo令j←1,πe(n)m,t←πe(n-1)m,t,πu(n)m,t←πu(n-1)m,t, πd(n)m,t←πd(n-1)m,t, W(n,j)e←Big-M, W(n,j)a←-Big-MStep 4:while(W(n,j)e-W(n,j)a)W(n,j)a≥θ, doStep 5:更新储能车调度模型的目标函数: W(n,j)e=max∑t∑m(PMES(n,j)m,t+∑i∈IP(i)m,t)·πem,t+(Ru(n,j)m,t+∑iIRu(i)m,t)·πum,t+(Rd(n,j)m,t+∑iIRd(i)m,t)·πdm,tìîíïïïïïïüþýïïïïïï ∀m,t;Step 6:令πem,t=πe(n)m,t,πum,t=πu(n)m,t,πdm,t=πd(n)m,t, 求解储能车调度模型,得到PMES(n,j)m,t, Ru(n,j)m,t, Rd(n,j)m,t,以及预期利润W(n,j)eStep 7:令dm,t=d(n)m,t-PMES(n,j)m,t,km,t=k(n)m,t-Rk(n,j)m,t,∀k∈K,∀m,t;再次求解SSCED模型,得到πe(n,j)m,t,πu(n,j)m,t,πd(n,j)m,tStep 8:令πem,t=πe(n,j)m,t, πum,t=πu(n,j)m,t,πdm,t=πd(n,j)m,t,∀m,t,计算储能车实际利润W(n,j)a:W(n,j)a=∑t∑m(PMES(n,j)m,t+∑i∈IPMES(i)m,t)·πem,t+(Ru(n,j)m,t+∑i∈IRu(i)m,t)·πum,t+(Rd(n,j)m,t+∑i∈IRd(i)m,t)·πdm,tìîíïïïïïïüþýïïïïïï ∀m,tStep 9:πe(n)m,t←πe(n,j)m,t, πu(n)m,t←πu(n,j)m,t, πd(n)m,t←πd(n,j)m,tj←j+1, Step 10:end whileStep 11:PMES(i)m,t=PMES(n,j)m,t, Ru(i)m,t=Ru(n,j)m,t, Rd(i)m,t=Rd(n,j)m,t, d(n+1)m,t=(d(n)m,t-PMES(i)m,t),{k(n+1)m,t=(k(n)m,t-Rk(i)m,t),∀k∈K}, I=I∪n, n=n+1Step 12:end while

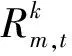
(18)

3 算例分析

采用IEEE 6-Bus系统、IEEE 118-Bus系统来验证所提出方法的有效性。算例在MATLAB平台求解实现。主从博弈的收敛间隙设定为相对误差1%。

3.1 IEEE 6-Bus 算例

① 算例参数设定

该系统包含3台发电机和7条输电线路。节点1含一个风电厂，节点4含一个光伏电站，它们具有不确定性。节点2和6接入常规发电机组，不含任何负荷。节点3和5接入确定性负荷。系统负荷曲线和可再生能源发电曲线如图4所示。节点1和4的净负荷不确定偏差上限见表1。

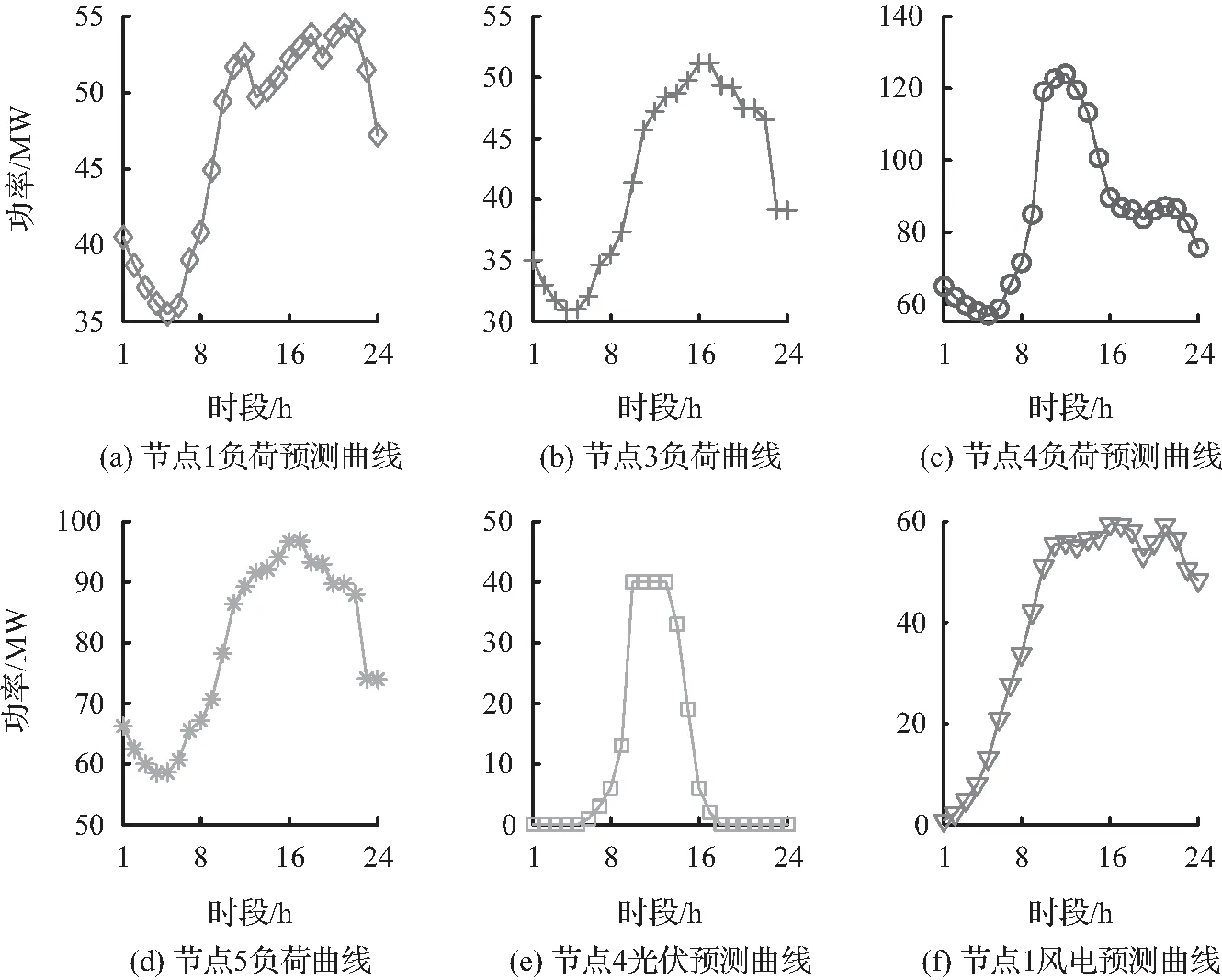
图4 IEEE 6-Bus系统可再生能源发电与负荷曲线Fig.4 Load and renewable generation curve of IEEE 6-Bus system

本系统考虑一个拥有4辆储能车的储能车运营商。表2列出了储能车参数。储能车在电网各节点间的移动时间见表3。

表1 节点1,节点4的净负荷不确定偏差上限Tab.1 Uncertain deviation bounds of net load of Bus 1 and Bus 4

表2 储能车参数Tab.2 Parameters of MESs

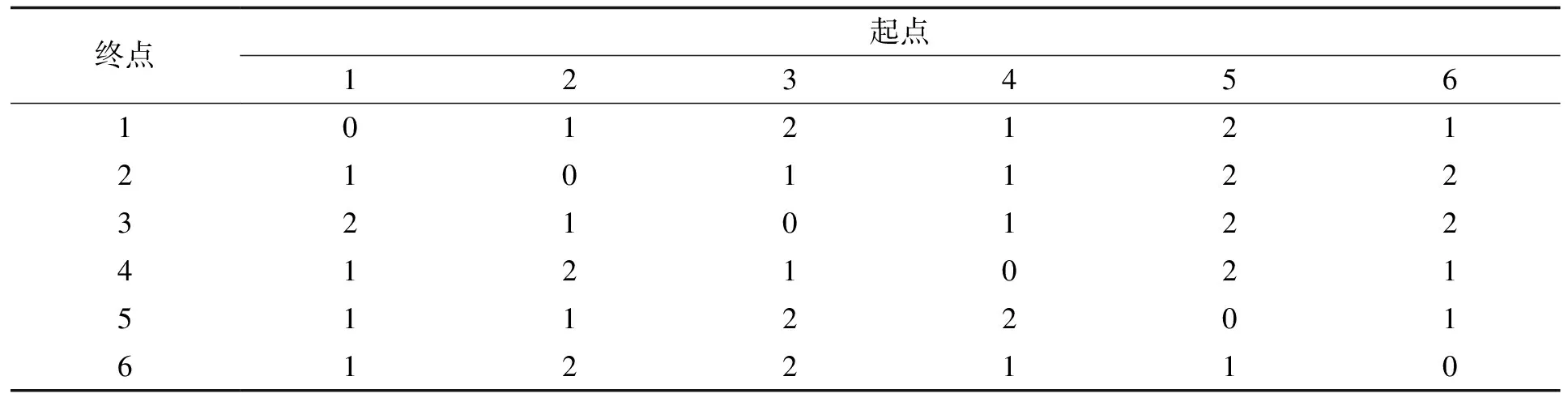
表3 储能车移动时间Tab.3 Travelling time of MESs 单位：h

② 无储能车的初始电价

根据系统参数，电力调度中心通过求解RSCUC和SSCED得到如图5所示的无储能车的初始LMP和UMP：

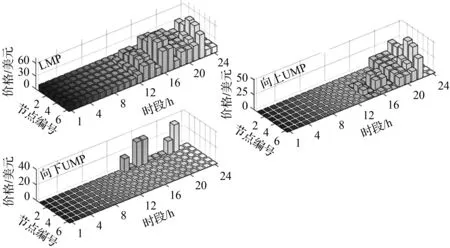
图5 IEEE 6-Bus系统初始电价Fig.5 Initial LMP and UMP of IEEE 6-Bus system

从图5可以看出，在22时段，节点4和节点5的LMP、向上UMP较高，意味着能量和向上旋转备用容量供应较为稀缺。而节点1在22时段的向下UMP较高，意味着向下旋转备用容量较为稀缺。另一方面，节点5仅含确定性负荷，其高LMP和向上UMP源于输电阻塞。

③ 储能车调度结果

根据上面的初始电价信号，储能车运营商可以使用所提出的方法对表2中的4辆储能车进行调度，为电网提供能量和备用容量。计算结果如下。

首先分析如图6所示的储能车的位置变化，方框内的数字表示位于相应节点上的储能车数量。时段为0的列表示储能车的初始位置。箭头为储能车的移动路径。图中所有储能车在3-4时段均移动至节点4。随后，它们在13-14时段陆续向节点1转移。节点4和节点1正是本例设定的具有不确定性的节点，因此该结果验证了所提方法能有效驱动储能车到需要运行灵活性的节点提供服务。

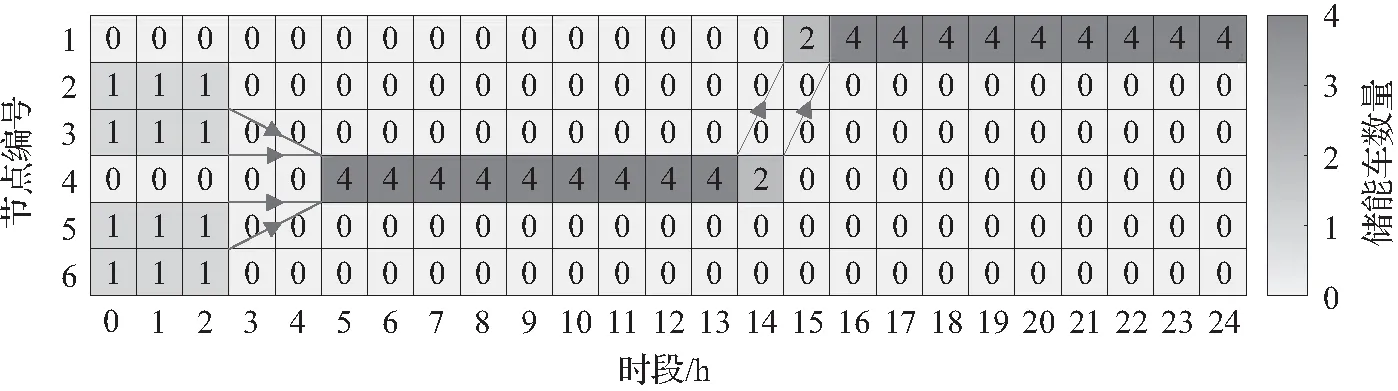
图6 储能车位置变化情况Fig.6 Locational changes of MESs

其次研究如图7所示的每辆储能车的具体充电策略。对比观察图7、图6和图5发现，储能车的运行策略主要分为两个阶段：①能量市场套利：在第11时段之前，大多数节点的LMP都较低，为14～15美元。但节点4在13时段的LMP却高达43.6美元。根据这一电价特征，储能车会提前在其他节点充满电，并于13时段移动到节点4放电，赚取能量差价。之后的时段储能车依然存在套利行为。②销售旋转备用容量：14-24时段，储能车主要通过在备用市场上出售旋转储备容量来获取利润。注意到仅节点1在19-22时段同时具有向上和向下UMP，且该节点在16、17和21时段的向下UMP均高于其他节点。因此，储能车将在13时段后移动到节点1，于16和17时段向其销售向下旋转备用容量；于19-22时段同时销售向上和向下旋转备用容量，赚取利润。

接着对比储能车加入前和加入后的市场电价，分别如图5和图8所示。储能车参与电力市场，提供灵活性资源后，LMP和UMP显著降低(尤其是22时段)，这说明：①灵活性资源的供应由稀缺变得充足，电网对灵活性资源的需求降低；②电网运行成本降低；③储能车有效提高了电网的经济性和运行灵活性。

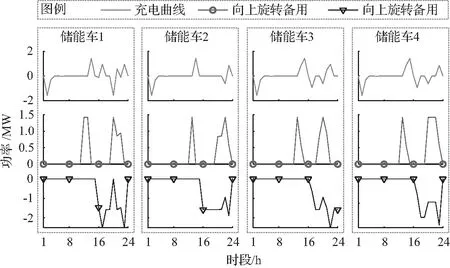
图7 储能车充电策略Fig.7 Charging strategies of MESs

最后研究如图9所示的电力用户电能支出和备用容量支出(能量和备用容量支出定义为节点负荷量和备用容量分别乘以相应的LMP和UMP)及储能车运营商的利润变化情况。可见，随着电网中储能车数量的增加，用户的电能和备用容量支出均减少，而储能车运营商的利润不断增加。这意味着：①消费者的用电成本降低，②储能车运营商提供的灵活性服务在市场中已得到合理出清。

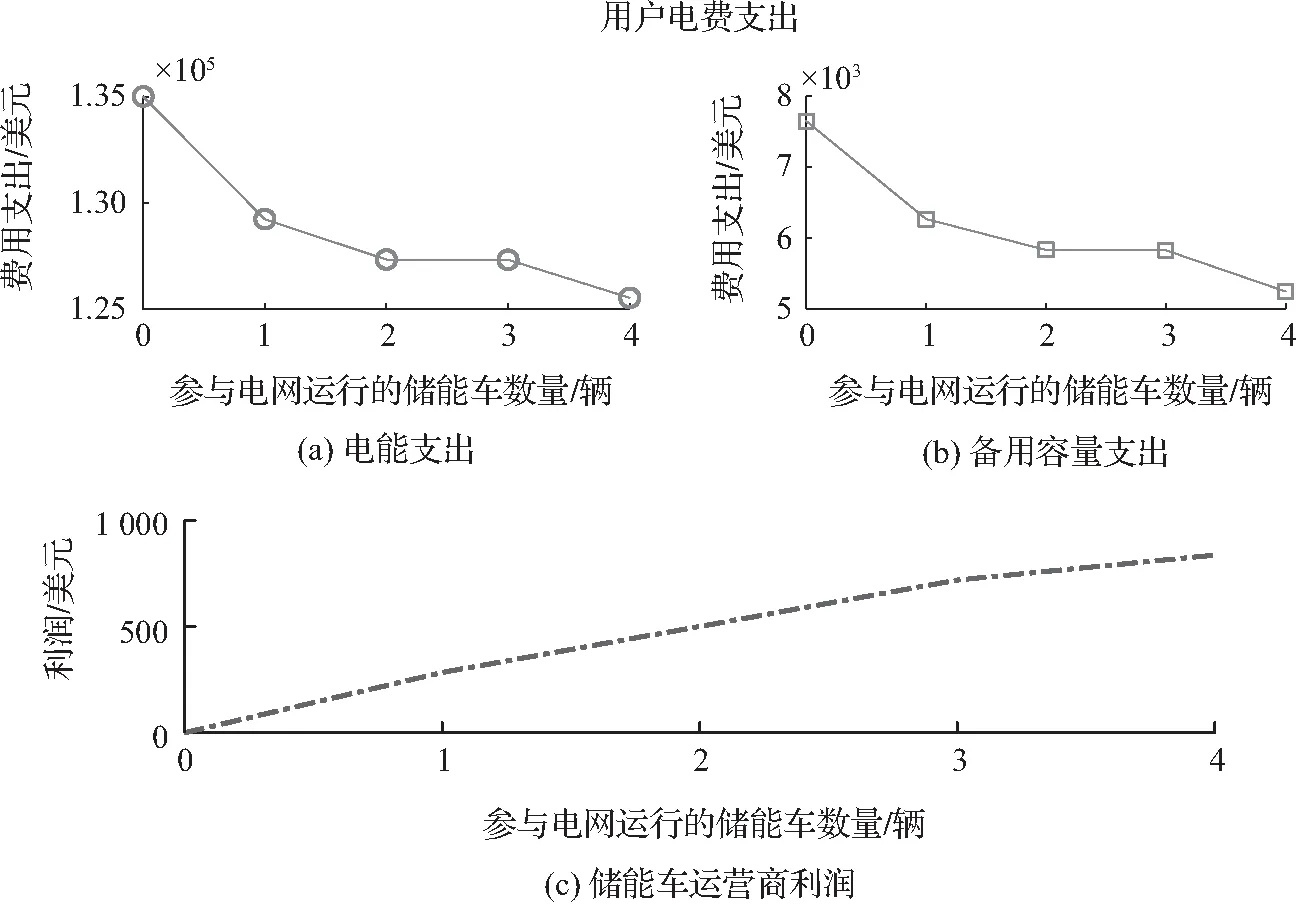
图9 IEEE 6-Bus系统电力用户费用支出及储能车运营商利润曲线Fig.9 Electricity user’s payments and MES owner’s profit curve of IEEE 6-Bus system

此外，用户的电能和备用容量支出分别下降9 519.82美元和2 404.44美元，而储能车运营商总利润为836.54美元。降低的电费远高于储能车运营商获得的利润，社会福利得到了极大提升。

从以上分析可以看出，采用所提出方法调度的储能车能够有效提高电网运行灵活性，实现电网、电力用户和储能车运营商的“三赢”：电网运行成本降低；电力用户的用电支出降低；储能车运营商获得合理利润。

此外，图9显示，电力用户的电能和备用容量支出呈非线性下降。某些储能车(如储能车1)的加入会导致市场价格急剧下跌。但另外的一些储能车(如储能车3)的加入仅造成市场电价的轻微下跌。该问题将于下一算例进一步研究。

3.2 IEEE 118-Bus 算例

① 算例参数设定

在本例中，节点15、49、54、59和80各接入一个风电场，它们是不确定性节点。这些节点的净负荷曲线由节点59的净负荷曲线缩放0.31至0.47倍得到，且它们的不确定偏差上限设为它们在相应时段的净负荷值。除上述节点外，其余常规节点的净负荷特性由节点11的净负荷特性缩放0.03到1.17倍得到。节点59、节点11的净负荷曲线，节点59的风力发电预测曲线如图10所示。

图10 IEEE 118-Bus系统的负荷与风电出力曲线Fig.10 Loadcurves and wind power curve of 118-Bus system

为深入分析IEEE 6-Bus算例末尾所提出的问题，本例考虑一个拥有10辆额定功率15 MW，最大储电量30 MWh储能车的储能车运营商。为使结果更具说服力，本例将储能车初始节点与系统不确定性节点间的移动时间设置为2 h，其余设置为1 h。储能车每小时交通能耗增大为150 kWh。

② 计算结果分析

通过计算得到图11所示的结果。首先，采用本文方法调度的储能车仍有效提高电网的经济性、运行灵活性和社会福利。此外，用户的电能和备用容量支出也呈非线性下降趋势：随着第1、4号储能车的加入，用户的电能和备用容量支出均明显下降，但其他储能车的加入仅轻微降低用户支出。

图11 IEEE 118-Bus系统电力用户费用支出及储能车运营商利润曲线Fig.11 Electricity user’s payments and MES owner’s profit curve of IEEE 118-Bus system

储能车加入后，电网边际机组(满足最后一单位负荷需求的发电机组，其机会成本等于市场价格)能否由昂贵机组切换为经济机组，是影响电价下降的关键因素。以下用LMP为例说明，UMP可用相同方法论证。

LMP主要由边际发电成本(λ)决定，即边际机组的发电成本。由于不同发电机组的发电成本曲线通常差别很大，一旦边际机组由一台切换至另一台，λ也会发生显著变化。相反，若储能车的加入没有改变边际机组，λ只会随着当前边际机组出力的变化而轻微变化。

表4列出了本例中λ在10，12时段随储能车3-5逐步加入的变化情况。可以看出，λ在第10和12时段，第4辆储能车进入电网时，电价分别由27.035 7 美元/MWh和27.265 9 美元/MWh骤降至20.112 8 美元/MWh和20.098 5 美元/MWh，降幅最大达到7.167 4 美元/MWh。而在其他时段其他储能车进入电网时，最大降幅仅为0.152 8 美元/MWh。λ的大幅下降意味着储能车4的加入使得电网在10、12时段的边际机组由原本的昂贵机组切换为更经济的机组，电网运行成本、市场电价、用户的电费也会随之降低。另一方面，λ的轻微下降说明储能车的加入仅影响了当前边际机组的出力大小，仅轻微降低电网运行成本、市场电价和用户电费。另外，由于市场将以最后一辆储能车加入市场后的电价清算用户电费和所有参与电网运行的储能车的利润，电价的大幅下降也会减少已调度储能车的利润。若此时电网中已有多辆储能车正在运行，电价的骤降将影响所有已调度储能车的利润，进而影响储能车运营商的总利润。这也是图11中储能车运营商的利润在第4辆储能车的加入时反而有所下降的原因。

表4 λ随储能车逐步加入的变化情况Tab.4 λ changes with the gradual addition of MESs 单位：美元

以上分析可以看出，储能车是密切相关的。后调度的储能车会影响市场电价进而影响之前已调度储能车的利润。因此，提出的目标函数更新策略考虑了储能车之间的相互影响，确保储能车运营商在所研究的时间范围内获得最大的全局利润。

4 结论

为提高含可再生能源电网的运行灵活性，本文使用市场手段激励独立储能车运营商参与提高电网运行灵活性。所做工作总结如下：首先，将LMP和UMP用于量化电网对灵活性资源的需求；其次，建立了储能车响应电价信号，向电网提供多种灵活性资源的调度模型；最后，提出一种主-从博弈模型与迭代算法以求解灵活性资源的供需平衡，出清灵活性辅助服务市场。

通过上述工作发现：①LMP和UMP在时间和空间两个维度反映电网对灵活性的需求，可以引导储能车到需要灵活性的节点。②储能车运营商根据LMP和UMP信号将储能车的资源合理分配给能量和备用服务。储能车更愿意通过响应UMP来提供备用容量。③储能车提供的灵活服务带来三赢的局面：电网运行灵活性得到提高，运行成本下降；电力消费者减少了用电支出；储能车运营商获得了利润。所提方法实现了社会福利显著提升。

后续研究将差异化储能车的性能参数，研究储能车运营商的竞争情况。同时，提出的方法将应用于协调其他不同特性的灵活资源。