基于机器学习的气体传感器数据处理算法解析

辛忠洋

（中国移动通信集团山东有限公司济宁分公司，山东 济宁 272000）

1 什么是气体传感器数据

作为对气体进行检测的技术之一，机器嗅觉可被拆分成两部分，分别是对传感数据进行采集、对采集数据进行处理，其中，对系统输出起决定作用的环节为数据处理。气体数据是指气体传感器以阵列为依托，通过长期收集所得到数据。对数据进行收集期间，相关人员应对压力、温度等外部环境严加控制。

对气体数据加以表示所用音频及图像数据，通常有显著差异存在，相关人员考虑到气体数据的获得途径是阵列采样，故提出用以下公式对数据样本进行表达：

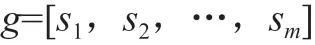
式中，si为数据特征i；m为特征数量。由此可见，要想使特征数据集得到准确表示，可采用以下公式：

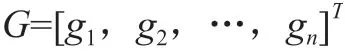
式中，gj为样本数据j；n为样本数量。要想使机器学习算法取得符合心理预期的良好分类效果，关键是提前处理气体数据。对诸多因素加以考虑后，相关人员提出以下处理策略：一是数据标准化，二是PCA。其中，PCA需要尤为注意，作为着重分析主成分的技术，PCA强调以降维思想为指导，确保单指标能够被有效转变成综合指标。

2 机器学习算法解析

2.1 建立模型

2.1.1 评价指标

对回归模型进行评价的指标，主要有MSE、MAE和RMSE，其中，对MSE进行计算的公式为：

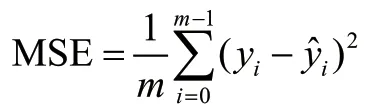
由上述公式可知，该指标强调先对真实值、预测值进行减法计算，获得偏方后，再对平均值进行求解。由于回归模型的损失函数多为MSE，这也表明在预测环节将MSE视作评价指标有实际意义。

对MAE进行计算的公式为：

作为线性分数的一种，MAE的特点是个体误差对应平均值有相等权重，即：个体误差均要接受线性惩罚。上文提到的MSE和下文即将介绍的RMSE，其误差惩罚均为非线性惩罚，这点较易被忽略。

RMSE是以MSE为基础所进行的开根计算，其公式为：

如果数据有偏大的数量级，将有一定概率出现较高平方误差，对MES进行开根计算，可保证误差结果与数据始终处于相同数量级。

2.1.2 人工神经网络

将ANN和回归问题相结合，损失函数往往为MSE，要求相关人员以梯度下降法为依托，对模型进行优化训练。除特殊情况外，网络输出层均不对激活函数加以使用，这是因为预测数值范围有一定概率出现超出常用值域范围的问题，进而使预测计算无法更进一步。对人工神经网络进行训练较易出现过拟合情况。基于ANN所展开训练可被划分到监督学习阵营，要想使训练效果达到预期，关键是要有充足的标签样本提供支持。本文所研究气体传感器相关数据，通常要经过数年的收集或累积，可被用来辅助训练展开的样本数量有限，对网络进行训练的难度不言而喻。要想使上述问题得到解决，关键是以实际情况为依据，通过提前终止或是数据增强等方法，确保过拟合问题可得到有效预防[1]。

2.1.3 支持向量机

回 归 数 据 集 固 定，通 常 是T={（x1，y1），（x2，y2），…，（xN，yN），}，其中，xi的取值范围是Rn，i的取值范围是1至N。相关人员希望能够得到取值与y相近的回归模型：

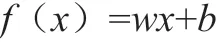
在该模型中，w、b均属于模型参数。常规回归模型用来展开损失计算所依托对象，通常以真实值、模型输出值为主，只有二者数值相等，才能得出损失是0的结论。本文所讨论支持向量机的特点，则是能够容忍二者有误差ε存在，只有二者误差较ε更大时，才会对损失进行计算。

基于支持向量机所建立回归模型、分类模型，在优化问题的处理方面，通常会采取相同的方法，即：先借助拉格朗日乘子将优化问题转变成对偶问题，再对问题进行解答。求解时，相关人员可根据实际情况决定是否用核函数对内积进行替代，确保特征能够得到自低维至高维的有序映射。但要注意一点，计算对象首选低维，这样做可降低计算难度，保证计算准确。

2.2 实验分析

2.2.1 实验说明

相关人员出于对比不同算法所取得分类效果的考虑，决定以前人研究所得气体传感器相关数据为依据，通过随机挑选的方式，确定本次实验所需乙醇样本，共600个，样本的乙醇浓度在10至600间。将乙醇样本平均分成3组，每组的样本数量为200个，仅对第1组样本进行训练，剩余两组作为测试组。为确保实验有实际意义，相关人员还制定了以下对比方案：方案1，仅利用Z-score对数据进行处理。方案2，在利用Z-score进行处理的基础上，借助PCA完成降维与特征提取操作。

2.2.2 人工神经网络

在参数过多的情况下，ANN有一定概率出现过拟合情况。而较多的网络层数所带来的问题，通常是梯度消失。对诸多因素加以考虑后，相关人员提出以隐藏层数量为一个的网络为依据，对回归任务进行落实，将该网络隐藏层共设128个神经元并接入ReLU，用来对函数进行激活，输出层则不对激活函数加以使用。另外，相关人员还计划通过提前终止的方式，对过拟合问题进行控制。本次实验的结果如下：

表1 回归结果

由实验结果可知，基于人工神经网络所建立回归模型，对方案1加以使用，通常可取得较为理想的效果，简单来说，就是凭借Z-score处理特征数据。这表明PCA降维所造成影响，往往集中在特征表达领域，方案2优势的发挥自然会受到制约。

2.2.3 支持向量机

相关人员出于对传感器数据所存在联系进行准确表达的考虑，决定利用径向基函数完成回归实验，借助网格搜索法，对C和gamma的最优值加以确定，作出这一决定的原因，主要是径向基函数有极强的映射能力。表2为网格搜索结果。

表2 不同方案的最优超参数

相关人员可借助最优超参数，基于不同方案分别训练第1组数据，将R2视为评价回归结果的核心指标，对比其他组数据，得出表3的结果。

表3 回归结果

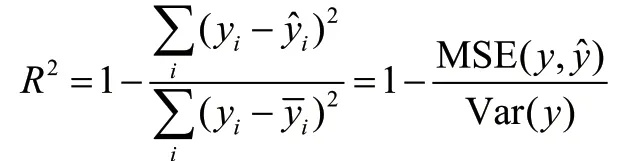
对上述计算公式进行分析能够发现，R2≤1，这表明R2的取值越靠近1，模型效果越理想，如果R2=1，则表明当前预测结果无误差存在，若R2=0，该模型则具备成为基准模型的条件。这里提到的基准模型，主要是指并未对特征取值加以考虑，而是以样本均值为依据，对预测值加以确定的模型。由此可见，将R2视为评价模型质量的指标，即便评价对象不同，最终结果仍有实际意义。

结合表3所给出数据可知，方案2所取得回归效果较方案1更符合预期，这表明基于PCA做降维处理，可使支持向量机效果得到优化，对气体样本相关特征进行提取时，同样可选择引入PCA降维，为回归精度提供保证。

2.2.4 比较分析

上文分别分析了基于不同算法所进行实验的结果，从不同维度对上述方法进行分析可得出以下结论：其一，将方案2与支持向量机结合，可获得最接近预期的回归效果。其二，将方案2与ANN结合，其回归效果往往差强人意。其三，基于方案1所展开实验的效果和方案2相反。从全局视角来看，相关人员所采取方案并不会给最终效果带来决定性影响，即：支持向量机所取得效果，均较人工神经网络更接近理想水平。

现将本次实验所得到结论归纳如下，供相关人员参考：首先是对气体浓度回归而言，支持向量机所取得效果明显较人工神经网络更符合实验要求。其次是PCA降维与网络特征表达的关联十分密切。最后是PCA降维+Z-score的组合，在多数情况下，均可被用来对气体浓度进行准确预测。

3 结束语

持续发展的机械嗅觉技术，现已被应用在航天航空、食品安全还有环境检测等领域，作为组成机器嗅觉不可缺少的部分，识别气体浓度的重要性有目共睹。本文着重讨论了如何利用机器学习对气体数据进行处理，通过实验分析的方式，对不同算法所取得效果进行对比，并得出可使效果最接近预期的算法，即逻辑回归+人工神经网络。