晶圆片盒传输机械手设计与运动仿真

万喜新，周益华，曾裕民，王学仕

(中国电子科技集团公司第四十八研究所，长沙 410111)

0 引言

在半导体集成电路产业中，立式扩散炉是生产线前工序的重要工艺设备。晶圆传输机构作为该设备的关键部件，主要负责在紧凑空间内对晶圆或装载晶圆的片盒，在不同工位之间完成精确定位且平稳高效的传递[1]。随着晶圆的尺寸规格及产能不断提升，对晶圆传输机构的精度、效率及稳定性提出了更高的要求，众多国内外学者对此展开了研究。

龚永佳[2]设计一种位姿可调的晶圆传输机械手平台，通过运动仿真分析，验证其能实现更高的传输效率及稳定性。谢均宇等[3]对机械手的多个动作过程进行优化调整，提高晶圆传输效率。但上述研究的机械手结构较简单，且均未出现运动逆解多解的情况。张昊等[4]采用自适应混合遗传算法结合5次均匀B样条插值方法，以提升晶圆传输机械手的运动平滑性，但该研究只针对轨迹进行平滑优化，而并未分析定位误差。

本文设计一种用于立式扩散炉中晶圆片盒传输的混合型机械手，并进行运动学正逆解分析。采用目标优化函数与PSO算法结合的方法寻优逆解，通过仿真实验，对机械手工作空间进行分析并验证最优逆解的定位精度。

1 三维模型结构设计

利用SolidWorks软件设计了晶圆片盒传输机械手的三维模型，如图1所示。

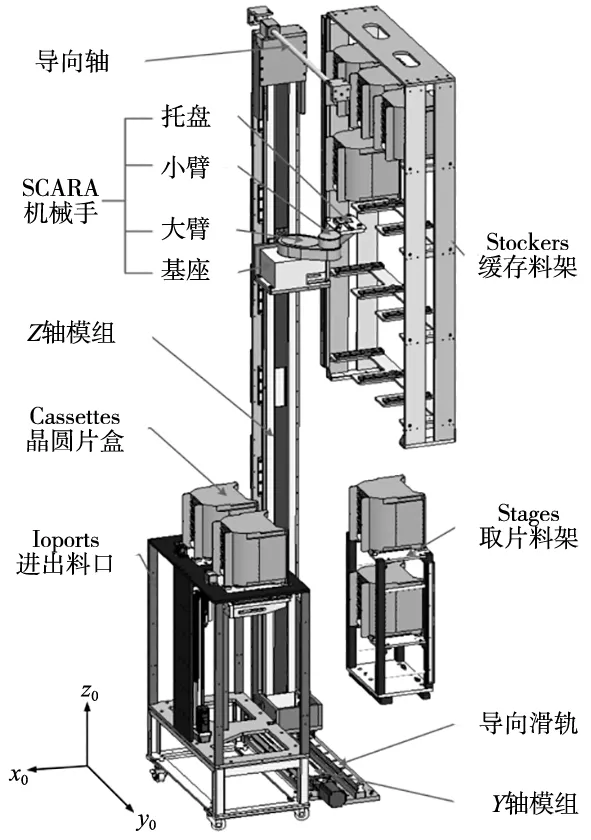
图1 晶圆片盒传输机械手三维模型

为实现晶圆片盒从进出料口到缓存料架、取片料架各工位之间的传输，将机械手主体结构设计成由Y、Z轴方向模组和SCARA机械手三大部分组成，共有2个移动关节和3个旋转关节。其中，Y轴模组水平固定于设备机架内的底板上，Z轴模组与Y轴模组的滑块连接固定，即Z轴模组可沿着Y轴方向水平直线移动；同时，考虑到Z轴模组整体长度达2.5 m，其质心距离地面较高，为保证其按照预定方向正常运动作业，通过在顶部和底部分别设置导向轴和导向滑轨，在一定程度上承载由运动引起的扭转、惯性力矩，使其运行过程保持平稳。

SCARA机械手的组成部件为基座、大臂、小臂、腕部及末端执行器(片盒托盘)。基座固定于Z轴模组的滑块上，其在Y-O-Z平面内的位置由两模组决定；末端执行器的工作范围、姿态则分别由主关节(大臂与小臂)、次关节(腕部)来调整控制。

最终通过Z轴模组、Y轴模组及SCARA机械手之间的协调运动，实现对晶圆片盒的托举、平移及转动。

2 运动学理论分析

2.1 改进型D-H法建立坐标系

改进型D-H法是建立机械手运动学模型的常用方法，利用4×4齐次变换矩阵，来表示相邻连杆之间的空间位置变换关系[5]。

为确定该五自由度传输机械手各连杆之间的相对运动关系，根据改进型D-H法绘制关节连杆坐标系如图2所示，并用四个参数对连杆进行描述：

(1)关节角θi，其值为轴xi-1变换到xi时需绕zi的旋转角度，沿逆时针方向为正；

(2)偏置di，其值为沿轴zi方向从xi-1平移到xi的距离；

(3)扭角αi-1，其值为轴zi-1变换到zi时需绕xi-1旋转的角度，沿逆时针方向为正；

(4)连杆ai-1，其值为沿轴xi-1方向从zi-1到zi的公法线距离。

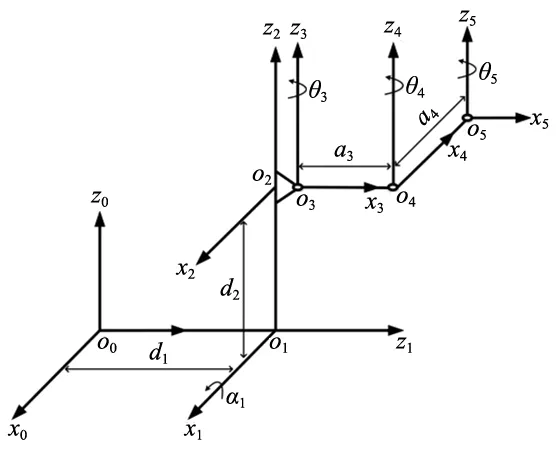
图2 晶圆片盒传输机械手连杆坐标系

通过分析图2可确定晶圆片盒传输机械手的D-H参数，如表1所示。

表1 晶圆片盒传输机械手D-H参数表

(1)

式中，cθi=cosθi，sθi=sinθi；cαi-1=cosαi-1，sαi-1=sinαi-1。

2.2 运动学正解

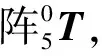
(2)

式中，c3=cosθ3，s3=sinθ3；c34=cos(θ3+θ4)，s34=sin(θ3+θ4)；c345=cos(θ3+θ4+θ5)，s345=sin(θ3+θ4+θ5)；a3=130 mm，a4=130 mm。

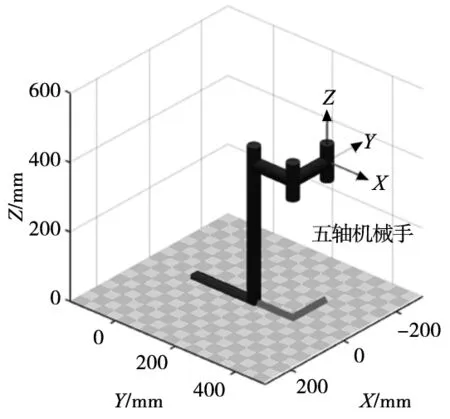
图3 机械手简易模型

(3)

可知计算结果唯一并且与图3中的末端位姿状态相符合，表明该运动方程学正确。

2.3 运动学逆解

机械手的运动学逆解问题则是指定末端执行器的目标位姿及各连杆参数，求解其对应的一系列关节变量值[7]。在求逆解过程中，首先可利用封闭解法求解，若存在该方法不能求出的逆解，可利用遗传算法或PSO算法等进行最优解求取。已知的末端位姿矩阵与各关节变量之间存在以下关系式：

(4)

式中，n、o、a为描述末端执行器位姿的3个单位矢量，分别是法线矢量、方向矢量、接近矢量；p为位置矢量。

令式(4)左右两边矩阵对应元素相等，得到：

(5)

根据晶圆传输机械手的实际工作要求，传输的晶圆片盒的姿态保持一个方向不变，只改变其空间位置，故要求SCARA机械手的三个关节角θ3、θ4、θ5具备以下关系：

cos(θ3+θ4+θ5)=1⟹θ3+θ4+θ5=2nπ (n=0,±1)

(6)

因此，该机械手的逆解问题简化为4个关节变量的逆解问题。

再分析式(5)，关节变量d2可直接解出，但d1、θ3、θ4在关节变化范围内存在无数种变量组合可实现末端执行器的位姿。

针对逆解存在无穷解的问题，本文通过构造目标优化函数，并利用PSO算法进行寻优求解。

(1)构造目标优化函数。

目标函数的构造原则是以满足目标位姿精度要求作为约束条件，以最小关节变化量(能耗最少)为优化目标。通过惩罚函数法可将上述约束优化问题转变成无约束问题后再求解，表示为：

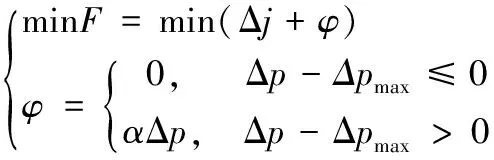
(7)

(8)

式中，F、φ分别为惩罚适应度函数、罚函数；Δp表示机械手末端执行器到达的实际位置pr与目标位置pd之间的差值，Δpmax为允许的最大位置误差；Δj表示末端执行器从起始位置运动到实际位置时，三个关节变量d1、θ3、θ4的变化值之和；α、β分别为惩罚系数和关节权值。

(2)PSO算法原理

PSO算法是一种利用粒子种群模仿鸟类个体间相互合作竞争的群体智能优化方法[8-9]，算法原理可描述为：在d维搜索空间中随机初始化一个种群，共包含N个粒子；在寻优搜索的迭代过程中，记录任意某个粒子的当前速度和位置，记为Vi=[vi1,vi2,…,vid]T和Xi=[xi1,xi2,…,xid]T，同时每个粒子根据个体极值和全局极值，记为Pi=[pi1,pi2,…,pid]T和Pg=[pg1,pg2,…,pgd]T，来更新速度和位置。第i个粒子的第d维速度与位置采用下式进行更新：

(9)

式中，j、jmax分别为当前、最大迭代次数；w为惯性权重，控制算法的全局、局部寻优能力；c1、c2为加速因子，通常根据经验值取2；r1、r2为分布于[0,1]之间的随机数，以增加搜索随机性。

3 运动仿真试验

3.1 工作空间分析

机械手工作空间是指其末端执行器在空间中的运动工作范围，可用所能到达的空间点集合来表示。工作空间是评估机械手性能的关键指标，对其进行研究分析具有重要意义。

蒙特卡洛法作为工作空间的分析方法之一，能快速直观地在计算机中模拟真实的物理过程[10]。本文基于MATLAB平台进行编程，求解晶元片盒传输机械手工作空间的具体步骤如下：

(1)利用函数rand(1,N)生成N个0～1之间的随机数，代入下式可实现在关节变量范围内进行随机遍历取值。

(10)

式中，i=1～5，dimin，θimin表示关节变量的下限值，dimax，θimax表示关节变量的上限值。

(2)将上述步骤得到的所有关节变量值代入运动学方程中，求得末端执行器位置向量p的集合，即机械手的工作空间范围。

N取值越大，越能准确描绘机械手工作空间，但计算耗时将增加，故综合考虑令N=15 000。利用MATLAB仿真运算，得到晶元片盒传输机械手在笛卡尔坐标系中的工作空间点集云图，如图4所示。

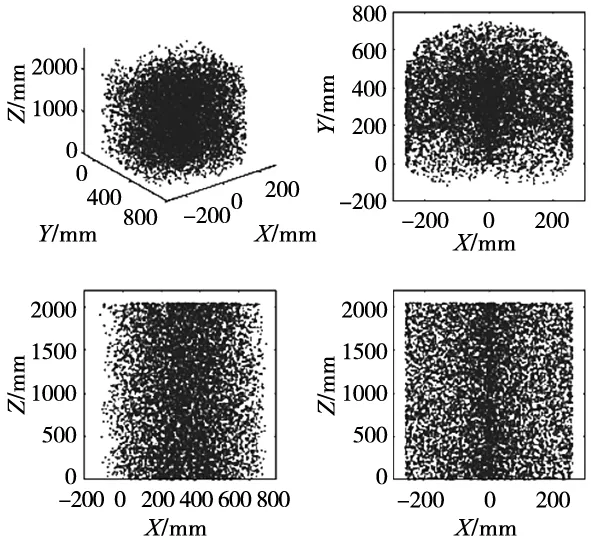
图4 晶元片盒传输机械手工作空间云图

观察云图可知，机械手在x轴方向的可达范围为[-260 mm,260 mm]，在y轴方向为[-130 mm,750 mm]，在z轴方向为[0,2050 mm]。整个晶元片盒传输机械手的工作空间是一个横截面近似心形的柱体，且结构紧凑，无明显空穴，能够覆盖该传输机械手的工作区域范围，满足片盒搬运的工作要求。

3.2 PSO算法逆解寻优

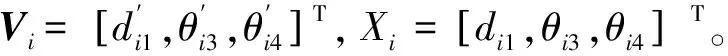
给定末端执行器在工作空间中的目标位置为pdx=200 mm，pdy=400 mm；起始关节变量值为jini=(0,0,π/2,-π,π/2)，定位精度要求Δpmax≤0.2 mm。

设置种群规模N为20，最大迭代次数为100，惯性权重w取0.8；通过MATLAB平台进行编程，对逆解进行优化迭代计算，得到如图5所示的PSO算法逆解寻优适应度曲线图。

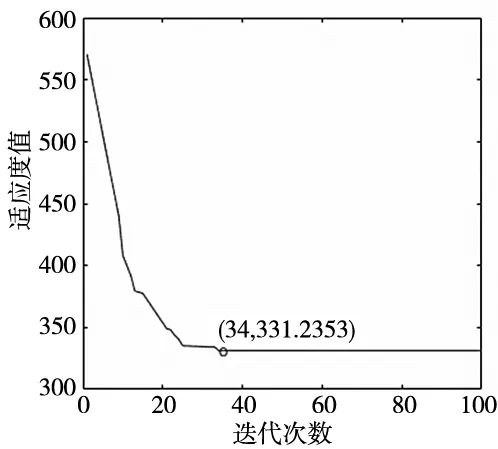
图5 逆解寻优适应度曲线图

图5中的横轴为粒子种群迭代次数，纵轴为每代的适应度值，折线上的点代表每一代粒子种群的最佳适应度。从图中可知，最佳适应度随着迭代次数逐步增加，表明其未陷入局部极值；当种群迭代34次后得到最优解。

在工作空间中选取3个目标坐标，通过PSO算法解出各关节变量最优解，并代入运动学方程中计算实际坐标，得到如表2所示的逆解寻优结果。

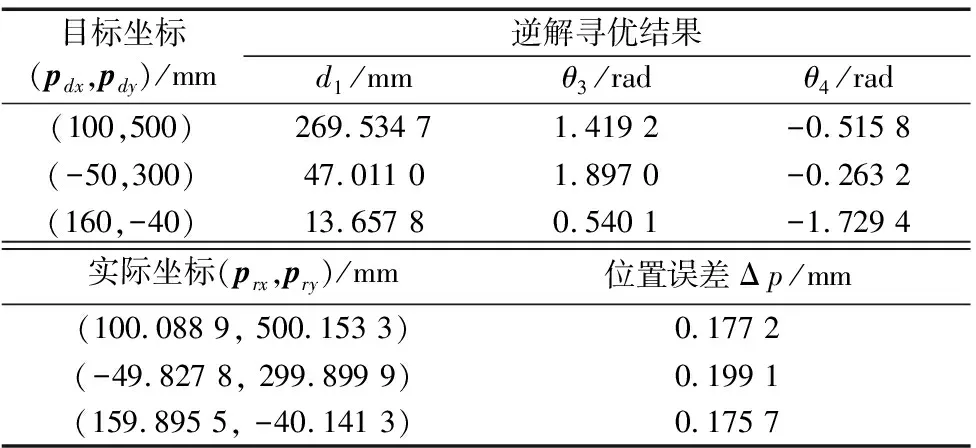
表2 PSO算法逆解寻优结果

从表2中可以得知，实际坐标点与目标坐标点的位置误差均≤0.2 mm，因此运用PSO算法求得的最优逆解能够满足设定的定位精度要求。

3.3 连续运动轨迹测试

令目标位置pdx=200 mm，pdy=400 mm，由上述起始关节变量值jini可知初始位置pinix=0 mm，piniy=0 mm。

在起始位置到末端位置之间通过Robotics Toolbox中的插值函数计算得到10个连续运动轨迹点，再运用PSO算法求得对应的10组最优逆解，并绘制如图6所示的逆解曲线图。

观察图6可知，连续运动轨迹测试下得到的关节变量曲线连续且无剧烈跳动，说明任意当前解总是在前一个全局最优解周围搜索得到，进一步验证了PSO算法求逆解的可行性。在运动初期，主要依靠SCARA机械手大臂、小臂的关节夹角变化来实现末端执行器位姿的改变，即遵循移动关节少动，旋转关节多动的原则以减少能耗，当插值位置点超过SCARA机械手的工作空间时，则需与Y轴模组协调配合，使得末端到达目标位置。

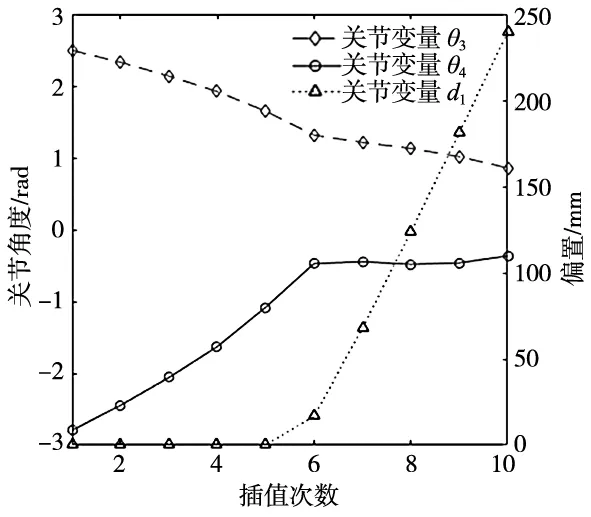
图6 连续运动轨迹测试所得逆解曲线图

4 结论

本文设计了一种混合型机械手，由Y、Z轴模组与SCARA机械手协调运动完成对晶圆片盒的传输。通过改进型D-H法推导出该机械手的运动学方程，并采取蒙特卡洛法对其工作空间进行分析；以位姿精度为约束条件、最小关节变化量为优化目标，结合PSO算法完成运动学逆解的求取。最后在MATLAB环境下仿真验证了逆解寻优方法正确有效，该机械手的工作空间可以满足工作使用要求，对传输机械手在半导体工艺设备中的开发应用具有一定参考价值。