格室加筋土等效强度计算方法对比研究

付 娆，宋 飞

（长安大学公路学院，陕西 西安 710064）

0 引 言

土工格室是一种三维立体网状或蜂窝状结构的土工合成材料，对填土具有较强的侧向限制作用。目前土工格室对加固软土地基、堤坝工程、河道治理、挡土墙及边坡防护等方面产生了良好的工程效果，已广泛应用于土木工程各个领域。

虽然土工格室在我国得到了广泛的应用，成功解决了大量工程问题，但是对土工格室加筋土结构的设计方法和设计规范仍不成熟，格室加筋土的强度仍无成熟计算方法。一些学者采用三轴试验和数值模拟方法对格室加筋土的力学性质进行研究，Bathurst和 Karpurapu[1]、Rajagopal等[2]、Madhavi Latha 和 Murthy[3]、Wu 和 Hong[4]、Chen 等[5]、陈建峰等[6]、宋飞等[7]采用三轴试验研究了土工格室加筋土及土工织物包裹砂砾料的刚度和强度力学性质。他们的研究结果均表明，环形土工合成材料的约束作用可以等效为填料的围压增量，由于约束围压的作用，填土的刚度和强度会有所增加，土工合成材料的侧限约束作用在填土中引起的黏聚力增量称之为表观黏聚力，但加筋土的内摩擦角和未加筋土基本相同。侯娟等[8]采用三维有限元数值分析方法研究了高强土工格室的作用机理，研究结果表明，高强土工格室中既有对土体侧壁的摩擦作用，又有格室内部砂土的环箍作用，可有效地限制砂土的水平位移，提高地基承载力。基于对土工格室加筋土三轴试验结果的分析，Bathurst和Karpurapu[1]、Rajagopal等[2]提出了基于填料内摩擦角的格室加筋土等效强度计算方法，得到了广泛应用。但是上述方法存在如下问题：计算过程中含有土工格室加筋土的破坏轴向应变这一未知数，这一参数必须通过土工格室加筋土的三轴试验确定，在实用过程中极不方便；计算中假定体变为 0，这一假设条件的误差以及对于不同相对密度填料的适用性仍需进一步研究；计算公式仅考虑了填土内摩擦角对表观黏聚力的影响，未考虑填料应力应变关系的非线性以及砂砾料内摩擦角随围压增加而减小的力学特性对于表观黏聚力的影响。

针对上述问题，宋飞等[9]采用增量法，基于弹塑性理论、土的屈服准则、剪胀方程以及薄壁圆筒张拉理论推导了基于填料应力-应变关系的土工格室加筋土等效强度计算方法，并且用土工格室加筋土的大型三轴试验结果、土工织物包裹碎石桩的常规三轴试验结果，验证了所提计算方法的正确性和有效性。该方法解决了基于填料内摩擦角的计算方法不能考虑填料体变以及无法确定土工格室加筋土的破坏轴向应变这两大问题，能够反映填料应力-应变关系的非线性、压硬性和剪胀性以及填料内摩擦角随围压变化这种强度非线性的力学特性对表观黏聚力的影响。

为了更加深入研究基于内摩擦角和基于应力应变关系两种方法在计算土工格室加筋土复合材料等效强度上的差别，本文在简要介绍两种计算方法公式的基础上，通过对比两种方法计算所得的表观黏聚力与填土邓肯-张模型非线性弹性常数以及土工格室刚度参数之间的关系，分析表观黏聚力变化规律，加深人们对土工格室加筋土力学特性及应力-应变响应计算方法的认识，为土工格室加筋土结构设计提供参考。

1 两种计算方法简介

1.1 基于填料内摩擦角的计算方法

根据 Bathurst等[1-2]提出的土工格室加筋土等效强度计算公式，格室的约束围压引起的表观黏聚力由式（1）确定，即：

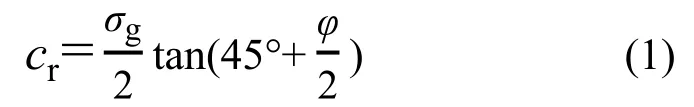
式中：φ为土的内摩擦角；σg为由于格室约束作用引起的围压增量，其表达式由式（2）得到[1-2]，即：

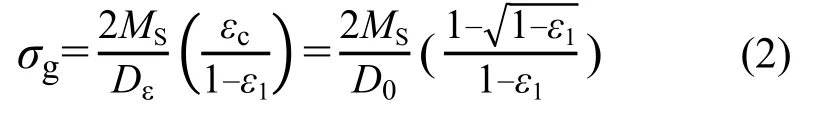
式中：ε1为试样的轴向应变；εc为试样在轴向应变ε1时的圆周向应变；MS为拉伸应变达到εc时对应的土工格室片的割线模量，由格室片的拉伸实验确定；D0，Dε为试样最初的直径和达到轴向应变ε1时的直径。

1.2 基于填料应力-应变关系的计算方法

根据宋飞等[9-10]提出的土工格室加筋土等效强度计算公式，土工格室内填料的竖向大主应力增量dσ1和水平小主应力增量dσ3之间的关系由式（3）确定，即：

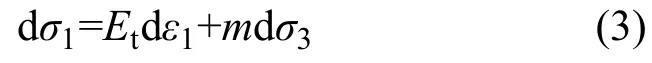
式中：Et为邓肯-张双曲线应力-应变关系中的切线模量，根据Duncan等[11]确定其表达式如下：

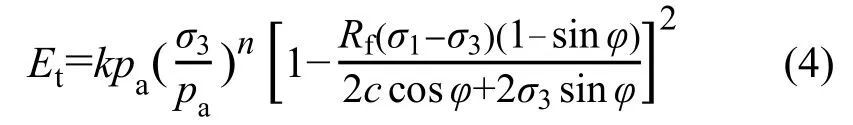
式中：k、n为试验常数；Rf为破坏比式；φ为材料内摩擦角；pa为大气压；取值为101.4 kPa。式（3）中m为表述竖向应力增量和水平方向增量之间关系的系数，由填料屈服函数确定，可由下式确定[9-10]：

式中：f为填土的屈服函数，一般条件下采用Mohr-Coulomb屈服函数、修正剑桥屈服函数、P-Z模型屈服函数来计算m，根据宋飞等[9]的研究结果表明，P-Z模型屈服函数总体确定m而言比其他两个屈服函数预测效果更好。p和q分别为填料的球应力和剪应力，在三轴应力状态下分别为：p=(σ1+2σ3)/3，q=σ1−σ3。

式（3）中dσ3=dσc+dσg，σc为土工格室加筋土的小主应力；σg为土工格室提供的约束围压。若忽略加筋土围压的变化，则有dσc=0。

dσg为格室引起的约束围压增量，其表达式为[9-10]：

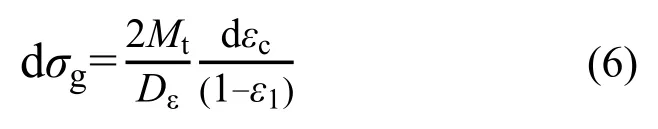
式中：Mt为格室的切线模量；Dε为试样达到轴向应变ε1时的直径，由式（7）确定[5]，即：

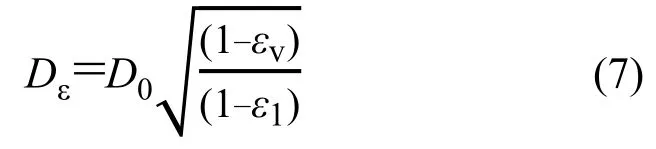
土工格室的圆周向应变εc可由下式得到[5]，即：

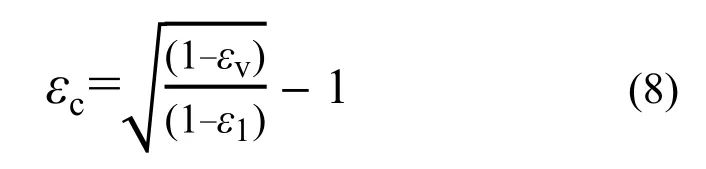
式（8）中填土的体应变εv由剪胀方程确定，对于砂砾料而言，常用的剪胀方程有 Rowe剪胀方程[12]，Pastor-Zienkiewicz模型中的剪胀方程[13]等。如采用P-Z剪胀方程，则侧向应变增量由下式确定：

体应变增量由下式确定：

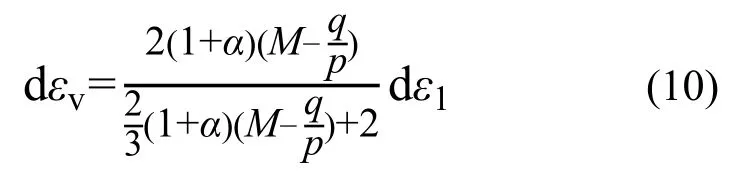
式中：α为材料常数，根据Pastor等[13-14]，Pastor[15]，Ling 和 Liu[16]，Cola[17]，Ling 和 Yang[18]，Miral[19]，Ravanbakhsh 和Hamidi[20]，Heidarzadeh 和 Oliaei[21]，对于干砂α一般可以取0.45。M可以由下式得到：

式中：φcr是指土的残余摩擦角。

如果假定格室加筋土的圆周向应变均匀，则其增量dεc由式（12）确定[9-10]，即：

根据式（3）～（12）递推迭代可求得土工格室加筋土的应力应变关系，根据Mohr-Coulomb准则以及格室拉力和结点强度比较来判别加筋土的破坏，详细的递推迭代过程详见宋飞等[9-10]的研究。将式（6）计算出的所有迭代步的dσg相加得到总的格室约束围压σg，将σg代入式（1）可得表观黏聚力cr。

采用该方法计算表观黏聚力时需要用到填土的邓肯-张模型的非线性弹性常数k、n、Rf、峰值内摩擦角φ和残余内摩擦角φcr。参数的确定方法详见Duncan 等[11]和 Boscardin 等[22]。

2 两种方法计算结果比对

经过试算后发现n对于计算结果影响较小，本文主要讨论k和Rf对格室加筋土表观黏聚力的影响，对比分析基于填料内摩擦角的方法和基于填料应力应变关系的方法的差别。计算中采用 Mohr-Coulomb屈服函数和P-Z剪胀方程。

2.1 参数k的影响分析

k由轴向应变和偏差应力的关系确定，采用邓肯-张双曲线模型进行计算，由下式确定：

式中：k和n分别代表斜率；Ei为土在邓肯-张双曲线应力-应变关系中的起始模量。根据常规三轴试验结果整理k和n的方法详见Duncan等[11]的研究。

图1给出了当格室加筋土的弹性常数Rf=0.9，φ=37°，φcr=32°，两种计算方法计算出的表观黏聚力cr随参数k的变化关系曲线。参考Madhavi Latha等[3,23]的研究结果，采用Bathurst公式计算表观黏聚力cr时，对于中密砂和密砂，破坏轴向应变可近似取为0.05。

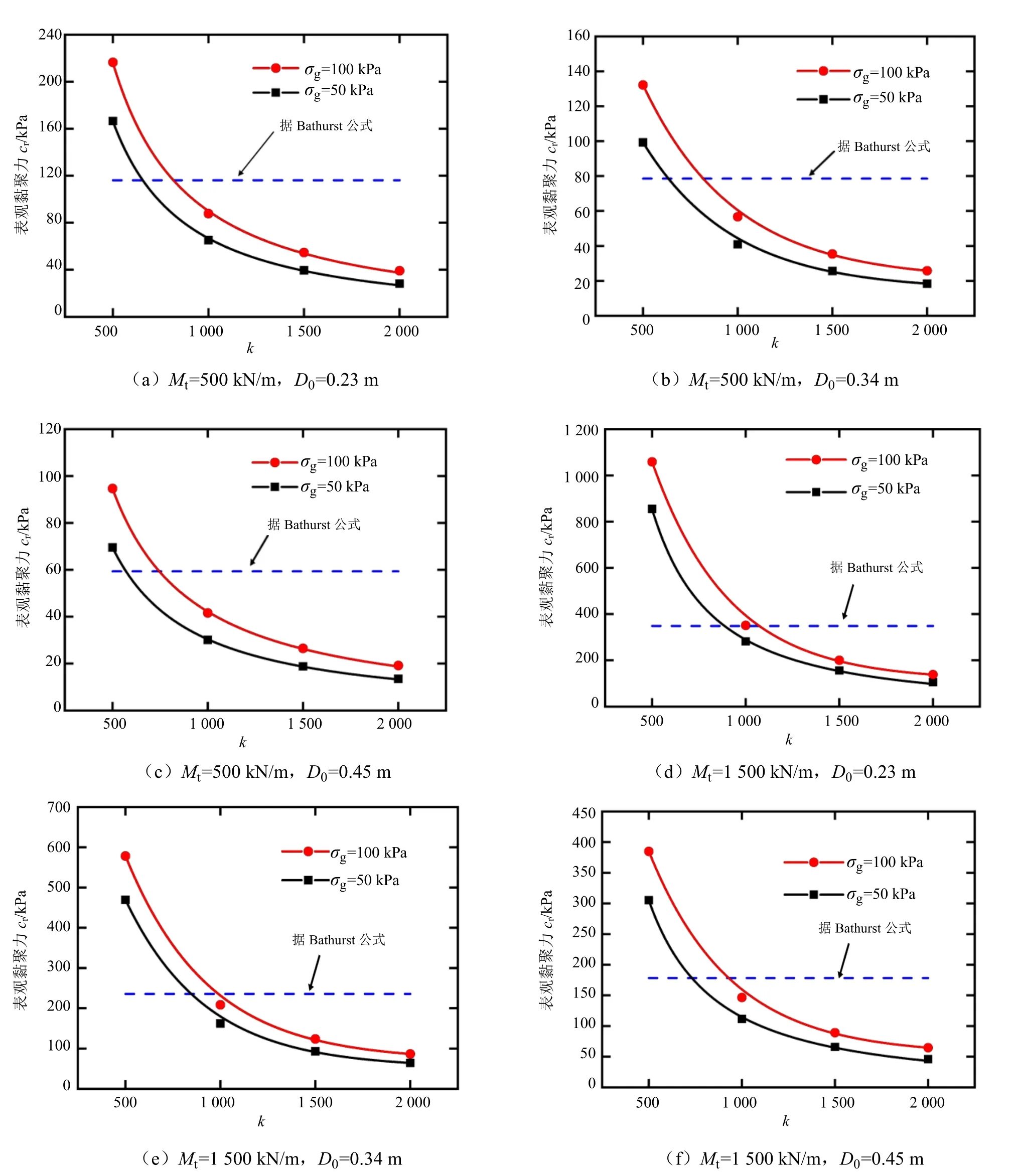
图1 参数k与表观黏聚力关系Fig.1 Relation between parameter k and apparent cohesive force

由图1的对比分析可以看出：

（1）当填土的内摩擦角φ确定后，用 Bathurst公式计算的表观黏聚力cr不随参数k变化，用基于填料应力应变关系的方法计算的表观黏聚力cr随参数k的增大而减小。这是由于在填料的应力应变关系中，两种方法达到的峰值一样，内摩擦角一样，但是二者达到峰值所需的破坏轴向应变不一样，应力应变关系的非线性不一致，由Bathurst公式可知，表观黏聚力cr仅与内摩擦角有关，所以表观黏聚力cr不随参数k变化；由基于填料应力-应变关系的计算公式可知，当k较小时，应力应变曲线达到峰值较晚，破坏轴向应变较大，导致在填土破坏之前格室约束围压发挥较大，因此得到的表观黏聚力也较大，所以k与cr成负相关；

（2）用两种方法计算出的表观黏聚力cr都与土工格室参数Mt正相关，与D0负相关；

（3）无论在哪种围压下，用基于填料应力应变关系的方法得出的曲线趋势和形状大致相同，k越小，改变土工格室参数Mt、D0对表观黏聚力cr的影与直线的截距和响越大。

2.2 参数Rf的影响分析

邓肯-张双曲线模型试验常数Rf代表试样的破坏比，其表达式如下：

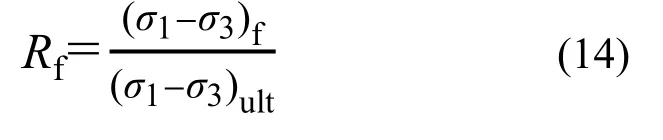
其中：(σ1−σ3)f为破坏偏差应力，(σ1−σ3)ult为极限偏差应力。

图2给出了当格室加筋土的试验参数k=1 500，φ=37°，φcr=32°，两种计算方法计算出的表观黏聚力cr随参数Rf的变化关系曲线。与前文参数k的影响分析一致，破坏轴向应变可近似取为0.05。

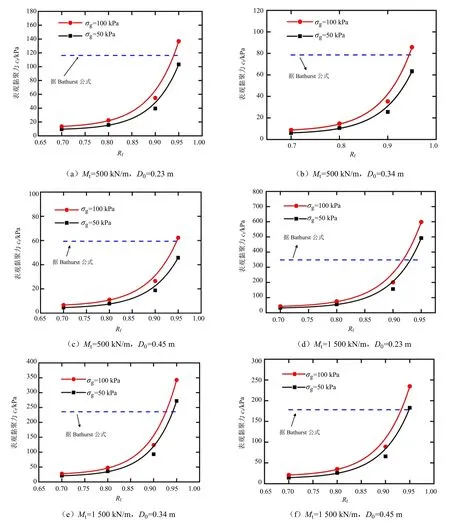
图2 参数Rf与表观黏聚力关系Fig.2 Relation between parameter Rf and apparent cohesive force

由图2的对比分析可以看出：

（1）当填土的内摩擦角φ确定后，用 Bathurst公式计算出的表观黏聚力cr不随参数Rf变化，用基于填料应力应变关系的方法计算的表观黏聚力cr随参数Rf的增大而增大。这是由于在填料的应力应变关系中，两种方法达到的峰值一样，内摩擦角一样，但是二者达到峰值所需的破坏轴向应变不一样，应力应变关系的非线性不一致，由Bathurst公式可知，表观黏聚力cr仅与内摩擦角有关，所以表观黏聚力cr不随参数Rf变化；由基于填料应力-应变关系的计算公式可知，当Rf较小时，应力应变曲线达到峰值较早，破坏轴向应变较小，得到的表观黏聚力也较小，所以Rf与cr成正相关。

（2）无论在哪种围压下，用基于填料应力应变关系的方法计算时，Rf越大，改变土工格室参数Mt、D0对表观黏聚力cr的影响越大。

3 结 论

本文通过对比基于填料内摩擦角以及基于填料应力应变关系计算土工格室复合材料等效强度方法，研究表观黏聚力与填土邓肯-张模型非线性弹性常数、土工格室刚度参数之间的关系，得到如下结论：

（1）对于砂砾料，当填土的内摩擦角φ确定后，用 Bathurst公式计算的表观黏聚力cr不随试验参数k、Rf变化，用基于填料应力应变关系的方法计算的表观黏聚力cr与参数k成负相关，与参数Rf成正相关。

（2）用两种方法计算出的表观黏聚力cr都与土工格室参数Mt正相关，与网格尺寸D0负相关。

（3）无论在哪种围压下，用基于填料应力应变关系的方法计算时，当k越小，Rf越大时，改变土工格室参数Mt、D0对表观黏聚力cr的影响越大。