基于桥桩保护的带撑双排桩基坑支护实例及有限元分析

熊一帆，刘广新，杜 威，应宏伟

（1.河海大学岩土工程科学研究所，江苏 南京 210098；2.浙江省铁投建设工程有限公司，浙江 温州 325000；3.杭州铁路设计院有限责任公司，浙江 杭州 310016；4.浙江大学滨海和城市岩土工程研究中心，浙江 杭州 310058；5.浙江工业大学土木工程学院，浙江 杭州 310023）

0 引 言

随着城市建设的快速发展，地上空间的开发和利用已渐渐不能满足人们的需求，大量的深基坑工程应运而生。近年来，基坑工程的施工规模和难度逐渐增大，周边环境也越来越复杂，这对变形的控制提出了更高的要求。Clough等[1]研究了采用锚杆和内支撑的基坑土方开挖引起的围护结构变形的3种形式；刘兴旺等[2]对15个基坑工程的监测数据进行了分析，得出了软土地区围护结构的最大侧向变形一般在0.002～0.009倍开挖深度。基坑施工过程中，不仅需要关注围护结构本身的变形，也需要关注基坑卸荷导致的周边环境的变形。上世纪90年代初期，Finno等[3]首先提出观点：深基坑的施工中，土方开挖卸荷易引起相邻建（构）筑物桩基的较大位移，从而对建（构）筑物产生不利影响。Poulos等[4]、Chen 等[5]、杜金龙等[6]、木林隆等[7]利用离心机试验及数值分析等方法对此问题进行了更深入的研究，得到了一些重要的结论。当基坑邻近既有桥梁桩基对变形控制要求较高时，双排桩门架式结构常被作为支护结构，并设置水平内支撑，研究双排桩支护结构的具体参数对邻近桩基的影响具有十分重要的工程意义。

本文以某下穿市域铁路桥梁的市政道路箱涵基坑工程为研究对象，介绍了双排桩结合两道内支撑和坑内地基土加固的支护方案，对实测数据进行了分析，并采用有限元软件建立了数值模型，分析研究了有无支撑、支撑间距及排桩间距等因素对围护结构及桥桩变形的影响。

1 工程概况

1.1 基坑与轨道交通的相对关系

某城市新建道路下穿市域铁路立交工程，采用四孔分离式框架箱涵，该基坑南北方向长40.7 m，东西方向宽36 m，其平面如图1所示。基坑与已运营的市域铁路桥梁斜交，夹角为 88˚。基坑围护结构外侧与北承台结构净距为3 m，距桥墩8.6 m；与南承台结构净距仅为1.9 m，距桥墩7.5 m。

图1 基坑平面示意图Fig.1 Plane diagram of foundation pit

1.2 基坑支护方案

基坑剖面如图2所示，开挖深度8.6 m，辅道箱涵底标高−1.575 m，辅道箱身高度7.45 m，主道箱涵底标高−3.308 m，主车道箱身高度7.25 m。基坑围护结构采用直径1.0 m、桩间距1.2 m的双排门架式钻孔灌注桩加两道内支撑和两道换撑形式，桩长32～36 m。第一道内支撑梁采用1.2×1.2 m钢筋混凝土梁支撑，第二道内支撑及两道换撑均采用Φ609×16 mm钢管支撑，支撑水平间距4.0～6.0 m。受场地限制，双排桩的排距为2.5 m，小于3～5d（d为围护桩直径）的常规排距，属小排距双排桩。

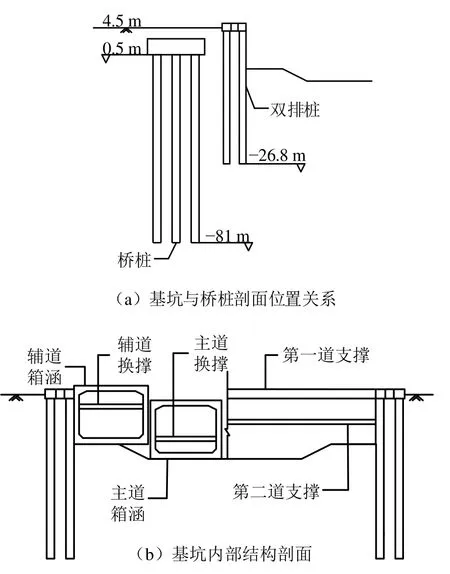
图2 基坑剖面示意图Fig.2 Section of foundation pit

1.3 土层条件

表1给出了包括加固土在内的土层力学参数，开挖影响深度范围内为深厚淤泥，呈流塑，厚层状，偶含贝壳碎屑、粉砂薄层及有机质，土质不均，局部为淤泥质黏土或淤泥质粉质黏土，有光泽，干强度高，韧性高，该层力学性质极差，渗透性能弱。因缺少相关资料，将全风化基岩等效为上层粉质黏土层进行建模。地下水埋藏较浅，渗透性能弱，接受大气降水与地下径流补给，以蒸发或向低洼处径流为排泄方式，受季节气候变化影响较大，稳定水位埋深0.30～3.50 m。

表1 土层力学参数Table 1 Soil mechanical parameters

1.4 施工工况

基坑的施工分为11个阶段，具体工况见表2。

表2 施工工况Table 2 Construction conditions

2 二维数值分析

2.1 计算模型

为了研究基坑开挖对邻近桥桩的影响，本文以图2为基础构建了二维有限元模型。为了减小边界效应对最终计算结果的影响，本文模型水平宽度取90 m，竖向边界则取至粉质黏土层底部。

HSS土体本构模型能够合理模拟土体小应变下的刚度和土体非线性、硬化等特性，因此本文选取HSS本构模型进行计算，部分模型参数采用王卫东等[8]的建议，具体数值见表3。

表3 部分HSS模型参数Table 3 Partial HSS model parameters

HSS土体本构模型的强度参数为有效应力指标，具体取值如表1所示。土体的刚度系数关系则由王卫东等[8]的建议及工程经验得到。土体刚度参数取值见表4，围护桩、桥桩等结构参数见表5。

表4 HSS模型的刚度参数Table 4 Stiffness parameters of HSS model kN/m2

表5 结构参数Table 5 Structural parameters

模型的网格划分精度为中等，共生成3 711个单元、31 291个节点，网格划分如图3所示，施工步则按照实际工况模拟。

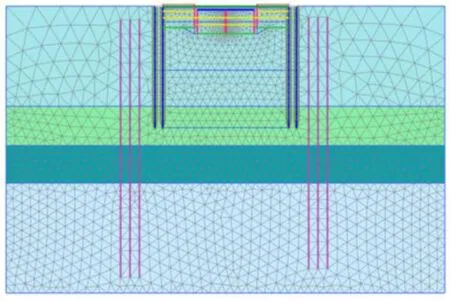
图3 网格划分Fig.3 Mesh subdivision

2.2 结果分析

实际工程中基坑测斜管、桥桩沉降以及坑外土体沉降监测点如图3所示。工况11中后排桩和桥桩的监测数据、有限元结果及其对比见图4和表6，图 4中位移为正代表排桩向坑内变形（下同）。值得说明的是，所有数据均取自工况 11拆除辅道换撑，此时箱涵及回填混凝土已有一定的强度，形成了完整的支护体系，这对于变形控制极为关键。从后排桩水平位移的实测曲线可以看出，围护桩最大位移24.2 mm，最大变形出现在坑底以上2.6 m，小于预警值35 mm，说明基坑处于安全状态。至于桥桩变形，表6中桥桩沉降的监测值为2.2 mm，小于预警值4 mm，说明桥桩处于安全状态。经过对比，有限元计算得到的围护结构侧向位移曲线形状与实测侧向位移曲线基本吻合，桥桩沉降值与实测值吻合，验证了数值模型和计算参数的合理性，为下文的研究奠定了坚实的基础。

图4 排桩水平位移对比Fig.4 Comparison of row piles horizontal displacement

表6 桥桩沉降对比Table 6 Comparison of bridge pile settlement

地表沉降也是基坑施工时需要关注的重点，由于地表沉降监测剖面与数值模型选取的剖面并不一致，因此不将二者进行比较而只分析实测数据。地表沉降的监测数据如图5所示。拆除辅道换撑时，坑外最大沉降出现在了距离后排桩约4.5 m处，数值为 22.53 mm，说明基坑施工对周边环境影响不大。

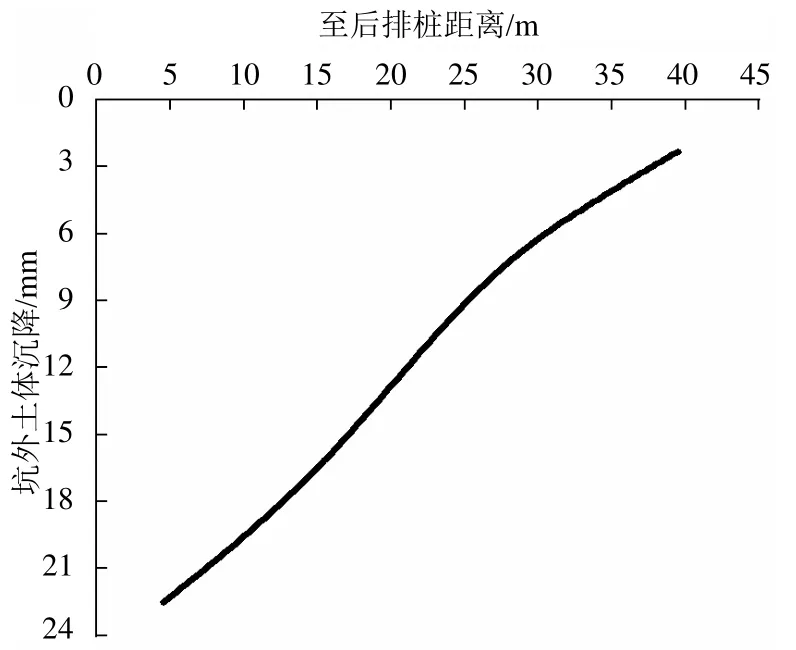
图5 地表沉降实测结果Fig.5 Measured results of surface subsidence

3 影响因素分析

以上述模型作为参考算例，进一步研究有无支撑、支撑间距以及排桩间距对围护结构及桩基变形的影响。

3.1 算例1（有无支撑的影响）

不激活参考算例中的第一道和第二道支撑作为算例1来计算。算例1与参考算例的后排桩水平位移比较见图6，桩基沉降对比见表7。由图6和表7可知，悬臂式支护结构使后排桩水平位移及墙后桩基沉降明显增大，不利于基坑整体变形的控制。因此，在设计中合理地布置内支撑可以明显改善基坑支护的效果。

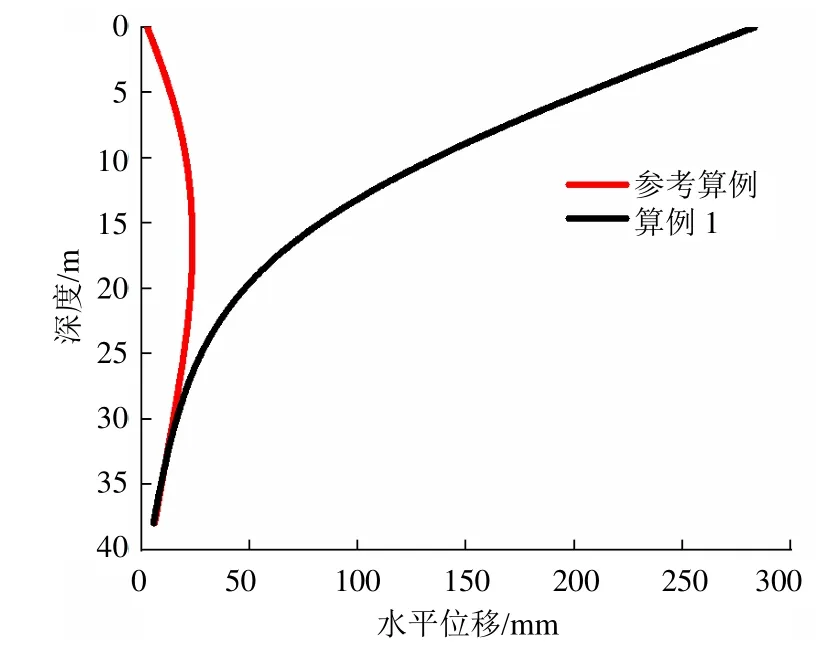
图6 有无支撑对排桩水平位移的影响Fig.6 Influence of support on horizontal displacement of row piles

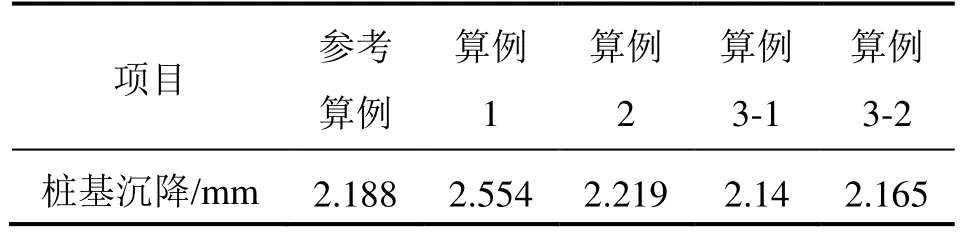
表7 不同算例的沉降对比Table 7 Settlement comparison of different examples

3.2 算例2（支撑间距的影响）

将参考算例中的支撑及临时换撑的间距从5.06 m增大到10.12 m作为算例2。算例2与参考算例的后排桩水平位移比较见图 7，桩基沉降对比见表7。由图7和表7可知，相对参考算例，算例2的后排桩水平位移和桩基沉降增大，增大支撑间距起到了与减小支撑刚度同样的作用，即降低了带撑双排桩支护结构的整体刚度，对变形控制不利[9]。但在支撑间距成倍增加的情况下，变形变化量并不大。

图7 支撑间距对排桩水平位移的影响Fig.7 Influence of support spacing on horizontal displacement of row piles

3.3 算例3（排距的影响）

基坑常规设计中，双排桩排距可取2～5d。将参考算例中的排距从2.5d增大到3.75d和5d作为算例3-1和3-2。算例3-1和3-2与参考算例的后排桩水平位移比较见图 8，桩基沉降对比见表 7。由图8和表7可知，相对参考算例，算例3-1和3-2的后排桩水平位移以及桩基沉降减小，增大排距即增大双排桩支护结构的整体刚度[10]，可以有效地降低带撑双排桩支护结构的水平位移和邻近桩基的沉降。然而，在整体刚度增大的情况下，算例 3-1中的桩基沉降反而要小于算例 3-2，这是因为改变排距会改变后排桩到桩基的距离，使两个算例中的桩基处在了沉降三角影响区的不同位置，进而导致最终沉降的差异。

图8 排距对排桩水平位移的影响Fig.8 Influence of row spacing on horizontal displacement of row piles

4 结 论

（1）结合某下穿既有市域铁路的箱涵基坑工程，分别对后排桩水平位移、桥桩沉降以及地表沉降进行分析。实测结果表明，后排桩水平位移、桥桩沉降以及地表沉降都小于预警值，证明该工程变形控制得较好，小排距带撑双排桩支护结构的支护效果较为明显。

（2）对监测数据和有限元结果进行对比，验证了该模型的合理性。改变支护结构参数并进行分析，发现排桩间距越大，带撑双排桩整体刚度就越大，对于围护结构变形的控制效果就越好，但改变排距的同时会改变排桩与桩基的间距，进而影响最终沉降量的大小，所以一味地增大排距并不一定能保证邻近桩基沉降的减小。