基于斜坡响应的实用闭环系统辨识方法及其应用

杨栋，曹子飞，潘凤萍，吴茂坤，吴振龙

(1.华电莱州发电有限公司，山东 烟台 261441；2.南方电网电力科技股份有限公司，广东 广州 510080；3.郑州大学 电气工程学院，河南 郑州 450001)

随着越来越多的风电、太阳能和潮汐等新能源并入电网，火电机组面临着越来越大的运行压力[1-2]：①在保证机组安全的情况下，需要加快机组的负荷响应速率以吸纳更多的新能源并入电网；②机组在运行过程中需要保证较强的抗干扰能力；③为保证火电机组参与深度调峰过程中的控制品质，系统必须具有很好的鲁棒性。建立能够很好反映系统动态的模型并优化控制器的参数，是解决上述压力的有效手段。

然而在实际中面临着2个难题：①由于火电机组在运行过程中一般不允许进行开环扰动试验，如何基于闭环系统的扰动试验数据得到能够很好反映系统动态的高精度模型是一个需要解决的问题；②如何对现场应用的控制器参数进行进一步的整定与优化，提高系统的控制性能与鲁棒性是另一个值得关注的问题。通过闭环扰动试验建立的模型能够为控制器参数的优化提供模型基础，如PID控制器[3]和自抗扰控制器(active disturbance rejection controller，ADRC)[4]，然而在工程实际应用时，闭环辨识方法的研究仍有许多工作需要完成。PID控制器的参数优化往往是在不断的试验与调整中完成的，这需要大量的试验与工程经验，不利于参数优化方法的大规模推广应用[5]。基于建立的较高精度的模型，从平衡控制性能与鲁棒性的角度出发，结合工程实际，给出PID控制器参数整定方法是十分必要的。

闭环系统辨识的研究方法很多并取得丰富的理论成果[6]。文献[7]针对柔性传动系统，详细比较了直接闭环辨识方法和间接闭环辨识方法的优缺点，并通过实验验证了理论分析结果。文献[8]采用递推扩展最小二乘法对电液伺服系统的位置、加速度、力闭环系统完成自适应辨识，并通过实际电液伺服系统验证了所提方法的有效性。文献[9]针对非最小相位系统从频域角度出发，通过获取被控对象在重要频率范围内的频率响应特性，采用最小二乘法从幅频与相频两部分得到被控对象的闭环传递函数。文献[10]讨论了多输入多输出系统的数据信息属性和可辨识性，能够将被控对象辨识为离散系统。文献[11]通过分析辅助变量的子空间方法在闭环条件下可能产生偏差的原因，给出了消除偏差的解决办法，从而将对象辨识为离散系统。文献[12]提出了一种正交分解的辅助变量子空间辨识方法，旨在提高辨识的精度。文献[13]研究了含有定常扰动、状态估计存在误差时的一类二阶非线性系统的闭环参数辨识算法，通过最小二乘法和状态估计器对系统参数和常扰动进行线性化估计，得到被控对象参数。文献[14]从时域角度给出了包含控制器参数的闭环系统的最小二乘形式，并通过递推最小二乘法辨识被控对象的未知参数。文献[7-13]将被控对象辨识为离散系统，然而由于离散系统受采样周期影响明显，采样周期的不合理会带来病态的运算基础，这也很难在得到的模型中被发现，会造成控制策略优化改进和先进控制方法实施的失败。文献[14]可以得到阶跃响应下的闭环系统的连续传递函数，然而不能忽略火电机组中的前馈作用，闭环系统的辨识需要考虑前馈控制的影响。此外，阶跃信号激励由于信号的突然变化容易对执行器带来不可逆的伤害，所以在实际中很难被允许应用，比如火电机组中的负荷变化，一般是通过斜坡信号响应实现而不是阶跃信号响应。基于斜坡信号激励的闭环辨识能够实现化工、能源领域中系统的辨识，为后续被控对象的动态特性分析、控制器设计优化提供基础，具有很好的工业应用潜力。

PID控制器、PI控制器在火电机组中应用广泛[15]，参数整定方法多达上千种。文献[16]梳理了工业过程中稳定对象、不稳定对象、积分对象的PID控制器、PI控制器参数整定方法。文献[17]基于预期动态方程，提出了带有串联滤波器的PID控制器形式，给出基于性能指标和鲁棒性指标最优值的参数整定方法，并进行了仿真验证。文献[18]推导了二阶不稳定时滞系统通过PID控制器所能达到的时滞裕度的下界，并为控制器参数整定提供指导。此外，利用相对时滞裕度法整定PID控制器也得到很多关注[19]，该方法能够在保证鲁棒性的前提下提高闭环系统的控制性能。通过启发式优化算法对控制器参数优化也是常见的方法[20]，如遗传算法、粒子群优化算法和模拟退火等多种优化算法。Skogestad内模控制(Skogestad internal model control，SIMC)法通过研究一阶惯性加纯延迟(first order plus time delay，FOPTD)和二阶惯性加纯延迟(second order plus time delay，SOPTD)系统的零极点配置的特点，总结出对象的经验公式[21]。实际系统控制器的优化需要在保证系统鲁棒性的前提下进行，即在保证系统具有很强的应对系统不确定性的前提下，尽可能提升系统控制性能。

基于工程实际需求，为提高机组的运行品质，本文提出一种基于斜坡响应并考虑前馈控制的闭环系统辨识方法，推导出时域连续系统的最小二乘形式，并通过仿真与现场数据验证该方法的可靠性与有效性。基于辨识的模型，提出考虑鲁棒性约束的PI控制器参数整定方法，在保证鲁棒性约束的前提下提升系统的跟踪性能与抗干扰性能。

1 基于斜坡响应的闭环辨识方法

本文研究如图1所示包含有前馈控制器和反馈控制器的闭环系统，其中r和y分别为系统的参考信号和系统输出。图1中反馈控制器C(s)的数学表达式为

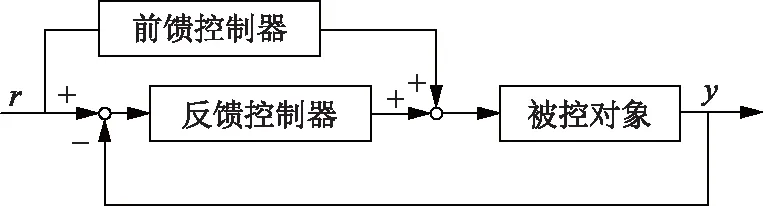
图1 包含前馈控制器和反馈控制器的闭环系统

(1)

式中：kp、ki、kd分别为反馈控制器C(s)的比例增益系数、积分增益系数、微分增益系数；s为微分算子。

前馈控制器为Cf(s)的数学表达式为

(2)

式中：kpf、kif、kdf分别为前馈控制器Cf(s)的比例增益系数、积分增益系数、微分增益系数。

被控对象采用SOPTD系统进行描述，数学表达式为

(3)

式中：G(s)为SOPTD系统的传递函数；K为被控对象的增益；T1、T2为时间常数；τ为延迟常数。当T1≠0时，式(3)等价为

(4)

式中k=K/T1、a1=T2/T1和a2=1/T1为待辨识参数。需要说明的是,延迟常数τ可以通过设定值与系统输出响应之间的时间偏差直接得到。因此，在本文中所提的方法中,延迟常数τ被认为是已知或者提前估计已知的。

考虑到火电机组中大部分回路是单回路系统，从参考信号到系统输出的传递函数

(5)

结合式(1)、(2)可以得到

(6)

式(6)可以转化为时域最小二乘形式，即

y(t)+a1y[1](t)+a2y[2](t)+kkdy[1](t-τ)+

kkpy2(t-τ)+kkiy[3](t-τ)=

k(kdf+kd)r[1](t-τ)+k(kp+kpf)

r[2](t-τ)+k(kif+ki)r[3](t-τ).

(7)

其中，

式中：t为时间；ρ、p、q均为积分量y和r的中间积分时间量。

实际运行的数据采用离散采样的方式进行采集，闭环系统斜坡响应的幅值为l，斜率为γ，不超过τ/ΔT(ΔT为系统的采样周期)的最大整数为m，不超过(τ+l/γ)/ΔT的最大整数为ξ，可以得到：

r[1](t-τ)=

(8)

r[2](t-τ)=

(9)

r[3](t-τ)=

(10)

(11)

(12)

(13)

(14)

(15)

式(8)—(15)中i表示第i个数据。

通过代数转换，式(7)等价以下最小二乘形式：

y(t)=ψT(t)θ.

(16)

其中：

θ=[a1a2k]T，

ψT(t)=

kpy2(t-τ)+kiy[3](t-τ)-

(kdf+kd)r[1](t-τ)-(kp+kpf)r[2](t-τ)-

式(16)为包含前馈和反馈控制的闭环系统的最小二乘形式，批处理最小二乘法(batch least square，BLS)、递推最小二乘法(recursive least square，RLS)和辅助变量最小二乘法(auxiliary variable least square，AVLS)均可用于获得θ=[a1a2k]T的估计值。

如果采用BLS方法，θ=[a1a2k]T的估计值

(17)

其中，

ψ=[ψ(1)ψ(2) …ψ(N)]T，

z=[y(1)y(2) …y(N)]T，

式中N为数据采样的总长度。

如果采用RLS方法，θ=[a1a2k]T的估计值

(18)

其中，

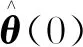
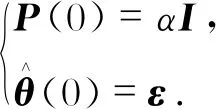
(19)

其中α可以选择一个足够大的正实数(104～1010)，ε可以取零向量或者足够小的正向量。

如采用AVLS方法，θ=[a1a2k]T的估计值

(20)

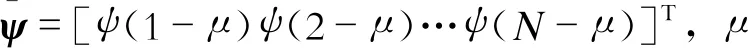
此时，基于闭环系统的参考信号和系统输出数据以及前馈和反馈控制器参数，可以得到待辨识对象的参数θ=[a1a2k]T。综合考虑实施的难易程度和计算量大小，本文中应用RLS方法。

需要说明的是采用实际微分形式的PID形式为

(21)

式中M为滤波系数，此时可以得到参考信号到系统输出的传递函数

(22)

基于前面介绍的分析方法，可以得到采用实际微分形式的PID控制器的闭环辨识结果。

2 仿真验证与现场应用

针对第1章的理论分析结果进行仿真验证，并将该方法应用于某电厂4号低压加热器，采用本文提出的方法将低压加热器的模型辨识出来，为后续的控制器优化提供基础。

2.1 仿真验证

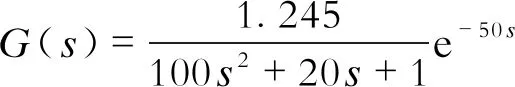
工况1：标称工况下延迟常数精确已知。此时延迟常数的估计值与真实值无偏差，即τ=50 s，闭环辨识模型参数为k=0.010 59、a1=0.171 6、a2=0.008 511，此时辨识模型与系统输出如图2所示。可以看出辨识模型能够很好地吻合实际系统的输出，说明本文所提方法具有很高的辨识精度。

图2 标称工况下延迟常数精确已知时的闭环辨识结果

工况2：延迟常数未精确已知。此时延迟常数的估计值与真实值有一定偏差，即τ=40 s和τ=55 s，此时闭环辨识模型参数分别为k=0.056 9、a1=0.865 3、a2=0.045 74(τ=40 s时)和k=0.001 1、a1=0.337 9、a2=0.000 889 4(τ=55 s时)，此时2个辨识模型与系统输出如图3所示。可以看出尽管延迟常数与真实值存在一定偏差，辨识的模型仍然能够很好地吻合实际系统的输出，说明本文所提辨识方法对于延迟常数具有较强的鲁棒性，能够保证在延迟常数有偏差时仍具有较高的辨识精度。

图3 延迟常数未精确已知时的闭环辨识结果

工况3：前馈控制存在一定偏差。由于实际系统的前馈控制逻辑是复杂的控制逻辑，理论计算的前馈控制与实际的前馈控制有一定的偏差，这里用kpf的一个静态偏差来表征，可以得到如图4所示的结果，kpf=0.05时的辨识结果为k=0.015 19、a1=0.202 7、a2=0.011 73，kpf=0.15时的辨识结果为k=0.005 867、a1=0.111 4、a2=0.004 88。由图4可知，kpf的偏差会来带一定的控制效果偏差，辨识模型输出仍能够较好吻合实际系统的输出，说明本文所提辨识方法对于前馈控制具有较强的鲁棒性，能够保证前馈控制存在偏差时仍具有较高的辨识精度。

图4 前馈控制不精确时的闭环辨识结果

图5 三阶系统的闭环辨识结果

2.2 算法鲁棒性讨论

为进一步分析本文所提算法的鲁棒性，本节分2种情况进行讨论，即系统输出存在不同随机白噪声以及实际系统存在不确定性和不同随机白噪声的工况，在其他参数保持不变的情况下，进行300次蒙特卡洛实验。表1和表2分别给出上述2种工况下的相关统计指标。从表1可知当系统输出存在不同的随机白噪声时，辨识的相关模型参数的数学期望很接近真实值，说明算法具有很强的鲁棒性，策略噪声对于模型的辨识精度影响较小。从表2可知，实际系统存在±10%的不确定性和不同随机白噪声时，模型参数的平均相对偏差均在±5%以内，特别是K和T2的平均相对偏差在±0.5%以内，说明所提算法的鲁棒性较强，能够比较好地应对实际系统的不确定性和测量噪声，具有满足工业实际应用的潜力。

表1 测量噪声存在不确定性时蒙特卡洛实验统计结果

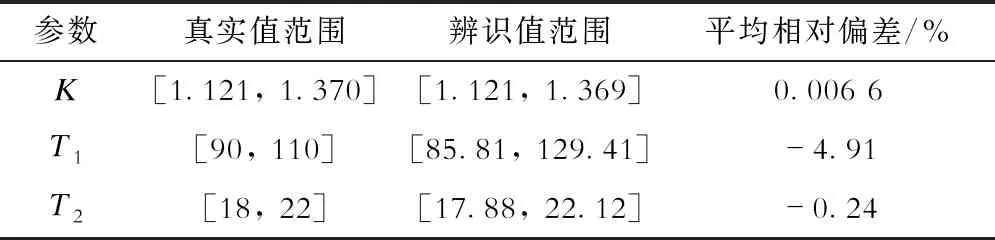
表2 被控对象存在不确定性时蒙特卡洛实验统计结果

2.3 现场应用

(23)

实际运行数据与辨识模型的输出对比如图6所示，可知辨识模型能够很好地吻合系统输出实际值，说明辨识模型具有较高的准确度，能够应用于控制器参数的优化以及控制策略的设计。

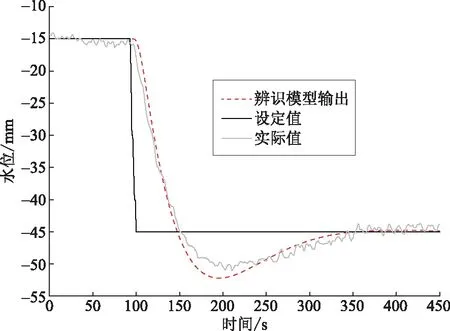
图6 低压加热器的闭环辨识结果

3 PI控制器参数优化和现场应用

3.1 基于鲁棒性约束的PI控制器参数整定

该低压加热器采用PI控制器，本文提出基于鲁棒性约束的PI控制器参数整定方法。鲁棒性指标采用最大灵敏度函数指标Ms[22]，其数学定义为

(24)

式中C(iω)、G(iω)分别为C(s)、G(s)的频域响应，ω为频率。Ms的物理含义为临界点(-1, 0)到S(iω)的Nyquist曲线最短距离的倒数，其合理范围为1.2≤Ms≤2.0，Ms值越小表示鲁棒性越强。

低压加热器在运行过程中的抗干扰性能也不应忽略，因此本文提出的基于鲁棒性约束的PI控制器参数整定方法为：

(25)

其中Isp和Iid分别为设定值跟踪性能与抗干扰性能的误差绝对值积分(integrated absolute error, IAE)的值。本文中鲁棒性约束指标选择为Ms≤1.3，选择优化指标为Isp和Iid之和。采用MATLAB自带的遗传算法(genetic algorithm，GA)函数进行优化，种群数为100，迭代次数为40，其他参数选择为默认参数，通过优化可以得到PI控制器的参数kp=-0.54、ki=-0.008 3。基于辨识的模型，原始PI控制器(kp=-0.4、ki=-1/180)与本文PI控制器(kp=-0.54、ki=-0.008 3)的控制效果如图7所示，其中设定值在10 s时进行幅值为1的阶跃，在300 s时添加幅值为1的输入扰动。由图1可知本文提出的基于鲁棒性约束的PI控制器较原始PI控制器具有更快的跟踪性能和更强的抗干扰性能，能够很好地抑制策略噪声。

图7 基于辨识模型的控制效果

为进一步定量分析上述PI控制器在应对模型不确定性时的能力，本文采用蒙特卡洛实验进行分析，辨识模型的参数k、a1和a2均存在±10%的不确定性，蒙特卡洛实验中k、a1和a2在辨识值的±10%范围内随机摄动，得到随机摄动的不确性模型，采用原始PI控制器和本文PI控制器对随机摄动的不确性模型进行控制，重复实验300次，得到Isp和Iid的分布如图8所示。Isp和Iid的分布越集中意味着鲁棒性越强，Isp和Iid越小表示控制效果越好。从图8可知，本文PI控制器比原始PI控制器的鲁棒性更强，控制效果更好，具有很好的工业应用潜力。

图8 Isp和Iid的分布

3.2 现场验证

基于前述理论分析与仿真验证，将原来的PI控制器参数(kp=-0. 4、ki=-1/180)在分散控制系统中替换为优化后的控制器参数(kp=-0.54、ki=-0.008 3)，分别进行设定值阶跃试验，得到如图9所示的跟踪性能结果，从图中可知原始PI控制器与优化PI控制器的超调量分别为50.43%和27.60%，优化PI控制器的控制效果能够有效降低设定值阶跃时的超调量。此外，二者的调节时间相当，这意味着优化后的PI控制器能够在不增加调节时间的前提下，有效降低水位变化时的超调量，对于低压加热器的安全运行具有重要的意义。

图9 跟踪性能对比

图10为低压加热器稳态运行的结果，时长8 000 s。可以看出优化后的PI控制器能够有效提高系统的抗干扰性能，能够将水位波动控制在更小的范围内，相关统计指标见表3。虽然优化PI控制器平均偏差比原始PI控制器的平均偏差大，但是波动范围与偏差的标准差分别只有原来的38.6%和14.8%，说明优化PI控制器提升了低压加热器稳态运行的扰动抑制能力，有利于低压加热器安全运行。

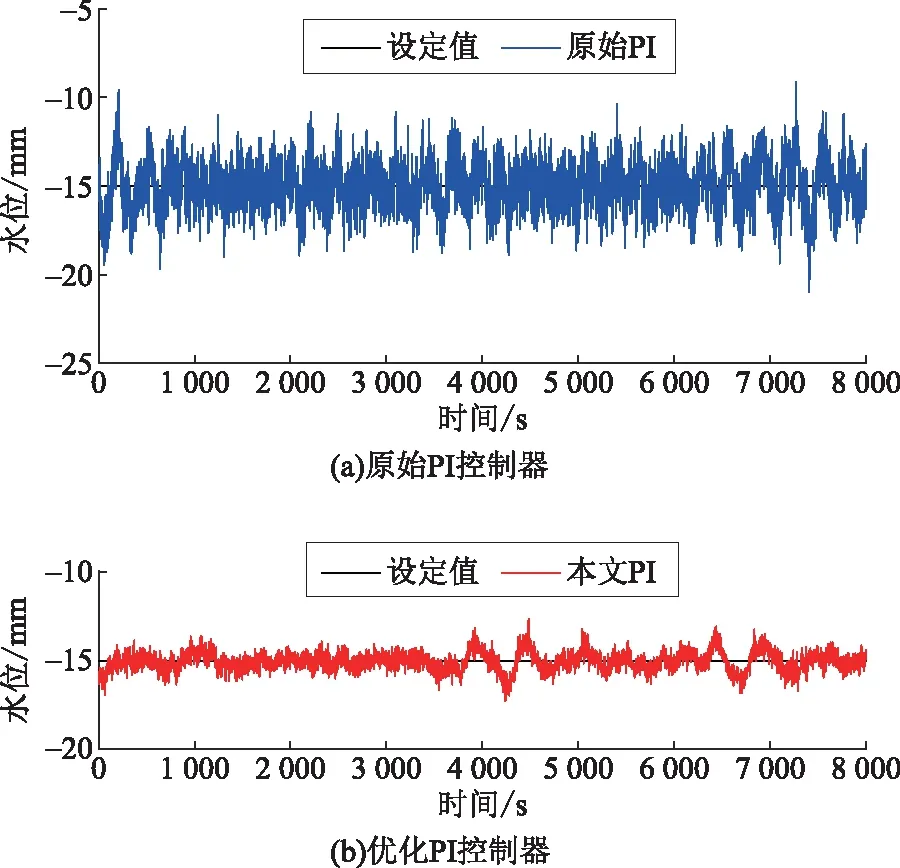
图10 抗干扰性能对比

表3 稳态运行的统计指标

4 结束语

火电机组在运行过程中，开环试验往往是不被允许的。为进一步对控制器参数进行优化，提升系统运行中的控制品质，本文提出了基于设定值斜坡响应的闭环辨识方法。本文的创新点如下：

a)推导基于斜坡响应并考虑前馈控制的闭环系统的时域连续系统最小二乘形式，通过现场数据验证所提方法的有效性。

b)提出基于鲁棒性约束的PI控制器参数整定方法，现场运行数据说明了基于辨识模型及优化参数在跟踪性能与抗干扰性能方面的优势。

本文所提出的闭环系统辨识方法能够进一步推广应用到其他系统，并服务于控制器的参数优化，对进一步提升火电机组的运行品质具有重要意义。