一种适应新型电力系统深度调峰快速调频的工程最速控制器
李军,黄卫剑,陈锦攀,王朋,周永言,朱亚清,潘凤萍,李德波
(1. 广东电网有限责任公司电力科学研究院,广东 广州 510080;2. 南方电网电力科技股份有限公司,广东 广州 510080)
电力工业[1]是涉及到各个产业的基础能源提供者,是关系国计民生和国家战略的基础支柱产业。电力系统[2]是由发电侧、电网侧(输电和配电)、用电侧等共同构成的庞大且具有很高复杂性的系统。发电侧是燃煤火力发电[2]、燃气发电[3-4]、水力发电[5]、核能发电[6]、风力发电[7]、太阳能光伏发电[8]等多种电源共存的复杂系统。
随着环境保护的迫切需要以及“双碳”任务的提出,以风力发电、太阳能光伏发电为代表的新型绿色能源在我国得到迅猛发展,对减少大气碳排放量具有积极意义,这也是新型电力系统的基本特点。为了适应新型电力系统中绿色能源装机容量的快速增长,电网亟需快速增加调峰、调频能力。在我国发电侧结构中,目前火电机组在电网总装机容量中占比达到52%,通过对现有火电机组控制系统优化(即大幅提升深度调峰和快速调频性能)来增加电网调峰、调频容量,是一种投资省、见效快的方式,是目前阶段电网快速增加调峰、调频能力的主要方式。
建立市场机制是推进电网快速增加调峰、调频容量的有效途径,2018年以来,电网调频辅助服务市场[9-10]的建立和完善,在发电系统引发了新一轮过程控制技术改进的需求,要求提高现有火电机组[11-12]负荷响应速度和精度,更要求确保火电机组运行的安全性,保证重要过程参数平稳和不超标。但现有火电机组过程控制普遍采用的比例-积分-微分(proportional-integral-differential,PID)控制[13-15]加前馈控制[16-17],难以继续满足这种要求,这对电力企业的研究人员提出了很大的技术性挑战,催生出满足此种需要的新型控制技术。
2018年,广东电网的研究团队发明出一种区别于PID控制的新型基础控制器(new foundation controller,NFC)[18],其代表了一种工程最速控制器(engineering fastest controller,EFC),适应现有火电机组大幅提升深度调峰和快速调频服务能力的客观需要。以EFC为核心开发出的火电机组辅助调频外挂控制系统,在广东省主力火电机组得到快速普及,仅在2020年1月—2021年6月期间,就已经应用于38台火电机组(总计容量25 600 MW)辅助调频外挂控制系统的商业合同项目。
1 控制科学的发展和火电机组过程控制技术的基本现状
火电机组的热工控制系统简称为“热控系统”,热控系统普遍采用分散控制系统(distributed control system,DCS)[19]。现场总线控制系统[20]被认为是热控系统的发展方向,但是并没有得到普及。近年来,出现了DCS结合外挂系统的复合形式,例如DCS加外挂可编程序控制器[21]等。
应该说,火电厂过程控制技术与控制科学[22]的发展息息相关,控制理论的发展为火电机组过程控制技术的选择提供了多种的可能性。
1788年,吉姆斯·瓦特借助离心调速器[22]实现了蒸汽机转速控制,对18世纪以蒸汽机为代表的第一次工业革命起到了巨大的推动作用。离心调速器代表的是一种比例作用的反馈控制,即瓦特原理[23]。离心调速器实现了初步的反馈控制,代表了在工业过程控制领域的第一代基础控制技术,离心调速器的明显问题是存在系统的稳态误差。
从19世纪末到20世纪上半叶,电机工程的发展开启了第二次工业革命,对控制提出了较高的要求,要求实现无系统稳态误差的精准控制。考仑德和斯蒂文森在1936年发明出PID控制器,有效提高了反馈控制性能,代表了在工业过程控制领域的第二代基础控制技术;在20世纪40年代,形成了以奈奎斯特建立的“奈奎斯特判据”[24]、伯德建立的反馈控制系统频域分析工具(即伯德图)[25]、伊文斯提出的根轨迹法[26]等为基础的经典控制论,适应了PID控制发展的需要。
为了适应航天航空领域的发展对控制理论的要求,在20世纪50年代末,形成了以庞特里亚金(前苏联)提出的极大值原理[27]、贝尔曼创立的动态规划[28]和卡尔曼建立的卡尔曼滤波理论[29]等为基础的现代控制论[30]。经过半个多世纪,由此产生出宏大和严密的现代控制论,发展出众多的先进控制策略[31-33]。
在控制理论和技术的发展过程中,还产生出种类丰富的、介于经典控制与先进控制之间的一类高性能控制策略,例如内模控制器(internal model controller,IMC)[34]、Smith预估控制器[35]、二阶内反馈控制器(second order of internal feedback controller,SO-IFC)[36]、新型高性能控制器(new high performance controller,NHPC)[37]等。
然而,控制理论和技术的发展丝毫没有撼动PID控制技术在工业过程控制领域的主导地位。至今为止,基于PID的反馈控制依然是包括火电机组过程控制在内的工业过程控制领域的一种首选基础控制技术。文献[30]指出:“当最优控制在航空航天领域取得辉煌成功的同时,它在工业控制上的影响却几乎为零”。文献[38]指出:“实际上,在工业过程中面对复杂多变的生产过程对控制系统的各种要求除了PID算法尚被基本认可外,其他的算法都很难长期、有效地得到应用”。
先进控制的实质是数学问题,其基础是数学模型[22],其解决的问题是求取数学上的最优性能指标[39]。而火电机组的过程控制属于工程实际问题,区别于数学问题,例如准确的数学模型难以获取,解决的问题是求取保证过程参数不超标(如负荷、主蒸汽压力、主蒸汽温度、再热蒸汽温度的偏差满足火力发电厂相关规程的要求)的直观性能指标。数学上的最优性能指标与工程上的直观性能指标之间不一定是必然关系,如最优性能指标不代表能够满足直观性能指标的要求。钱学森等[40]指出:“只要比较直观的讲法能够达到目的,我们就不用严密的精巧的数学方法来讨论”。能够满足工程上的直观性能指标要求或者能够提高工业过程控制性能的范式,是符合事物发展规律的范式。
在火电机组过程控制领域,至今为止,PID控制、前馈控制依然是被大量运用的基础控制技术,它们占据着主导地位,这就是目前火电机组过程控制技术的基本现状,反映出控制理论研究与控制实际存在差距。
2 工程最速控制器
2018年,PID的一种本质缺陷被揭示,这就是常规积分(conventional integrator,CI)作用存在跟踪常值扰动效率不高的本质缺陷[17-18]。长期以来,人们主要的研究方向是控制结构的问题(如IMC、Smith预估控制器、SO-IFC、NHPC等),鲜有人研究控制机制的问题,CI作用效率不高的问题就属于一种控制机制上的问题。
目前已经开发出2种EFC,一种是工程最速比例-积分控制器(engineering fastest proportional-integral,EFPI)与工程最速超前观测器(engineering fastest leading observer,EFLO)的串级结构,另一种是EFPI与工程最速比例-微分控制器(engineering fastest proportional-differential,EFPD)的串级结构,文中采用前者。EFC的基础是一种惯性组合滤波器(inertial combination filter,ICF)[41],ICF是一种滑动窗滤波器(sliding window filter,SWF)[17]的工程化。SWF代表了一种零加速度最速跟踪滤波器(fastest tracking filter,FTF),ICF代表了一种工程最速跟踪滤波器(engineering fastest tracking filter,EFTF)。所谓最速跟踪,即最快的跟踪输入或者跟踪输入的时间最小。相对PID控制器,EFC在控制机制上取得本质突破。
2.1 工程最速跟踪滤波器
首先需要了解FTF和一阶惯性滤波器(first order inertia filter,FOIF),表达式为
(1)
式中:fFTF(s)、TW分别为FTF的传递函数、窗口时间长度;fFOIF(s)、TFOIF分别为FOIF的传递函数、惯性时间常数;s为拉普拉斯算子。
文中变量包括符号的表达具有唯一性,出于表述简洁性的需要,对使用到的变量单位进行统一,如文中无特别说明,时间单位符号为s,增益量纲为一,阶次量纲为一,相位单位符号为°。
现有一些系统(如DCS)实现FTF存在累计误差的问题,因此需要对FTF进行工程化。工程化结果得到
(2)
式中:fEFTF(s)为EFTF的传递函数;n为整数阶次。
在n=16、TW=TFOIF=100 s、输入单位阶跃信号时,得到FTF、EFTF、FOIF输出特性的仿真实验结果,如图1所示,图中PFTF(t)、PEFTF(t)、PFOIF(t)分别为FTF、EFTF、FOIF在单位阶跃输入的过程输出,t为时间。

图1 滤波器输出特性
很明显,FTF、EFTF输出跟踪输入的速度远高于FOIF,EFTF较好地实现了FTF的工程化。文中如无特别说明,默认EFTF的n=16。
EFTF有多种重要用途,如用于过程信号滤波,构造工程最速积分器(engineering fastest integrator,EFI)、工程最速微分器(engineering fastest differentiator,EFD)、EFPI、EFPD、EFLO等。
2.2 工程最速比例-积分控制器与工程最速比例-微分控制器
首先需要了解构造CI的特殊方法,将FOIF作用于一种正反馈环节,得到的CI如图2所示。

图2 常规积分器示意图
CI表达式为

(3)
式中fCI(s)、TI分别为CI的传递函数、积分时间常数,在数值上TI=TFOIF。
同样的原理,用EFTF构造EFI,如图3所示。

图3 工程最速积分器示意图
EFI表达式为
(4)
式中:fEFT(s)、TEFI分别为EFT的传递函数、积分时间常数,在数值上TEFT=TW。在n=16,s趋于∞或s趋于0时,fEFT(s)分别简化为
(5)
根据式(5),在TEFT=TI,将EFI与CI进行对比可知:当s趋于∞,则EFI与CI相同;当s趋于0,则EFI的增益是CI的1.882倍。这是EFI积分作用效率显著高于CI的数学依据。
在TI=TEFT=100 s,输入单位阶跃信号,得到CI、EFI输出的仿真实验结果,如图4所示,图中PCI(t)、PEFI(t)分别为CI、EFI在单位阶跃输入的过程输出。显然,EFI的积分作用效率显著高于CI。

图4 积分器输出特性
EFPI表达式为
fEFPI(s)=KEFPI(1+fEFI(s)),
(6)
式中fEFPI(s)、KEFPI分别为EFPI的传递函数、外部比例增益。
EFPD表达式为
(7)
式中:fEFPD(s)为EFPD的传递函数;fEFD(s)、TEFD分别为EFD的传递函数、微分时间常数,在数值上TEFD=TW。
2.3 工程最速超前观测器
EFLO表达式为
(8)
式中:fEFLO(s)、TEFLO分别为EFLO的传递函数、超前观测时间常数,在数值上TEFLO=TW;KC为变换增益,原则上KC≫1,文中固定KC=10;fFOF(s)、TFOF分别为一阶滤波器(first order filter,FOF)的传递函数、滤波时间常数。设置TFOF的基本原则是EFC的噪声功率增益(noise power gain,NPG)[18]不大于10,属于一种较低的噪声干扰水平。
在TEFLO=263 s,TFOF=5.66 s,得到EFLO频率特性的数学计算结果,如图5所示,图中ω为角频率,HEFLO(ω)、GEFLO(ω)分别为EFLO的相位特性、增益特性,HEFLO,P=87.86°为HEFLO(ω)的峰值,表明EFLO具有较高的超前相位。
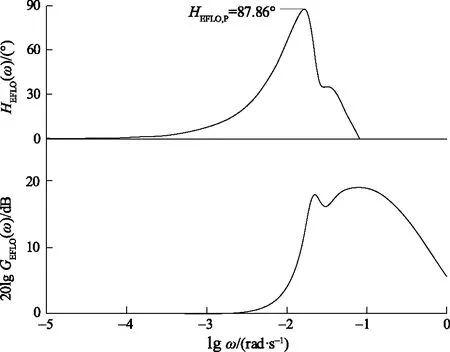
图5 EFLO频率特性
2.4 工程最速控制器参数整定
将Z-N法则[42]用于EFC参数整定,Z-N法则代表了一种工程建模方法,简称ZNM模型(Ziegler-Nichols model,ZNM)[18],表达式为
(9)
式中fZNM(s)、KZN、τZN、TZN分别为ZNM的传递函数、增益、纯滞后时间常数、时间常数。
EFC参数整定原则为
(10)
式中TCA为常数调整项,0≤TCA≤TZN/2。
2.5 工程最速控制系统
具体的EFC控制系统如图6所示,图中,被控过程采用黑箱过程(black box process,BBP),仅能够通过在BBP输入施加单位阶跃获取BBP的输出过程信息,然后根据过程信息建立BBP的ZNM。文中将BBP设置为难控制过程,为的是增加研究的难度。外扰采用斜坡函数(ramp function,RF),其中RF速率为10-3s-1,RF长度为1 800 s。BBP、外扰耦合模型(external disturbance coupling model,EDCM)为
(11)
式中:fBBP(s)、fEDCM(s)分别为BBP、EDCM的传递函数。
建立BBP的ZNM,如图7所示,图中PBBP(t)、PZNM(t)分别为BBP、ZNM在单位阶跃输入的过程输出。

图7 ZNM过程输出特性
根据图7,得到KZN=1、τZN=226 s、TZN=276 s,进一步得到
(12)
2.6 最优PI、PID控制
衡量EFC控制性能需要有对比对象,文中将EFC与最优PI(optimal proportional-integral,OPI)、最优PID(optimal proportional-integral-derivative,OPID)进行对比。
PI、PID控制系统如图8所示,图中C表示PI、PID控制器。

图8 PI、PID控制系统示意图
文中的PID为二阶滤波PID、二阶惯性逆模型(second order inertia inverse model,SOIIM)、CI、二阶惯性滤波器(second order inertia filter,SOIF)的串级结构。PI、PID为
(13)
式中:fPI(s)、KP分别为PI的传递函数、比例增益;fPID(s)为PID的传递函数;TSOIIM为SOIIM的时间常数;TSOIF为SOIF的时间常数。
在PID中,将TSOIF固定为0.054TSOIIM的目的是保证PID的NPG在10以内。
文献[14]提出了基于开环系统相位裕度(phase margin,PM)和幅值裕度(amplitude margin,AM)的OPID参数整定方法,文中将PM作为优化手段,将获取PI、PID的最小积分值作为优化目标,得到OPI、OPID参数,同时将过程振荡衰减率不小于75%作为OPI、OPID参数是否有效的判定准则。
用MPI,ZNM表达PI控制ZNM的PM,MPID,ZNM表达PID控制ZNM的PM。以搜索OPI参数为例,在给出的PM条件下,通过连续改变KP和TI,得到TI随KP变化的关系曲线,在TI随KP变化的最小点,得到OPI参数。同样的原理,得到OPID参数。其中在MPI,ZNM=MPID,ZNM=60°,得到的搜索结果如图9所示。

图9 最优控制参数搜索结果
图9中,在关系曲线上标出的黑点对应OPI、OPID参数,代表积分值最小即抑制常值扰动性能最高。具体得到OPI参数为KP=0.69、TI=366 s,OPID参数为TSOIIM=145 s、TI=296 s。
用OPI、OPID控制BBP,得到的仿真实验结果如下节的图11、图12所示,OPI、OPID控制的主要性能指标见表1、表2。根据过程振荡衰减率不小于75%的判定准则,判定OPI、OPID参数有效。
2.7 工程最速控制器性能
根据式(12)给出的ZNM,得到TCA的调整范围在0~138 s,设置TCA=125 s,得到EFC参数为KEFPI=1、TEFI=377 s、TEFLO=263 s,在TFOF=5.66 s,得到NPG为10。
为了保证闭环控制具有良好的稳定性能,文献[30]建议控制系统的PM在45°左右。出于研究的需要,给出EFC控制BBP的PM和AM随TCA变化关系的数学计算结果,如图10所示,图中AEFC,BBP、MEFC,BBP分别为EFC控制BBP的AM、PM。其中:在AEFC,BBP=3 dB,得到TCA=128 s;在TCA=138 s,得到MEFC,BBP=48.5°。这表明了在TCA调整的上限,EFC能够保证较高的稳定性能。

图10 相位裕度、幅值裕度与常数调整项的关系
将EFC、OPI、OPID进行对比,在过程给定为1时,得到的仿真实验结果,如图11所示,图中POPI(t)、POPID(t)、PEFC(t)分别为OPI控制BBP、OPID控制BBP、EFC控制BBP的过程输出,得到EFC、OPI、OPID控制的主要性能指标,见表1。
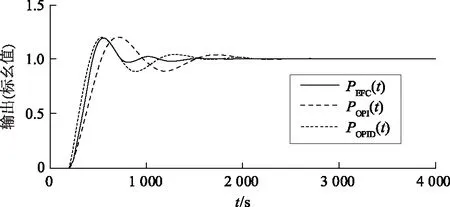
图11 EFC、OPI、OPID控制特性对比结果

表1 EFC、OPI、OPID控制的主要性能指标
调节时间是指过程进入到小于5%偏差的时间,相对OPI、OPID,EFC显著提高了调节性能。
在过程给定为0,外扰为RF,得到的对比结果如图12所示。

图12 EFC、OPI、OPID外扰抑制特性对比结果
根据图12,得到EFC、OPI、OPID外扰抑制的主要性能指标,见表2。

表2 EFC、OPI、OPID外扰抑制的主要性能指标
用抑制RF最大偏差衡量EFC外扰抑制性能,相对OPI、OPID,EFC外扰抑制性能分别提高了78.6%、43.7%。很显然,EFC外扰抑制性能显著优于OPI、OPID。
3 工程最速控制器的商业应用
本章给出EFC的3个典型商业应用案例,其中前2个应用案例是PID控制难以胜任的。
3.1 应用案例1
火电机组锅炉再热蒸汽温度的控制设计有减温喷水控制和烟气挡板控制2种方式:减温喷水控制的主要优点是容易采用自动控制,缺点是经济性较差,减温喷水每增加锅炉额定负荷的1%,锅炉的效率将降低0.2%;烟气挡板控制的主要优点是经济性较好,但是难以采用自动控制,被热工界认为是一个世界性难题。
在2019年4月—5月期间,采用EFC对某电厂4号600 MW超临界火电机组再热蒸汽温度的烟气挡板控制系统进行优化。具体设计了烟气挡板与减温喷水的协同控制方式,当再热蒸汽温度高出设定值8 ℃以上时加入减温喷水控制,其中烟气挡板控制部分的优化如图13所示。

图13 烟气挡板控制优化示意图
图14是2019-04-26T13:00—14:00,4号机组在负荷指令560 MW→430 MW→510 MW变负荷过程中,烟气挡板控制采用EFC优化后的控制特性趋势图。

图14 优化后烟气挡板控制特性
图14中,再热蒸汽温度设定值为600 ℃,再热蒸汽温度最大波动为+6.8 ℃/-5.3 ℃,因未高出设定值8 ℃以上,减温喷水控制部分未动作。
3.2 应用案例2
将EFC运用于提高现有火电机组综合调频性能,首先需要了解综合调频性能规则,文献[10]公布的综合调频性能指标规测为
K=0.5K1+0.25K2+0.25K3
(14)
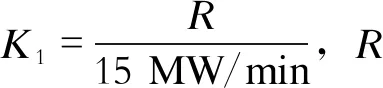
K值越高,代表综合调频性能指标也越高。对于火电机组,要提高K值,只能通过缩短锅炉风、煤、水变化响应时间,加大锅炉风、煤、水变化幅度,提高机组变负荷速率等实现;然而风、煤、水的快速变化,机组变负荷速率的提高,必然会引锅炉主蒸汽压力、锅炉主蒸汽温度、锅炉再热蒸汽温度等重要过程参数的大幅波动,甚至可能危及机组运行安全。因此,提高K值不是一个简单的技术问题,需要综合考虑各种因素,在提高K值的同时,又要将重要的过程参数控制在允许的区域。
在2019年5月—7月期间,为提高机组综合调频性能,以EFC为核心采用外挂系统方式,对某电厂3号1 000 MW超超临界火电机组的锅炉主控、汽轮机主控、中间点蒸汽温度、一级过热蒸汽温度、二级过热蒸汽温度、再热蒸汽温度烟气挡板、再热蒸汽减温喷水实施控制优化。图15是2019-09-19T08:00—12:00,3号机组在负荷设定速率为20 MW/min、负荷指令590 MW→820 MW→410 MW变负荷过程中,重要过程参数的控制特性趋势图。

1—目标负荷;2—负荷设定;3—实际负荷;4—锅炉主蒸汽压力设定;5—锅炉主蒸汽压力;6—锅炉主蒸汽温度;7—锅炉再热蒸汽温度。
在图15给出的趋势范围,锅炉主蒸汽压力最大偏差0.63 MPa/-0.59 MPa,锅炉主蒸汽温度最大偏差6.5 ℃/-5.9 ℃,锅炉再热蒸汽温度最大偏差7.3 ℃/-6.7 ℃,负荷与设定值偏差小于5 MW。EFC对重要过程参数的控制性能良好,满足火力发电厂相关规程的要求。
表3是3号机组于2019-09-18T12:00—17:00的综合调频性能指标K值,平均值为1.15;而在优化前,3号机组K值只有0.5~0.6。可见,经优化后,机组综合调频性能有了大幅提升。

表3 连续6 h综合调频性能指标
由此可知,采用EFC提高现有火电机组的辅助调频性能是行之有效的方法。
3.3 应用案例3
2021年1月期间,将EFC应用于某电厂3号600 MW超临界火电机组的一级过热蒸汽温度控制回路,并且与PID控制进行对比,得到的对比结果如图16所示。

1—一级过热蒸汽温度设定;2—一级过热蒸汽温度;3—实际负荷;4—一级过热蒸汽减温器喷水指令。
图16中,首先投入PID控制,在10:45切换到EFC。在给出的趋势范围,投入PID期间,相对一级过热蒸汽温度设定值,一级过热蒸汽温度最大偏差为5.9 ℃/-8.2 ℃;在切换到EFC后,一级过热蒸汽温度最大偏差为5.1 ℃/-3.3 ℃。总体看,EFC显著优于PID。
4 结束语
在工程实践中,研究人员揭示出PID存在CI作用跟踪常值扰动效率不高的本质缺陷,由此促进了EFC的发明,显著提高了反馈控制性能,且没有复杂繁琐的数学解析过程,显著区别于现有的控制理论研究。在某种意义上,EFC是瓦特原理的继续深入发展,代表了在工业过程控制领域暨离心调速器、PID控制之后的第三代基础控制技术,从现阶段看,EFC代表了今后一个时期火电机组过程控制技术的一种发展方向。
以提高火电机组辅助调频性能为目标的商业应用已经证明,EFC是一种成熟的技术,相对PID控制,其稳定性能更好,性能和效率更高,参数整定更加容易,能够更好地适应难控制过程。可以预见,EFC对工业过程控制技术的实质性进步将产生良好的促进和推动作用。
EFC的快速发展有效释放了新型绿色能源,对未来碳达峰、碳中和具有积极意义。

