基于探地雷达的特厚煤层厚度动态探测技术

刘万里，马修泽，张学亮

(1.中国矿业大学 机电工程学院，江苏 徐州 221116; 2.北京天地玛珂电液控制系统有限公司，北京 100013)

智能化开采是煤炭综合机械化发展的新阶段，是我国煤炭工业发展的必由之路[1-2]。构建精确的煤层三维模型，是实现智能化开采的关键技术之一[3-5]。目前煤层初始模型的构建主要基于钻孔、三维地震、槽波CT和巷道三维扫描等数据。受制于源数据数量、源数据处理、插值方法选择等各种因素的影响[6]，导致利用这些数据构建的初始煤层三维模型不精准，垂向分辨率较低，误差一般大于煤层厚度的10%。为了提高煤层三维模型局部建模精度，迫切需要提供更多高精度的巷道煤厚信息来对初始煤层三维模型进行局部修正，以减小插值带来的误差[7]。

目前，井下常用的煤厚测量方法有以下3种:井下钻孔探测、透射槽波探测、探地雷达探测。① 井下钻孔探测虽然具有很高的探测精度，但是探测效率较低，并且钻孔与钻孔之间距离较大，内插出的煤层厚度具有一定误差[8]。② 透射槽波探测是利用槽波的频散特性(即槽波传播的速度随频率的变化而发生改变)来进行探测的，当频率一定时，槽波波速随煤厚增加而减小，选择对煤厚分辨率最高的频率进行层析成像，再根据巷道处已知钻孔煤厚和工作面揭露的煤厚拟合出群速度-煤厚关系式，就可以根据群速度层析成像法获取煤厚测量信息[9-10]。因此，透射槽波探测煤厚的缺点也很明显，即当煤厚变化较大时，选取的层析成像频率相对于煤厚分辨率开始下降，槽波探测的误差就会偏大。③ 探地雷达是利用电磁波在不同介质中传播时分界面会形成强反射信号的原理，可实现对煤岩界面进行探测，进而计算出煤厚[11]。利用探地雷达探测煤厚具有便携、高效、实时等优点，是目前煤厚探测最有效的手段之一。

为了实现基于探地雷达的煤厚信息精准探测，国内许多学者对此开展了大量的研究。其中，具有代表性的有:李亮等[12]使用400 MHz的雷达天线对煤厚1～3 m的煤岩分界面进行静态探测，并使用动态探测来加强图像的解释，但并未给出探测精度。刘帅等[13]使用超宽带探地雷达进行了薄煤层煤厚静态测量，通过局部的动态测量来加强对数据的解释，测量结果表明煤厚探测误差小于10 mm。张守祥等[14]使用频段为5.3～8.8 GHz的脉冲雷达对薄煤层的煤岩分界面进行静态探测，测量精度达到了20 mm。上述研究虽然在探地雷达探测煤厚方面取得了一定的成果，但还存在以下问题:

(1)上述研究的探测对象主要偏向于薄煤层，目前对特厚煤层(即厚度大于8 m的煤层)探测尚未开展相关研究。相较于薄煤层，特厚煤层具有煤厚变化幅度大、夹矸层数多、夹矸厚度变化不均匀、对雷达信号衰减严重等特点，严重的阻碍了特厚煤层厚度的精确测量。

(2)在实际煤层中，通常会存在一些夹矸层，夹矸与煤的介电常数是不同的，但是在计算时通常把夹矸看作煤层的一部分来进行计算，因此在计算时所使用的介电常数实际为“等效介电常数”，而实际煤层的介电常数会随着夹矸厚度变化而变化，这会给煤厚测量造成较大的测量误差。

(3)上述研究煤厚探测方式主要以静态探测为主，有时会辅助一些动态探测图像来加强对数据的解释。这种探测方式只能测出某一个点的煤厚信息，然后逐点测量，不仅效率很低，而且2个测点之间的煤厚只能通过插值的方法得到，精确度不高。

为此，笔者在详细分析了上述研究不足以及特厚煤层探测误差产生原因的基础上，提出基于探地雷达的特厚煤层厚度动态探测技术，其不但具有很高的效率，而且还可以获得较高的探测精度。主要思路如下:首先利用带通滤波、增益调节等处理方式实现煤岩分界面的准确识别;其次对钻孔处煤层进行静态点测，并对钻孔处煤层的介电常数进行精确校正，利用插值法获取相邻2钻孔之间的煤层介电常数;然后对煤层进行动态探测，通过移动定位技术实现动态测量数据精确定位;最后利用插值法获取的煤层介电常数与带有位置信息的探测数据计算出煤厚。最终实现特厚煤层厚度的动态测量，为煤层三维模型的局部修正提供基础数据。

1 雷达探测煤厚原理及误差分析

由于电磁波在传播过程中遇到不同介质时会产生波的反射与折射现象，所以当探地雷达发射的电磁波在空气、煤和岩石3种不同的介质中传播时，会在空气-煤分界面和煤-岩分界面产生能量较强的反射信号，2个界面的反射信号分别被接收天线接收，通过分析各个反射信号的电磁波传播时间即可确定各个分界面的位置，进而计算出煤层的厚度[15-18]。探地雷达测量煤厚原理如图1所示。

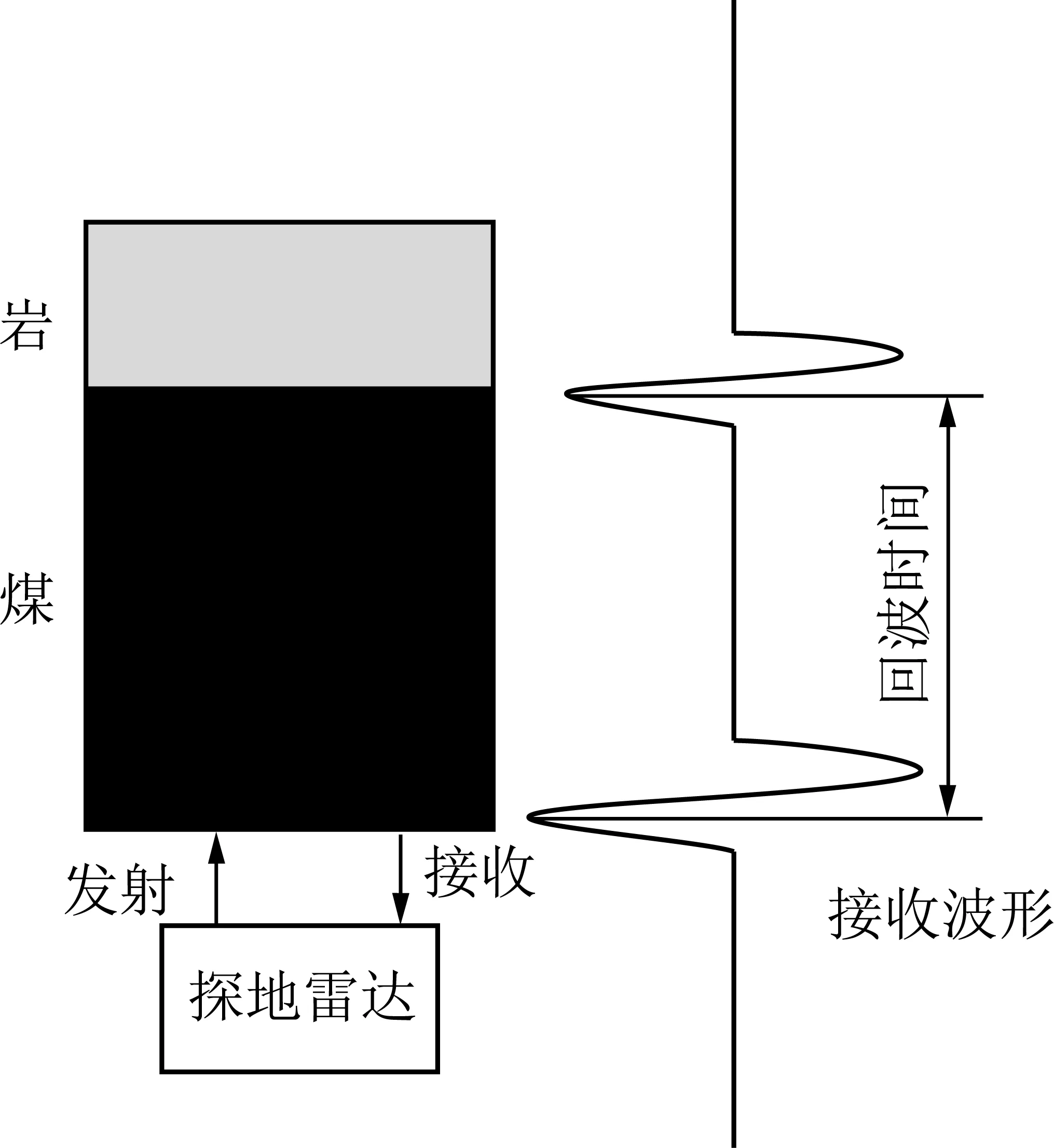
图1 探地雷达测煤厚原理Fig.1 Schematic diagram of the ground penetrating radar for measuring coal thickness

根据文献[14]，雷达在煤层中的传播速度v可表示为

(1)

式中，c为电磁波在真空中的传播速度,取0.3 m/ns;εr为煤层相对介电常数;μr为煤层相对磁导率;σ1为煤层电导率;ω为角频率。

由于煤的相对磁导率为1，当σ1/ω≪1时，式(1)可简化为

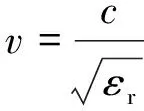
(2)

假设电磁波垂直射入，则所测煤厚d与电磁波在煤层中传播的回波时间t和电磁波在煤层中的传播速度v有关，煤厚d与回波时间t之间的关系可表示为

(3)

在使用探地雷达探测煤厚时，探测误差产生的主要原因可以归纳为以下5个方面:① 在测量时使用静态测量，测点与测点之间使用插值的方法计算煤厚时会带来一定的误差。② 在计算煤厚时，使用单一介电常数对煤厚进行计算时会产生一定的误差。③ 在探测过程中，测量数据无法与探测位置相对应将导致探测存在位置误差。④ 井下机电设备(采煤机、带式输送机等)发出的噪声和一些无线通讯系统(井下有线电话、输电线路、变频器等)产生的电磁辐射会对雷达电磁波的发射与接收造成干扰，导致煤岩界面回波信号被淹没或者回波信号不明显。⑤ 巷道顶部存在的铁丝网、锚杆等金属部件也会使电磁波信号有一定程度的衰减，使煤岩分界面变模糊，进而影响煤厚信息的判断。

综上可知，在进行特厚煤层厚度探测时应考虑不同探测区域煤层介电常数的差异、煤岩界面的准确识别以及如何实现动态探测。为此，笔者将在带通滤波等数据处理手段的基础上，研究利用介电常数精确校正技术与探测数据精确定位技术来实现特厚煤层厚度的动态连续测量，为煤层三维模型的局部修正提供基础数据。

2 特厚煤层厚度动态探测技术框架

为实现特厚煤层厚度的动态探测，在以上详细分析雷达探测煤厚原理及特厚煤层探测误差产生原因的基础上，提出基于探地雷达的特厚煤层厚度动态探测技术，其总体框架如图2所示。

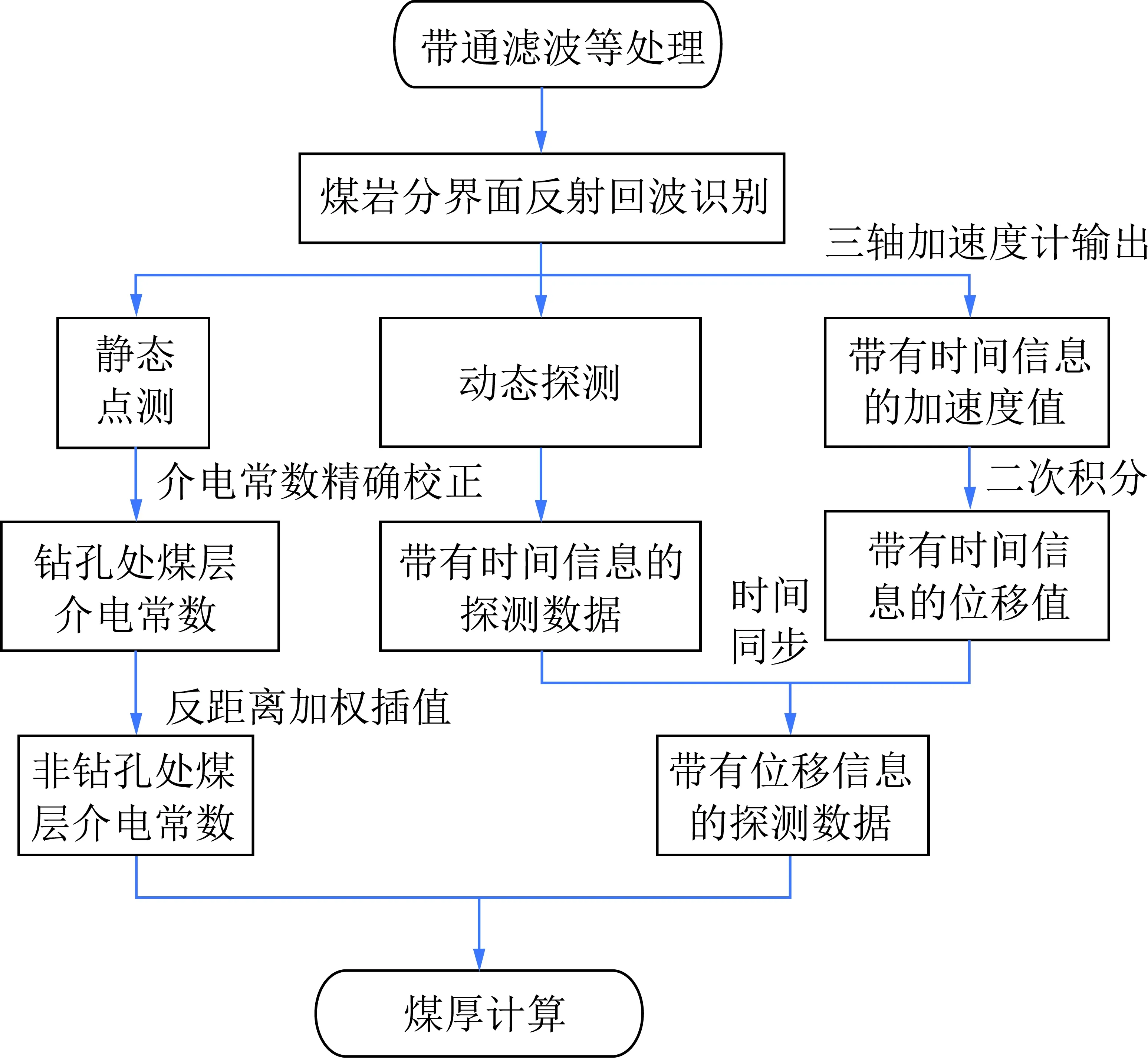
图2 特厚煤层厚度动态探测总体技术框架Fig.2 General technical frame diagram of dynamic detection of the thickness of extra-thick coal seam

(1)雷达信号处理。主要是通过带通滤波、调节增益、调节信号位置、去直流偏移等处理方式实现煤岩分界面反射回波的识别。

(2)介电常数精确校正。主要是使用探地雷达对钻孔处煤层进行静态点测，通过推导主机预设介电常数测得的煤层厚度与钻孔已知煤厚的关系对钻孔处煤层介电常数进行校正。

(3)预测钻孔之间煤层介电常数。主要是基于已校正的钻孔处煤层的介电常数，使用反距离插值算法预测钻孔之间煤层的介电常数。

(4)探测数据精确定位。主要是使用探地雷达对煤层进行动态探测，结合三轴加速度计、单片机、井下距离标记等对探测数据进行定位。

(5)煤厚信息准确计算。主要是利用步骤(3)得到的煤层介电常数信息与步骤(4)得到的带有位移信息的电磁波在煤层中的传播时间计算出煤厚。

3 特厚煤层厚度动态探测关键技术

3.1 介电常数精确校正技术

3.1.1钻孔处煤层介电常数校正

由式(3)可知影响探测煤厚准确性的关键参数是煤的介电常数。为此，在对煤层厚度进行动态测量之前，需要使用探地雷达测量各个钻孔所在位置处的煤岩界面信息，再根据钻孔已知煤厚信息对煤层介电常数进行校正。根据式(3)可知对于第i个钻孔，电磁波在煤层中的传播时间仅与该处煤层的实际介电常数有关。当主机设置的介电常数为任意值时，电磁波在煤层中的传播时间都相同。因此可以得到

(4)

(5)

联立式(4),(5)可得到校正公式为

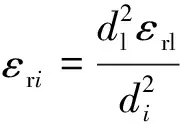
(6)

式中，εrl为探地雷达主机初始设置的介电常数;dl为探地雷达初始设置下测得的煤厚;di为钻孔图上第i个孔处已知的煤厚;εri为第i个孔处煤层校正后的介电常数。

3.1.2钻孔间煤层介电常数插值预测

影响煤层介电常数的因素有很多，煤层的组成成分、含水量、孔隙率等因素都会使煤层的介电常数有所差异。一般在同一工作面的煤层组成成分、含水量等基本相同，但夹矸层厚度却存在很大变化，这就导致不同区域煤层的介电常数会存在差异。

虽然钻孔间煤层的介电常数无法通过式(6)得到，但是由于煤层夹矸的形成一般符合一定的地质规律，因此可以利用插值方法来预测钻孔间煤层介电常数。反距离加权插值是一种常见的空间插值方法，广泛应用于空间预测和非线性插值。插值原理是以插值点与样本点之间的距离为权重进行加权平均，离插值点越近的样本点赋予的权重越大[19]，将样本点的值与其相对于插值点的权重依次相乘并求和即可得到插值点的值。

利用反距离加权插值来预测钻孔间煤层介电常数的计算过程如下:

(1)建立插值坐标系。将回风巷近似为直线，以回风巷靠近工作面一端为坐标原点，以插值位置为横坐标，介电常数值为纵坐标建立插值坐标系。

(2)建立反距离加权插值函数。

(7)

其中，εrx为插值点的煤层介电常数;n为钻孔数;λi为第i个钻孔处煤层介电常数的插值权重系数。λi需要满足归一化条件:

(8)

(3)计算反距离插值权重系数。反距离插值权重系数λi(i=1,2，…，n)表示插值点煤层介电常数与第i个钻孔煤层介电常数的接近程度，可表示为

(9)

li=|x-xi|

(10)

式中，li为插值点与第i个钻孔之间的距离;x为插值点的横坐标;xi为第i个钻孔点的横坐标。

(4)插值结果。根据校正后的钻孔处煤层介电常数以及各个钻孔所在位置，以1 m为插值间隔计算回风巷2 100～2 510 m的各个位置煤层的介电常数。

3.2 探测数据精确定位技术

现有的动态探测方式主要分为时间触发和测距轮触发。其中时间触发方式要求雷达天线按照设置的速度匀速前进，而井下环境恶劣，很难满足这一要求。测距轮触发虽然可以将行进距离与测量数据相结合，但由于巷道存在起伏并且探测机构在行驶过程中会偏离行驶路线，这都会导致测距轮测量的行进距离与理论行进距离存在很大差异，从而引起数据定位误差。为了克服时间触发方式无法应用于井下动态探测的缺陷，提出基于时间同步原则的动态探测数据定位方法，实现探测数据精确定位。

3.2.1基于三轴加速度计获取探地雷达位移原理

三轴加速度计能够感应3个方向(x轴、y轴、z轴)的加速度，并以一定的时间间隔输出[20]。由于加速度a是一个对象速度的变化速率，速度v是一个对象位移的变化速率，因此有

(11)

假设初始条件为0，则任意时刻的位移s都可以通过对a做二次积分得到，即

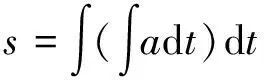
(12)

以加速度积分求得速度为例。由于三轴加速度计获取的加速度是关于时间的离散数据，在对加速度进行积分之前，必须先对加速度进行曲线拟合处理。如图3所示，tj为第j个时间间隔对应的时刻，k为雷达探测的总时间间隔，雷达任意时刻的速度可以表示为对应时刻曲线下方与坐标轴包围的面积大小。因此，速度v可近似表示为

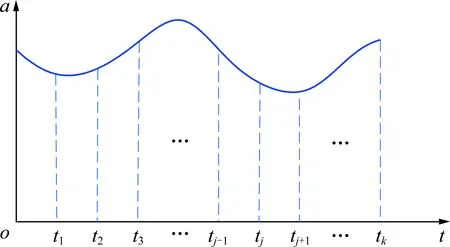
图3 加速度求解速度示意Fig.3 Diagram of velocity calculation using acceleration

(13)

式中，aj为第j个时间间隔采集到的加速度;Δt为三轴加速度计的采样时间间隔。

同理，可通过再次积分求得任意时刻的位移s。

3.2.2三轴加速度计在探测装置上的安装设计

为准确测量出雷达天线的位移，将三轴加速度计安装在探测小车中，保证三轴加速度计的x方向为风门至工作面方向，y方向为垂直于回风巷两侧煤壁方向，z方向为垂直回风巷顶煤方向。三轴加速度计在探测装置上的安装示意如图4所示。

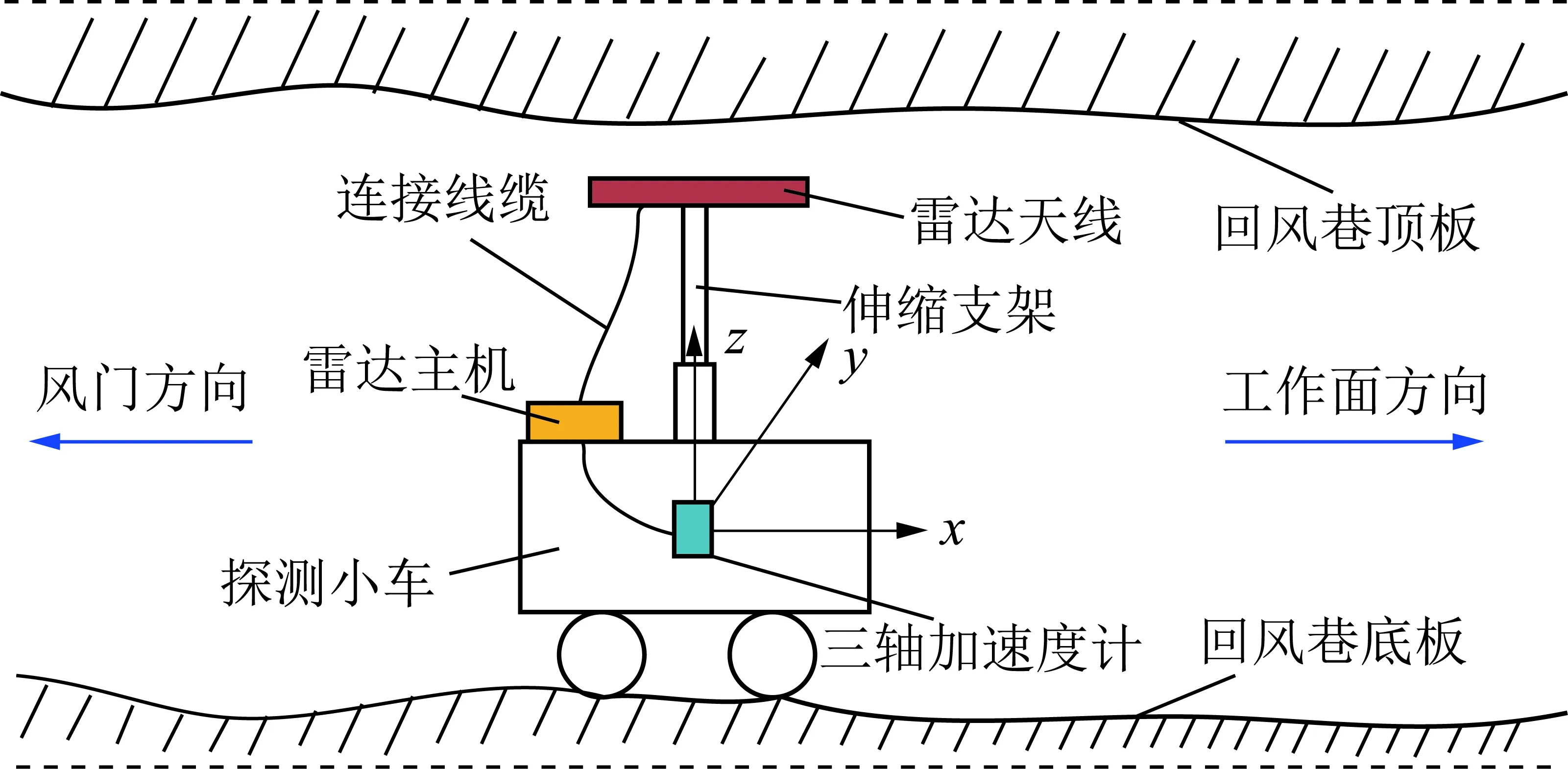
图4 三轴加速度计安装示意Fig.4 Installation diagram of three axis accelerometer

3.2.3探测数据精确定位

在进行煤厚动态探测的过程中，笔者采用三轴加速度计测量探地雷达天线加速度，并输出到单片机进行记录，然后对位移进行计算。雷达主机在天线经过井下距离标记时对探测数据进行打标处理，在探测结束以后根据距离标记对应的时间对雷达位移进行校正，以减少误差的叠加，实现探测数据精确定位。具体流程如图5所示。

图 5 探测数据定位流程Fig.5 Flowchart of location of detection data

(1)三轴加速度计测量单位时间间隔的加速度ax，ay，az并输出到单片机中，与此同时，主机开始记录天线的探测数据。主机记录的数据量m与时间有如下关系:

m=VT

(14)

式中，V为总扫描速度;T为总扫描时间。

(2)根据设定算法对三轴加速度计x方向位移s进行计算，得到位移与时间的对应关系。

(3)在经过井下距离标记时，操作主机对探测数据进行打标处理。

(4)根据打标所记录时间，对相应时刻天线的位移进行更新，以此减小三轴加速度计测位移的累积误差。

(5)完成特厚煤层厚度动态探测后，基于时间同步原则将探测数据与位移进行匹配，确定每个时刻的位移所对应的探测数据信息。

4 试验与结果分析

4.1 测区概况

山西省大同市云冈区塔山矿8222工作面长230.5 m，煤层倾角为1°～4°，煤层较为稳定。煤层以烟煤为主:黑色、半亮型煤，碎块状、块状、条带状结构，弱玻璃光泽、沥青光泽，水平层理，含层状夹矸层。8222工作面回风巷全长2 644.5 m，目前已推进2 080 m。由于探地雷达的探测深度和分辨率都与天线主频率有关，根据矿方提供的钻孔地图可知:8222工作面回风巷剩余部分的煤厚变化范围为7.72～13.41 m，为满足探测深度要求并获得良好的探测精度，选择天线主频率为100 MHz的天线进行探测，该天线最大探测深度为30 m。

4.2 介电常数精确校正

本次煤层介电常数的校正共选取4处钻孔，分别为2 100，2 200，2 300以及2 400 m处钻孔。以回风巷的2 100 m处钻孔煤厚信息为例，此处钻孔煤厚为10.34 m，探地雷达初始设置的介电常数为3.5，初始设置下测得的煤厚为9.72 m，测量误差为6.00%。将以上数据代入式(6)得到校正后的介电常数为εr1=3.5×9.722÷10.342≈3.09。现场探测图如图6所示，2 100 m处探地雷达探测波形信息如图7所示。

图6 现场探测Fig.6 Layout of field experiments

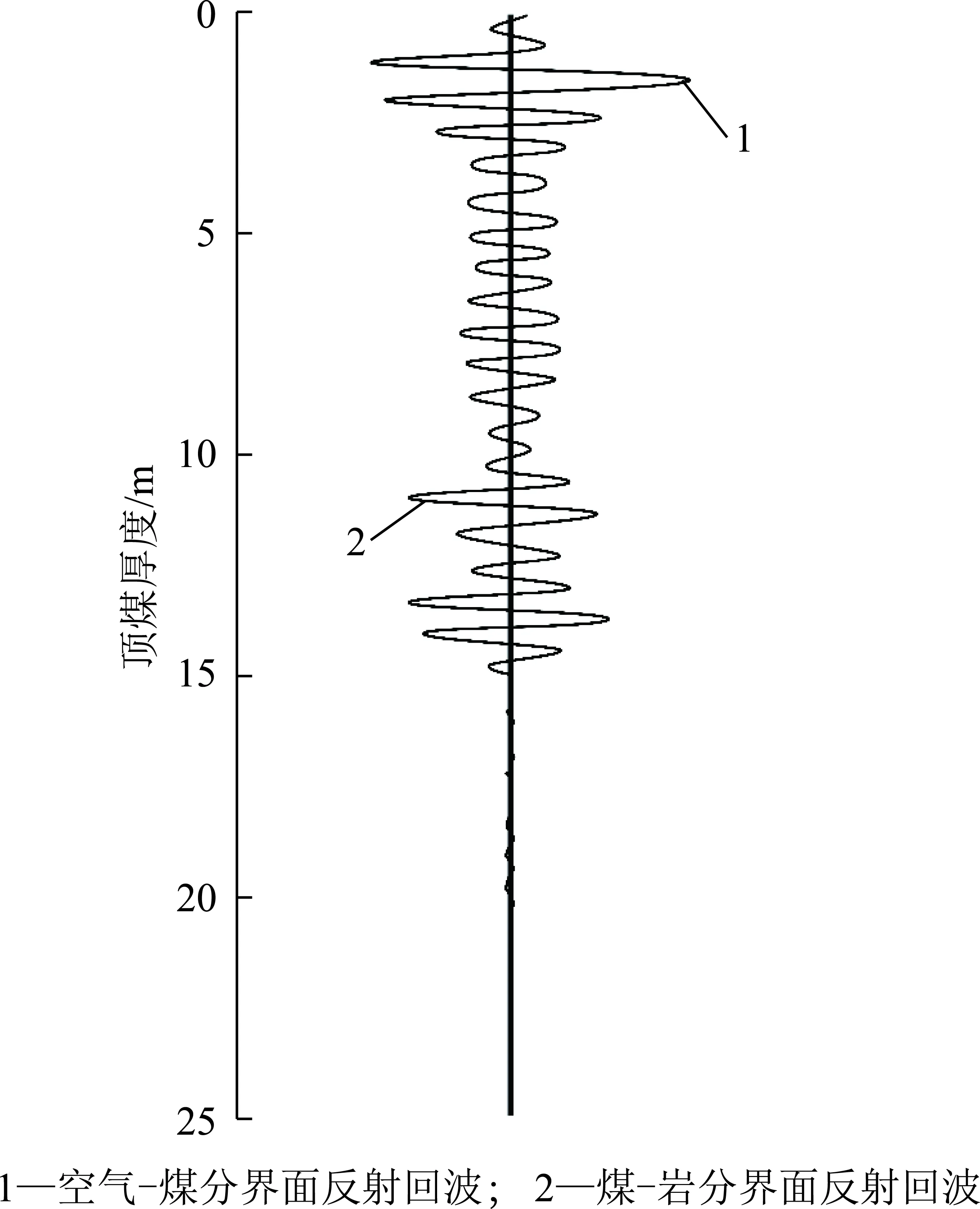
图7 2 100 m处雷达探测图像Fig.7 Radar detection image at 2 100 m

从图7可以看出，单道波形图中存在较多同相轴，其主要原因是由于特厚煤层中夹矸层数较多，而夹矸与煤的介电常数有差异，电磁波传播过程中会在煤-夹矸分界处形成反射回波。但煤与岩的介电常数差通常大于煤与夹矸的介电常数差，即煤-岩分界面反射回波幅值会大于煤-夹矸分界面反射回波幅值。由此可见，1处正相位幅值最大，分析是空气-煤分界面反射回波;2处负相位幅值明显大于上面的几处负相位幅值，分析是煤-岩分界面回波;2处以下的回波，分析是岩石与其他介质的分界面回波。

同理可计算出其他3个钻孔位置煤层对应的校正后的介电常数，校正结果见表1。

从表1中可以看出，在对煤层介电常数进行校正前，使用经验的煤层介电常数对钻孔处煤层厚度进行探测时，探测误差最大为10.49%，最小为4.10%。随着钻孔处煤层厚度的增加，校正后的煤层介电常数值会逐渐增大，产生该现象的主要原因是随着煤厚的增加夹矸的厚度也相应增加。

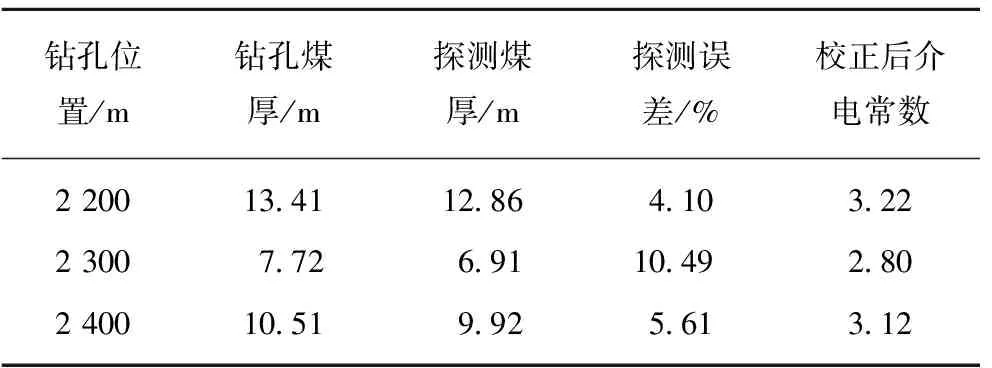
表1 钻孔处校正后的介电常数Table 1 Corrected dielectric constant at borehole

在对各个钻孔处煤层介电常数进行校正后，对相邻钻孔间煤层的介电常数进行插值预测，插值间隔为1 m，得到回风巷煤层介电常数插值曲线图，如图8所示。

图8 介电常数插值Fig.8 Interpolation curve of dielectric constants

4.3 动态探测试验

将探地雷达调整为连续探测模式对回风巷煤层厚度进行动态探测，以2 200 m处钻孔附近的一段连续测量数据为例，分析探地雷达回波信息。探测灰度图如图9所示。

图9 2 200 m附近动态探测灰度Fig.9 Gray scale image of dynamic detection near 2 200 m

从图9可以看出，空气-煤界面的反射信号与煤-岩分界的反射信号都是连续的，而它们之间有很多间断反射信号，结合夹矸的不连续性，分析中间的间断的反射回波为夹矸层与煤分界面所产生的反射回波。因此，在动态探测时可以根据回波是否连续来区别夹矸-煤界面与煤层-顶底板界面，实现煤-顶板界面与煤-矸界面的有效分辨。

4.4 工作面钻孔数据与探测数据对比

为验证特厚煤层厚度动态探测的探测精度，将探地雷达测量的煤厚信息与工作面内回采过程中靠近回风巷的钻孔数据进行比较，结果见表2。

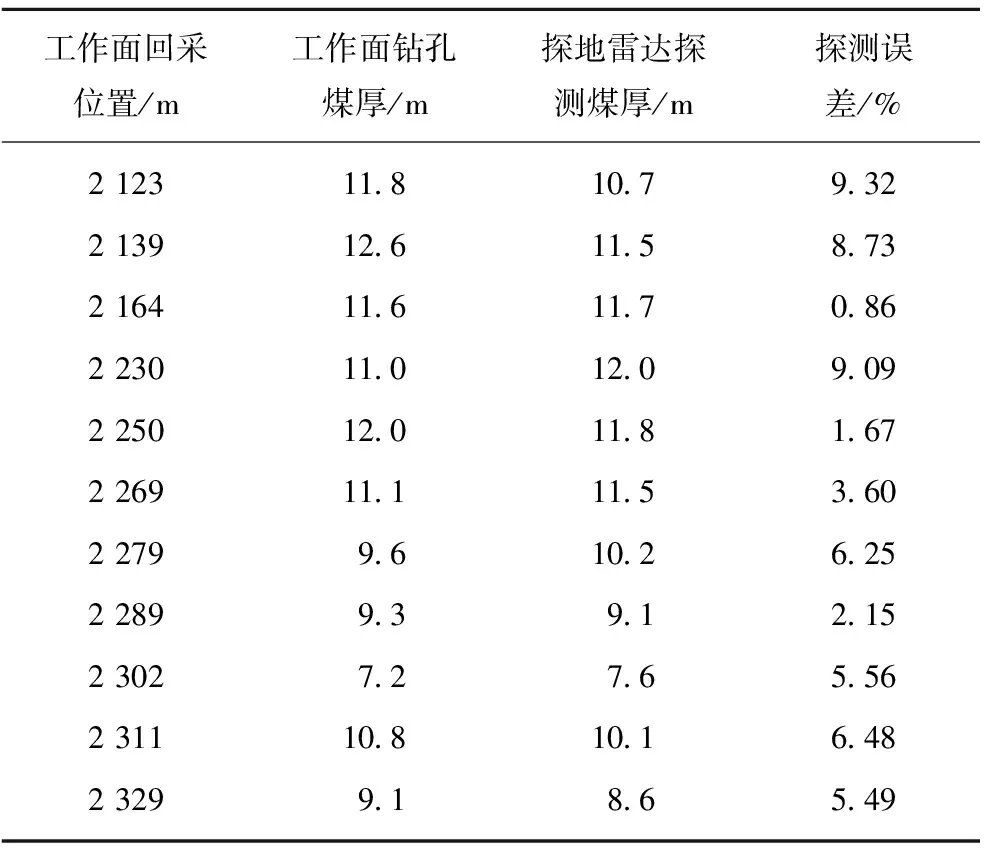
表2 工作面钻孔数据与探测煤厚比较Table 2 Comparison between borehole data and detecting coal thickness in working face

由表2可知，经过煤层介电常数精确校正与探测数据定位之后，钻孔煤厚与探地雷达所测煤厚相差不超过10%。煤层厚度最大探测误差为9.32%，最小探测误差仅为0.86%，远远小于现有煤层三维模型的垂向建模误差，基本满足了现有煤层三维模型局部修正的精度需求。

4.5 与单一介电常数煤厚探测技术对比试验

为了验证煤层介电常数插值技术相对于现有技术(使用单一介电常数进行煤厚计算)是否具有优势，又开展了与使用单一介电常数煤厚探测技术对比试验，即利用探测数据与上述煤层介电常数校正结果分别计算当煤层介电常数为3.09，3.22，2.80，3.12时对应的煤厚值，结合工作面钻孔数据计算得到对应的探测误差，并绘制误差对比图，结果如图10所示。

从图10可以看出，介电常数为3.22，2.80，3.12时，使用单一介电常数煤厚探测技术的煤厚最大探测误差均大于10%，虽然当介电常数为3.09时，煤厚最大探测误差小于10%，但其误差波动范围与最大误差均大于煤层介电常数插值技术。

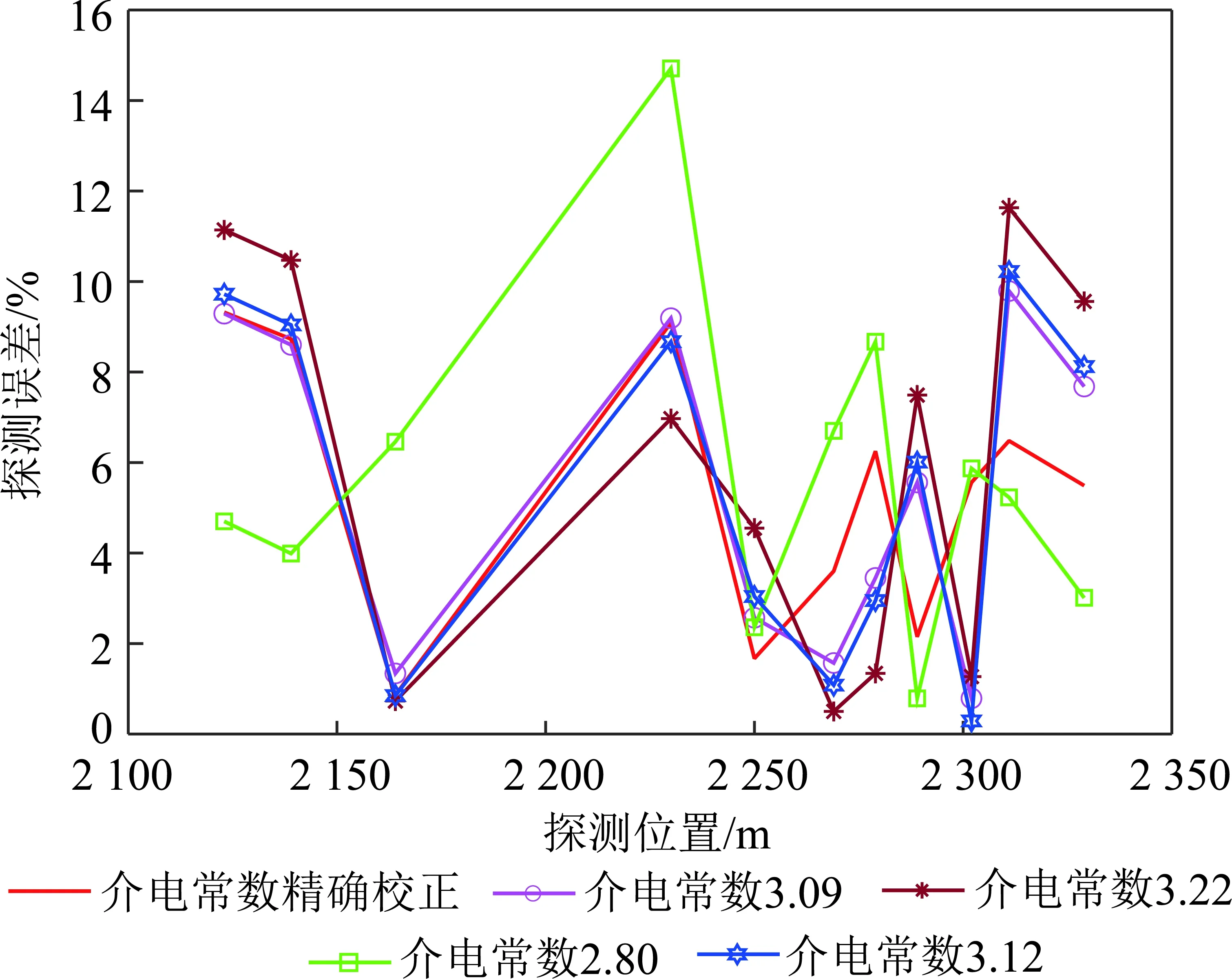
图10 煤厚探测误差对比Fig.10 Detection error comparison of coal thickness

4.6 回风巷煤层三维模型构建

为验证本文所提出的方法可为煤层三维模型两巷区域的局部修正提供基础数据，根据计算出的回风巷各处煤层厚度得到回风巷煤厚的线性变化趋势，为了更为直观地呈现回风巷煤厚的变化趋势，建立回风巷局部区域2 100～2 510 m对应的煤层三维模型(图11)。

图11 回风巷局部区域煤层三维模型Fig.11 Three-dimensional model of coal seam at the local area of return air roadway

由图11可知，在回风巷2 280～2 310 m段的特厚煤层厚度变化幅度较大，其他位置煤厚变化较平稳。以探地雷达连续探测数据建立的回风巷煤层模型可用于对初始煤层三维模型局部区域进行修正，提高初始煤层三维模型的局部精度。

5 结 论

(1)在进行特厚煤层厚度探测的过程中，使用单一介电常数进行煤厚计算时容易引起较大误差，需要对各处煤层介电常数进行计算。

(2)提出的基于时间同步原则的探测数据定位技术可以将探地雷达所测煤岩分界面信息与雷达位移结合起来，为恶劣环境下探地雷达的数据定位提供了新方法。

(3)试验结果证实了提出的特厚煤层动态探测技术可以对回风巷的特厚煤层厚度进行高效率探测，并且可以保证一定的探测精度，在此基础上可以建立回风巷煤层三维模型，为初始煤层三维模型局部精确修正提供基础数据。