α-平稳Cox-Ingersoll-Ross模型的参数估计

魏超，何朝兵

（安阳师范学院，数学与统计学院，河南 安阳455000）

0 引言

在现实世界中，几乎所有的现象都或多或少受到噪声的影响，表现出一定的随机特性。随机微分方程是研究随机现象的重要工具，广泛应用于物理、化学、医学等领域随机现象的建模［1-2］，尤其是近些年来，随机微分方程成为金融领域随机现象建模的基本工具，常被用来描述金融资产的价格动态、资产的证券投资组合和利率的期限结构［3-4］。在建立定价公式时，随机模型中的参数描述了相关资产动态。然而，通常情况下，参数往往是未知的。因此，为了更好地掌握相关资产动态，对未知参数的估计成为亟待解决的关键性问题。在过去的几十年里，学者们对随机金融模型进行了参数估计问题的研究，并取得了一些显著的成果。例如，Yu 和Phillips［5］用Gaussian 估计法研讨了一般非线性连续时间短期利率模型的参数估计，以Cox-Ingersoll-Ross 模型为例给出参数估计量并进行了模拟，结果表明估计方法有效。Faff 和Gray［6］用一般矩估计法讨论了均值回归短期利率模型的参数估计，并给出Chan-Karloyi-Longstaff-Sanders 模型参数估计量的模拟结果。Wei 和Shu［7］运用极大似然估计法分析了非线性时齐随机系统参数估计量的存在性、相合性以及估计误差的渐近正态性。Hu［8］等学者分析了分数布朗运动驱动的非线性随机微分系统最小二乘法估计量的强相合性。Wei［9］运用极大似然估计法和卡尔曼滤波理论相结合，研究了不完全观测下非线性随机模型的参数估计。

Cox-Ingersoll-Ross 模 型 是Cox，Ingersoll 和Ross 三位学者在1985 年提出的短期利率模型［10-11］。Cox-Ingersoll-Ross 模型把期限结构看作是一种随机过程，它是利率的一种总体均衡模型，该模型的优势在于它包含了风险回避、时间消费偏好、财富限制、导致风险补偿的因素和众多的投资选择。Cox-Ingersoll-Ross 模型保证了利率的均值回归，避免了利率取负值的可能性。在过去的几十年里，一些学者研究了Cox-Ingersoll-Ross 模型的参数估计问 题。例 如，Rossi［12］运 用 滤 波 理 论 分 析 了Cox-In⁃gersoll-Ross 模 型 的 参 数 估 计。Alaya 和Kebaier［13］运用最小二乘法讨论了遍历和非遍历情况下模型的参数估计。Li 和Ma［14］利用最小二乘法研究了参数估计量的渐近性质。Wei［15］等学者运用Gaussian估计法给出漂移项和扩散项参数估计量和估计误差的解析表达式，并证明了估计量的强相合性。Wei［16］利用最小二乘估计法研究了小平稳对称噪声驱动的Cox-Ingersoll-Ross 模型的参数估计。Barc⁃zyi［17］等 学 者 分 析 了Heston 模 型 最 小 二 乘 估 计 量 的渐近性质，并以Cox-Ingersoll-Ross 模型为例进行了数值模拟。虽然学者们在Cox-Ingersoll-Ross 模型参数估计方面取得了一些成果。但是，大多数成果是建立在布朗运动驱动的随机模型上，而关于非高斯白噪声影响的随机模型的研究却少见报道。而且，很多金融过程展现出非连续样本路径和重尾性质，布朗运动驱动的Cox-Ingersoll-Ross 模型无法刻画这些特性，所以需要用Lévy 过程替换布朗运动［18-19］。因此，研究α-平稳Lévy 噪声影响下Cox-Ingersoll-Ross 模型的参数估计问题具有重要的理论和实际意义。本文运用最小二乘法研究了离散观测下严格对称α-平稳Lévy 过程驱动的Cox-In⁃gersoll-Ross 模型的参数估计问题，给出漂移项参数估计量的解析表达式，证明了估计量的强相合性并通过数值模拟验证了估计量的有效性。

本文的内容安排如下：第1 部分介绍了α-平稳Lévy 过程驱动的Cox-Ingersoll-Ross 模型并得到估计量的解析表达式；第2 部分证明了估计量的强相合性；第3 部分给出估计量和估计误差的数值模拟结果；结论在第4 部分给出。

1 问题描述

本文研究离散观测下α-平稳Cox-Ingersoll-Ross 模型的参数估计问题。因此，我们首先给出α-平稳过程的定义。

定义1［20］令参数α，σ，β，μ满足：α∈(0，2]，σ∈(0，+∞)，β∈[-1，1]，μ∈(-∞，+∞)，且

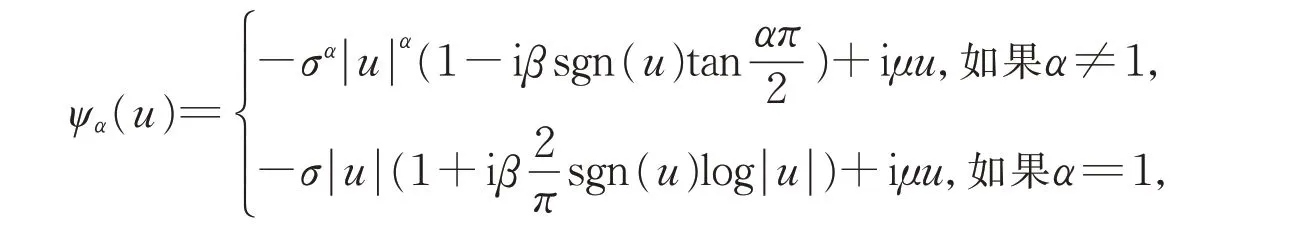
其中u∈(-∞，+∞)，i2=-1。如果随机变量η有特征函数Eeiuη=e-Ψα(u)，则η～Sα(σ，β，μ)，即η有一个α-平稳分布。当μ=0 时，η严格α-平稳，如果再加上β=0，则η对称α-平稳。如果对任意的0≤s＜t，满足

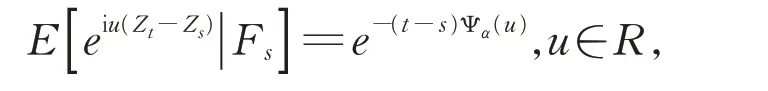
则{Ft}-适应过程Z={Zt，t≥0}是一个α-平稳过程。α-平稳过程是一个伴有平稳和独立增量的Markov过程。

令(Ω，F，P)为带流{Ft，t≥0}的概率空间，Z={Zt，t≥0}为概率空间(Ω，F，P)上严格对称的α-平稳Lévy 过程，且假设指标α∈(1，2]。如果α=2，则Z为布朗运动。

现在，我们给出α-平稳Cox-Ingersoll-Ross 模型的表达式：

其中θ和λ是未知参数，且θ＞0，λ＞0，Z={Zt，t≥0}为严格对称的α-平稳Lévy 过程。我们建立如下对照函数：

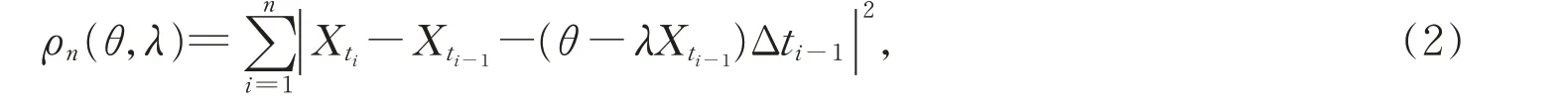
其中Δti-1=ti-ti-1=h。

用最小二乘法得到如下方程组：

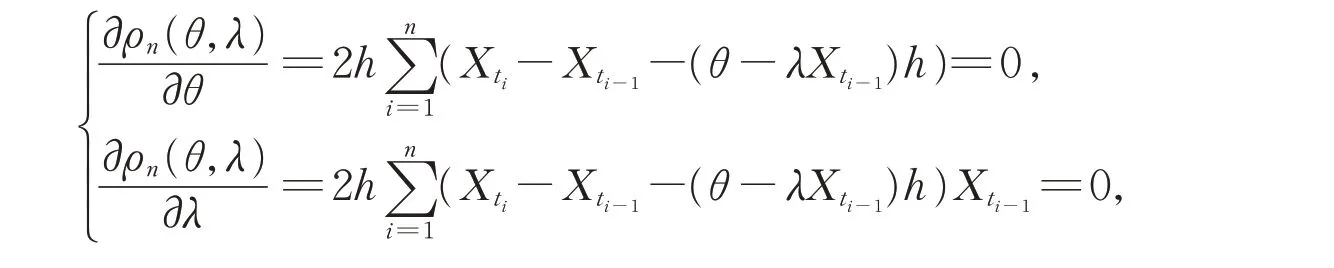
即

2 主要结论

根据（1）式可以得出：

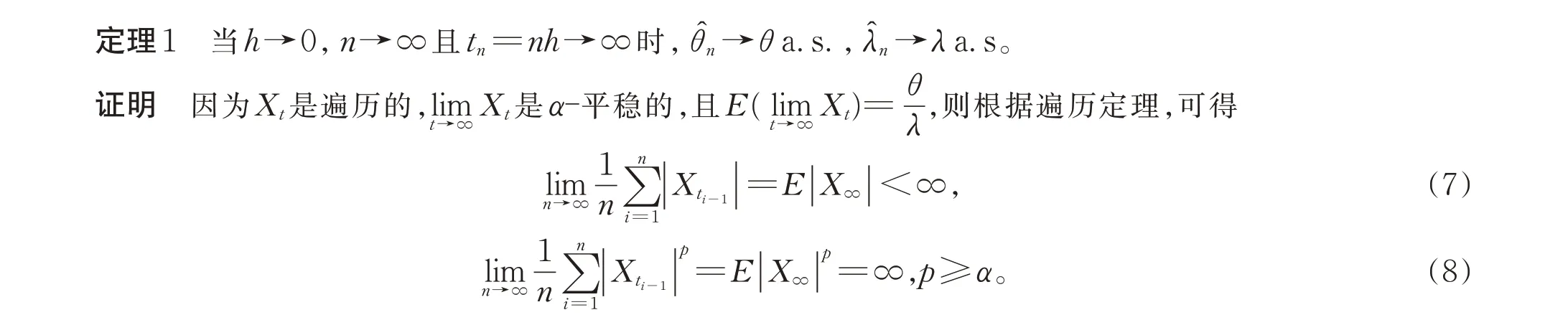
因为

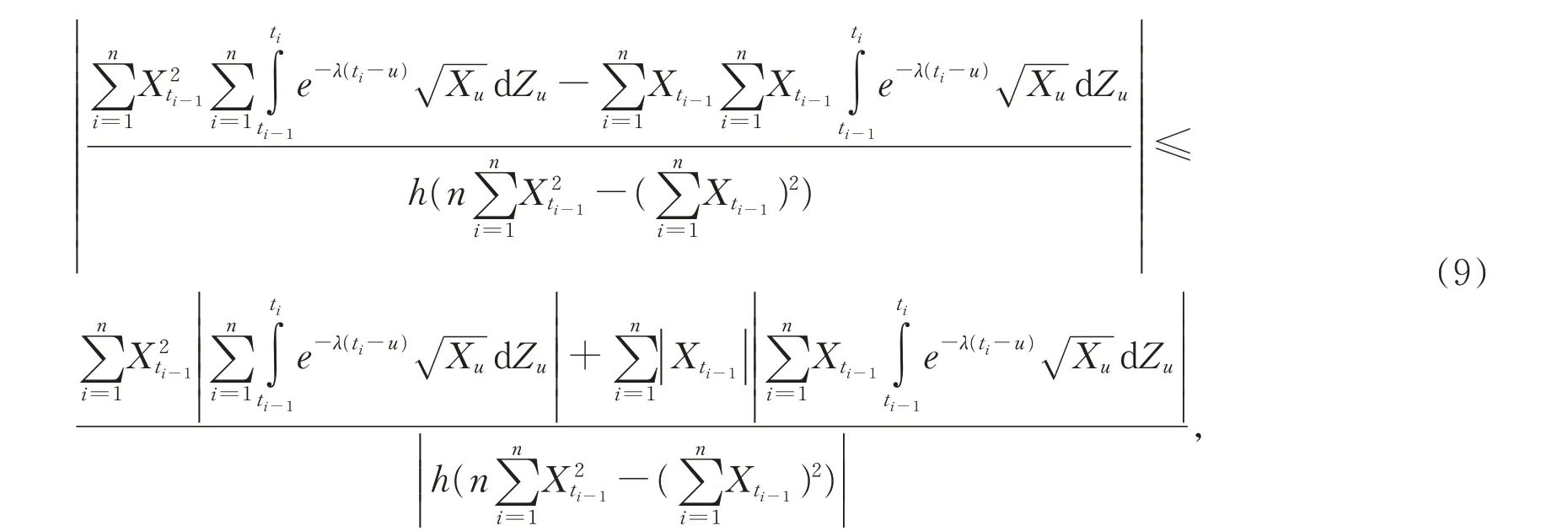
而且，根据（7）式和（8）式以及文献［21］中推论3.1，可得

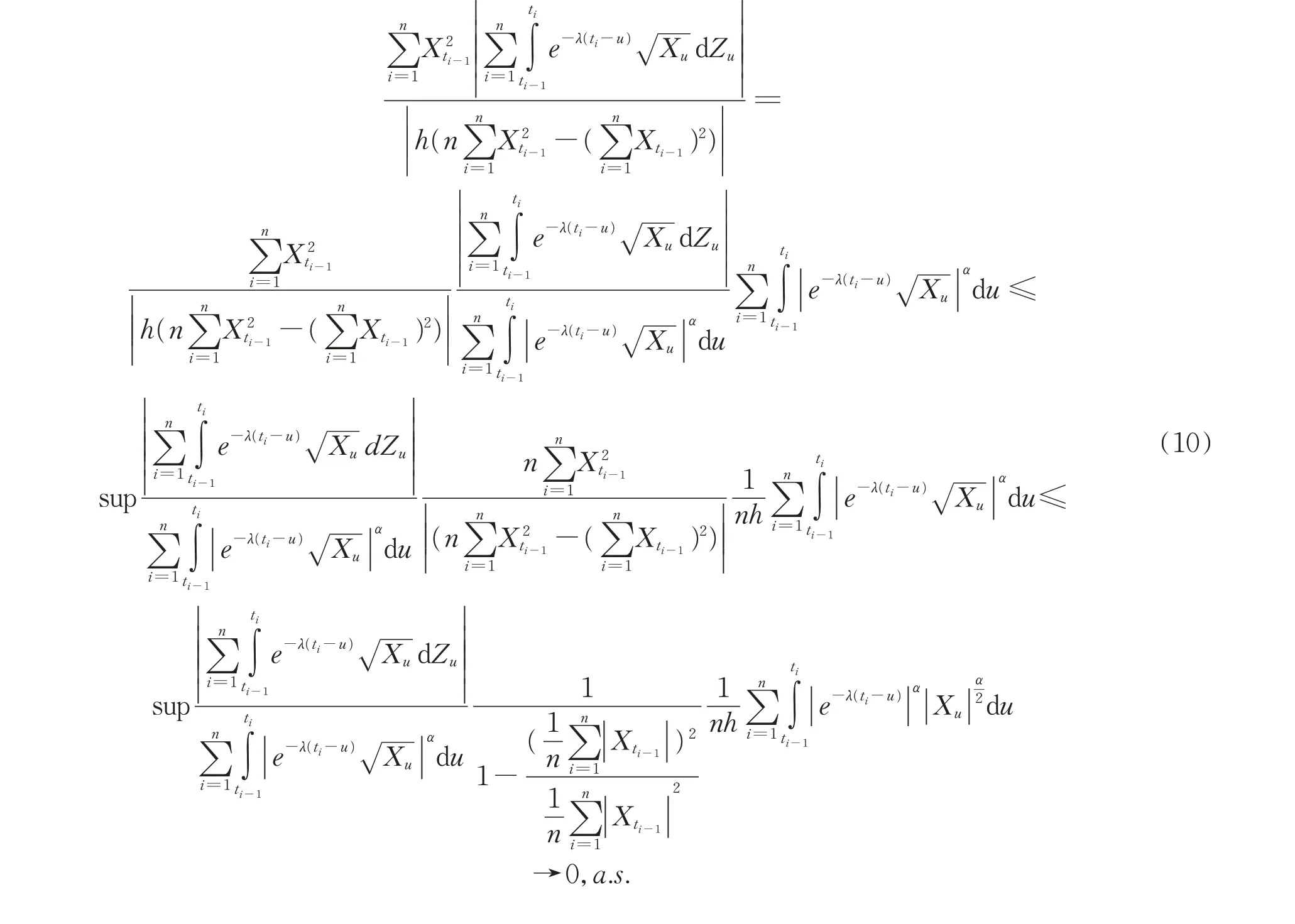
且

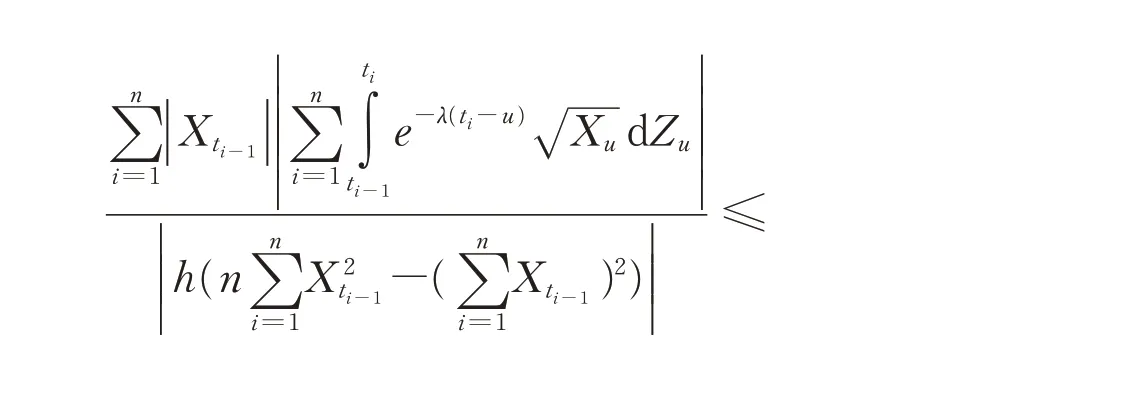
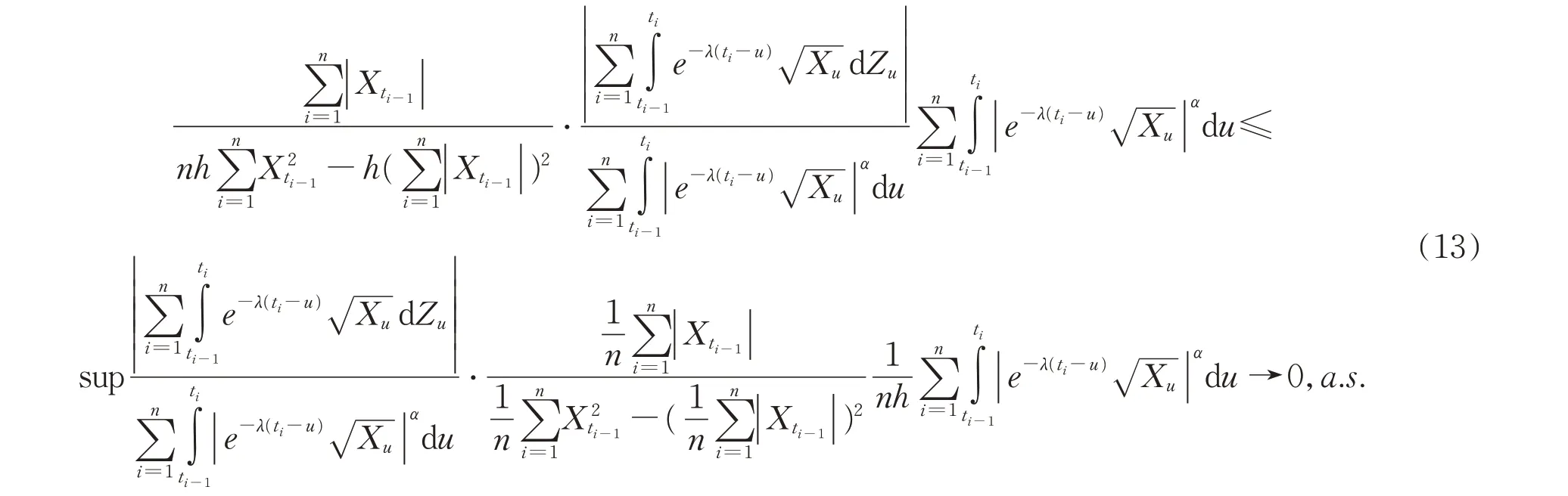
根据Holder 不等式，

根据（12），（13）和（14）式，当h→0，n→∞且tn=nh→∞时，可得λ̂n→λa.s.。

综 上 所 述，我 们 证 明 了 参 数 估 计 量θ̂n和λ̂n的 强相合性。

3 模拟

这 一 部 分，我 们 给 出 估 计 量θ̂n和λ̂n的 数 值 模 拟结果。令α=1.5，x0=1。在表1 中，令h=0.1，样本值n从1 000 到5 000。表2 中，令h=0.01，样本值n从10 000 到50 000。两个表均列出了估计量和估计误差的模拟结果。结果表明，估计量和参数真值之间没有明显的差别，估计量很好。

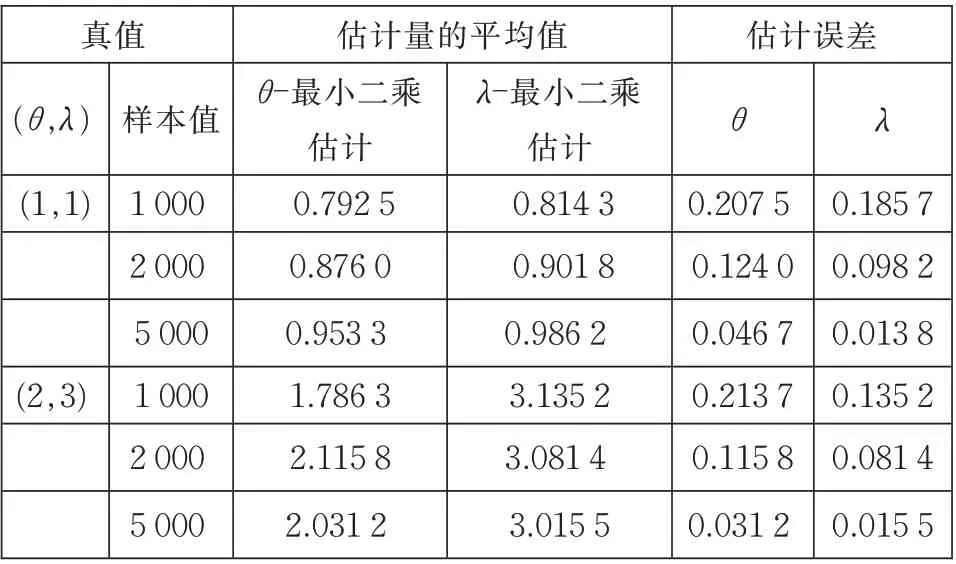
表1 θ和λ的最小二乘估计模拟结果（h=0.1）Table 1 Simulation results of least square estimation of θ and λ（h=0.1）

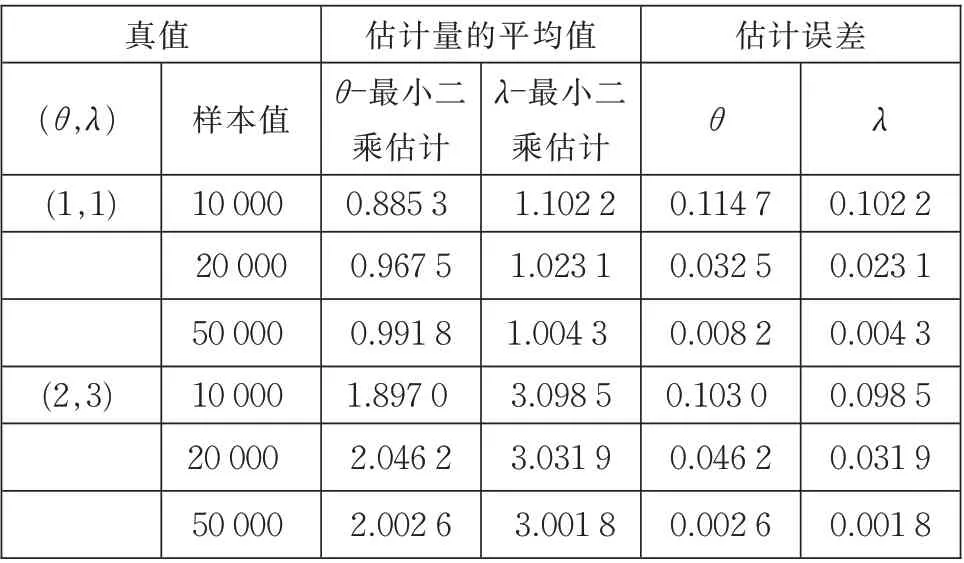
表2 θ和λ的最小二乘估计模拟结果（h=0.01）Table 2 Simulation results of least square estimation of θ and λ（h=0.01）

4 结论

本文的目的是研究离散观测下严格对称α-平稳Lévy 过程驱动的Cox-Ingersoll-Ross 模型的参数估计问题，并讨论估计量的渐近性质。由于模型的复杂性，我们建立对照函数，并求得参数的最小二乘估计量。利用遍历定理、Holder 不等式及α-平稳Lévy 过程的性质，分析了漂移项两个参数估计量的强相合性。通过数值模拟，证明了估计量是有效的，估计量很好。