电子在金属-应变石墨烯异质结中的传输

郭敏，闫维贤

（1. 山西大学 理论物理研究所，山西 太原030006；2. 山西大学 物理电子工程学院，山西 太原030006）

0 引言

近十几年来，单层碳原子石墨烯［1-2］的发现激发了人们对开发各种类型的二维材料的热情。物理学家寄希望于石墨烯来革新下一代电子应用并且使在不同领域的物理学科，比如高能物理和凝聚态物理之间架起桥梁。类似于半导体异质结构，石墨烯异质结构在探索石墨烯光电特性的理论和实验方面也是很有前途的候选者。有许多研究小组对石墨烯量子阱［3-7］，超晶格［8-11］和石墨烯量子点［12-13］展开过研究，例如不同磁场（矢量势）［10-11］以及不同势阱和势垒［14-18］组成的石墨烯量子阱和超晶格；限域于矢量势以及静态和含时电势中的石墨烯量子点［12-13］；石墨烯与超导层异质结构的邻近效应所引起的镜面安德列夫反射［14-15］。就石墨烯电子传输的测量而言，金属接触不仅充当电子储集层［16］，而且是金属和石墨烯接触边界周围散射的主要来源［17-18］，因此对金属-石墨烯异质结构周围的散射进行研究是非常必要的。有物理学家在紧束缚方法的框架下，对于低能量状态下的电子在普通金属-石墨烯界面处的传播模式以及瞬逝模式进行了定量分析［17］。我们在本文中将应力纳入了石墨烯一侧［19-20］，并研究了石墨烯中的应力对普通金属-石墨烯接触处散射的影响。得到了普通金属-石墨烯界面的反射系数的解析表达式。通过数值计算，分析了最大透射系数（以及相应角度）随有效界面跳跃积分、入射能量以及应力的变化趋势。此外，对正常金属和石墨烯两侧的波函数随应力变化的情况进行了研究，并用纵向动量匹配来解释了一些波函数出现的有趣现象。

我们的具体工作如下，在第1 部分我们对加入了应力后的正常金属-石墨烯模型进行了讨论，第2部分集中于对透射的数值计算与分析，第3 部分总结了我们的工作。

1 普通金属-石墨烯异质结构模型的分析

2 反射系数的计算

假设石墨烯中位于r处的子晶格A，B的赝自旋旋量为ψg(r)=(da(r)，db(r))T，金属与应力石墨烯异质结构的界面处的波函数之间的关系由以下方程式定义：

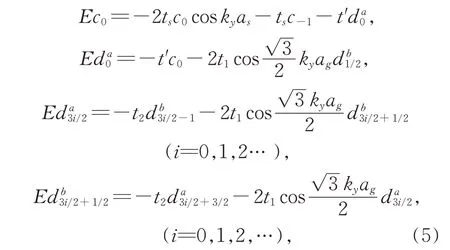
其中，t1，t2代表应力石墨烯中的跳跃，t′代表金属和应力石墨烯异质结构交界处的跳跃，此处已经考虑了应力对跳跃积分的影响。当从金属侧有入射波eiks xeiqs y传播且传到石墨烯一侧并在金属/石墨烯界面反射，则在金属晶格r位置处的波函数为c(r)=(eiks x+re-iks x)eiqs y，由于在应力石墨烯侧只有出射波，

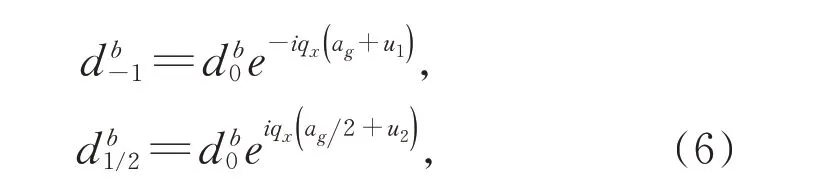
其中，u1和u2之前已定义，并在图1 的右侧的示意图进行了说明。通过使用方程（5）与（6），可以得到以下等式

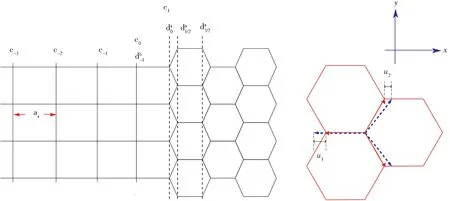
图1 左侧图：金属-石墨烯异质结构，其中系数cj，dj 分别代表了金属，石墨烯在晶格上的波函数。右侧图：3 个红色的实线向量代表了原始石墨烯最近邻的向量基(i=1，2，3)，3 个蓝色的虚线向量代表了应力石墨烯最近邻的向量基δ(i=1，2，3)，且u1 和u2 为 沿x 方 向 上 的 长 度 改 变Fig. 1 Left side:the metal-graphene heterostructure where the coefficients cj and dj represent the on-site wavefunctions for metal and strained graphene respectively;Right side:three red solid vectors are nearest-neighbor vector basis (i=1,2,3)for pristine graphene,while three blue dashed vectors are nearest-neighbor vector basis (i=1,2,3)for strained graphene,u1 and u2 are the length changes along x direction

3 数值分析和讨论

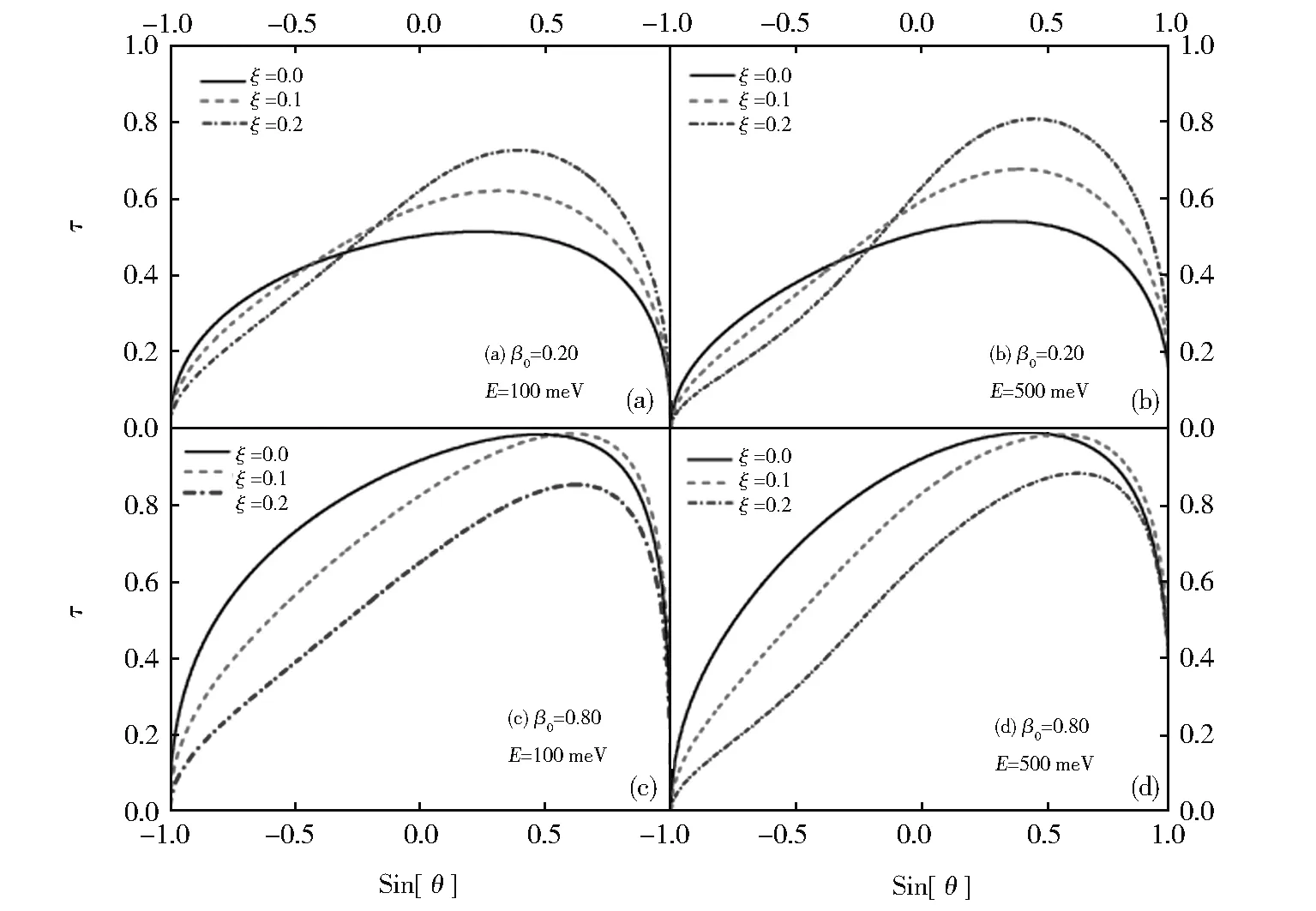
图2 对于入射能量分别为E=100 meV 和500 meV，在ξ=0.0（无应力）、0.1、0.2 的不同应力强度情况下，透射τ =1-R与Sin[θ]的关系图，（a）β0=0.2，E=100 meV（b）β0=0.2，E=500 meV，（c）β0=0.8，E=100 meV，（d）β0=0.8，E=500 meVFig. 2 Transmission τ ≡1-R against sin[θ]under the different strain cases of ξ =0.0(strainless),0.1,0.2 for two incident energies E=100 meV and 500 meV,respectively;(a)β0=0.2,E=100 meV(b)β0=0.2,E=500 meV(c)β0=0.8,E=100 meV(d)β0=0.8,E=500 meV

为了进一步明确应石墨烯是如何影响电子透射性能的，我们研究了E，β0，ξ这几个参数对电子最大透射的影响。图3 画出了在入射能量为100 meV的条件下，应力强度ξ分别为0、0.1、0.2 时，最大透射率τm以及对应的入射角度θm(Sin[θ])随金属-应力石墨烯交界面跳跃参数β0变化的关系图。对于不透明的界面（β0=0），隧穿确实会被完全阻止，但正如图中所示，增加β0也并不一定会改善隧穿。

图3 在应力ξ 分别为0.0、0.1、0.2 且入射能量为E=100 meV 的三种情况下，图中上下两部分分别表示了随界面跳跃积分参数变化而变化的最大透射率τm 和所对应的角度θm(Sin[θ])，最佳透射τoptm 指的是τm 的峰值Fig.3 Maximum transmission τm and the corresponding angle θm(Sin[θ])against the interface hopping β0 are shown in the upper and lower panels,respectively under three cases of strain ξ=0.0,0.1,0.2 and the incidence energy of E=100 meV,the optimum transmission τoptm refers to the peak value of the τm

在无应力的情况下，电子的τoptm也就是最大透射率的峰值出现在β0取1 时，而在应力参数分别取0.1、0.2 时，最 大 透 射 率 的 峰 值 分 别 出 现 在β0取0.69 和0.5 时。随着应力的增加，最佳透射出现的位置向β0减小的方向移动。同时最佳入射角度θoptm随着应力的增加而增加（远离θ=0°）。当界面跳跃参数β0增大到超过最佳透射对应的数值，透射将被快速地抑制，而且应力的引入加剧了这一现象。相对应的最大透射角θm接近θ=0°方向且当界面跳跃取更大的值时，增大应力对最大透射角度的影响可忽略不计。

图2 表明，粒子入射能量的改变对电子穿透界面的能力没有明显的影响。我们为了更进一步探究这种情况产生的原因，在图4 中画出了入射能量E和最大透射率τm的示意图来解释此原因。通过观察图4 的上半部分，我们发现当β0=0.2 时，应力确实可以促进透射，这可以通过比较有应力和无应力时最大透射的斜率变化来验证。对于无应力情况，曲线斜率可以忽略不计，但施加应力后会增加曲线斜率。尽管入射能量的增加对透射能力的增加帮助很小，但无论如何，入射能量的增加都会增加透射能力，而且这种能力受应力的调制。

图4 在β0 取值为0.2 的前提下，上下两部分图示分别表示了在不同的应力的情况下，即ξ 的取值为0.0、0.1、0.2 时，最大透射率τm 和最大入射角Sin[θm]随着入射能量的的变化情况Fig. 4 Maximum transmission τm and the corresponding angle Sin[θm]against the incidence energy E are shown in the upper and lower regions respectively under three cases of strain ξ=0.0,0.1,0.2 and the interface hopping β0 is set to 0.2

金属侧和石墨烯侧边界晶格上的有效波函数可以通过以下两个方程式确定（请参见图1 左侧所示）：

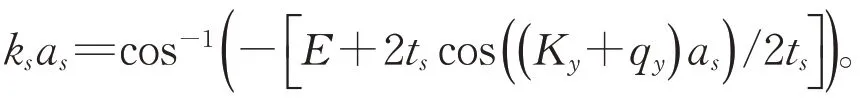
图5 在金属格点和石墨烯格点侧的波函数，带有正方形符号的线代表波函数的实部，而带有圆点符号的线代表波函数的虚部Fig. 5 Wave functions on lattices of metal and graphene sides,the line with square symbol(red-solid)stands for the real part of the wave function,while the line with dot symbol(blue-dashed)stands for the imaginary part of the wave function

4 结论

通过数值和解析方法，研究了电子在金属-石墨烯（应力）异质结构下的传输特性。通过分析最大透射率和对应角度与应力强度、入射能量和有效界面的跳跃参数关系，研究了该异质结的传输特性。我们发现，对石墨烯应力的引入可以显著地改变电子的透射能力，透射能力的大小取决于施加的应力和有效的界面跳跃的大小。入射能量的增加对电子透射性能的影响不大，可忽略不计，却可以使最大透射角增大。我们还研究了不同应力下波函数的实部和虚部是如何演化的，通过研究发现施加在石墨烯侧的应力的增加可以使金属侧的波函数的周期增加，这可以用纵向动量匹配来解释。通过这一研究我们发现这些结果可以用来定性研究金属-石墨烯的异质结构，并且能够把该研究推广到更加复杂的异质结构，例如金属-石墨烯-金属异质结构［16-18］。