Boost PFC带恒功率负载控制方法的研究

2021-08-30 07:06李刚李舒维邱伟

电气传动 2021年15期

李刚，李舒维，邱伟

（广西大学电气工程学院，广西南宁 530004）

在全球能源危机日益严峻的今天，新能源的发展越来越受到人们的重视，对于风力发电、光伏发电等的应用也愈加广泛。由于新能源发电等级的多样性，电能变换器有时需要通过级联方能满足实际需求[1-2]。当前级电能变换器与后级带有纯电阻负载并以闭环方式控制的变换器级联时，可将后级变换器视为前级变换器的恒功率负载（constant power load，CPL）[3]。典型的例子如利用闭环控制的Buck 稳压变换器接一个纯电阻负载，在其负载固定时该Buck变换器的输入功率为一个定值，即可视为一个恒功率负载。

利用新能源发电需要通过大量的电能变换器才能实现并网[4]。由于电能变换器大多为电力电子器件，因此在能量转换过程中的谐波问题是无法忽略的。Boost PFC 变换器是众多功率因数校正变换器中应用十分广泛的一种。Boost PFC变换器的控制方法经过多年的发展，已经由简单的电流内环及电压外环构成的双闭环PI 控制结构，发展到如今通过利用无桥拓扑[5-7]或者将微分平坦[8]、占空比预估算以及模糊控制[9-10]引入控制算法的设计方法等，以期达到良好的控制效果。而一种利用通过状态变换和状态反馈将一个非线性系统转化为线性系统，然后利用经典控制理论进行控制器的设计的方法也被大量利用，文献[11-12]都利用该控制方法获得了良好的控制效果，但是其应用场景较为简单，只能实现Boost PFC 带纯电阻负载的稳定运行。而由于在Boost PFC 变换器与Buck 变换器级联的情况下，Boost PFC 变换器的输出电流不连续，使得该方法在负载为恒功率负载时无法稳定运行。

为了解决这个问题，本文以Buck稳压变换器带一个纯电阻负载作为恒功率负载，利用输入输出线性化方法构造出一种适合恒功率负载的控制方法；并通过研究发现Boost PFC 变换器输出电压纹波与负载功率成一定比例关系，进而经过大量的数据测算得到能通过输出电压纹波的变化预测出负载功率的变化的计算关系；最后将预测所得到的负载功率代入控制方法，实现了Boost PFC 变换器在输入输出线性化方法下带恒功率负载恒压输出。在专业的电力电子仿真软件PSIM 中对所得到的控制方法进行了数字仿真实验，仿真实验结果表明该方法具有良好的动、静态特性，输入电流能精准跟踪输入电压，电流波形光滑；负载跳变时，动态响应快，输出稳定，表明该方法对负载具有良好的鲁棒性。

1 Boost PFC 变换器的输入输出线性化控制方法设计

1.1 Boost PFC变换器状态空间的建立

图1为Boost PFC变换器的拓扑结构。

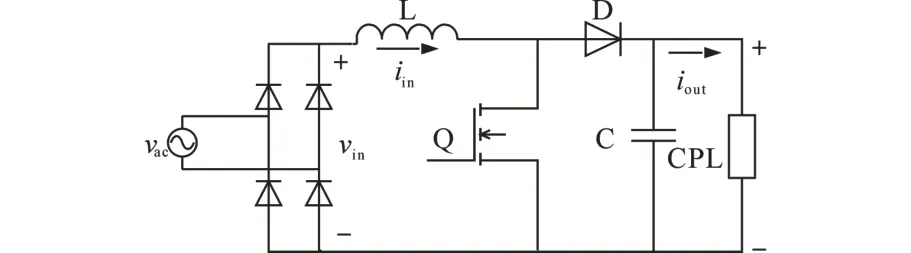
图1 Boost PFC变换器带恒功率负载的拓扑结构Fig.1 Topology structure of Boost PFC converter with a CPL

图1 中的恒功率负载（CPL）为一个闭环稳定工作的Buck 稳压变换器接一个纯电阻负载。对该Boost PFC 变换器用状态空间平均法进行建模，令vin=E（t），iin=iL，vo=uC，μ为MOS 管Q1的占空比。由于负载为非纯电阻电路，所以只能用iout来表示Boost PFC 变换器的输出电流，可以得到如下状态空间平均模型：

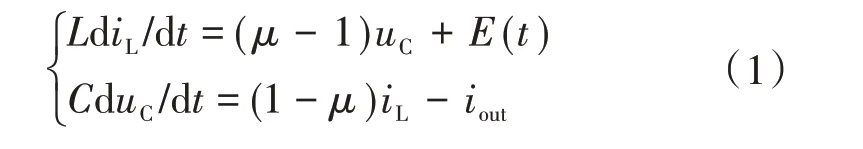
基于式（1）中的状态空间的平均模型，选取状态变量x=[x1x2]T=[iLuC]T，输入变量μ可设为MOS管Q1的占空比，输出变量可设为y=h（x），则可得到Boost PFC 变换器的单输入单输出仿射非线性系统的模型：

式（2）对应的单输入单输出的仿射非线性标准形式为

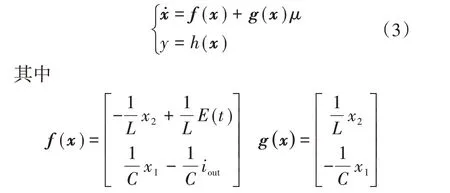
1.2 Boost PFC变换器输入输出线性化控制设计

根据文献[11]可知，当输出函数为h（x）=x1-iref时（iref为设定的电流参考值），可以得到如下的非线性坐标变换，可将原非线性系统转化为新坐标系下的线性系统：

式中：Φ-1(z)为求逆阵。

可以将式（3）的原非线性系统非精确线性化为一个准线性系统：

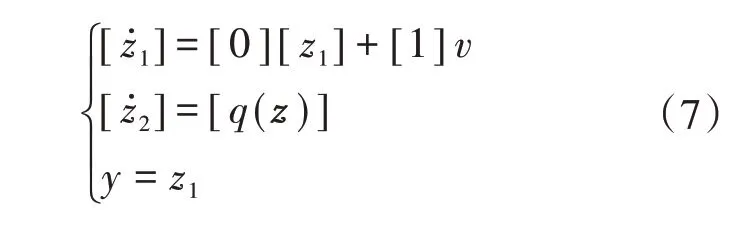
由式（7）得到新坐标系下控制律与原坐标系下控制律关系如下式所示：

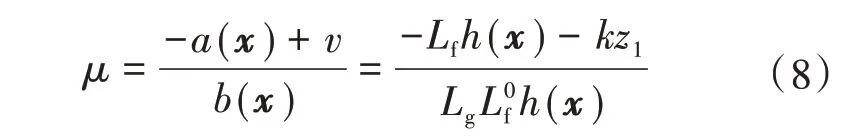
式中：k为e-kx的衰减系数，其值越大，误差衰减越快，k＞0。

根据能量守恒（忽略该系统中各种开关管及电感电阻等器件的功率损耗），再根据功率因数矫正后的效果就是Boost PFC 变换器的输入电流可以很好地跟踪输入电压，即输入电压与输入电流电位相同，设校正后的正弦输入电压峰值为Vm，输入电流的峰值为Im，期望的输出电压恒定为Uref，Iout为负载的输入电流，也就是Boost PFC 变换器的输出电流，则有下式成立：

鉴于Boost PFC 变换器在与Buck 变换器级联时其输出端直接与MOS 管Q2相连，在Q2断开时段无法得到连续的输出电流Iout，致使在负载发生扰动时式（12）的计算发生延迟甚至失效。解决的办法是将输出电流通过其他参量计算出来，可利用输出功率Pout和输出电压uout来表示输出电流：

实际中输出电压uout并不等于理想电压Uref，因为Boost PFC 变换器的输出电压带有纹波，并不是一个定值，采用uout计算占空比可以提高计算精度。

将式（12）代入式（11）可得：

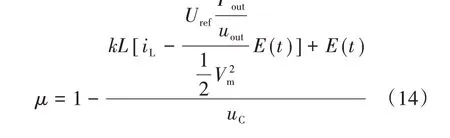
至此可以得出：当Pout的数值与负载功率一致时，便可以得到稳定的理想的输出电压以及PF值。

2 利用输出电压的纹波预测输出功率

2.1 稳定状态下输出电压纹波与负载功率的关系

在利用PSIM 仿真软件进行仿真研究时发现，在输入输出线性化方法下的Boost PFC 变换器稳定运行时，其输出电压的纹波大小Vpp跟负载功率Pout有关，且是线性相关的，图2 是以基准输出电压为230 V、负载功率分别为100 W，500 W，1 000 W 为例，利用PSIM 仿真软件得出的Boost PFC变换器输出电压的纹波图。

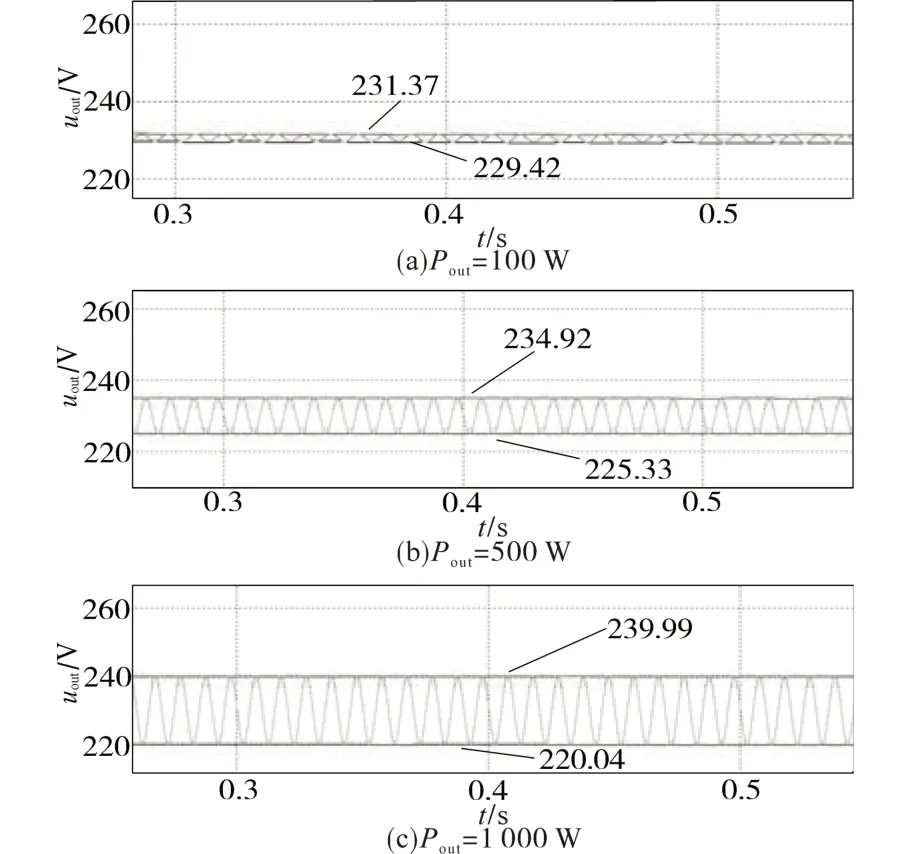
图2 基准输出电压为230 V，负载功率分别为100 W，500 W，1 000 W时输出电压的波形Fig.2 The output voltage waveforms when the reference output voltage is 230 V and the load power is 100 W，500 W and 1 000W respectively

由图2 可知，Boost PFC 变换器输出电压的纹波随着负载功率的增大而增大，分别为1.95 V，9.59 V，19.96 V。

在基准电压都是230 V 的情况下，从100 W到1 000 W，每隔25 W 测一组纹波大小，可得到如图3所示的散点图。

通过观察图3 可以发现，Boost PFC 变换器在稳定状态下运行时的输出电压纹波大小Vpp与负载功率Pout呈线性相关的关系。于是利用最小二乘法将图3中的数据拟合成一条直线：

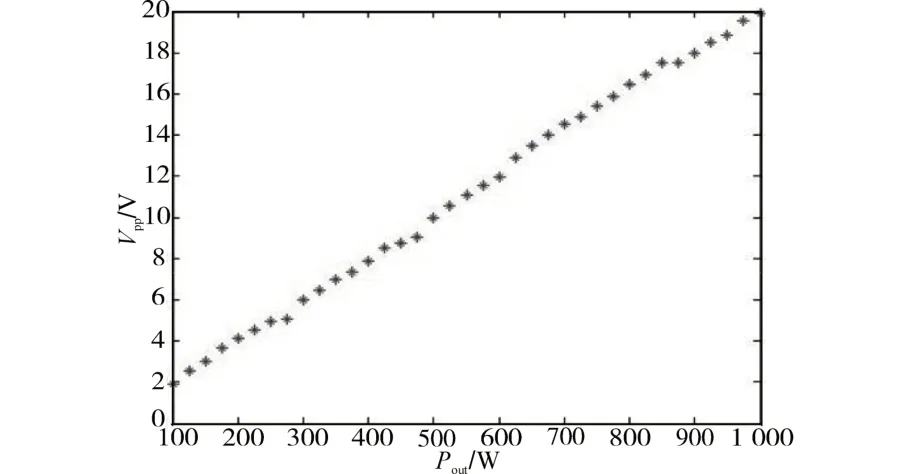
图3 输出电压纹波与负载功率的散点图Fig.3 Scatter diagram of output voltage ripple and load power

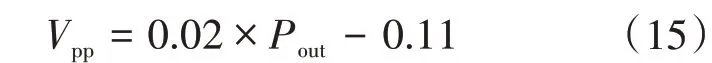
即

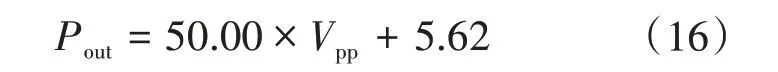
由此直线可以根据输出电压的纹波大小得到负载的功率。

2.2 功率跳变时输出电压纹波与负载功率的关系

根据上文中稳定时功率与输出电压纹波的关系可以推断，当负载功率发生跳变时，其变化的纹波可以用来推算跳变后的负载功率并对代入算法中的Pout进行校正。在经过仿真试验后发现，在跳变后第1 个周期的纹波（第1 个周期波峰与波谷的差的绝对值）会变大。以1 000 W跳变到500 W 为例，取在输出电压的波峰、波谷以及平衡点发生跳变时的输出电压纹波，如图4所示。

由图4 可知，跳变后的第1 周期内的纹波分别为42.46 V，32.61 V，42.21 V。可以看到，其跳变后第1个周期的纹波大小跟跳变时间有一定关系，这是稳定时电压的纹波与跳变时电压的变化叠加所导致的。而到了跳变后第3个周期的峰值分别为294.88 V，294.60 V，295.43 V，几乎没有差别，于是为了减小误差，并且尽量缩短计算时间，取跳变后第3个周期的波峰与跳变前的稳定纹波的波谷的差的平均值来对跳变后的功率进行校正，以尽量减少误差。

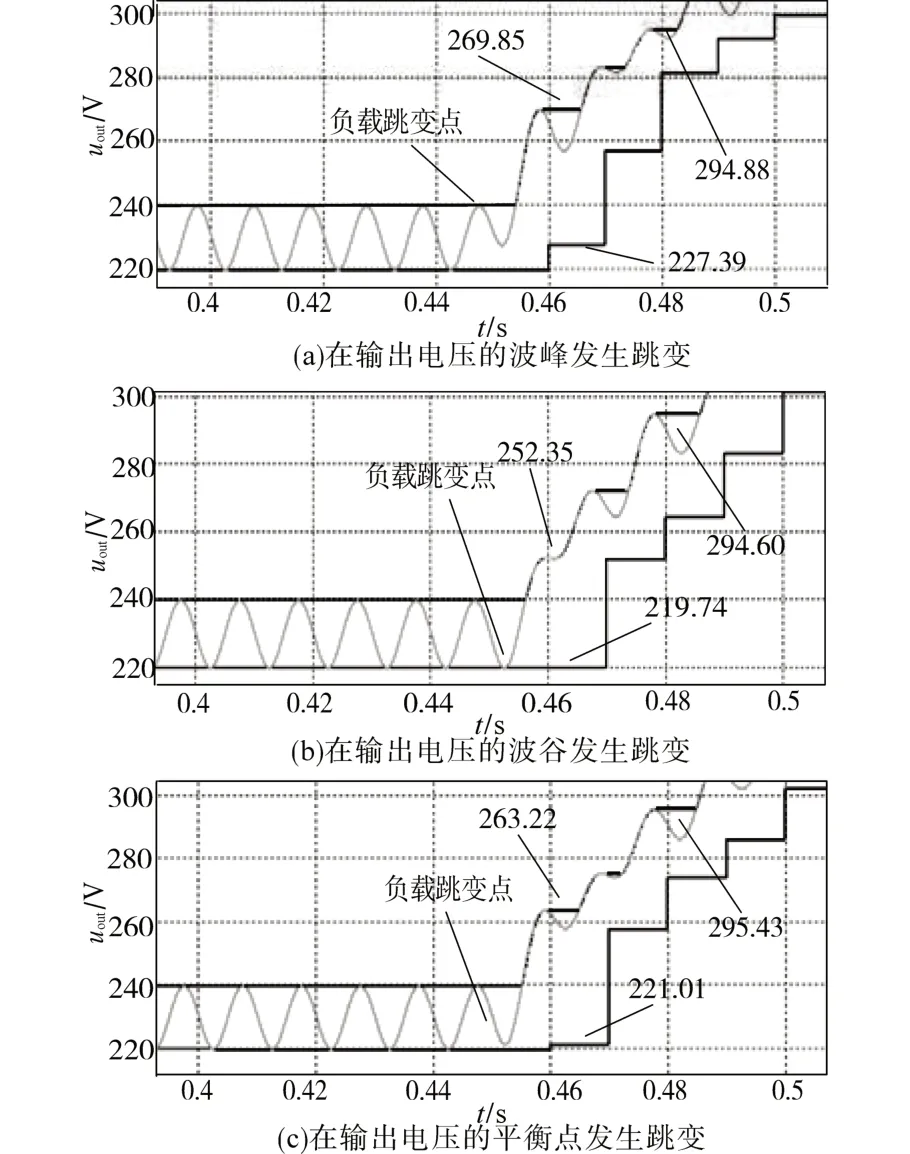
图4 负载功率跳变时输出电压纹波变化图Fig.4 Ripple change of output voltage during load power jump

同理，对于负载功率变大的情况，其输出电压会变小，取Vm为跳变后第3 个周期的波谷与跳变前稳定纹波波峰之差的平均值。

在基准电压是230 V的情况下，以500 W作为初始稳定功率为例，统计其Vm与跳变后的功率Pout，将得到的数据绘制成散点图，如图5和图6所示。

由图5 和图6 所示的结果可以发现，跳变后的功率Pout与Vm呈线性相关关系，因此可将Pout分别在增大和减小时与Vm的关系利用最小二乘法各拟合成一条直线：

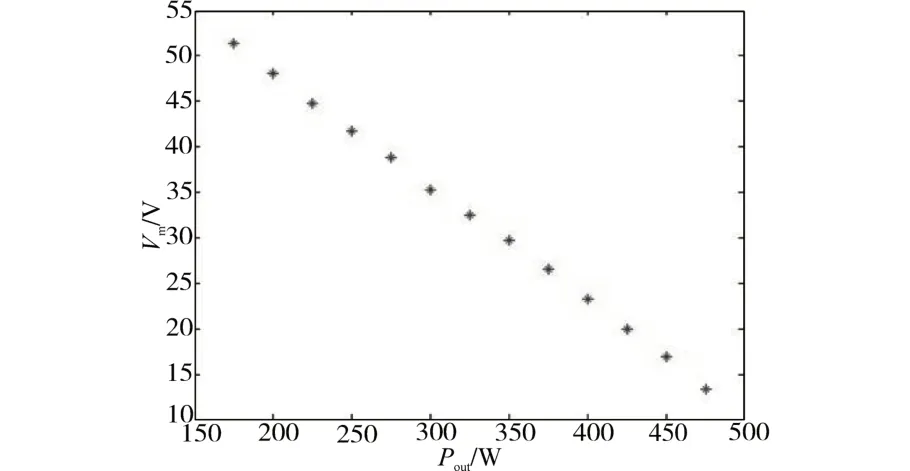
图5 跳变后功率下降时Pout与Vm的散点图Fig.5 Scatter diagram of Pout and Vm when power drops after jump

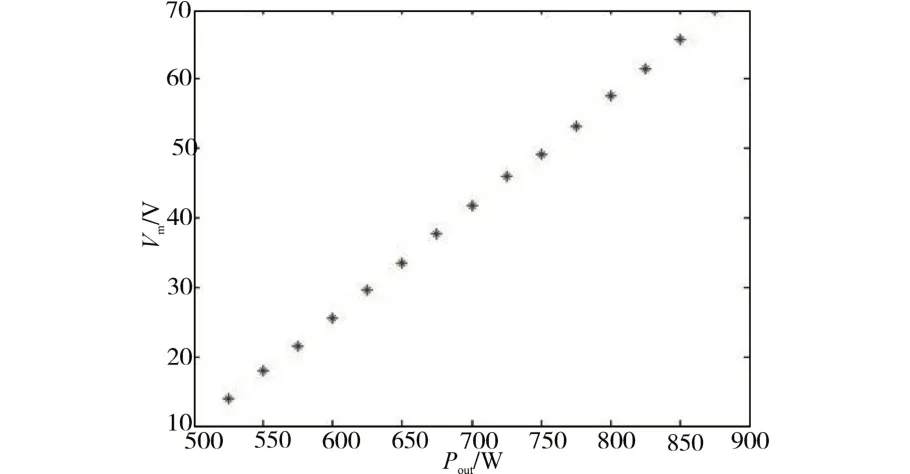
图6 跳变后功率上升时Pout与Vm的散点图Fig.6 Scatter diagram of Pout and Vm when power rises after jump

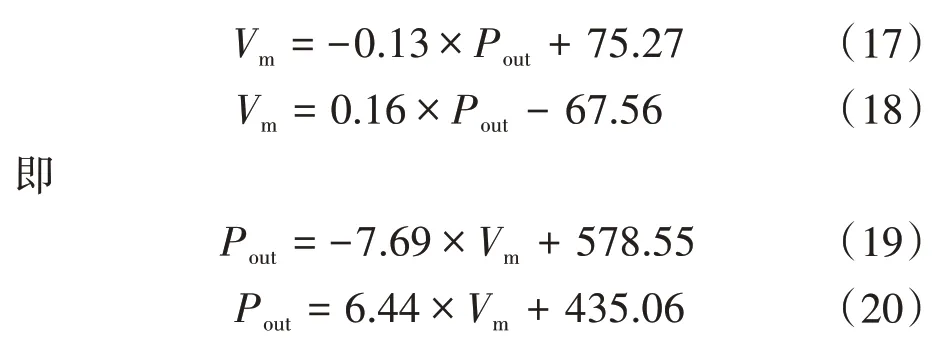
由式（19）和式（20）可以通过测量Vm的大小来计算出负载跳变后负载的功率即Boost PFC 转换器的输出功率，由此可以完成一次矫正。

通过测算可以得到初始稳定功率从100 W到1 000 W 的跳变后功率与Vm的拟合关系式并记录入表1。

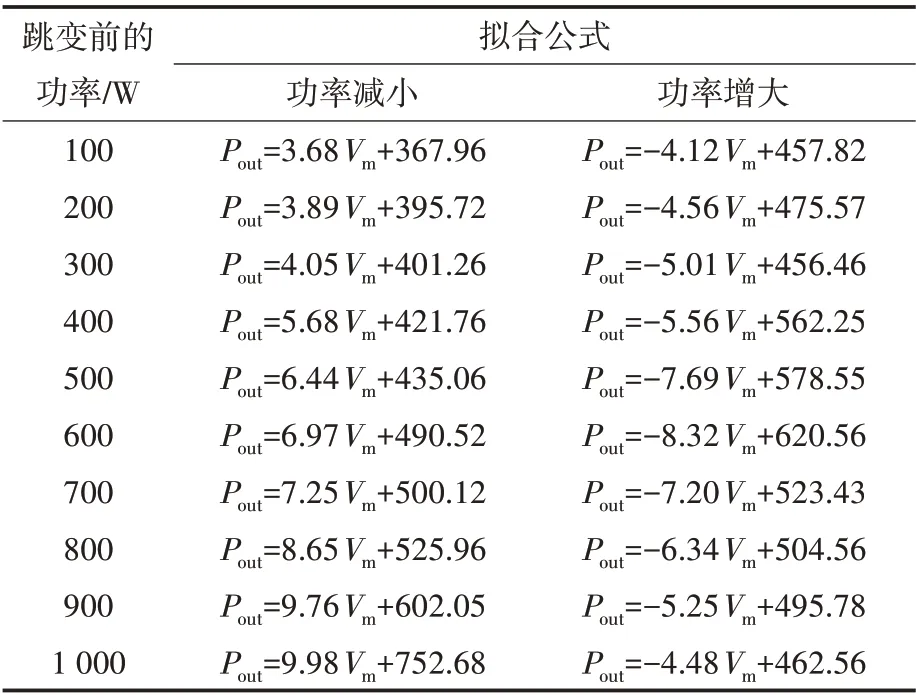
表1 不同初始功率的拟合公式Tab.1 Fitting formula of different initial power

2.3 二次矫正

在经过多组数据的测算后可以发现，在某些情况下时，利用上述的拟合公式计算出的Pout会与跳变后的实际功率有较大误差，会对输出电压造成影响，若计算出的Pout大于负载功率，输出电压uout的直流分量将高于Uref，反之则uout的直流分量会小于Uref。但是输出电压的误差不会影响到Boost PFC 输入端的输入电流跟踪输入电压（后面的仿真实验会加以验证）。这些误差的产生主要原因有两个：一是算不准，这是本身拟合曲线时的误差造成的；二是测不准，这是因为随着负载功率的变大，稳定时输出电压的纹波也会变大，使得在相同初始稳态功率的情况下，不同的跳变时刻会对Vm的数值产生较大影响，进而影响到代入拟合公式后计算出的Pout。因此误差往往会出现在大范围的功率跳变和初始稳定功率较大的情况下，但是根据实际测算可知，100 W到1 000 W 之内的跳变，其误差不会超过100 W。于是对于某些对输出电压要求不高的应用场景（例如光伏发电），一次矫正就可以满足实际需要，而在某些对输出电压要求高的场景，则需引入二次矫正。

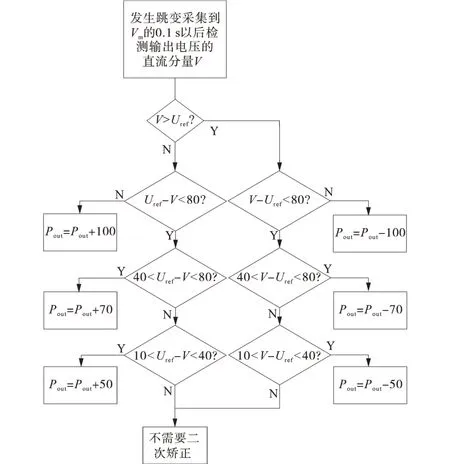
图7 二次矫正的流程图Fig.7 Flow chart of secondary correction

至此，可以得到当负载发生跳变时，根据输出电压纹波的变化预测输出功率的步骤如图8所示。

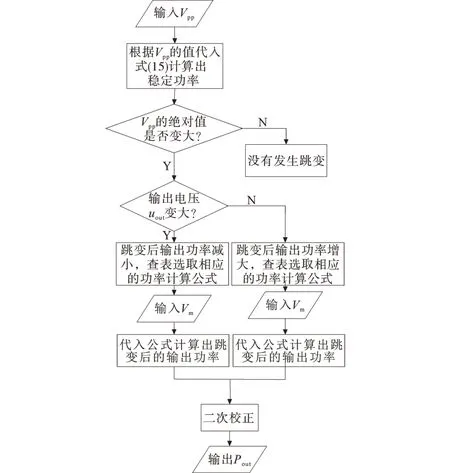
图8 根据纹波调整Pout流程图Fig.8 Flow chart of Pout adjustment according to ripple

将通过该步骤预测得到的负载功率Pout代入式（14），便可使Boost PFC 变换器在带恒功率负载的情形下稳定运行。

3 数字仿真实验验证

3.1 数字仿真实验参数

系统仿真采用专业的电力电子仿真软件PSIM进行数字仿真实验，仿真系统的设计图如图9所示。

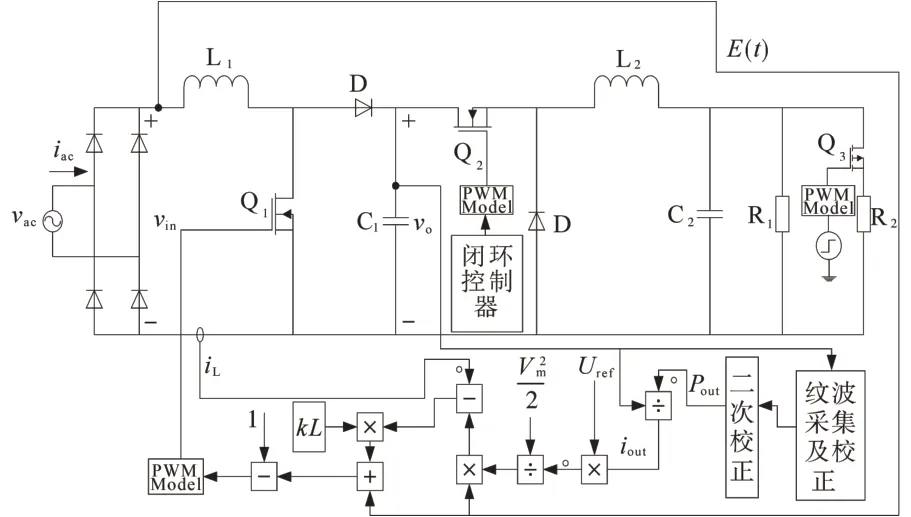
图9 Boost PFC带恒功率负载输入输出线性化方案图Fig.9 Scheme of input and output linearization of Boost PFC with constant power load

图9 中，输入电压vac=150sin（ωt）；Boost PFC变换器的期望输出电压Uref=230 V；MOS 管Q1的频率f1=80 kHz；MOS 管Q2的频率f2=20 kHz；电感L1=3 mH；电感L2=5 mH；电容C1=700 μF；电容C2=1 000 μF；k=30。与Boost 电路级联的Buck 电路采用电压单闭环控制，再接入一个纯电阻负载可视为一个恒功率负载，通过控制接入Buck 电路的纯电阻负载的阻值控制该恒功率负载功率的大小。MOS 管Q3接一个脉冲信号的作用是控制负载功率的跳变，当电阻R1并联一个电阻R2时，负载的功率会提升，当电阻R1和R2并联时，断开R2支路，负载功率会下降，据此可以控制跳变时间以及跳变前后的负载功率。例如：当电阻R1=5 Ω 时，该恒功率负载的功率为500 W，当电阻R1=5 Ω，电阻R2=5 Ω 时，Q3由关断到接通时，该恒功率负载的功率由500 W 跳变到1 000 W；当电阻R1=10 Ω，电阻R2=10 Ω 时，Q3由接通到关断，该恒功率负载的功率由500 W 跳变到250 W。

3.2 基准输出电压为230 V 负载功率为500 W的稳态仿真

负载功率不变时的稳态运行是为了观察该算法在带恒功率负载时是否能稳定运行、启动调节时间以及输出电压在启动时是否有超调。图10 为该算法下Boost PFC 变换器带恒功率负载的输入电压、输入电流以及输出电压。

图10 Boost PFC变换器带恒功率负载的输入电压、输入电流与输出电压的启动波形Fig.10 Input voltage，input current and output voltage waveforms of Boost PFC converter with CPL

从图10 可知，启动调节时间仅为5 ms，此后输入电流精准跟踪输入电压，输出电压也能稳定在230 V，并且整个调节过程几乎没有超调。

3.3 基准电压为230 V负载功率增大时的仿真

图11、图12 所示为功率跳变跨度很大时Boost PFC 变换器的输出电压，当发生突变后的第3 个周期的输出电压的峰值为193.63 V，则Vm=94.87 V，代入拟合公式可得跳变后的功率Pout=1 045.90 W，经过二次矫正，Pout=995.90 W。

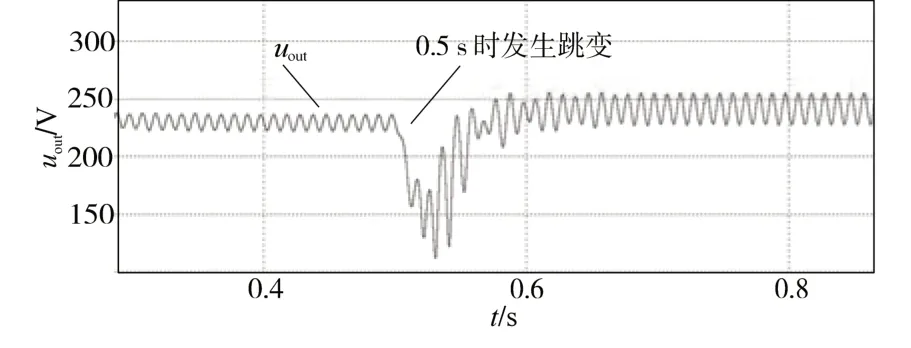
图11 负载从500 W跳变到1 000 W时输出电压波形（无二次矫正）Fig.11 The output voltage waveform of load from 500 Wto 1 000 W（without secondary correction）

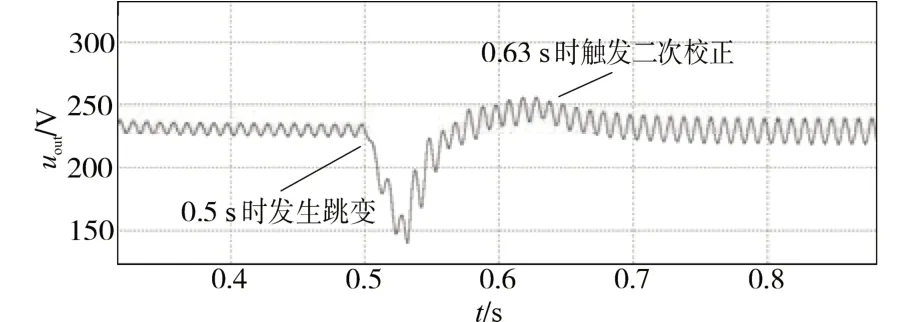
图12 负载从500 W跳变到1 000 W时输出电压波形（有二次矫正）Fig.12 The output voltage waveform of load from 500 W to 1 000 W（with secondary correction）

由图11、图12 可知，输出电压在经过短暂调整后，在未经过二次矫正时的直流分量明显高于经过二次矫正后的直流分量。

图13、图14 为负载跳变时，输入电压、电流波形（无/有二次矫正）。根据图13、图14 所示的结果可以看到，负载突变不影响输入电压，输入电流在负载跳变时变化平滑，几乎没有过渡过程。并且是否加入二次矫正并不影响输入电流跟踪输入电压。

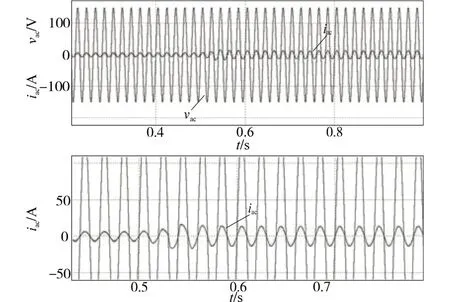
图13 负载从500 W跳变到1 000 W时输入电压和输入电流波形（无二次矫正）Fig.13 Input voltage and input current waveforms of load from 500 W to 1 000 W（without secondary correction）

图14 负载从500 W跳变到1 000 W时输入电压和输入电流波形（有二次矫正）Fig.14 Input voltage and input current waveforms of load from 500 W to 1 000 W（with secondary correction）

图15 所示为功率跳变跨度很小时Boost PFC变换器的输出电压，发生突变后第3个周期输出电压的峰值为228.07 V，则Vm=6.44 V，代入式（19）可得跳变后的功率Pout=590.04 W。图16为功率跳变跨度很小时Boost PFC变换器的输入电压、电流波形。由图16可知，在跳变前、后输入电流都能很好地跟踪输入电压，并且电流变化平滑。

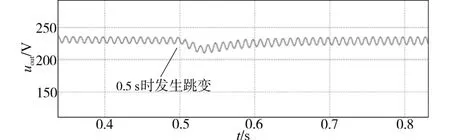
图15 负载从500 W跳变到590 W时输出电压波形Fig.15 The output voltage waveform of load from 500 W to 590 W

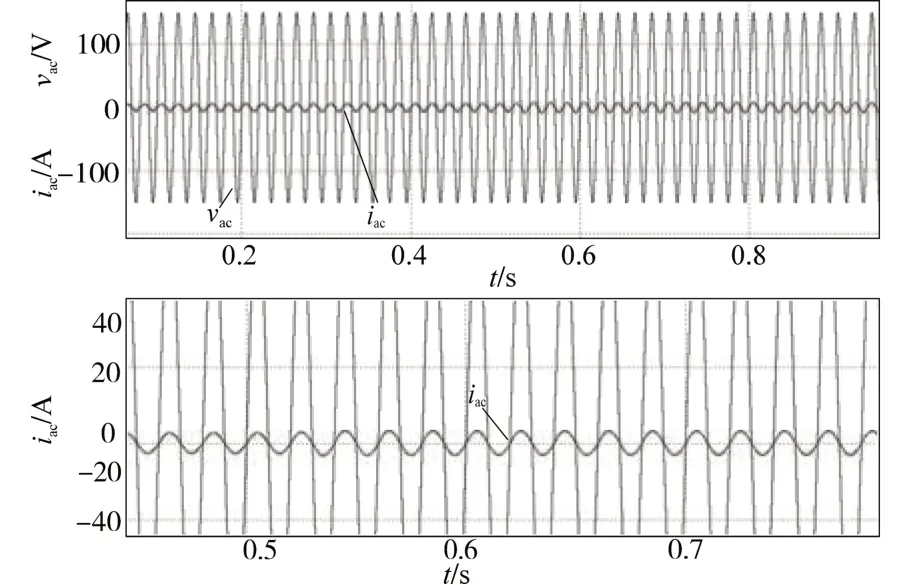
图16 负载从500 W跳变到590 W时输入电压和输入电流波形Fig.16 Input voltage and input current waveforms of load from 500 W to 590 W

3.4 基准电压为230 V负载功率减小时的仿真

图17 所示为功率跳变跨度很大时的Boost PFC 变换器的输出电压，发生突变后的第3 个周期的输出电压的峰值为268.03 V，则Vm=43.36 V，代入式（19）可得跳变后的功率Pout=245.28 W。

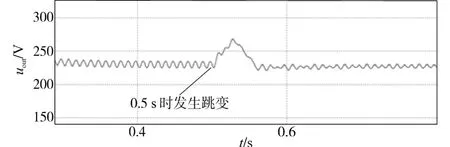
图17 负载从500 W跳变到250 W时输出电压波形Fig.17 The output voltage waveform of load from 500 W to 250 W

图18 所示为功率跳变跨度很小时Boost PFC变换器的输出电压，发生突变后的第3 个周期的输出电压的峰值为246.84 V，则Vm=22.16 V，代入式（19）可得跳变后的功率Pout=408.21 W。

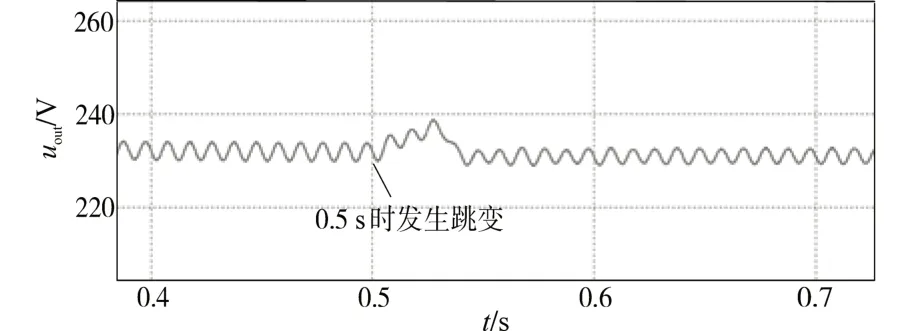
图18 负载从500 W跳变到410 W时输出电压波形Fig.18 The output voltage waveform of load from 500 W to 410 W

由图17、图18 所示的结果可知，输出电压在经过短暂调整后，除了纹波有相应的变化外，其直流分量几乎不变，在0.63 s 时没有触发二次矫正。

图19、图20 所示为Boost PFC 变换器在负载跳变前后整流前的输入电压与电流，可以看到，负载突变不影响输入电流跟踪输入电压，输入电流在负载跳变时变化平滑，几乎没有过渡过程。

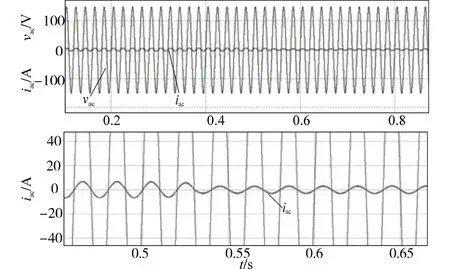
图19 负载从500 W跳变到250 W时输入电压和输入电流波形Fig.19 Input voltage and input current waveforms of load from 500 W to 250 W

由上述仿真结果可知，该算法在多种负载跳变的情况下都有良好的表现。

4 结论

本文实现了利用Boost PFC 输出电压的纹波对负载功率的变化进行预测，利用经过输入输出线性化方法得到的控制方法来实现负载为恒功率负载的稳定运行。PSIM软件仿真表明：该方法启动入稳时间快，在带恒功率负载时几乎无超调，稳态时能够保持输入电流对于输入电压的精准跟踪，输出电压亦保持恒定。在负载跳变的情况下依然可以稳定运行，输出电压能在经过短暂的调整后稳定在理想电压值，电流变化响应迅速，电流波形光滑，能一直保持稳定运行，显示出所提供的方法具有良好静态性能与迅速的动态响应，以及对负载扰动的强鲁棒性。