一种牵引供电系统负载电压谐波抑制策略

王丽丽

（长治职业技术学院机械电子工程系，山西长治 046000）

目前，铁路牵引供电系统多采用异相供电方式[1]，由于牵引供电系统中存在大量非线性、不平衡负载，该异相牵引供电方式会造成较为严重的电能质量问题，如负载电压中出现较高的谐波，以及出现严重的三相不对称等[2-4]。如若不对负载中的电能质量问题进行有效处理，畸变和不对称的电压势必会影响牵引供电系统中运行设备的可靠运行，也会影响到负荷的安全运行。考虑到牵引供电系统高电压、大容量的供电需求，本文将电力电子变压器（power electronics transformer，PET）引入到牵引供电系统中[5]，利用PET 来对牵引供电系统中的电能质量问题进行治理。

PET技术将电力电子变流技术与高频变压技术结合起来，可以灵活地控制电压幅值和相位，从而达到提高电能质量的目的[6-7]，因此应用于牵引供电系统的PET 研究受到了学者的广泛关注[8-10]。但是，面向牵引供电系统的PET电能质量治理技术还未得到深入研究。

近年来，针对PET 的研究多集中在将其作为微电网与大电网的接口，即能量路由器来使用，以实现能量在微电网与大电网之间的双向流动[11-12]。但鲜有相关文献针对PET 输出的电能质量问题展开研究，未挖掘出PET 的电能质量治理能力。本文以输出级模块化并联的PET 为研究对象，具体探讨PET 的电能质量治理能力，充分挖掘出其电能质量调节方法[13]。

目前，已有相关文献单独针对逆变器并联的系统进行电能质量调节。文献[14-15]提出将含有各次谐波的逆变器输出电压在对应的d-q旋转坐标系下变换成直流量并滤波，送入到PI 控制器，在实现输出电压跟踪基波参考电压的同时滤除掉输出电压中各次谐波成分，但文献中所提控制策略对3k次谐波不适用。为能有效抑制3k次谐波，文献[16-17]通过在逆变器谐波补偿环节中采用多谐振比例控制器，能有效抑制输出电压中的谐波成分，但多谐振控制的增益取太大时会造成控制系统不稳定。文献[18]提出通过添加虚拟谐波阻抗的方式，将逆变器输出谐波阻抗抵消掉，降低了输出电压的畸变率（total harmonics distortion，THD），但文献中虚拟谐波阻抗的选取较为繁琐。文献[19-22]采用下垂控制来降低逆变器输出电压THD，通过并联的逆变器来分担谐波电流以达到降低输出电压THD 的目的，但文献中下垂控制方程的选取需要依赖于逆变器输出阻抗类型。

本文在上述文献的基础上，针对牵引供电系统负载电压谐波问题，首先分析了非线性负荷造成PET 输出端电压畸变的机理，然后对已有的主从控制策略进行了改进，将电能质量治理功能嵌入到PET 输出侧从逆变器中，充分利用从逆变器剩余可用容量对负载电压谐波进行抑制，最后基于PSCAD 仿真和实验对本文所提控制算法的有效性进行了验证。

1 PET拓扑结构和原理

图1 为本文所采用的PET 整体拓扑，其主要由高压输入级级联AC-DC 整流环节、中间级DC-DC 隔离环节、低压输出级DC-AC 逆变环节3 部分组成。

图1 PET整体拓扑结构Fig.1 The overall structure of power electronic transformer

本文主要研究的是PET 输出侧的电压质量问题，因此重点对输出侧的电压质量改善策略进行分析，对于输入级和中间级的控制策略，本文不再阐述。

2 PET输出侧电压畸变原因分析

对于PET，其输出侧一般采用主从控制，其中一个逆变器充当电压源角色，称为主逆变器，主要用来维持输出侧电压的稳定，同时给其它逆变器提供电压基准；而其余逆变器则充当电流源角色，根据接收的电流指令来控制其输出功率。采用主从控制的PET 输出侧控制框图如图2 所示。

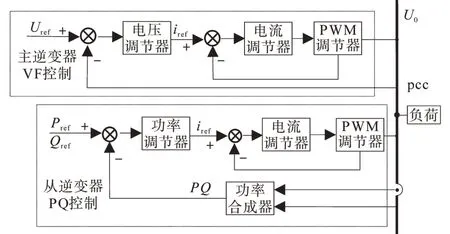
图2 主从控制原理图Fig.2 Master-slave control block diagram

图3 为主逆变器控制框图，是主从控制中主逆变器比较经典的控制算法，包括电压外环和电流内环。电压外环负责维持逆变器输出端电压稳定，电流内环能提高系统响应速度。

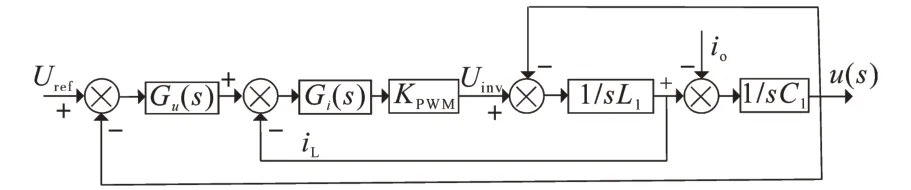
图3 主逆变器控制框图Fig.3 The control block diagram of main inverter

图3 中，Uref为主逆变器参考电压指令；Gu（s）为电压外环传递函数，可以是PI 控制或者P 控制；Gi（s）为电流内环传递函数，同理也可以采用PI 控制或者P 控制。根据图3 可以得出PET主逆变器输出电压和电流的关系表达式如下式：

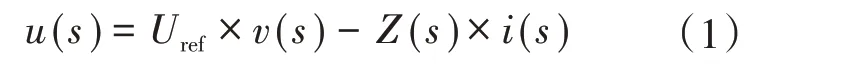
其中

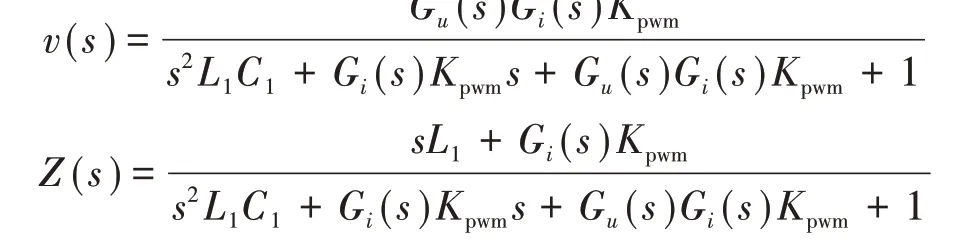
式中：i（s），Uref分别为主逆变器输出的实际电流及给定的参考电压指令；u（s）为主逆变器实际输出电压；v（s）为主逆变器u（s）到Uref间的传递函数；Z（s）为主逆变器Uref置0 时，主逆变器u（s）与输出电流i（s）的比值，即等效输出阻抗；Kpwm为逆变器的等效增益；L1，C1分别为逆变器的滤波电感和滤波电容。

当PET 输出侧带非线性负荷运行时，若不进行任何电能质量调节，则电流i中将含有大量谐波成分，根据叠加定理，式（1）可以表示为

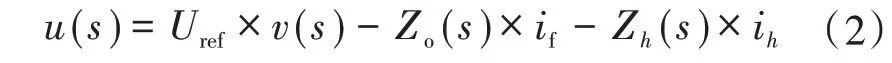
式中：Zo（s），Zh（s）分别为主逆变器的等效基波阻抗和谐波阻抗，表达式与式（1）中Z（s）相同。

当主逆变器带非线性负载运行时，主逆变器输出电流中将存在各次谐波电流分量，由式（2）可知，流过主逆变器上的各次谐波电流分量将在其输出谐波阻抗Zh（s）上产生相对应的谐波压降。由于给定的参考电压Uref是纯正弦量，因此主逆变器上产生的谐波压降将会出现在其输出电压u（s）中，进而导致u（s）畸变。如若减少流入主逆变器的谐波电流分量，相当于减少了谐波电流在逆变器Zh（s）上的谐波压降，则u（s）畸变率将大大降低。

3 PET输出侧电压谐波抑制策略

3.1 PET输出侧电压谐波抑制策略分析

本文所提出的电压谐波抑制策略中，主逆变器维持原有的控制策略，依然充当电压源角色，而从逆变器充当电流源角色，仅将电能质量功能嵌入到从逆变器中，增加了从逆变器电能质量治理功能，即由从逆变器来承担负载电流中的负序分量。其输出侧等效电路图如图4所示。

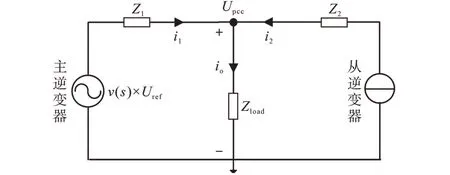
图4 具有电能质量治理功能的主从逆变器等效电路图Fig.4 The equivalent circuit diagram of master-slave inverter with power quality control function

图4 中，Upcc为主逆变器输出端电压，将负载电流io进行分解得到基波电流if和谐波电流ih如下式所示：

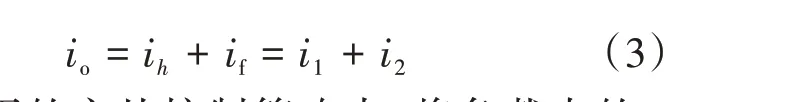
本文采用的主从控制策略中，将负载中的ih全部由从逆变器来提供，负载中的if则由主、从逆变器共同分担，如下所示：

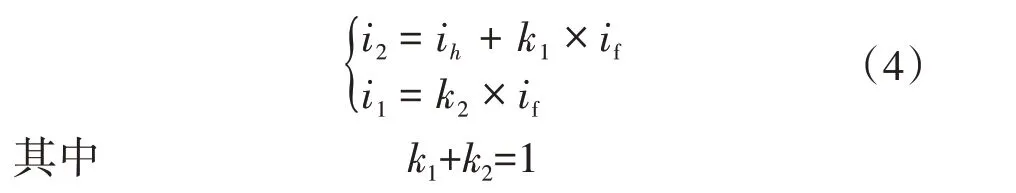
采用本文的控制策略后，主逆变器输出电流i1中含有的ih分量近似为零，如下式所示：

则主逆变器输出电压的THD经计算得：

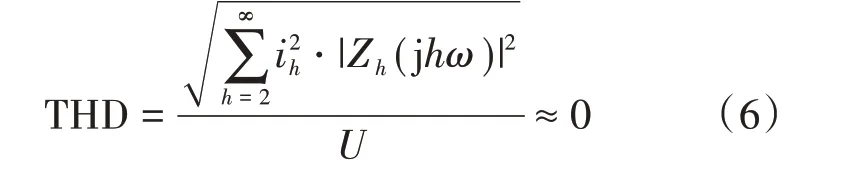
式中：Zh为逆变器的谐波阻抗；ω为逆变器角频率；U为逆变器输出电压基波幅值。

由式（6）可知，当从逆变器提供负载中的全部ih时，主逆变器输出电压的THD 为0，输出电压中的电压谐波成分得到有效抑制。而实际中由于电流采样误差的原因，输出电压中的谐波成分不能完全得到抑制。

3.2 主从控制策略

PET输出侧主逆变器维持原有的控制策略不变，采用恒压恒频控制来维持输出电压稳定，具体控制框图见图3。而从逆变器采用恒功率控制，可等效为电流源，并在从逆变器控制环中增加谐波电流控制环，图5 为本文所提出的从逆变器控制策略框图。

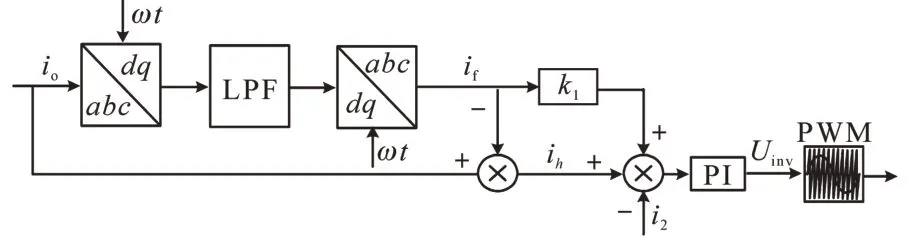
图5 从逆变器控制原理图Fig.5 The control block diagram of slave inverter

图5 中，io为负载电流，if为负载中的基波电流，ih为负载中的谐波电流。谐波提取具体实现过程为：将采样得到的负载电流io经过基波abc/dq旋转坐标系下进行变换后送入到低通滤波器，然后经过基波dq/abc反变换后得到负载中的基波电流if，用io减去基波电流if就得到了负载中的谐波电流ih。具体坐标变换过程如下：

式中：Iof为基波电流的有效值；Ih为各次谐波的谐波电流有效值；θ1，θh分别为基波初始相位和各次谐波初相位；h为谐波次数；k为用来计算谐波次数的数字。

由图5 可知，从逆变器补偿谐波电流的核心思路在于分离出负载电流中的基波和谐波电流分量。具体方法如下：将负载电流io通过基波旋转坐标变换后，基波电流分量转换为直流分量，而谐波分量则转换为6k次谐波，通过低通滤波器LPF滤波后，其中的谐波都被低通滤波器滤除掉，剩下的直流量就是基波分量在基波旋转坐标变换后得到的值，再将其经过基波旋转坐标逆变换即可得到负载电流中的基波电流分量if，用负载电流减去基波分量即得到了负载电流中的谐波电流分量ih，即负载中的谐波电流与基波电流被分离出来。基波旋转坐标逆变换T（θ）dq0/abc的表达式如下所示：

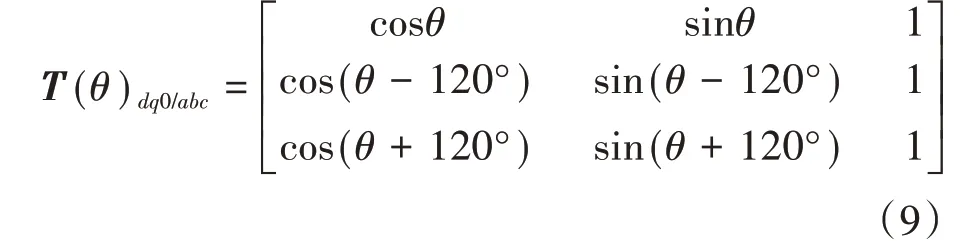
从逆变器的参考电流指令值选取如下：将负载电流中的基波电流分量if乘以一比例系数k1后与负载电流中的谐波电流ih叠加后作为从逆变器的参考指令值，并与从逆变器实际输出电流i2相比较，将所得到的差值送入到PI控制器得到调制波，与载波比较后产生PWM波去驱动相应的开关管。

4 仿真分析

为了证明本文所提出的电压谐波抑制策略的可行性，在PSCAD 仿真环境中搭建如图1 所示的仿真模型。仿真主要参数为：PET 高压侧电压10 kV，PET 直流侧电压750 V，PET 输出侧电压380 V，主逆变器电压环PI 积分系数0.5，主逆变器电流环PI 比例系数45，从逆变器功率环PI 积分系数1.4，从逆变器功率环PI比例系数20，从逆变器电流环PI 比例系数75，从逆变器电流环PI积分系数0.08。

本文中用直流侧带电阻的三相不可控整流桥和纯电阻负荷并联来模拟PET 带非线性负载运行这一工况。

图6为PET输出侧未加谐波抑制功能的输出波形。

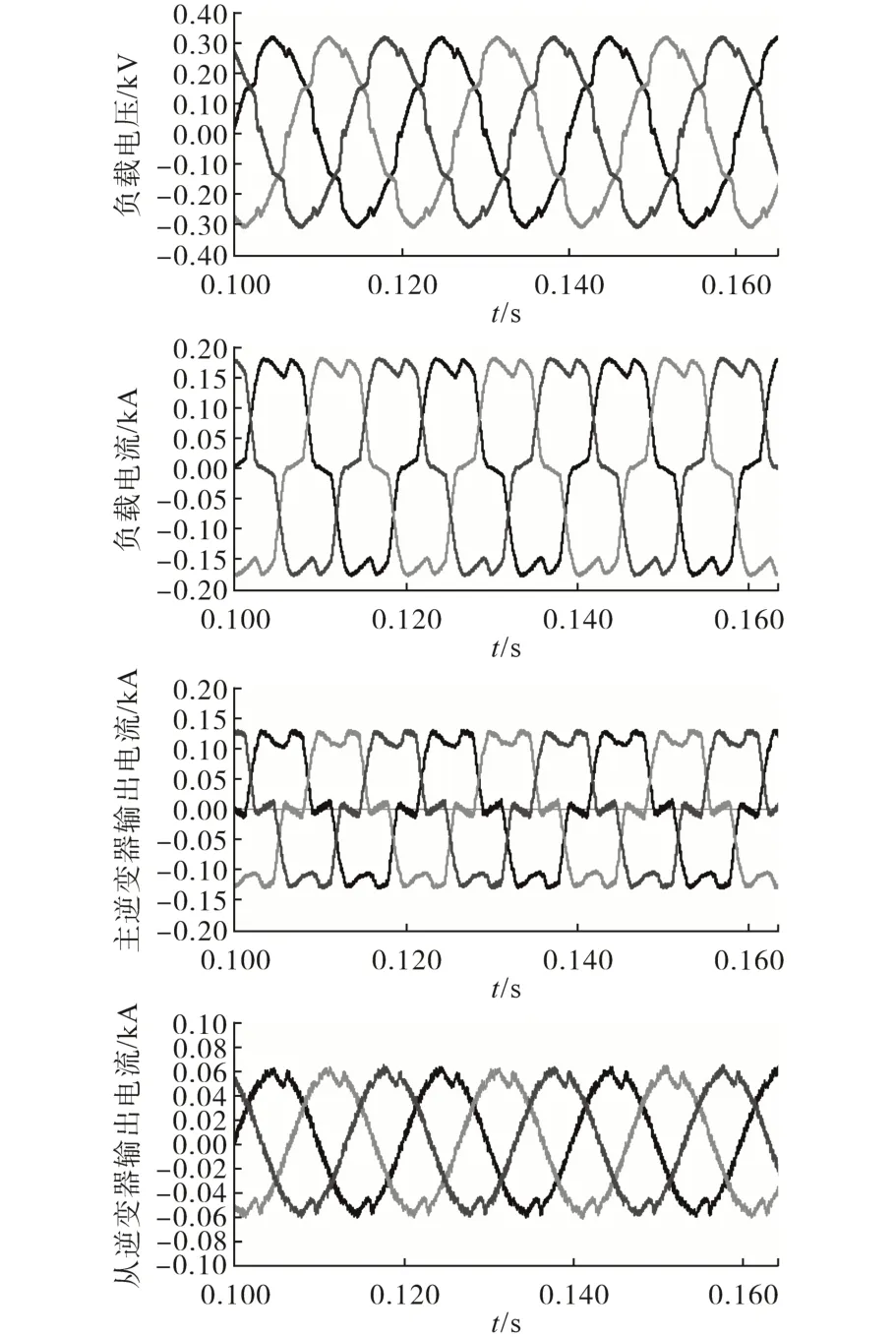
图6 从逆变器未加谐波电流补偿的仿真结果Fig.6 The simulation results without harmonic current compensation from slave inverter

从图6的仿真结果可以看出，从逆变器未采取谐波电流补偿时，负载电压中含有大量各次谐波电压，进而导致负载电压波形出现严重畸变。表1为经过计算得出的负载电压中的各次谐波畸变率。

表1 负载电压中的各次谐波畸变率（未加谐波抑制）Tab.1 Harmonic distortion rate of different frequency in load voltage without harmonic suppression

基于前文的理论分析可知，若不对逆变器控制算法加以改进，其输出电压中含有大量各次谐波电压成分，从表1可以看出，此时的负载电压畸变率达到10%左右，会影响到负荷乃至设备的安全稳定运行。

图7 为PET 输出侧加谐波抑制功能的输出波形。

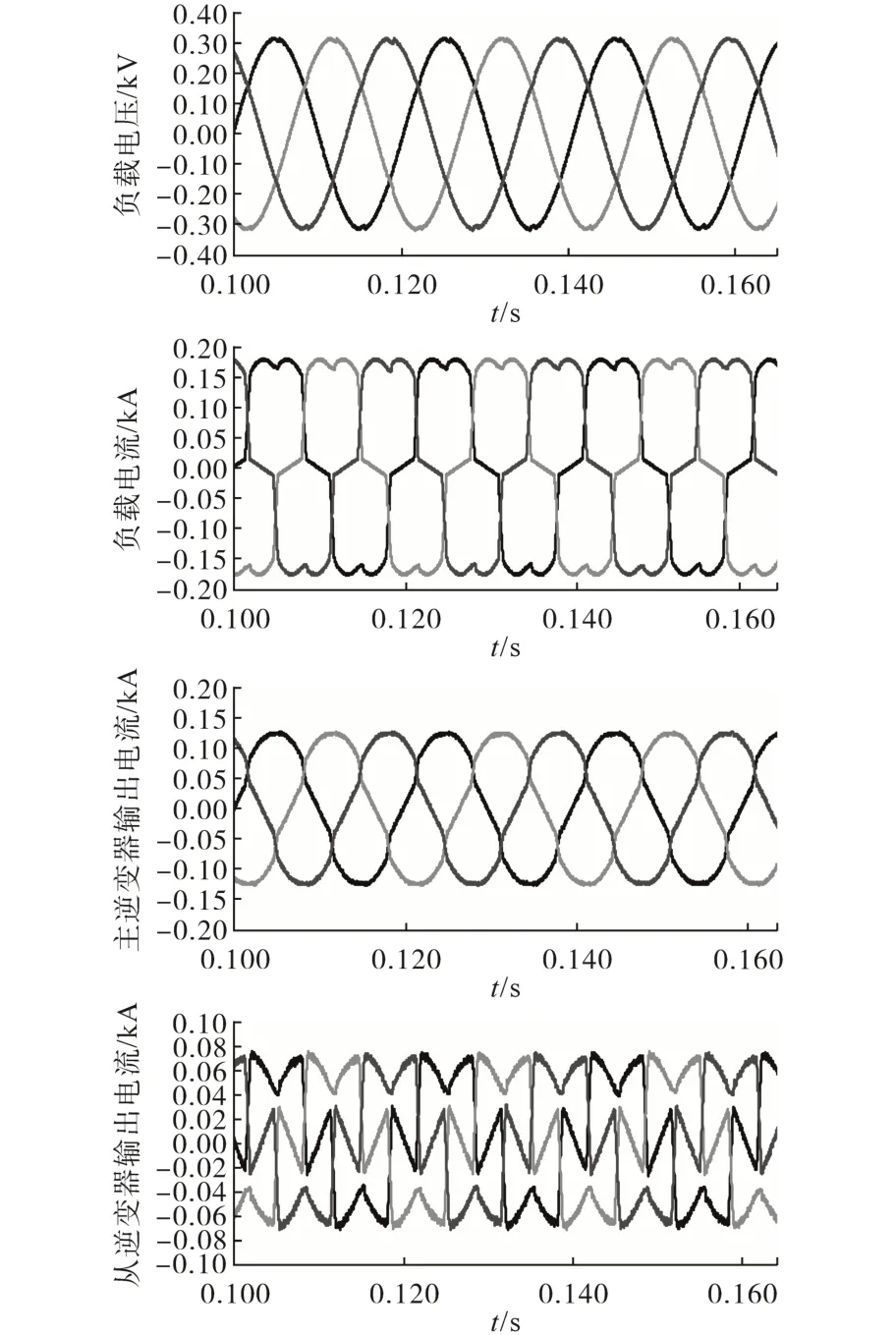
图7 从逆变器进行谐波电流补偿的仿真结果Fig.7 The simulation results of harmonic current compensation from slave inverter

从图7 的仿真结果可以看出，将谐波电流补偿环嵌入到从逆变器控制算法中后，从逆变器提供了负载中的大部分谐波电流，而流入到主逆变器中的谐波电流分量很小，因而负载电压中的谐波含量大大降低，负载电压基本正弦，这与前面的理论分析相符合。表2为经过计算得出的负载电压中的各次谐波畸变率。

表2 负载电压各次谐波畸变率（加谐波抑制）Tab.2 Harmonic distortion rate of different frequency in load voltage with harmonic suppression

以上仿真结果表明，将谐波电流补偿环嵌入到从逆变器控制算法中后，负载电压中的谐波含量明显降低，其总的谐波畸变率为0.69%。

5 实验验证

为了验证所提的电压谐波抑制算法的可行性、有效性，本文搭建了实验室样机，样机控制器采用TI公司的TMS28335芯片，实验参数取值与仿真参数一致，通过编程实现所提控制算法，实验工况分2 种，以此进行对比，实验波形如图8和图9所示。

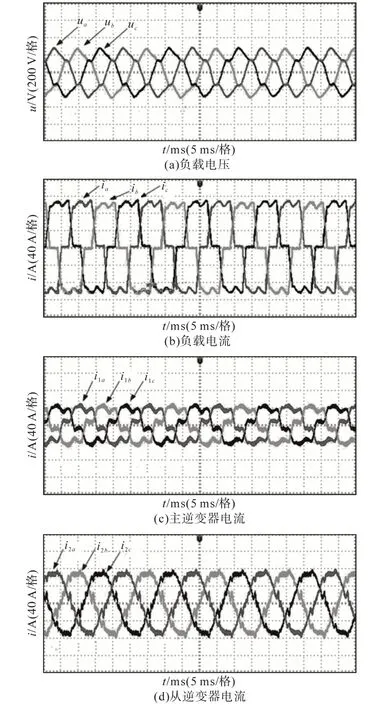
图8 从逆变器不进行谐波电流补偿的实验结果Fig.8 The experimental results without harmonic current compensation from slave inverter

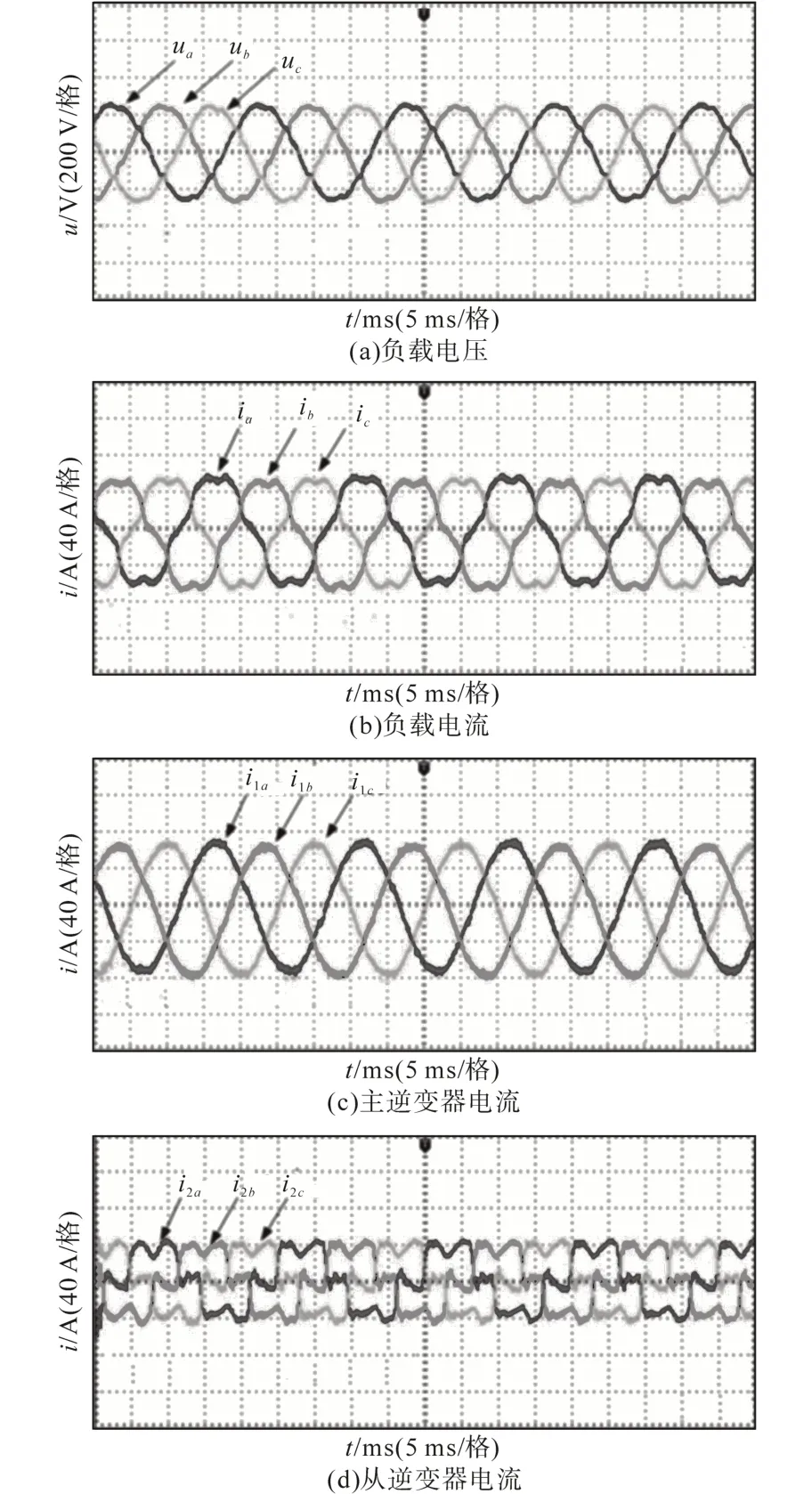
图9 从逆变器进行谐波电流补偿的实验结果Fig.9 The experimental results with harmonic current compensation from slave inverter

当逆变器带非线性负载运行且不进行谐波电流补偿时，图8a～图8d分别对应的是负载电压、负载电流、主逆变器电流、从逆变器电流波形。从图8a 的实验结果可以看出，当从逆变器不采取谐波电流补偿时，负载电压中的谐波含量较大，负载电压畸变严重。这是因为当逆变器带非线性负载运行时，负载电流中将含有大量谐波电流，如图8b所示，负载电流畸变严重。此时负载电流中的谐波电流将分别流入到主、从逆变器中，导致主、从逆变器输出电流畸变，如图8c和图8d所示。由于负载中的谐波电流流入到了主逆变器中，谐波电流将在主逆变器的输出阻抗上产生谐波压降，进而导致主逆变器输出电压畸变，这与前文的理论分析相符合，从图8a 中的负载电压波形可以看出，此时的负载电压含有大量谐波。

当逆变器带非线性负载运行并进行谐波电流补偿时，图9a～图9d 分别对应的是负载电压、负载电流、主逆变器电流、从逆变器电流波形。与图8 不同的是，此时在从逆变器控制环中增加了谐波电流补偿环。从图9a 的实验结果可以看出，当从逆变器控制环中增加了谐波电流补偿环后，负载电压中的谐波含量大大降低，负载电压基本正弦。这是因为此时负载电流中的全部谐波电流分量都由从逆变器来提供，因此从逆变器输出电流严重畸变，如图9d 所示，而主逆变器此时只提供负载电流中的基波电流，因而主逆变器的输出电流基本正弦，如图9c所示。由于负载中的谐波电流都流入到了从逆变器中，因而主逆变器输出电压基本正弦，这与前文的理论分析相符合，从图9a 中的负载电压波形可以看出，此时的负载电压谐波含量大大降低。

由图8 和图9 的实验结果，经过对比分析进一步验证了本文所提策略的有效性。将谐波电流补偿环嵌入到从逆变器控制算法中，能有效抑制负载电压中的谐波分量。

6 结论

铁路牵引供电系统中存在的大量非线性负荷不仅会降低负载电压质量，也会影响到铁路牵引供电系统中对电能质量较为敏感的设备安全稳定运行。基于此，提出了一种充分利用PET 输出侧从逆变器剩余可用容量对电压谐波进行抑制的策略，所得出的结论如下：

1）将电能质量治理功能嵌入到PET 输出侧从逆变器中，避免了增加额外的电能质量治理装置，降低了系统成本。

2）主逆变器维持原有的控制策略不变，其中负载电流中的基波电流分量由PET 输出侧主、从逆变器共同承担，负载电流中的谐波电流分量则全部由PET 输出侧从逆变器承担，降低了主逆变器的备用容量。