复杂应力状态下金属材料屈服模型及有限元验证

刘彦杰，李明强，杨卫平

（航空工业第一飞机设计研究院强度设计研究所，西安710089）

0 引 言

金属延性断裂是飞行器金属实体类结构，例如接头、加强框等结构，最重要的破坏形式。复杂的结构细节特征及载荷作用形式对飞行器实体结构的精细化设计和验证提出了较高的要求。金属实体类结构的失效破坏属于金属材料在复杂应力状态下的失效破坏，试验研究表明，在不同应力状态下金属材料呈现出不同的屈服及破坏行为。利用精细有限元数值仿真预测金属结构延性断裂行为成为结构精细化设计的重要手段，其前提是建立合理的适用于复杂应力状态的金属屈服准则。只有在正确预测复杂应力状态下材料初始屈服以及后继屈服塑性硬化行为的基础上，才能进一步研究金属结构断裂行为。

经典von Mises理论（J2理论）认为，复杂应力状态下材料的弹塑性本构关系可以通过引入等效应力和等效应变的概念等价为一维问题，即单一曲线假设。然而，大量试验和理论研究表明，单一曲线假设并不能很好地描述材料在复杂应力状态下的弹塑性本构规律，金属屈服行为与应力状态有着密不可分的关系。目前国内外已有大量文献研究应力状态参数对金属材料屈服面的影响。最早受到关注的是静水应力（或应力三轴度）参数，并产生了多种基于静水应力（或应力三轴度）修正的von Mises模型：W.A.Spitzig等对铝合金和钢的研究表明静水应力显著影响金属材料的屈服应力，且认为两者线性相关；A.Needleman等基于细观孔洞损伤演化模型，提出了一种含损伤量的屈服模型，该模型认为静水应力对屈服面产生非线性影响，即屈服面随着静水应力的增加而收缩；K.Nahshon等进一步发展了Gurson理论。国内研究人员也对应力三轴度参数对金属屈服的影响进行了理论研究与试验研究。随着有关金属延性断裂研究的不断深入，Lode角参数对金属屈服和断裂的影响越来越受到人们的关注。最具代表性的研究工作有：Y.Bai等、L.Xue提出了一种包含应力三轴度和Lode角参数耦合的修正屈服模型；L.Xue还提出了一种与损伤变量耦合的弹塑性本构模型，间接体现了静水应力和Lode角参数对后继屈服切线模量的影响。但上述研究没有细致研究应力三轴度和Lode角参数影响金属屈服行为的差异性，而是直接将应力三轴度和Lode角参数耦合在一起共同影响金属初始屈服应力以及后继屈服演化，导致模型复杂、材料常数多且标定困难。

本文首先在文献［9］研究的基础上，结合铝合金AL 2024材料5种典型构形试验件进行拉伸破坏试验，研究应力三轴度和Lode角参数对金属材料屈服行为的作用方式；然后根据试验分析提出一种分别虑及应力三轴度对初始屈服应力和Lode角参数对塑性切线模量修正的屈服模型，并进行有限元与试验对比验证；最后对耳片结构拉伸试验进行有限元与试验对比分析，以验证本文提出的修正屈服模型的精度。

1 三维应力状态的表征参数

首先对三维应力状态在主应力空间的表征参数进行概要介绍。任意应力张量

σ

都可用三维主应力空¯ ¯¯间→ 中的向量表示其应力状态，如图1所示，向量

OA

表示应力状态(

σ

，

σ

，

σ

)，其中

σ

，

σ

，

σ

为主应力分量。图1中的

z

轴为等倾线，垂直于等倾线的平面称为等倾面；

p

为静水应力（材料受压缩时为正）；

σ

为Mises等效应力。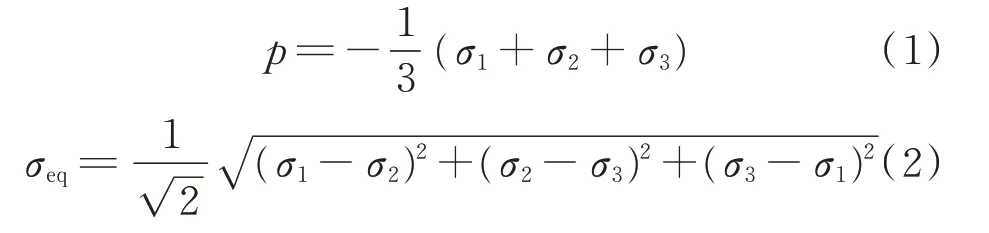

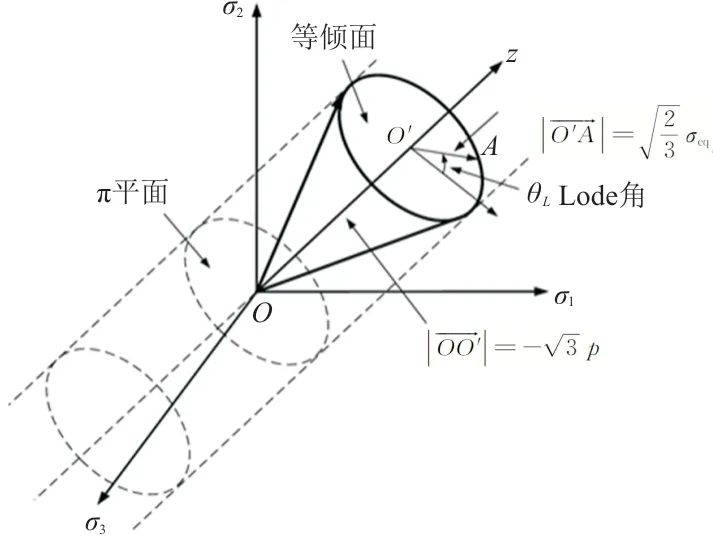
图1 应力状态在主应力空间中的表示Fig.1 Stress state in principal stress space

此外，在描述静水应力

p

时常用其无量纲形式，即应力三轴度

η

，定义如下：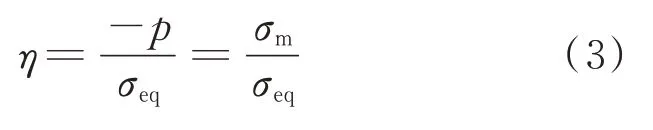

主应力状态(

σ

，

σ

，

σ

)在等倾面上的投影为主应力偏量(

s

，

s

，

s

)，如图2所示。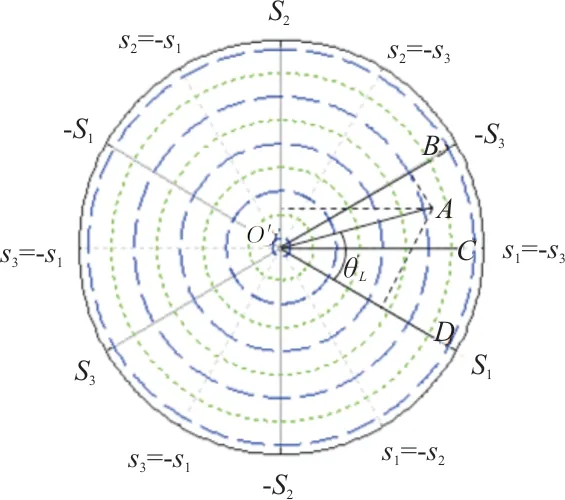

图2 主应力在等倾面内的投影以及Lode角Fig.2 Demonstration of Lode angle

在等倾面内，主应力偏量的分布情况可用Lode角

θ

表示，定义为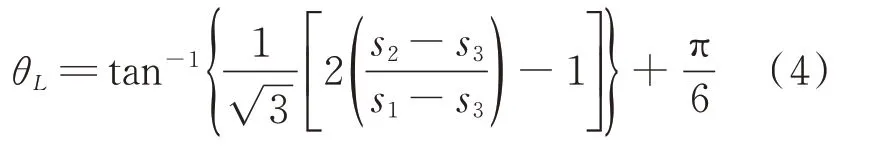

2 基于应力状态修正的金属屈服准则

试验和理论研究结果表明，应力三轴度（或静水应力）和Lode角参数会对材料的初始屈服和后继屈服产生不可忽略的影响。W.A.Spitzig等认为初始屈服应力随材料静水应力的变化而线性改变；Y.Bai等则认为应力三轴度和Lode角均会影响材料初始屈服和后继屈服行为，并给出了虑及应力三轴度和Lode角参数的修正屈服准则。本文结合试验和数值仿真研究发现，应力三轴度主要影响材料初始屈服应力值，而Lode角参数主要对后继屈服的塑性切线模量产生影响。

本文提出一种分别虑及应力三轴度对初始屈服应力以及Lode角参数对塑性切线模量影响的修正屈服理论。其中，初始屈服应力修正表达式为

由式（6）可得，当应力三轴度

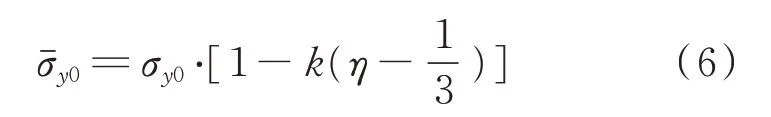
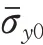
η

为1/3时（光滑圆棒拉伸应力状态），该修正初始屈服应力与材料标准试件初始屈服应力相同。试验结果表明，

k

通常是一个正数，当应力三轴度增加时，材料实际的初始屈服应力降低。

后继屈服的塑性切线模量修正表达式为

式中：

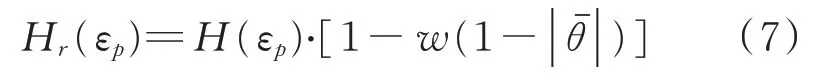
H

为由光滑圆棒拉伸试验获得的材料塑性切线模量；

H

为虑及Lode角影响的修正塑性切线模量；修正系数

w

为材料常数。

式中：

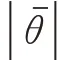
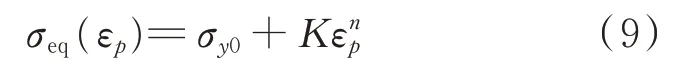
σ

、

K

和

n

为材料常数。

综上所述，结合初始屈服应力与塑性切线模量修正，本文提出的修正屈服应力表达式为

式中：

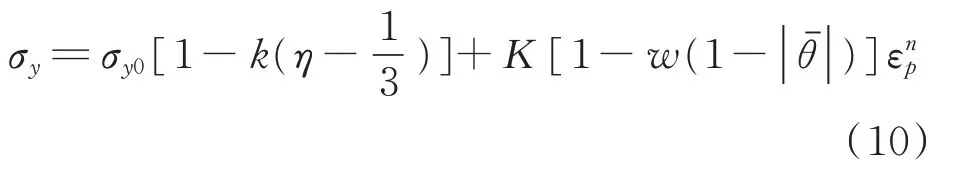
σ

、

K

、

n

、

k

和

w

为屈服准则常数，其中前三个常数为经典Mises屈服准则常数，后两个常数为修正常数。

由式（10）可知，修正的屈服面可写为

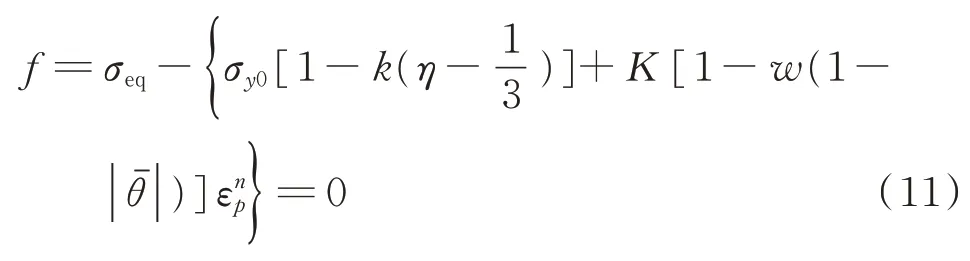
根据相关联的Prandtl-Reuss塑性流动增量理论，塑性应变增量可写为

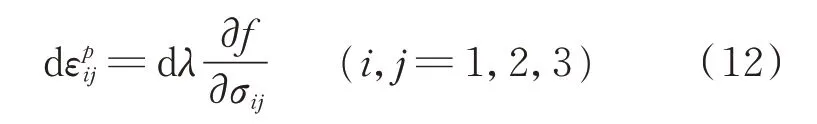
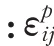
通过张量求导计算，可得

该屈服准则中将应力三轴度与Lode角参数的影响解耦，不仅减少了模型的材料常数，还有利于简化材料标定试验及数据处理过程。

3 复杂应力状态金属拉伸试验

以航空航天领域常用的AL2024-T 4铝合金材料为例，对包含光滑圆棒、带缺口圆棒、带缺口槽平板等五种不同构形的元件级试验件进行拉伸试验，研究不同应力状态下金属构件的屈服行为。详细的试验件构型、试验内容和结果参见文献［13］。

4 元件试验与分析结果对比

以ABAQUS/Explicit求解器为平台，采用VUMAT用户材料子程序开发修正屈服准则算法，对第3节所述5种典型构形元件级试件拉伸试验进行数值模拟，检验第2节提出的修正屈服准则对复杂应力状态下材料屈服行为的预测精度。

由于试验件构型和受载的对称性，本文采用4结点轴对称单元建立圆棒模型，采用8结点实体单元建立平板模型，所有模型在缺口区域内进行网格细化。有限元模型在一侧固支，另一侧加载，并施加对称约束。

结合试验结果与有限元数值分析，可获取修正屈服准则常数。以铝合金AL 2024材料为例，修正屈服准则的材料常数为：

σ

＝380 MPa，

K

＝328 MPa，

n

＝0.22，

k

＝0.5，

w

＝0.2。分别采用传统von Mises屈服准则、只对初始屈服应力修正的屈服准则（式（6））、以及初始屈服应力和塑性切线模量同时修正的屈服准则（式（6）和式（7））进行对比分析，数值仿真结果如图3~图7所示，图中横轴表示引伸计位移；图例“

η

修正”表示只修正初始屈服应力，“

η

和

θ

修正”表示同时修正初始屈服应力和塑性切线模量。各类型构件真实试验与模拟计算误差详见文献［13］。

图3 光滑圆棒试验与数值模拟的载荷—位移曲线对比Fig.3 Comparison of test and simulation of smooth bar in force-displacement curves

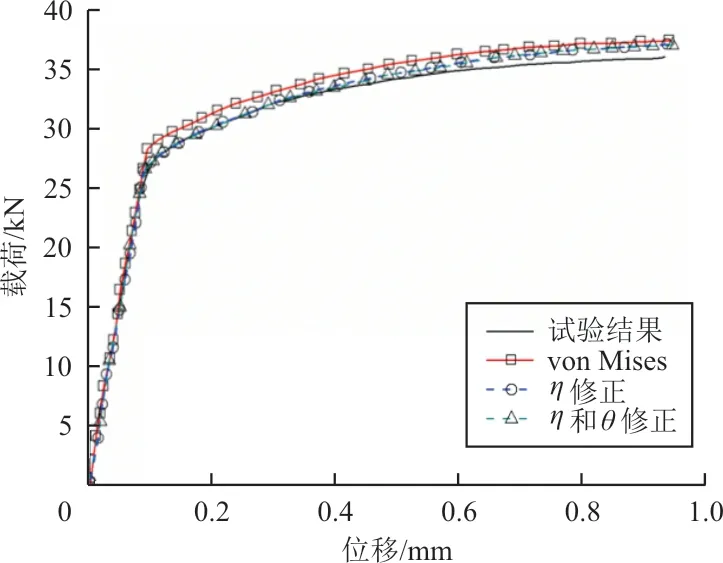
图5 大缺口圆棒试验与数值模拟的载荷—位移曲线对比Fig.5 Comparison of test and simulation of large notched bar in force-displacement curves

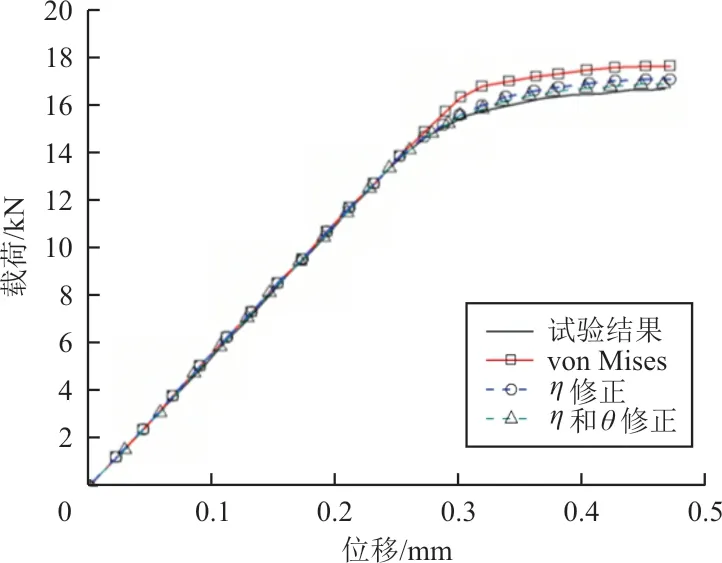
图7 大缺口槽平板试验与数值模拟的载荷—位移曲线对比Fig.7 Comparison of test and simulation of large grooved plate in force-displacement curves

图6 小缺口槽平板试验与数值模拟的载荷—位移曲线对比Fig.6 Comparison of test and simulation of small grooved plate in force-displacement curves

数值计算与试验结果的误差如表1~表2所示，可以看出：对于初始屈服应力，最高误差出现在应力三轴度最高的小缺口圆棒和小缺口槽平板试件上，误差分别为8.21%和13.56%；但对于光滑圆棒试件，由图3及表1的数据可得，数值模拟与真实试验误差极小。据此可得出基于单一曲线假设的von Mises屈服理论在材料处于一维应力状态下能与真实试验精确符合，然而却不足以适应更常见的复杂应力状态。

表1 试验与模拟结果的初始屈服载荷误差Table 1 Error of test and simulation in yield strength

表2 试验与模拟结果的破坏载荷误差Table 2 Error of test and simulation in failure strength

从数值预测与试验结果的对比中可以看出，不同准则的精度差异主要体现在对带缺口圆棒和带缺口槽平板试验件的预测上。对于初始屈服而言，经典von Mises准则在预测缺口半径小、应力三轴度大的试验时存在较大误差，带小缺口的圆棒和平板试验的误差均超过了8%。通过引入应力三轴度参数对von Mises初始应力进行修正后，明显提高了带缺口试验件初始屈服载荷的预测精度。

对比缺口圆棒试验和缺口槽平板试验发现，初始屈服修正准则对缺口圆棒试验的预测精度要高于对缺口平板试验的预测精度。这说明虽然应力三轴度和Lode角对材料初始屈服均产生影响，但应力三轴度对初始屈服应力的影响起主导作用。Lode角更重要的作用体现在对塑性流动（即塑性切线模量）的影响上，这也是本文修正屈服准则的试验基础。

对于试验件后继屈服塑性流变行为，从图4~图7以及表2可以看出：只修正初始屈服应力的准则已经能很好地符合缺口圆棒试验件后继屈服阶段的塑性硬化曲线，在此基础上引入Lode角对切线模量的修正，基本没有改善缺口圆棒试验的预测精度；但切线模量修正明显提高了带缺口槽平板试验塑性硬化阶段的预测精度。从表2可看出：切线模量修正使带缺口槽平板试件断裂载荷的数值预测误差降低至2%左右。

图4 小缺口圆棒试验与数值模拟的载荷—位移曲线对比Fig.4 Comparison of test and simulation of small notched bar in force-displacement curves

上述研究表明，塑性切线模量修正对提高材料复杂应力状态下塑性流动行为的预测精度具有重要意义。

5 耳片结构试验与分析验证

选取典型金属耳片拉伸试验，应用本文提出的修正屈服准则对耳片结构屈服过程进行研究，并与试验结果、经典von Mises屈服准则以及Bai-Wierzbicki屈服准则的分析结果进行对比。

耳片结构平面尺寸及加载方式如图8所示，耳片厚度为10 mm；结构左端固支，右端通过接触将销钉的位移加载传递到耳片结构上，加载方向与耳片轴线呈5°夹角。耳片材料为铝合金AL2024，其具体的材料属性见第4节所述。销钉材料为合金钢，其弹性模量为210 GPa，泊松比为0.3。

图8 耳片结构平面尺寸及加载方式示意Fig.8 Sketch of the size and loading of lug structure

应用本文提出的修正屈服准则的分析结果与试验结果对比如图9所示，图中同时给出了经典Mises屈服准则、Bai-Wierzbicki屈服准则的分析结果。

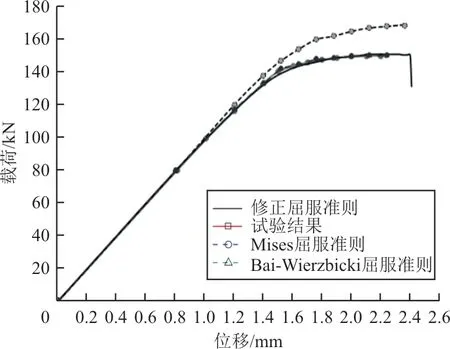
图9 耳片结构拉伸试验与数值分析结果对比Fig.9 Comparison of experiment and simulation of lug structure

从图9可以看出：经典Mises屈服准则预测的载荷—位移曲线与试验结果在弹塑性阶段存在明显偏差，而本文提出的修正屈服准则与Bai-Wierz‐bicki屈服准则分析结果基本一致，且和试验结果吻合较好，表明基于应力状态修正的屈服准则能够显著提高复杂应力状态金属结构弹塑性行为。对比本文提出的修正屈服准则与Bai-Wierzbicki屈服准则，结果表明本文提出的应力三轴度和Lode角参数分别对初始屈服应力与后继屈服斜率的解耦准则的合理性。本文的解耦修正准则不仅形式变得更加简洁，同时也简化了准则标定的元件试验规模，更有利于工程应用。

6 结 论

（1）对于三维复杂应力状态下的拉伸试验，使用经典von Mises屈服准则时，有限元模拟计算的初始屈服应力以及后继屈服应力结果与试验结果存在较大差异，揭示了应力状态是影响材料屈服及塑性流动的一个重要因素。

（2）本文结合试验研究，发现应力三轴度主要影响材料初始屈服应力，Lode角参数主要影响切线模量，并提出了一个虑及两者的修正von Mises屈服准则，给出了修正准则的塑性流动方程。

（3）试验与有限元对比分析表明该准则能够很好地预测复杂应力状态下金属结构的初始屈服及后继屈服塑性硬化行为，对工程应用有较高参考价值。