引入旅游偏好的城际客运出行分布预测模型
陶思然,叶霞飞
(同济大学,道路与交通工程教育部重点实验室,上海201804)
0 引言
随着社会经济的快速发展,城市群正在成为快速带动经济发展的增长极。在我国,以城市群为主体构建大中小城市和小城镇协调发展的城镇格局将逐步形成,此过程将通过城市间的频繁交流而实现,大量的城际客运交通需求应运而生。然而,作为城际客运出行需求预测的重要环节,城际客运出行分布预测研究目前还不完善,一个较为突出的问题是,对可以将出发城市与到达城市关联起来的因素考虑不足。可以借助城际客运出行分布预测中较为常用的模型之一重力模型[1]对该问题进行说明。自1946年Zipf[2]发现,城际客运量与两个城市人口的乘积成正比,与两个城市间的距离成反比后,这种规律随着后续研究的开展,同时参考物理学重力模型,慢慢演变为今日的重力模型,即两个城市之间的客流交换量与起点城市的出发量、终点城市的到达量成正比,与两个城市间的出行阻抗成反比。出行阻抗一般由两个城市间出行所花费的时间、金钱、所使用交通方式的舒适度等因素决定。可以看出,此时仅有城际广义出行阻抗由出行的两个端点共同决定,可以解释为何一个城市能更多地与特定城市发生关联。
但事实上,在四阶段模型体系中,质量项的研究在出行生成阶段已完成,故可知在出行分布预测模型中,仅考虑出行阻抗这一个关联性因素是不足的[3]。针对这种不足,陶思然等[4]从城际客运出行主要的出行目的出发,抽象出一些主要的关联性影响因素,例如政治关联因素、母子公司关联因素、产业关联因素、生存关联因素、旅游关联因素等。
本文主要针对旅游关联因素进行研究。假日旅游出行已有大量文献进行研究,但随着社会生产力的发展,自由职业者增多,年休假制度普及,交通设施日臻完善,平常的工作日及周末也会有数量可观的旅游出行。例如,日本第5 次(2010年)全国干线旅游纯流动调查将出行目的分为公务、旅游、私人、其他与不明这5 类。调查数据显示,平常工作日有约2/5的OD对间城际旅游目的出行量占城际全目的总出行量的比例超过20%,平常周末城际旅游出行量占比更高。对于国内而言,仅考虑长三角26市范围内,南京市一个平常工作日城际到达量约43万人次,而南京市5A和4A级景点同一日接待同范围内城际游客约13万人次。尽管这13万人次不一定都是当天出行,但由于长三角地区交通设施较为完善,彼此联系也较为紧密,故当日出行者应该占有一定的比重。由于这部分出行拥有独特的关联机制,在模型中体现两个城市间因旅游而产生的关联性就显得非常重要,这种重要性可以通过下例进行说明:假设有A、B、C、D这4座城市,其中,A和B拥有旅游资源,C和D完全没有旅游资源,则C城市与D 城市之间应该不存在旅游客流交换量。然而,由于C、D 两座城市与A、B 两座城市之间将存在旅游客流交换量,即在C、D 两座城市的出发、到达总量中,将包含一定量的旅游客流。因此若采用基本重力模型,将使C城市与D城市之间的预测客流交换量中包含旅游客流交换量,从而导致其客流预测结果偏大。
目前,已有部分学者重点关注了出发地与到达地之间的旅游关联性,并得到一定的研究成果。有部分学者将网络搜索指数作为变量加入模型,例如,单德朋等[5]认为,谷歌搜索指数可以作为旅游地宣传促销努力程度的度量。但网络搜索指数的关键词收集和选取方案还未形成成熟的体系[6]。文化距离也是建立出行两端关联关系常用的影响因素,例如,毕娟[7]认为两地间文化维度的差异可以解释中国入境游客的客源地分布,且文化距离和目的地选择行为呈倒“U”型关系。但文化距离的计算依赖于主观的文化差异测量指标,需要通过调查问卷获取数据,目前为止更适用于入境旅游研究。资源异质性则一直被旅游学科研究者认为可以解释特定城市对间的旅游关联。例如,陈洁[8]利用余弦相似度将旅游资源异质性化为因子加入重力模型,对每个城市的吸引力进行修正。但资源异质性的评判标准缺乏合理度量,其仅将景点分为自然景观类景点、人文景观类景点与休闲活动类景点,每个类别内部仍然可能存在异质性。
综上所述,既有研究提出的关联项存在不成熟、适用范围受限和度量标准不合理等问题,故本文试图提出一个新的关联项,以表达各个城市对其他城市的旅游偏好,并将其加入城际客运出行分布预测模型中,以体现客源地与旅游地之间的关联性对城际客运出行分布的影响。
1 基础数据来源
本文借助长三角26 个城市的数据开展研究,即:上海、南京、无锡、常州、苏州、南通、盐城、扬州、镇江、泰州、杭州、宁波、嘉兴、湖州、绍兴、金华、舟山、台州、合肥、芜湖、马鞍山、滁州、安庆、铜陵、池州、宣城。考虑到秋日环境较为适宜旅游,夏日学校放暑假,同时避开下雨日,最终将数据获取时间确定为2019年7月24日(周三)、7月28日(周日)、10月24日(周四)和10月26日(周六)。如无特殊说明,后文所述“其他城市”“城际游客”等概念时,皆指研究范围和研究日期内的其他城市和城际游客。
1.1 城际客运出行OD数据
本文所利用的OD 出行数据为手机信令数据,由联通公司旗下智慧足迹科技有限公司依托联通手机用户的移动轨迹,确定当日跨行政边界的出行量,再根据起点城市和终点城市的联通用户市场占有率进行扩样而得。
1.2 景点游客数据
本文对各城市旅游偏好的研究,需要借助各个城市的景点从其他城市吸引到的游客数据来进行。根据国家标准《旅游区(点)质量等级的划分与评定(GB/T 17775-2003)》,我国旅游景区质量等级划分为5 个等级,由高到低依次为AAAAA(5A)、AAAA(4A)、AAA(3A)、AA(2A)、A 级旅游区(点)。该标准规定,5A与4A级景点的年游客量分别需达到60 万人次与50 万人次,远超过3A(30 万人次)、2A(10万人次)与A(3万人次)级景点,且知名度总体上更高,吸引城际游客的能力更强,故本文选取研究范围内所有的5A 和4A 级景点进行研究。后文所述“全市景点总个数”“全部景点城际总旅游客流量”等概念时,皆指该城市内所有5A 和4A 级景点数以及该城市内所有5A 和4A 级景点的城际总体旅游客流量。
景点游客数据是指,目标日出现在景区的各城市游客数量。其中,游客来源地判断标准为其常住地,即游客1年内居住时长大于6 个月的城市。判断其为游客的标准为,在目标日进入景区范围并停留超过1 h。舍弃部分用地性质复杂以致无法判断进入者是否为游客的景点,例如无法仅统计进入上海金茂大厦88 层观光厅的联通用户,故该景点舍去。最终得到共计513 个景点的当日游客的常住地数据。
1.3 出行阻抗数据
本文中广义出行阻抗由两个城市间各交通方式的出行时间和费用构成。考虑的交通方式包括:铁路列车、私家车、长途巴士。其中,铁路列车数据来自铁路12306网站;私家车出行时间数据自百度地图爬取,出行费用数据依赖百度地图爬取路线计算高速通行费及油耗费用;长途大巴数据参考巴士管家网、114 票务网、客运站网、快票出行APP 等多个网络平台的数据。每种交通方式的广义出行费用计算方法为:出行费用+出行时间×时间价值。其中,时间价值为出发城市与到达城市2019年人均可支配收入的均值。收入数据来源于各个城市的统计年鉴。最终,每个OD对间广义出行费用为各交通方式广义出行费用的均值。
2 旅游景点城际游客客源地分布特征分析
从文献综述不难看出,目前仍然很难提取出一个能够有效表达两地之间旅游关联的变量,此问题在集计模型中更为凸显,因为旅游是人们出于主观意愿所进行的活动,客观上并不存在一个因素使得某个地区的人“必须”去另一个地区旅游。但通过对各景点城际游客客源地分布数据进行分析后发现,尽管旅游行为受旅游者的主观意愿支配,但城际游客客源地分布在集计层面上仍然呈现出较强的规律性。以南京市为例说明,图1为2019年7月24日、7月28日、10月24日和10月26日这4个分析日内,南京市5A和4A级景点的城际游客客源地分布数据。
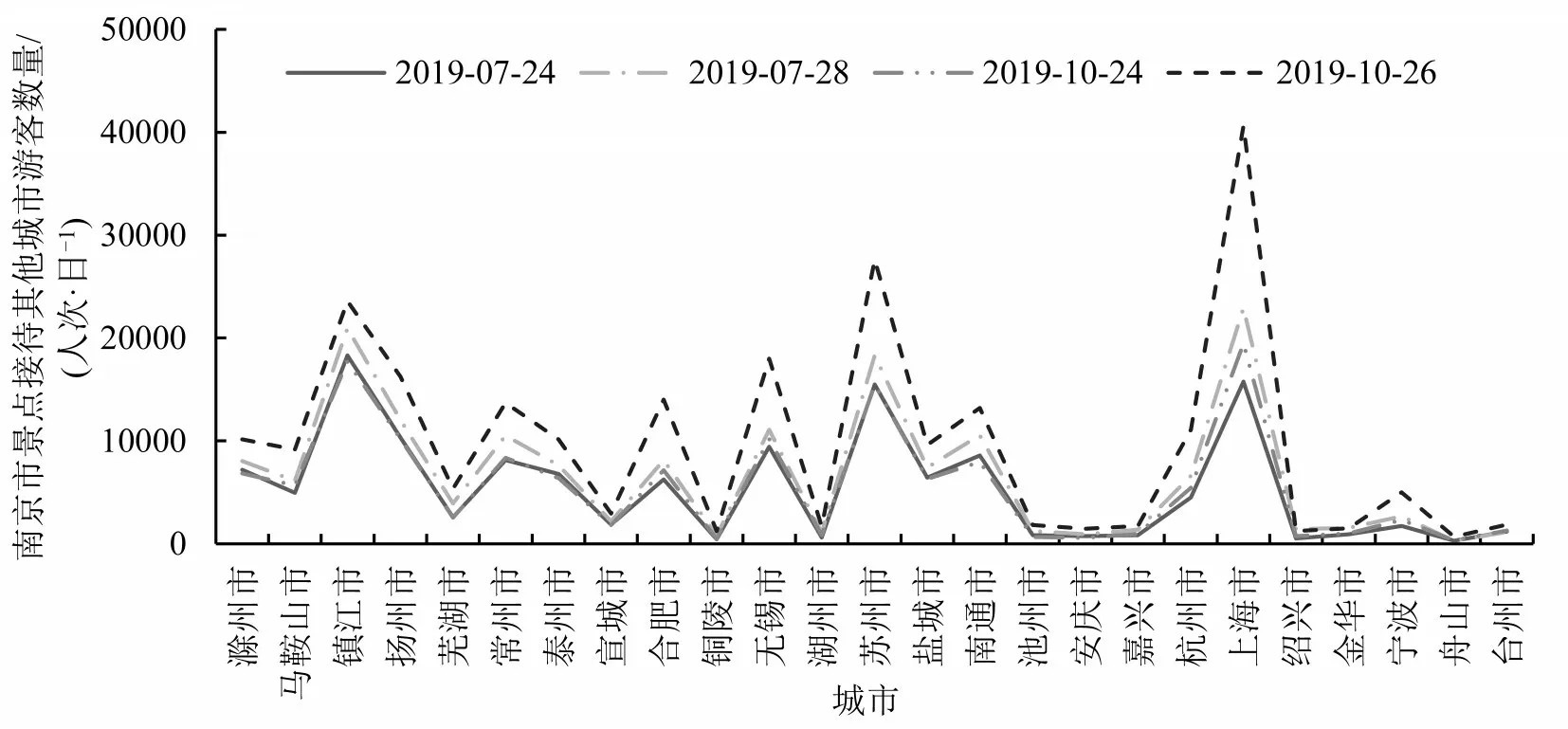
图1 南京市5A和4A级景点客源地分布Fig.1 Spatial patterns at 5A and 4A tourist attractions in Nanjing
如图1所示,在4个研究日期内,南京市城际游客客源地分布大致相同,仅仅在数量上有所差异。本文采用相关系数ρ和差异系数λ描述客源地分布数列之间的差距。假设为某日某城市的城际游客客源地分布向量,为同一城市不同日期的城际游客客源地分布向量,其中,xi和yi皆按照与目标城市距离由近及远顺序进行排列。相关系数ρ和差异系数λ的计算公式为
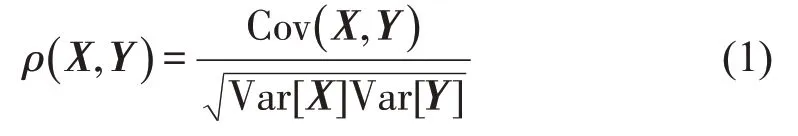
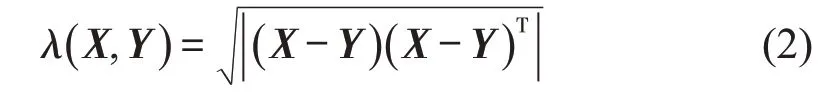
相关系数ρ用来衡量X与Y变化趋势的接近程度,差异系数λ用来衡量每个组成元素的差异。综合ρ和λ可以表示两个序列的相似程度。图1中南京市4 d数据之间的关系如表1所示。

表1 南京市不同日期城际游客客源地分布之间的ρ 与λTable 1 ρ and λ between spatial patterns of intercity tourists on different dates in Nanjing
从表1可以看出,虽然数据的日期分别属于暑期工作日、暑期周末、金秋工作日、金秋周末,但南京市城际游客客源地分布情况相差不大。
为分析城市单个景点与城市所有景点的城际游客客源地分布情况,表2给出南京市各景点与南京市整体城际游客客源地分布间的ρ与λ。从表中可以看出,南京市城际旅游客流量较大的景点,不同日期的客流规律性都比较强,各个客源地分布占比相差也较小;而城际旅游客流量较小的景点,则没有明显倾向,可能具有规律性,也可能不具有规律性。如果一个景点的ρ与λ可以满足ρ≥0.8,λ≤0.2,且该景点同时满足城际旅游客流量大于等于该市所有景点城际旅游客流量的均值,即将其定义为头部景点,则南京市头部景点共11个,占全市景点总个数的44%,其城际旅游客流量却占全部景点城际总旅游客流量的89%。说明南京市不同日期城际游客客源地分布规律是由头部景点决定的。

表2 南京市各景点与南京市整体城际游客客源地分布间的ρ 与λTable 2 ρ and λ between spatial patterns of intercity tourists of each attraction and Nanjing
其他城市也存在类似规律。如果考虑研究范围内全部513 个景点,共163 个景点符合头部景点标准,占全部景点的32%,其城际旅游客流量却占全部景点城际总旅游客流量的82%。
综上所述得到以下基本结论:
(1)一个城市的城际游客客源地分布规律虽然受到旅游者个人主观因素的影响,但从整体上来看仍会呈现出较强的规律性。
(2)一个城市的城际游客客源地分布规律主要由头部景点决定,而这些头部景点的城际游客客源地分布往往较为接近,这可能是由于这些景点名气更高,交通可达性更好,故从统计学角度来看,非过夜旅游者在游览时去往这些景点的概率是相等的,过夜游客可能在一次旅行中将这些景点都游览一遍。
由此可见,在中国目前环境下,一个城市的城际游客客源地分布主要由头部景点决定,而大部分头部景点已经存在相当长的一段时间,城际游客的客源地分布较为稳定。基于上述特征,可以借助一个城市旅游景点的城际游客客源地分布构建其他城市居民对该城市的旅游偏好,为城际客运出行分布预测模型更好地描述旅游关联的影响奠定基础。
3 引入旅游偏好的城际客运出行分布预测模型构建与分析
3.1 亲景度概念
亲景度是马耀峰等[9]在研究入境旅游时提出的概念,该指标利用客源国在某国的某个目标城市的外国游客占比与客源国在该国的外国游客占比,反映客源国游客对目标国不同城市的旅游偏好程度。假设到某地的某旅游客源国人数为Mi,到某地的外国游客人数为M1,到该地所在国旅游的某客源国人数为Gi,到该地所在国旅游的外国人数为G1,则亲景度L的计算公式为

本文研究范围内各城市之间交流紧密,对彼此景点信息获取渠道较多,获取速度较快,按照常理,人们出游应当更加随心所欲,使景点客流失去规律性。但是由第2节研究结果可知,从整个城市角度来看,城际游客客源地分布是较为稳定的。这反而说明,这种稳定的规律性体现了一个地区居民的旅游偏好,因此,可以引入亲景度的概念,基于城际游客客源地分布特征,在集计层面上构建一个变量,用以表达一个城市的居民出于文化、历史等原因,对其他城市的旅游偏好。
3.2 模型构建
假设城市i对城市j的亲景度为Li→j,表达式为

式中:xi→j为i城市居民在j城市旅游景点出现的数量(人次·d-1)。
根据亲景度构建两个城市之间的旅游偏好为
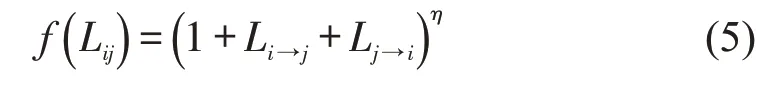
式中:Lij为城市i与城市j之间基于亲景度的旅游偏好变量;Li→j为城市i对城市j的亲景度;Lj→i为城市j对城市i的亲景度;η为待标定系数。
因此,构建引入旅游偏好变量的城际客运出行分布预测模型。
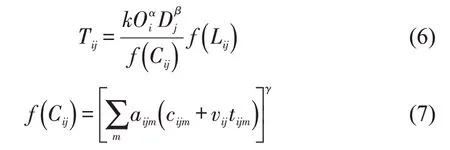
式中:Tij为城市i到城市j单日出行交换量(人次·d-1);Oi为城市i单日出行出发量(人次·d-1);Dj为城市j单日出行到达量(人次·d-1);f()Cij为城市i与城市j之间的广义出行阻抗;f()Lij为两个城市之间的旅游偏好;aijm为交通方式m的权重,本文按均值进行计算;cijm为交通方式m在两地间的出行费用(元);vij为城市i与城市j的时间价值均值(元·h-1);tijm为交通方式m在两地间的出行时间(h);k,α,β,γ,η为待标定系数。
首先利用长三角26 城市全目的出行OD 数据以及5A 和4A 级景点的城际游客客源地分布数据进行模型系数标定,再利用标定完成的模型计算城际客运出行分布预测值。考虑到矩阵的行约束和列约束,利用Fratar 迭代得出最终的城际客运出行分布预测值。评判模型预测能力的标准可采用R2以及预测前后城际客运出行分布量的标准误差σ,σ的表达式为
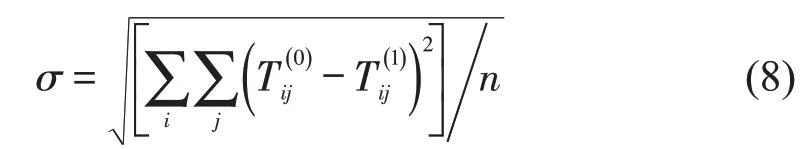
3.3 模型预测结果及分析
采用最小二乘法对模型进行标定,即利用取对数方法将式(6)演变为

第2节已经说明,不同日期的城际游客客源地分布基本没有差别,故此处仅使用2019年7月24日的数据对模型进行标定。
首先对各变量进行相关性检验和多重共线性检验,检验结果如表3所示。
从表3 可以看出,各变量的方差膨胀因子(Variance Inflation Factor,VIF)都小于10,说明多重共线性并不严重,可以进行回归。对基本重力模型和加入旅游偏好变量的重力模型分别进行标定,得到结果如表4所示。

表3 各变量相关性检验和多重共线性检验Table 3 Bivariate correlation between variables and multicollinearity of variables
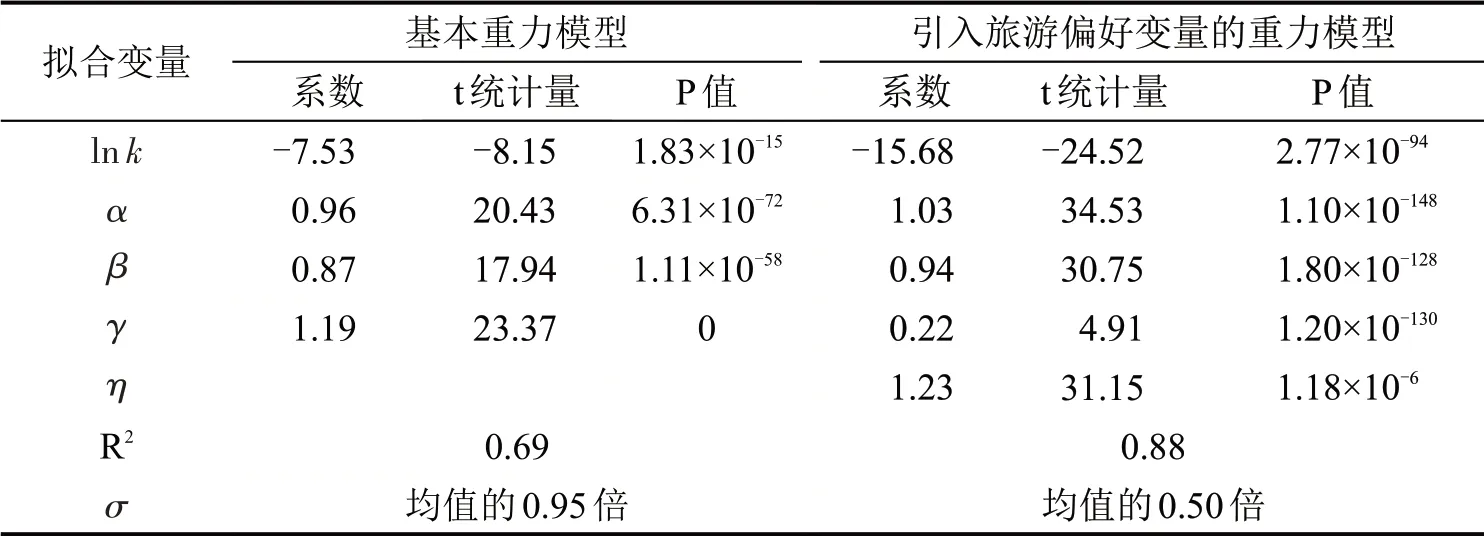
表4 加入旅游偏好变量前后模型标定结果对比Table 4 Calibration of gravity model with and without tourism preference
从表3 和表4 可以明显看出,加入亲景度相关的旅游偏好变量后,与基本重力模型相比,模型R2从0.69上升至0.88,标准误差从现状交换量均值的0.95倍下降至0.50倍,证明该变量对提升城际客运出行分布预测模型精度十分有效。
参与标定的OD 对共649 个,在引入旅游偏好变量后,误差减小的OD 对为486 个,占所有OD 对的75%;误差增大的OD 对为163 个,占所有OD 对的25%。分别计算绝对误差与相对误差。绝对误差为每个OD 对间的预测出行量与实际出行量之间差值的绝对值,相对误差为每个OD对间的绝对误差除以其实际出行量,则不同OD对间的绝对误差与相对误差均值如表5所示。

表5 不同OD对的绝对误差与相对误差Table 5 Absolute error and relative error of different OD pairs
从表5可以看出:对于引入旅游偏好变量后误差减小的OD 对而言,其误差降低幅度较大;对于误差增大的OD对而言,虽然误差增大的幅度也较大,但由于其绝对值较小,故研究范围内OD 对间误差整体呈较为显著的下降趋势,证明该变量对改善城际客运出行分布预测模型的预测能力具有较为显著的效果。
需要注意的是,虽然城市的城际游客客源地分布较为稳定,但是由不同季节或工作日、双休日导致的城际出行者数量差距还是较大的,在使用绝对数据建模时应当针对不同日期分别标定。
4 结论
本文针对目前城际客运出行分布预测过程中对城际旅游关联性考虑不足的问题,提出一个可以表征两个城市间旅游关联性的旅游偏好变量,并以此为基础构建了城际客运出行分布预测改进模型。
(1)借助手机信令数据,通过对长三角26 个城市范围内的5A 和4A 级景点城际游客客源地分布进行分析后发现,虽然旅游是一项主观的活动,但在集计层面上,同一个城市中的头部景点均呈现出相近且稳定的客源地分布规律;长三角26 个城市范围内头部景点城际旅游客流量占全部5A 和4A级景点城际总旅游客流量的比例达到82%,其中南京市的这一比例达到了89%。由此可见,一个城市的城际游客客源地分布主要是由头部景点决定,其城际总体游客客源地分布也呈现出与头部景点相似的规律。另外,从暑期工作日、暑期周末、金秋工作日、金秋周末4 d 的数据来看,在非节日情况下,上述规律也非常稳定。
(2)基于长三角26个城市范围内5A和4A级景点城际游客客源地分布规律,借助亲景度指标,提出可以表征城际旅游关联性的旅游偏好变量,构建了在基本重力模型中引入旅游偏好变量后的城际客运出行分布预测模型。利用长三角26个城市的出行分布现状数据对模型进行标定后发现,与基本重力模型相比较,模型R2从0.69 上升至0.88,标准误差从现状交换量均值的0.95倍下降至0.50倍;误差减小的OD对占全部OD对数量的75%。由此可见,旅游偏好变量的引入对提高城际客运出行分布预测模型的精度是有效的。
然而,对于城际客运出行分布预测而言,城市间的旅游关联性因素仅仅是出行分布众多影响因素中的一个,本文建立的模型也仅仅说明了引入旅游关联性因素的重要性,所以今后还应继续对影响城际客运出行分布的城市间其他主要关联性因素逐一加以研究,并对研究成果进行融合,从而构建更加完善的城际客运出行分布预测模型。
——以山东省长岛县为例

