多信号交叉口干线行程时间特性分析

王福建，卢一笑，金盛

(浙江大学，建筑工程学院，杭州310058)

0 引言

行程时间及其可靠性是交通运行状态评价、交通系统性能评估的重要指标之一。从管理者角度来说，通过对行程时间的分析是支撑交通规划、设计与管理政策制定的重要基础；从出行者角度来说，行程时间的信息获取是制定出行计划、选择出发时刻、规划出行路径的重要依据。

关于行程时间分布的研究，最初的观点认为正态分布是合适的。之后，许多研究观察到行程时间存在偏态分布现象，因此对数正态分布、Weibull分布、Gamma 分布等被应用到拟合行程时间数据中。Taylor等[1]对阿德莱德两条主干道的GPS数据进行分析得到，双参数Burr分布较对数正态分布可以更好地表示行程时间右偏的特点，且这种分布还为使用基于百分位值的可靠性评价指标提供了计算优势。Susilawati[2]随后表明，Burr 分布可以拟合大部分观测到的行程时间变异性。向文凯[3]对比了伽马、正态、对数正态、Weibull 分布后得到Burr 分布是最为理想的城市行程时间分布拟合模型。Zhen[4]分析了不同时段、不同星期、不同位置及不同天气条件下的行程时间分布，结果表明，Burr 分布的拟合效果最佳。城市道路的交通流更为复杂，由于受到信号交叉口、出入口及行人过街等因素影响，呈现出多峰特性，混合分布模型[5-6]被认为可以更好地反映城市间断流行程时间特征，Peng[7]表明混合概率模型不仅具有较好的统计拟合效果，且能反应交叉口信号控制的影响。综合以上研究，Burr分布相较于其他单峰分布模型的拟合效果更好，在复杂道路条件下，混合分布模型可以更好地描述行程时间分布特征。

进一步，有研究发现行程时间特性与交叉口数量或者路段长度之间存在一定的关系。Taylor等[8]验证了城市主干道上的车辆行程时间服从双峰分布，但其进一步研究发现，将处于同一信号控制系统下的路段连接起来，其行程时间分布的双峰性概率降低，在部分长路段上，双峰性现象被打破。同样，刘迎[9]通过GPS数据拟合发现，随着距离增大，交叉口数量增多，行程时间双峰分布特征减弱，红灯延误对行程时间的影响减小。陈明明[10]分析发现，缓冲时间指标与路段长度呈负相关关系，即路段越长，可靠性越高。由于数据质量有限，已有研究大多是研究单个路段或整条路径的行程时间特性，缺少对行程时间特性与其影响因素之间的定量分析。

本文基于杭州市萧山区的车牌识别数据获得不同交叉口数量、不同路段长度的行程时间数据，利用Burr 分布和高斯混合分布分别对路段和干线的行程时间分布进行拟合和特性分析。进一步利用灰色关联方法挖掘交叉口数量、干线长度和干线流量与行程时间分布特性及可靠性之间的关系。

1 车牌识别数据及处理

1.1 行程时间描述

杭州市萧山区各交叉口布设了电子警察摄像机，一般布设在信号交叉口进口道停止线上游约20 m的位置，其抓拍系统可以拍摄车辆通过停车线时的视频信息，自动识别得到车牌数据，因此可以收集车辆牌照、过车时刻、交叉口点位、进口道方向等信息。通过车牌匹配计算得到车辆通过两个连续交叉口的时间，从而获得车辆在目标路段上的行程时间。

本文路段行程时间是指车辆从上游交叉口停止线到下游交叉口停止线的运行时间，多信号交叉口干线行程时间是指车辆通过多个连续信号交叉口的运行时间。

1.2 数据预处理

通过上、下游交叉口识别数据进行车牌匹配，计算得到路段行程时间数据。由于红灯时间停车影响，车牌识别数据存在重复冗余数据，故需对车牌、卡口名称等信息一致且相邻检测时间差小于阈值的数据进行去重处理。同时需要去除行程时间异常的数据，剔除未准确沿路段行驶且发生停车的车辆数据，以避免产生偏差。行程时间异常值的处理过程分为以下几个步骤[11]。

Step 1 设定时间窗为10 min。

Step 2 粗过滤，剔除明显异常值。设置行程时间上限值，将车辆行车速度为5 km·h-1所产生的行程时间值记为上限值Tu，计算公式为

式中：Li为第i个路段的长度；Vl为该路段车辆行车速度下限值，即5 km·h-1。设置行程时间下限值，选取行程时间的第10%分位值作为下限值TL。通过设置行程时间上、下限值，剔除不在此区间的数据。

Step 3 利用莱茵达(即3σ)准则对数据进行过滤，选取第j个时间窗内的行程时间样本集TT, j，计算TT, j中数据的平均值Tmean和标准差判别依据为：若，则该数据的误差较大，属于异常数据，应剔除；若，则该数据在可接受范围内，应保留。通过莱茵达准则过滤掉距均值3 倍标准差以外的行程时间数据，重复多次，可以有效去除行程时间异常值。

根据以上步骤，设定时间窗为10 min，根据行程时间上、下限值剔除明显异常值后，重复4 次Step 3对行程时间数据异常值进行过滤使数据样本趋于稳定，即完成行程时间数据处理，效果如图1所示。

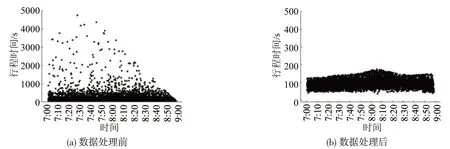
图1 数据处理效果Fig.1 Effect of data processing

1.3 数据描述

为减弱交叉口信号控制因素的影响，选取萧山区内3条信号协调控制的干线：市心路(山阴路-建设四路段)、市心路(振宁路-奔竞大道路段)、金鸡路(金惠路-恒枫路段)为研究对象。编号各交叉口表示研究路段，例如山阴路交叉口-金城路交叉口路段表示为A1-A2。各交叉口名称及编号如表1所示，位置如图2所示。

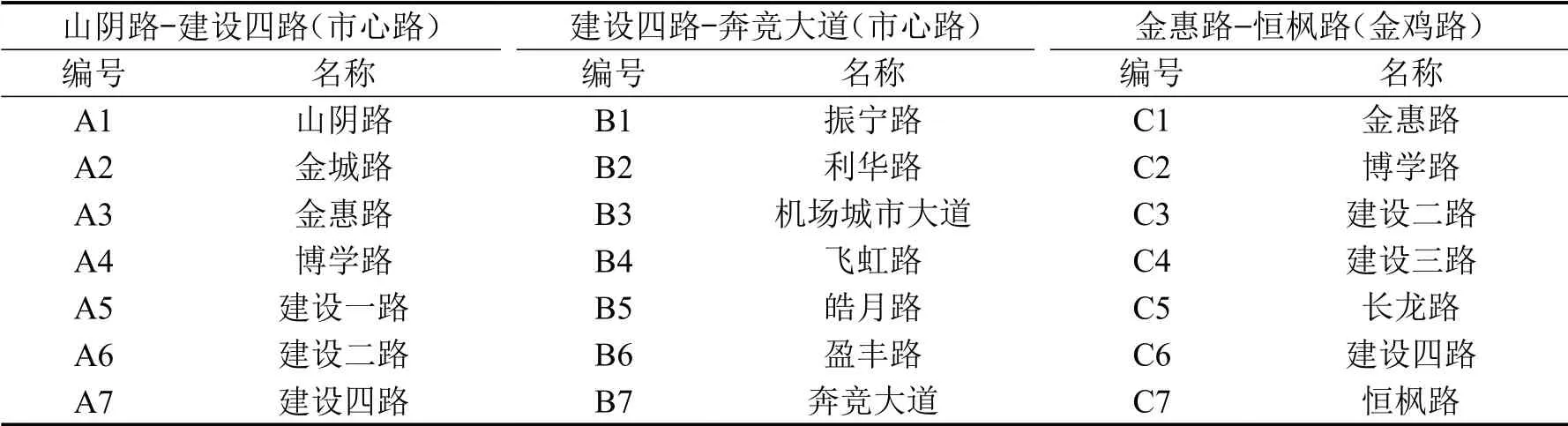
表1 交叉口名称及编号Table 1 Name and number of intersection

图2 交叉口示意图Fig.2 Intersection diagram

选取2019年3月高峰(7:00-9:00)和平峰(13:00-15:00)时段南向北车流的行程时间数据，统计每条路段长度，以及样本量、行程时间的均值、中位数、标准差和变异系数(标准差/均值)，A1-A7路线上各路段的统计结果如表2所示。

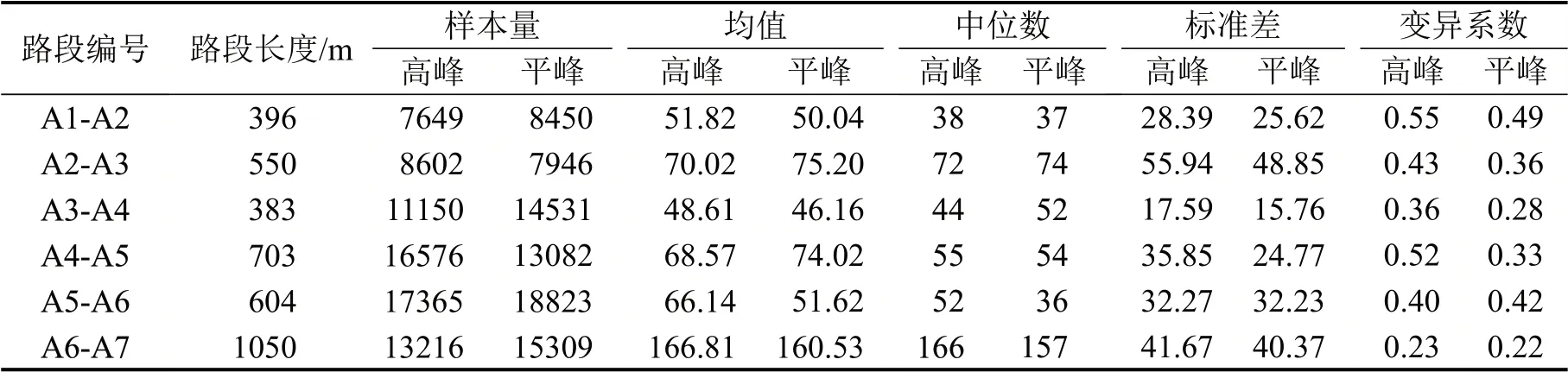
表2 路段统计信息Table 2 Link statistical information

2 路段行程时间特性分析

2.1 行程时间统计分布模型

已有研究表明，行程时间分布往往服从正态、对数正态等单峰分布形式，但观察数据发现，所观察到分布的尾部比正态分布或对数正态分布的尾部更大，且部分路段的行程时间分布具有明显的双峰分布特征，甚至三峰现象。根据相关文献，对单峰分布的行程时间数据，Burr分布可以较好地拟合行程时间分布的右偏且上尾较长的特征[12]，高斯混合分布可以更好地描述多峰现象[5]。

(1)Burr分布

Burr分布作为一种失效模型，广泛地应用于医学、金融和保险等领域，Susilawati[8]将Burr 分布应用于行程时间分布拟合，结果发现，其拟合效果要优于正态分布和对数正态分布。三参数Burr(XII型)分布的概率密度函数表达式为

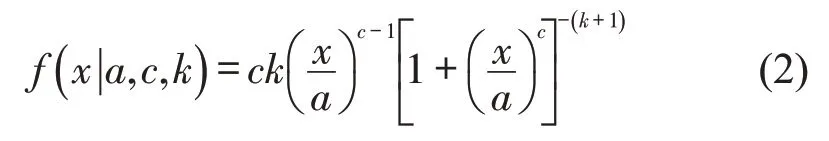
式中：x为随机变量；α为尺度参数；k为形状参数，用于描述曲线的形状变化；c为位置参数，用于描述曲线位置的变化，特别是曲线峰值的位置。

(2)高斯混合模型

高斯混合模型(Gaussian Mixture Model，GMM)是将一个事物分解为若干基于高斯概率密度函数形成的模型。设随机变量x，则高斯混合模型的表达式为

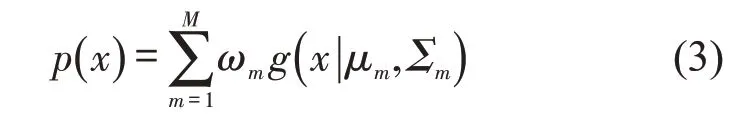
式中：m为高斯混合模型中的成分个数；μm为第m个高斯分布的均值；Σm为第m个高斯分布的协方差；ωm为第m个模型的权重系数，0＜ωm＜1；为第m个高斯成分的分布。

2.2 路段行程时间分布拟合

使用Burr 分布和二元混合高斯分布分别对早高峰和平峰共36 组路段行程时间数据进行拟合，并进行K-S 检验，P值越大，说明分布拟合效果越显著。决策值H=0 表示接受通过检验的假设，H=1表示拒绝通过检验的假设，结果如表3所示。

表3 各路段行程时间分布拟合结果Table 3 Fitting results of travel time distribution of each link

根据拟合结果可知，在显著性水平为0.05 时，36 条路段中只有5 条路段使用Burr 分布拟合通过了显著性检验，接受率为13.89%；而有34条路段使用二元高斯混合分布拟合通过了显著性检验，接受率为94.44%，高斯混合分布较Burr 分布有更好的拟合结果。高峰和平峰时段的路段行程时间分布具有相似特点，车辆由于受到道路线型设计和交叉口信号控制的影响，部分车辆通过交叉口时可能需要经历两个甚至更多的信号周期，使车流出现间断流特征，行程时间分布出现双峰现象，因此高斯混合分布可以更好地描述路段行程时间分布的特征。

2.3 路段长度影响分析

通过相关性分析，路段长度与行程时间均值、中位数、标准差及变异系数之间存在一定的相关性，其相关系数分别为：0.8741、0.8938、0.6034、-0.6076，说明路段长度与行程时间特性之间具有强相关性，路段长度与行程时间均值、中位数和标准差呈正相关关系，与变异系数呈负相关关系。

分析路段行程时间分布特征可以发现，路段长度较短时，由信号控制引起的延误会对路段行程时间造成较大影响，行程时间分布具有明显的双峰现象，虽然行程时间较短，但波动性大。随着路段长度增加，交叉口信号控制延误对路段行程时间的影响减小，行程时间双峰现象减弱，呈现出单峰分布特性，波动性减小。

3 多信号交叉口干线行程时间分布

3.1 干线行程时间分布拟合

3.1.1 拟合结果

分别使用Burr 分布模型和二元高斯混合分布模型对36 组不同干线、不同交叉口数量的数据进行分布拟合及K-S 检验，并通过EM 算法求解二元高斯混合分布拟合参数结果，表4为部分行程时间数据(分别以A1、B1、C1为干线起点)拟合后的K-S检验结果。

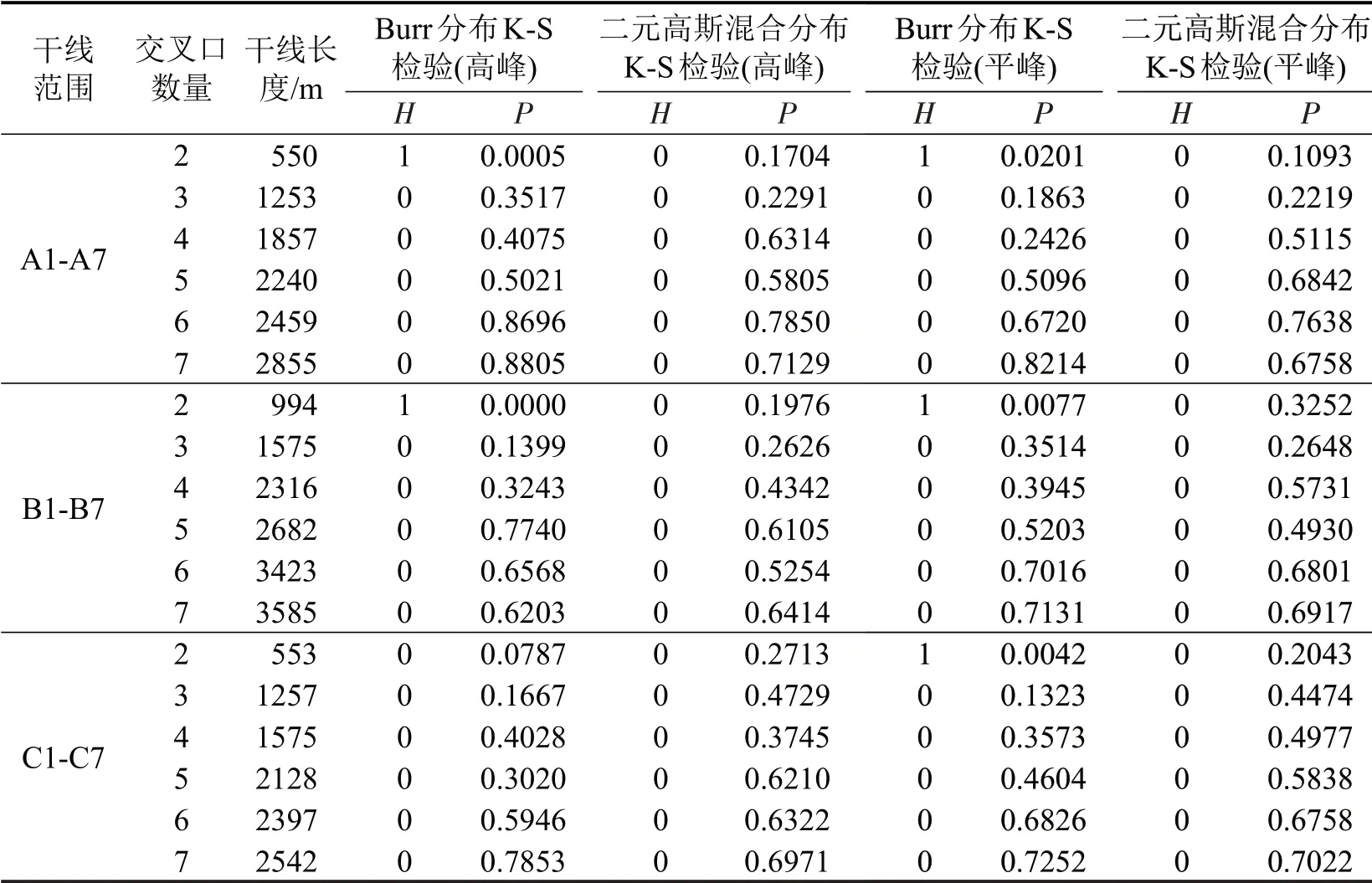
表4 两种分布模型的K-S检验结果Table 4 K-S test results of two distribution models

3.1.2 结果分析

K-S检验得到的P值越大，说明分布拟合结果越好。在显著水平为0.05 时36 组数据中：有31 组数据利用Burr分布拟合的结果通过了显著性检验，接受率为86.11%；有36 组数据利用高斯混合分布拟合结果通过了显著性检验，接受率为100%。对于多信号交叉口干线行程时间数据，无论高峰时段还是平峰时段，高斯混合分布均能通过显著性检验，同时Burr 分布也表现出较好的拟合效果，可以更好地描述行程时间高峰值和右偏的分布特征。

为进一步分析干线行程时间的分布特征，通过EM算法求解各路段行程时间分布的二元高斯混合分布参数，以高峰时段行程时间数据为例，参数如图3所示，图中，ωij表示干线i的二元高斯混合分布拟合模型中第j个高斯分布的占比。观察其权重值可以发现，随着交叉口数量增加，第1 个高斯分布占比达到90%以上，意味着有90%左右的车辆行程时间数据属于第1类，说明该行程时间分布的双峰现象被打破。

图3 二元高斯混合模型参数估计结果Fig.3 Parameter estimation results of Gaussian mixture model

图4 为Burr 分布和二元高斯混合分布的拟合效果图，当交叉口数量较少时，行程时间分布具有不确定性和多峰现象，二元高斯混合分布的拟合效果更佳。随着交叉口数量增加，行程时间趋于一个稳定的单峰分布，此时Burr分布在显著水平为0.05时都能通过显著性检验，且P 值逐渐增大，说明拟合效果越显著。

图4 Burr分布及二元高斯混合分布拟合图Fig.4 Burr distribution and Gaussian mixture distribution fitting diagram

根据分布拟合和参数估计结果，随着交叉口数量和干线长度的增加，交叉口信号控制对行程时间的影响减弱，行程时间分布的双峰现象减弱，第1个高斯分布的权重逐渐增加，行程时间分布表现出长尾右偏形状，从分布直方图中也可以清楚得观察到这一现象。随着交叉口数量和干线长度的增加，两种分布的拟合效果都随之增加，如图5所示，当交叉口数量等于5 且当干线长度约为2500 m 时，Burr 分布的拟合效果与二元高斯混合分布的拟合效果相当。随着交叉口数量和干线长度的继续增加，Burr分布模型可以更好地描述干线行程时间分布特征。

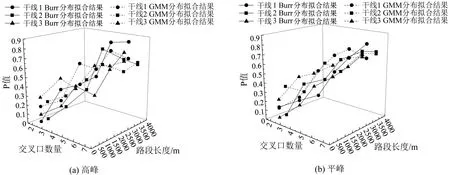
图5 干线行程时间分布与交叉口数量及干线长度关系Fig.5 Relationship between route travel time distribution and number of intersections and route length

3.2 关键影响因素分析

根据上述分析，交叉口数量和干线长度是干线行程时间特性的重要影响因素，此外，干线流量也为行程时间分布的关键影响因素。为进一步分析其相关关系，利用灰色关联分析法分析交叉口数量、干线长度和干线流量与行程时间分布特性及可靠性之间的关系。选取Burr 分布和高斯混合分布的拟合优度来表示行程时间分布特性，以缓冲指数(BI)[13]作为可靠性评价指标。

灰色关联分析法根据因素之间发展趋势的相似或相异程度来衡量因素之间的关联程度，具体步骤如下：

(1)确定参考序列和比较序列。假设评价标准有t个，评价因子有l个，参考序列反应系统行为特征，即，表示第t个评价因子的实测值；比较序列为影响因素数据序列，即，表示第l个评价标准下第t个评价因子的值。

(2)原始数据标准化处理。分析之前，将数据进行无量纲规范化处理，本文采用均值化法，即用各指标的每个值除以其相对应指标的平均值，得到各个指标无量纲的新值。

(3)计算关联系数。即求第l个比较序列与参考序列对应的第t个指标的相对差，计算公式为

(4)计算灰色关联度，即各因子之间的关联程度Rl，计算公式为

以交叉口数量、干线长度、干线流量为原始数据，分别以Burr分布和二元高斯混合分布的拟合优度及缓冲指数为参考序列。利用均值化法对数据进行无量纲处理，再利用式(4)计算关联系数，式(5)计算灰色关联度，结果如表5所示。

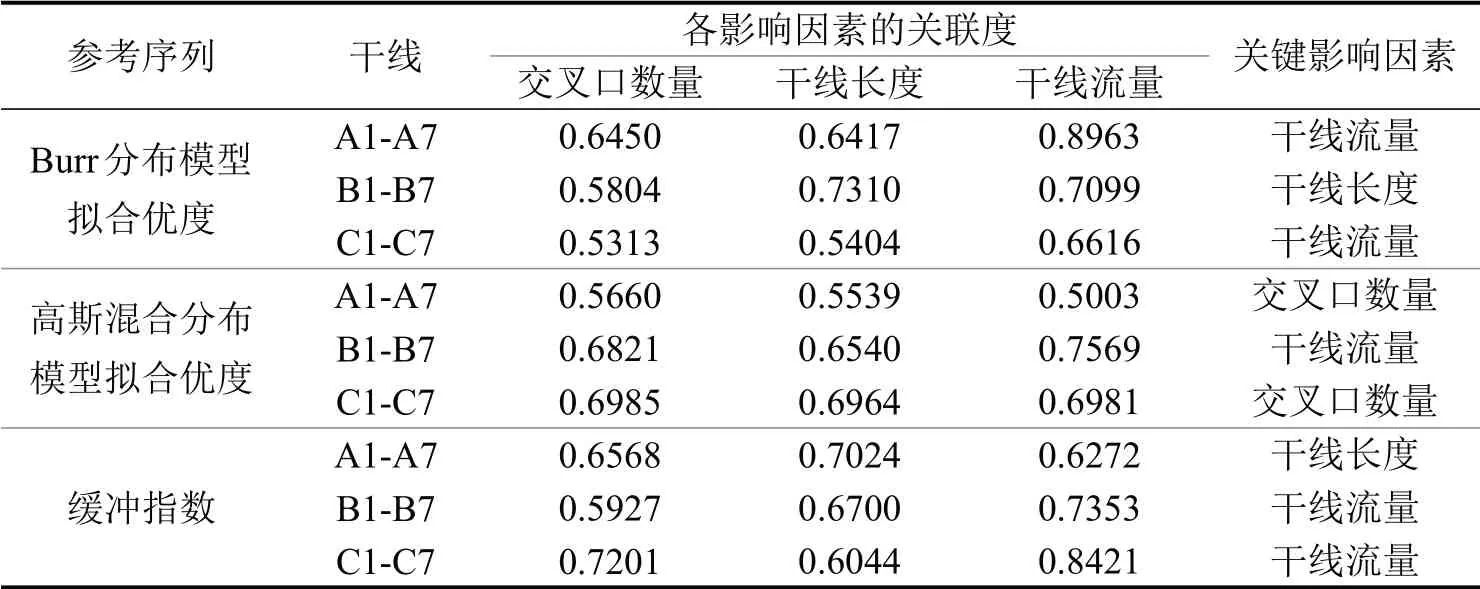
表5 灰色关联分析结果Table 5 Results of grey correlation analysis

以Burr 分布拟合后的P值为参考序列进行分析后发现，干线长度和干线流量与其关联度较高。在灰色系统理论中分辨系数取0.5 时，关联度超过0.6 的影响因子对结果有显著影响，因此干线长度和干线流量对Burr 分布拟合结果有着显著影响。随着干线长度的增加，行程时间趋于一个稳定的单峰分布，Burr 分布可以更好地表示其分布特征，而流量的变化对行程时间的分布特性的影响更为显著。同样的，交叉口数量和干线流量对高斯混合分布的拟合结果有一定的影响，但干线长度和干线流量对缓冲指数的影响更为显著，反映了行程时间可靠性与干线长度呈正比，与干线流量呈反比。

根据以上分析结果，干线长度和干线流量对多信号交叉口干线行程时间有着更为显著的影响，而交叉口数量的影响不显著。由于道路条件差异，不同交叉口之间的间距不同，用交叉口数量来描述行程时间特性时会存在较大的不确定性，特别是当干线上的信号交叉口为协调控制时，由信号控制引起的延误影响减小，交叉口数量与行程时间的相关性也将减弱。

4 结论

本文得到主要结论如下：

(1)单路段行程时间受交叉口信号控制的影响较大，呈现双峰分布现象，二元高斯混合分布表现出较好的拟合效果。对于信号协调控制下的多信号交叉口干线行程时间数据，随着交叉口数量和路线长度的增加，行程时间分布的双峰现象减弱，且表现出长尾右倾特征，此时Burr分布可以较好地描述干线行程时间分布特征。

(2)针对多信号交叉口干线，随着干线长度的增加，行程时间趋于一个稳定单峰分布，Burr 分布拟合K-S检验的P值也逐渐增加，当交叉口数量大于等于6且干线长度大于2500 m时，Burr分布的拟合效果优于二元高斯混合分布，并且波动性减小，行程时间可靠性增加。

(3)交叉口数量、干线长度和干线流量与行程时间特性有着较强的相关性，交叉口数量和干线长度与Burr分布拟合优度和可靠性呈正相关，干线流量与Burr 分布拟合优度和可靠性呈负相关。其中干线长度和干线流量的影响更为显著，而对于信号协调控制的干线，交叉口数量对行程时间特性的影响较弱。

本文分析采用的是信号协调控制下的行程时间数据，尚未对交通信号的影响进行定量分析，在后续研究中将进一步分析信号控制方式、信号配时方案等因素对行程时间特性的影响。