基于激光与视觉融合的车辆自主定位与建图算法

余祖俊，张晨光，郭保青,b

(北京交通大学，a.机械与电子控制工程学院；b.智慧高铁系统前沿科学中心，北京100044)

0 引言

随着计算机技术的快速发展，自主驾驶成为车辆智能化的重要发展趋势，而车辆自身定位与周围环境感知是实现自主驾驶的基础，其准确度和稳定性是智能导航、避障检测、路径规划和车辆控制[1]的基本保障，对提升自主驾驶车辆的安全性有至关重要的作用。

传统的车辆定位技术大多需要借助GPS/INS组合系统[2-3]来实现，但是GPS系统存在信号不稳定的缺陷，在城市高楼或隧道等信号遮挡的地点常会失效，此外，GPS 还存在地图版本与实际路况不匹配的情况。INS(Inertial Navigation System)惯导系统由于陀螺仪零点漂移严重和车辆震动等因素，无法通过直接积分加速度获得高精度的方位和速度等信息，需要定期纠正累积误差。SLAM(Simultaneous Localization And Mapping)，即时定位与地图构建，近年来被更多地用于自主驾驶定位模块，其相关算法研究经历了30多年的发展，所使用的传感方式主要分为激光和视觉两类。早期的激光SLAM 算法多以2D 激光雷达配合滤波算法为主，主要包括：卡尔曼滤波和粒子滤波。后期随着硬件技术的发展和图优化理论的健全，3D 激光雷达配合优化算法成为新的主流方式，ZHANG 等[4]提出的LOAM(Lidar Odometry and Mapping)算法将SLAM 问题分为高频率、低精度的里程计问题和高精度、低频率的建图问题。JI等[5]提出的LLOAM(Lidar Odometry and Mapping with Loopclosure Detection)算法在LOAM 的基础上添加了基于点云分割匹配的回环检测和基于图优化的后端，建立了完整的3D 激光SLAM 算法框架。SHAN 等[6]根据LOAM 提出一种轻量级的激光雷达测程法LeGO-LOAM(Lightweight and Ground-Optimized LOAM)，应用点云分割对地面点进行优化处理并且滤除大量的噪声点，将位姿分为两类分别估计。然而，上述算法存在计算量过大，无法长时间运行的问题。

以视觉作为主要观测手段的SLAM 算法通常被称为视觉同步定位和绘图VSLAM(Visual Simultaneous Localization and Mapping)，其发展类似于激光SLAM，经历了卡尔曼滤波到粒子滤波再到图优化的过程。西班牙的RAUL等[7]提出的ORB-SLAM2 基于PTAM(Parallel Tracking and Mapping)进行改进，该算法基于ORB 特征点，将算法分为追踪、局部建图及回环检测3部分。德国的ENGEL 等[8]提出的LSD-SLAM(Large-scale Direct SLAM)是一种在高梯度图像区域最小化光度误差的半感知直接算法。瑞士的FORSTER 等[9]提出介于直接法和特征法之间的半直接视觉测程SVO(Semi-direct Visual Odometry)。上述视觉SLAM 算法由于视觉捕获信息时易受光照影响的缺陷而存在定位漂移的问题。

近年，融合激光雷达和单目相机的SLAM算法采用紧耦合的模式框架备受关注，ZHANG 等[10]提出一个融合激光雷达、相机和惯导的算法V-LOAM(Visual-Lidar Odometry and Mapping)，其各个模块采用紧耦合的运作方式，并且运动模型采用等速度高斯过程，测程的精度极高。在V-LOAM 的基础上，ZHANG 等[11]提出一个在线处理运动数据算法LVIO(Laser-Visual-Inertial Odometry)，该算法利用来自3D 激光雷达、相机和惯性测量单元的数据构建大范围环境地图。与使用卡尔曼滤波或因子图优化的传统方法不同，该算法采用顺序的、多层处理线程，从粗到细求解运动。然而，上述融合算法主要针对提升算法精确性进行设计，计算量巨大。本文参照LVIO 的算法框架并对其进行轻量化改进，提升在精确性、鲁棒性和资源占用率方面的整体表现。

1 问题描述与建模

为描述SLAM 问题，首先，将车辆在一段连续时间的运动分解成离散时刻t=1,…,k时刻的运动，这些时刻的位置x1,x2,…,xk构成车辆的运动轨迹。然后，设地图由许多特征点组成，每个时刻传感器会测量到一部分特征点，得到它们的观测数据，设特征点有n个，为y1,…,yn。不管是激光雷达还是相机，运动方程的数学模型为

式中：f(·)为运动方程函数；uk为运动传感器的读数；wk为噪声。与运动方程相对应，观测方程为

式中：h(·)为观测方程函数；vk,j为观测噪声；观测方程描述的是当车辆在xk位置上提取到第j个特征点yj，产生了一个观测数据zk,j。

运动方程和观测方程描述了最基本的SLAM问题，即知道运动测量的读数u，以及传感器的读数z时，如何求解定位问题(估计x)和建图问题(估计y)。此时，SLAM 问题就被建模成一个状态估计问题。

考虑到车辆行驶所处的复杂环境，运动和观测方程通常为非线性，噪声分布通常为非高斯分布。面对复杂的非线性系统，主流SLAM一般使用以图优化(Graph Optimization)为代表的非线性优化技术进行状态估计，其中，光束平差法(Bundle Adjustment，BA)是一种性能优良的非线性优化方法，本文采用基于BA 的图优化方式估计系统位姿和特征。

本文算法用到的坐标系包括：激光雷达坐标系{ }L，相机坐标系{ }C和世界坐标系{ }W。首先，相机的内参矩阵和激光雷达相对于相机的位姿矩阵都可通过联合标定获得。然后，将激光雷达获取的数据从{ }L投影到{ }C下，即可以{ }C代表车辆整体的坐标系{ }S，以车辆初始时刻的{ }S作为{W}。算法坐标系如图1所示，其中，X，Y，Z轴的轴向分别为车辆的正左方，正上方和正前方。车辆的坐标系随着车辆的移动而变化，因此，用Sk表示车辆在时刻k的坐标系。

图1 算法坐标系示意Fig.1 Schematic diagram of algorithm coordinate system

2 算法求解

2.1 算法总体框架

结合算法的需求分析和相关理论知识，本文提出一种基于激光视觉融合的车辆自主定位建图SLAM算法，分为前端里程计和后端非线性优化两部分。

对于前端里程计部分：首先，分别从预处理后的雷达和相机数据中提取ORB特征点和点云边缘平面特征点，并分别对其进行帧间匹配；然后，利用对应的雷达帧的点云以三角面投影的方式获取ORB特征点深度得到Space-ORB，再将其和雷达特征点以松耦合的方式输入到位姿估计模块，输出初始位姿。

在后端非线性优化部分：利用得到的初步估计位姿将特征点映射到世界坐标系下，并输入到全局优化模块，通过关键帧和滑动窗口的平衡选取策略，以及分类优化策略对初始位姿和特征点进一步优化；同时，利用基于激光点云的ICP(Iterative Closest Point)修正法和基于ORB 特征点的视觉词袋模型执行回环检测；最终，输出优化后的6 自由度位姿和点云地图。算法整体框架如图2所示。

图2 算法整体框架Fig.2 Overall framework of algorithm

2.2 基于点云构建Space-ORB视觉特征点

ORB 特征点没有深度信息将会导致位姿估计时存在尺度偏差，故基于ORB 的扩展提出Space-ORB。对连续帧中可以互相匹配的ORB 特征点，利用三角面投影的方法获取该点的深度。将相机像素平面C上的ORB特征点pc和{ }S的Z轴正向的空间雷达点全部按照比例投影到{ }S的Z轴正向10 m处的平面K上，得到视觉映射点和雷达映射点pl。之后，在K上对每个通过k-d 树搜索算法在雷达映射点中找到距离其最近的3 个点，再以这3个点所对应原始雷达点,构建一个三角形平面T，将投影到T上得到，则被估计为环境中ORB特征点pc的真实位置，获取到该点的深度信息，即获得了Space-ORB。视觉特征点获取深度如图3所示。

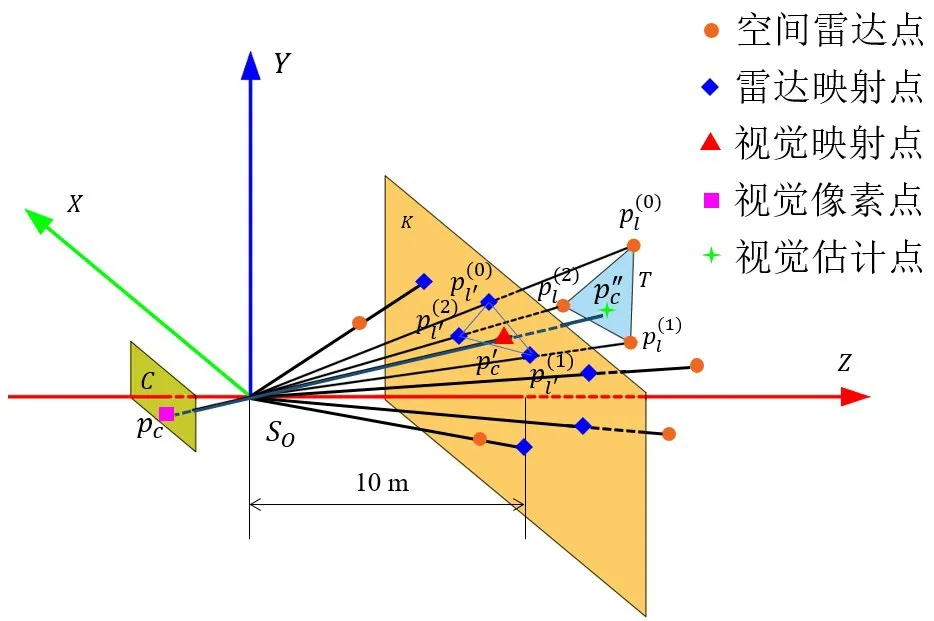
图3 视觉特征点获取深度示意Fig.3 Visual feature points to acquire depth schematic

2.3 基于松耦合的激光视觉融合位姿估计

传感器在k与k-1 时刻获取到的激光和视觉特征匹配点在前、后两帧整体坐标系下的齐次坐标和前、后两帧的位姿变换矩阵满足关系，即

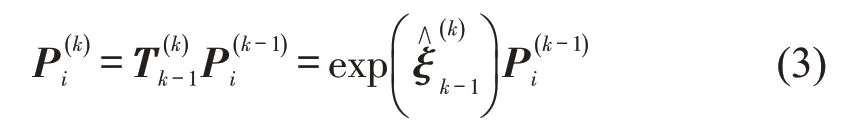
为保证所有匹配点在前、后帧中的总误差最小，构造位姿优化函数，求使前、后两帧中各匹配点的位姿误差对应的二范数平方总和最小的6维向量。

在构建无约束优化模型并得到导数矩阵后，即可利用Levenberg-Marquardt(L-M)法进行目标优化函数的迭代求解，在达到设定的迭代次数或者精度之后，停止迭代，得到初步估计的局部位姿。

式(4)的位姿优化函数以误差项的二范数平方总和最小为目标函数，但在SLAM算法中存在误匹配特征点会使对应的误差项严重偏大，进而导致其梯度也很大，即算法将花费大量的计算量用于调整一个错误的值。该问题的根源是二范数平方的增长速率过快造成的。为此，将式(4)中的匹配点误差项代入Cauchy核函数，由于Cauchy核函数采用了对数操作，当个别误匹配点引起误差项过大时目标优化函数值也不至于过大，可以实现异常值的抑制，即

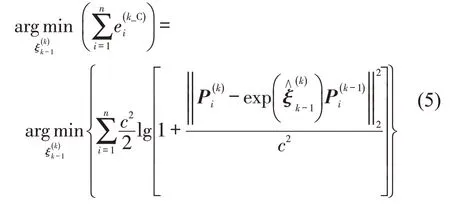
为进一步降低误匹配点造成的误差项，在Cauchy 误差项基础上提出Cauchy-Huber 误差度量函数。当匹配点的Cauchy 误差项较小时，Huber函数仍保持原来的度量函数；当较大时，Huber 函数将原来的二次函数变为线性函数，可降低误匹配点的影响，提升算法对异常值的泛化性和位姿优化求导时的平滑性。

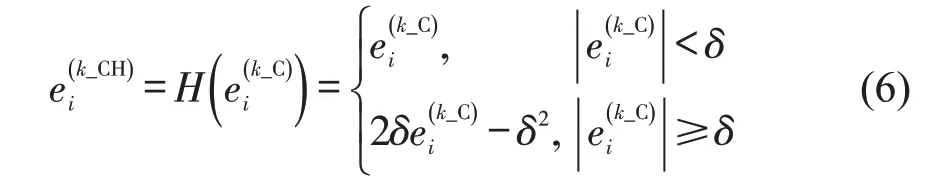
式中：δ为所有匹配点误差项的标准差。

2.4 基于关键帧和滑动窗口的平衡选取策略

同时优化过去所有位姿和数据点会导致计算量过大，并且误差通常都是局部存在的，针对此问题，某些SLAM算法采用选取关键帧加滑动窗口的方式进行全局优化。但是其选取关键帧的频率和滑动窗口的长度是固定的，导致泛化性较差。本文对关键帧的位置和滑动窗口长度的选取提出一种平衡选取策略，如图4所示。图中，矩形框为滑动窗口，包含待优化的数据帧。

图4 基于关键帧和滑动窗口的位姿优化Fig.4 Pose optimization based on keyframe and sliding window

如图4中圆圈内的数字所示，关键帧的选择策略是先将所有的数据帧分为3类：可以直接用于稳定优化的帧，无用信息过多不应使用的帧，可以使用但需要处理减少计算成本的帧。第1 类是会影响关键测量的帧，在一些快速变换的场景下，例如，大幅度转弯处，此时特征匹配难度增加，需要增加关键帧的密度。第2 类是当车辆自身相对道路静止时，周遭场景内可能会有其他的动态物体干扰车辆姿态估计，此时，需要设定动态特征点的数量阈值，在低于阈值时，不选取任何关键帧。第3 类是余下一般情况的帧。提取关键帧的频率fk为

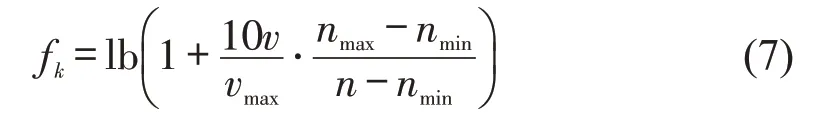
式中：n为可连续追踪特征点的数量；nmax、nmin分别为最大值、最小值；v为车辆速度；vmax为最大车速。

为保证满足优化精度的同时计算量也尽可能小，提出平衡选取公式来决定优化窗口的长度lw，即

当前关键帧和窗口最新的关键帧进行特征点的匹配计算，小于某个阈值时就把当前关键帧纳入优化窗口作为最新的关键帧，同时长度l本身有最大lmax和最小lmin的限制值。

2.5 基于特征点和位姿的分类优化策略

为更有效率的后端优化，特征点的选取也极为重要。特征点本身应当具有良好的观测性，无异常值，并且在3 维空间中均匀分布，便于后续的建图工作。本文设置阈值df，以激光雷达的最大探测范围将车辆附近区域分成远近2 个区域；将Space-ORB，边缘激光点，平面激光点分为远近2类，即激光和视觉特征点分为6类。

由于特征点距离车辆的远、近对运动姿态估计中的平移误差和旋转误差有不同的影响，近点对于平移估计影响较大，远点对于旋转估计影响较大。除此之外，在车辆的6自由度位姿估计中，X、Z 平面下的位置和偏航角β的精确度更为重要。因此，将位姿李代数分为ξX,Z,ξβ,ξY和ξα,γ4 类，令不同类的点分别对不同的位姿进行优化，如图5所示。

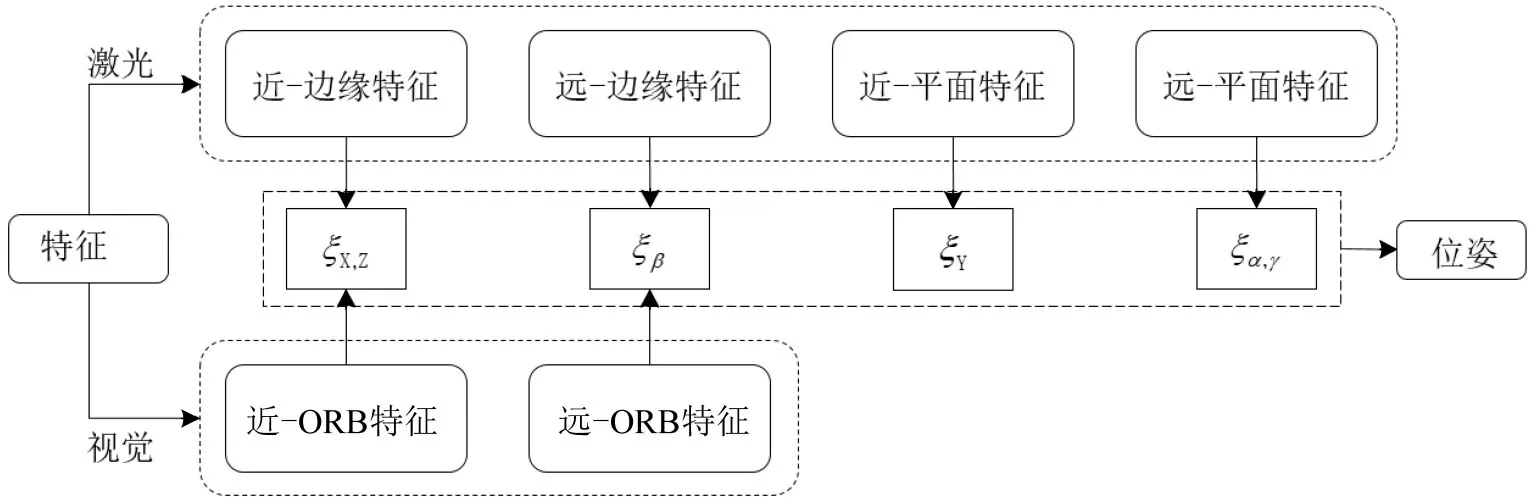
图5 特征点和位姿分类的优化策略Fig.5 Optimization strategy for feature points and pose classification

2.6 基于点云ICP算法的回环检测模块设计

回环检测，主要解决位置估计随时间漂移的问题。通过检测机制，判断车辆当前所处位置与之前到过的位置的场景相似性，在检测出回环后，通过优化手段，将偏移值消除，完成回环检测。本文参考LeGO-LOAM[6]算法中的回环检测模块并对其加以改进，添加了一个位姿距离约束条件以提升其检测率。

首先，要对是否存在回环进行判断。设当前帧激光特征点云为Pinput，对半径为r的圆形范围内进行位姿距离检测，这里要排除当前帧前t秒内的帧，将检测到的与当前位姿距离小于r的目标帧点云投影到世界坐标系下作为待检测点云Ptarget。然后对Pinput和Ptarget执行ICP 算法，在满足迭代次数并且噪声分数较低的条件下，输出位姿向量ft，此时，即认为检测到了回环。

得到ft后，可算出被检测到的位姿在历史位姿帧中的位置kl。最后，对第ks帧和第kl帧之间的车辆位姿进行优化修正，通过加上第ks帧和第kl帧位姿的额外约束，将其代入到全局优化函数中。最终输出修正后的位姿轨迹和点云地图，即优化帧。回环检测流程如图6所示。

图6 回环检测流程Fig.6 Loop detection flow chart

3 实验与结果分析

3.1 算法鲁棒性实验

本文实验选取KITTI[12]数据集的Odometry 场景合集作为测试对象。该数据集包含了标注真值和未标注真值的各11 个场景的真实数据序列，涵盖郊区公路、高速公路、城市道路等各类典型道路场景，视觉测距序列涵盖39.2 km的道路场景，每个场景数据包含：图像、激光雷达点云及真实位姿的数据序列，是测试定位建图算法通用的数据集。关于鲁棒性的第1 个实验是通过算法提取的特征点个数检验其对不同环境的适应能力。具体来说，分别检测不同环境下本文融合算法所提取的视觉特征点和激光雷达特征点的数量，并将结果与激光算法A-LOAM 和视觉算法ORB-SLAM2(Mono)进行比较。为更直观地比较3 种算法在不同场景下提取特征的差异，本文将每种算法在各个场景下的特征提取数占所有场景总特征提取数的百分比绘制成条状对比图，如图7所示。

图7 各算法提取的特征点个数占其总数的百分比Fig.7 Percentage of number of feature points extracted by each algorithm in total

由图7可知，在以郊区为主要场景的环境(场景3、场景4)和高速公路(场景1)中，视觉特征点较少，激光雷达特征点较多，这将影响到单以视觉特征点作为运动先验的ORB-SLAM2(Mono)算法后续位姿估计的计算。在以城市为主要场景的环境(场景0、场景5、场景6、场景7)中，激光雷达特征点较少，而视觉特征点较多，这将影响到单以激光雷达特征点作为运动先验的A-LOAM算法后续位姿估计的计算。融合算法同时接受视觉和激光雷达特征点作为运动先验，因此，从每个场景中提取的特征点总量相对平均，这也证明了该算法在不同环境下具有较好的鲁棒性。

测试算法鲁棒性的第2 个实验是在各个场景下以每隔100 m 为节点，取前800 m 的平均平移误差和旋转误差。由图8(a)和图8(b)可知，A-LOAM算法的平移误差随长度的增加而增大，这是因为该算法没有回环检测，导致路径过长时漂移严重。相比之下，本文融合算法和ORB-SLAM2(Mono)的平移误差和旋转误差随长度的增加而较为平稳的下降。此外，还测试了算法在不同车速下的误差。由图8(c)和图8(d)可以看出，ORB-SLAM2(Mono)在车速变化时引起的误差变化较大，而融合算法和A-LOAM的误差变化较为稳定。

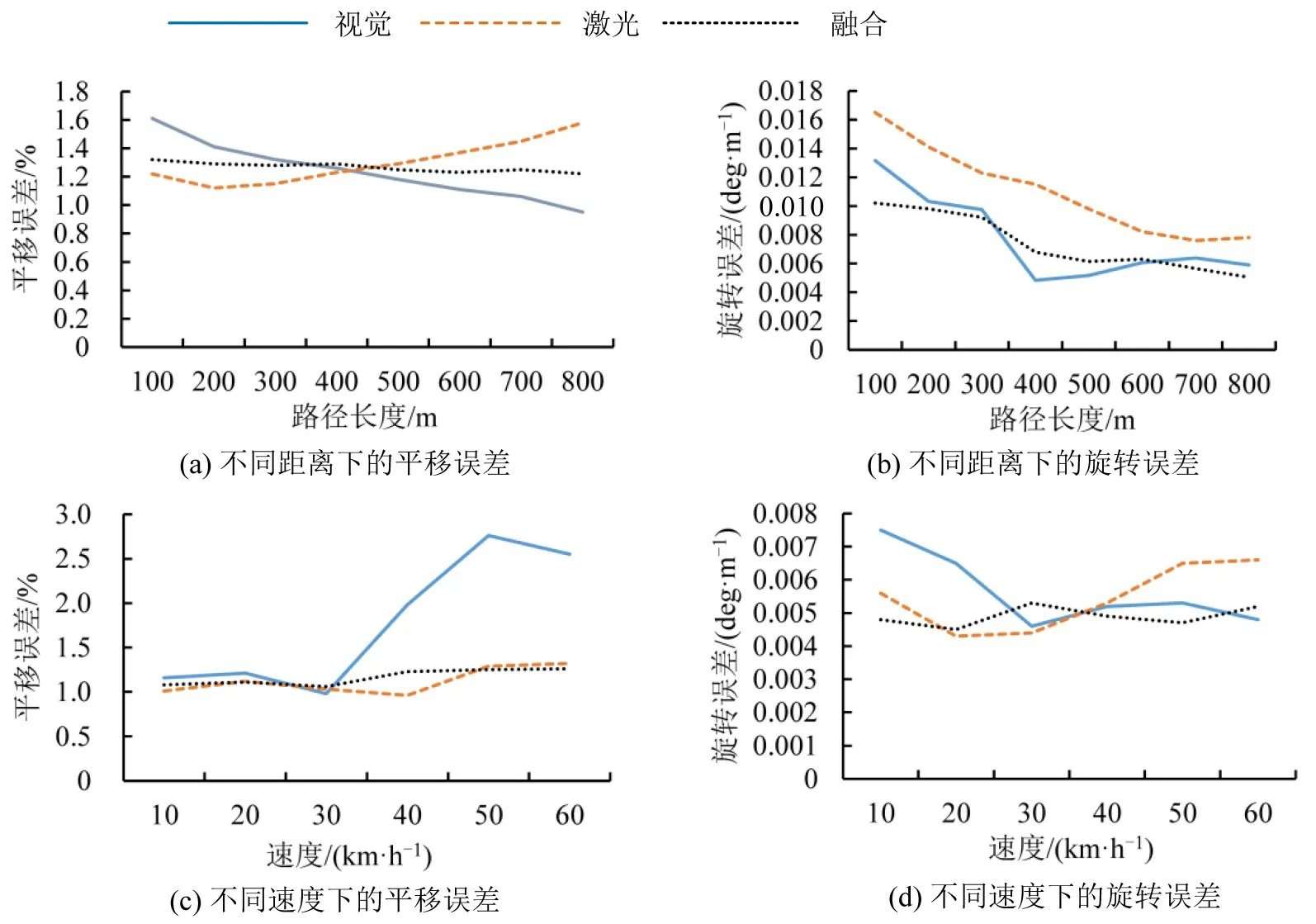
图8 所有场景的平均平移和旋转误差Fig.8 Average translation and rotation errors for all scenarios

综上可知，融合算法在不同的环境下具有较好的适应能力，且稳定性较强，面对不同的车速变化具有更强的抗干扰能力，算法鲁棒性较高。

3.2 算法精确性实验

本文对算法的精确性评估是通过计算位姿轨迹与地面真实轨迹之间的绝对误差APE(Absolute Pose Error)和相对误差RPE(Relative Pose Error)实现的。APE 指两个轨迹上相应位姿之间的欧式距离，反映算法整体的精确性；RPE 指两个轨迹上相应的相邻位姿之差的欧式距离，反映算法局部的精确性。本文在Odometry00～Odometry10 共11 个场景下分别运行3个算法，将输出位姿分别与真实轨迹比较计算APE 和RPE，并输出标准差、均方根误差及均值。各算法在11个场景下的输出误差值取平均值并构建条状对比图，如图9所示。

由图9 可知，相比于另外两种算法，ORBSLAM2(Mono)算法在4 类误差中表现较差。在绝对平移和旋转误差方面，融合算法的各项误差值均略低于A-LOAM，均值达到了28.47 m 和0.03 rad。而在相对旋转误差方面，融合算法各项误差值远低于A-LOAM，均值达到了0.11 m 和0.002 rad。因此，与另外两种算法相比，融合算法综合精确度误差最小。

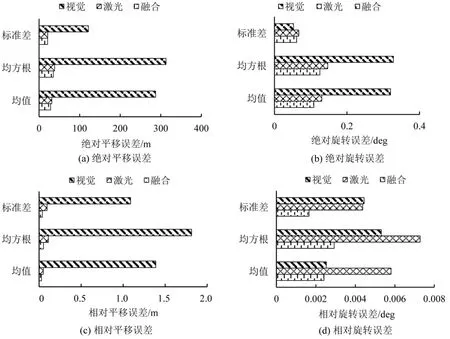
图9 各算法在所有场景下的平均误差Fig.9 Average error of each algorithm in all scenarios

3.3 回环检测实验

本文将融合算法与Lego-loam[6]进行回环检测模块的实验比对，以Odometry 中的Sequence05 作为测试场景，该场景拥有较多的回环部分。算法输出的地图主要为道路和两侧的边缘特征，包括算法输出的车辆运行轨迹。回环检测效果如图10所示。

图10(a)为Lego-loam 输出的轨迹和点云地图中未能检测出回环的路段截取，可以看出，道路的边缘位置点云发生了重影现象，算法在所示路段未能很好检测到回环导致其所构建的地图在同一地方出现了2 条重合的街道。针对相同的路段，图10(b)为本文融合算法的运行结果，街道及其边缘特征点云分布清晰，不存在交叉模糊的情况，成功检测到回环并进行了修正。

图10 回环检测效果对比Fig.10 Comparison of loop detection effect

因此，本文算法对Lego-loam 的回环检测模块进行改进后，检测率得到提升，车辆轨迹和地图点云漂移现象有明显改善。

3.4 资源占用率测试实验

自动驾驶系统除了定位模块之外，还需配有目标检测，路径规划等模块。因此，在有限的计算资源下，应当尽可能地缩小算法的计算量，同时也要保证算法的性能。 本文对3 种算法在sequence00～sequence10 各个环境下运行时计算机的CPU(I7-7700HQ，2.80G HZ×4)和内存(16 G)平均占用率进行了测试和对比。测试方法是运行时每5 s 记录1 次CPU 和内存的占用率，然后取平均值。算法CPU占用率如表1所示，算法内存占用率如表2所示。

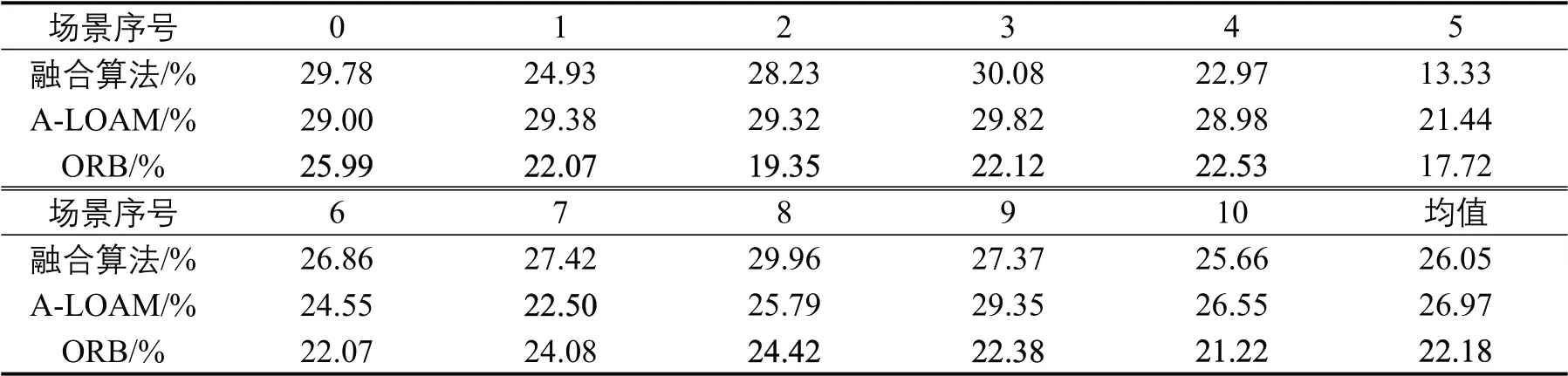
表1 算法CPU占用率比较表Table 1 Comparison of CPU occupancy of algorithms

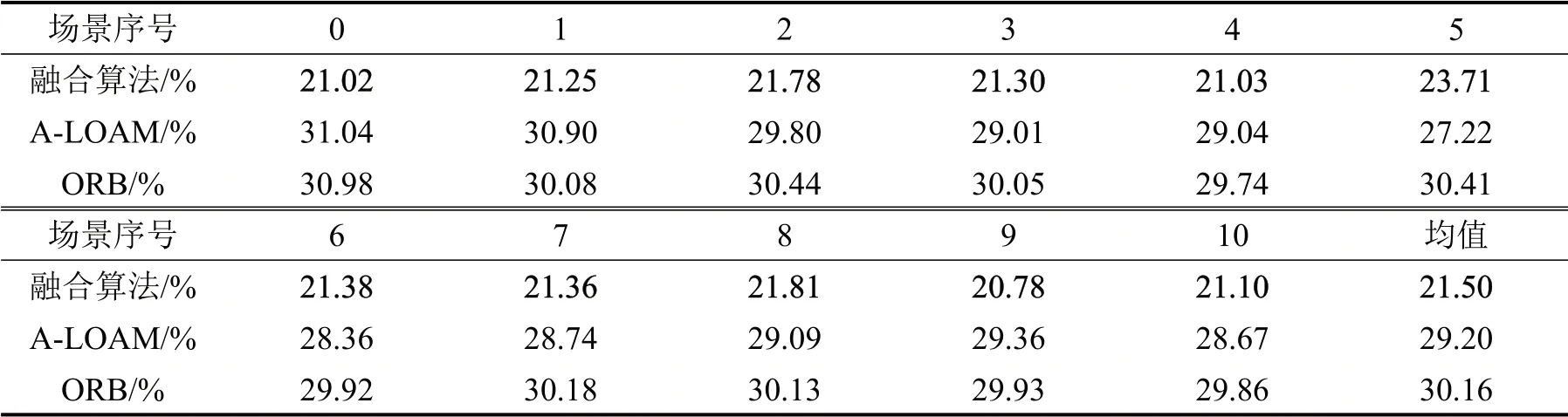
表2 算法内存占用率比较表Table 2 Comparison of memory occupancy of algorithms

表格的最后1列为3种算法在所有场景下的占用率数值再取平均值。从平均值中可以看出，本文融合算法的CPU 平均占用率为22.18%，介于其他两种算法之间，但其内存平均占用率为21.50%，远低于其他两种算法。这是由于本文算法提取特征点总量较少，且后端的优化策略减少了计算量。综合前文的算法性能测试来看，本文提出的融合算法资源占用率更少，而准确度和鲁棒性更高，适用于车辆自主驾驶系统的定位。

3.5 校园环境实车实验

除了数据集外，本文还利用前文所述的硬件和软件平台进行实车实验，车辆行驶环境为校园内部，多为教学楼和植被。通过布置在车上的激光雷达和相机，对车辆周围的环境进行信息采集，同时，利用算法对车辆进行定位并对校园环境构建3 维点云地图。

利用上述算法在北京交通大学主校区内大范围的运行效果如图11所示，其中，图11(a)为主校区内的点云地图以及车辆轨迹；图11(b)为卫星鸟瞰图下的主校区。本次实验全程路径约3 km，局部存在部分小型回环，整体为大型回环。从图11(a)中可以看出，车辆行驶路径周围环境的点云地图构建较为清晰，在各个局部小回环和大型回环处均能成功检出并修正漂移。将图11(a)与图11(b)进行比较可以看出，算法在大范围场景下最终生成的地图构建良好，车辆轨迹无明显漂移现象。因此，算法在小范围和大范围场景下均有良好的表现，实车实验较为成功。

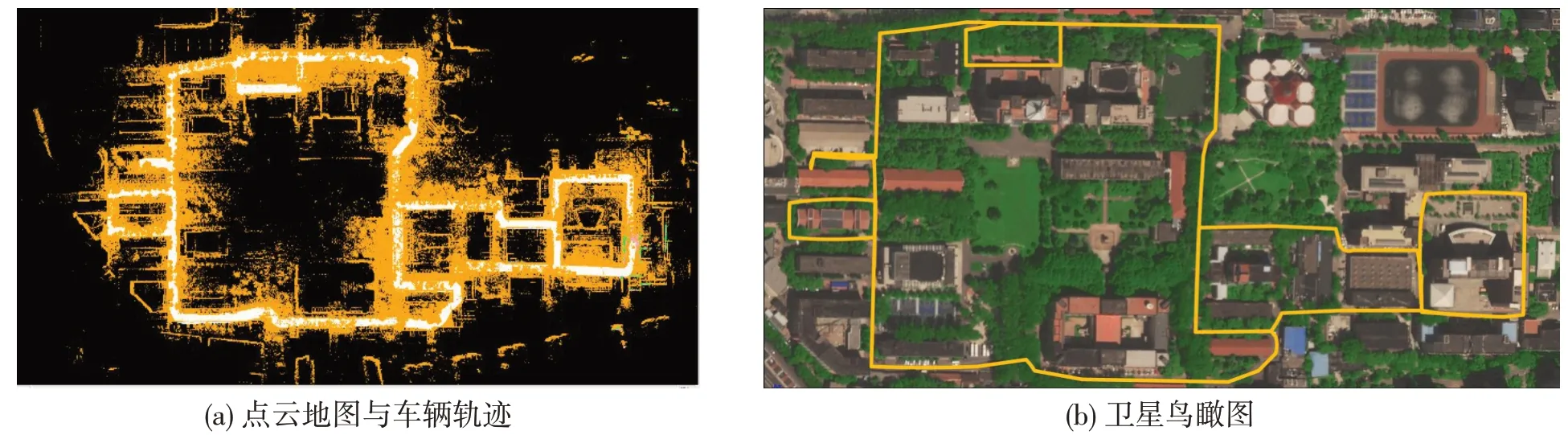
图11 北京交通大学主校区建图与车辆轨迹Fig.11 Building map and vehicle track of main campus of Beijing Jiaotong University

4 结论

本文提出一种基于激光与视觉融合SLAM 的车辆自主定位算法。KITTI 数据集及校园实车实验表明，本文算法在车辆不同行驶距离和不同车速下具有稳定的定位精度，且在各场景下的特征点总数趋于稳定，具有良好的鲁棒性。与其他两种经典算法相比，本文算法在精确性、鲁棒性和资源占用率上均有良好表现。算法平均定位相对误差为0.11 m 和0.002 rad，综合精确度最高；CPU 平均占用率为22.18%，介于其他两种算法之间；内存平均占用率为21.50%，远低于其他两种算法。