几种波动方程叠前深度偏移方法对比研究
张向辉,庞 涛,李 江
(1.陕西延长石油(集团)有限责任公司,陕西 延安 716000; 2.中煤科工集团西安研究院有限公司,陕西 西安 710077)
波动方程叠前深度偏移方法由于其先进的理论基础和在复杂区精确的成像效果,近年来得到广泛的研究发展与应用。波动方程叠前深度偏移的技术核心是地震波场的延拓算法,不同的波场延拓方法构成了不同的偏移方法。目前主要的波场延拓方法有有限差分方法和基于傅里叶变换的频率波数域方法。Claerbout等[1-2]将波动方程有限差分方法(FD)应用于地震叠后偏移,为FD方法奠定了理论基础。差分网格和计算步长是影响该有限差分偏移方法精度和效率的关键因素;另外,受地下反射界面倾角限制,有限差分方法易产生波形畸变现象[3-5]。高阶有限差分可以消除复杂构造区的频散现象,但其计算量较大[6]。为了提高计算效率,马在田等[7-8]提出了有限差分高阶方程的降阶算法;Gazdag等[9-10]提出了相移偏移算法,该方法通过傅里叶变换在F-K域进行波场延拓与成像,大大提高了波动方程叠前深度偏移的计算效率,但该方法基于层状介质假设,仅适应于速度垂向变化;Gazdag等[11]发展了相移加插值的波场延拓方法来适应速度的横向变化;Stoffa等[12]提出了分步傅立叶方法,一定程度上适应了速度的横向变化;Ristow等[13]提出了傅立叶有限差分偏移算法;Wu Rushan[14]提出了广义屏波场方法。这些方法均在SSF方法的基础上针对速度横向变化引起的二阶以上扰动波场进行求解,实现地震波场在复杂介质中的传播模拟[15-16]。
本文从叠前深度偏移的基本原理出发,介绍了FD、PS、SSF、FFD等几种波场延拓算法,分析了存在速度误差时SSF、FFD方法的相对误差,并通过模型测试对几种方法进行成像效果对比,分析了各种方法的特点及适用性,为实际应用中叠前深度偏移方法的选择提供依据。
1 方法原理
1.1 有限差分法
实际应用较广泛的是45°有限差分方程,即:
(1)
式中,P为波场函数;V为地震波速度;t为地震波旅行时间;z为深度;x为炮检距。
由于地震波传播过程中的能量衰减,可以认为在一定的距离之外地震波场能量为0,利用边界条件、初始条件、波场延拓及成像条件,即可求出地下反射界面P(x,z,t=0)。
1.2 相移方法
时间—空间域二维声波方程可表示为:
(2)
相移法偏移的波场延拓算子可表示为:
(3)
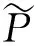
1.3 分步傅里叶方法
对于横向变速介质,依据速度分裂的思路可以将复杂速度场分解为匀速背景场和变速扰动场2部分,对应的慢度场也相应地分为2部分:
S(x,z)=S0(x,z)+ΔS(x,z)
(4)
式中,S(x,z)为介质慢度;S0(x,z)为背景慢度;ΔS(x,z)为扰动慢度。
据此,波场可依据慢度分成背景波场和扰动波场2部分:
P(x,z;ω)=P0(x,z;ω)+PS(x,z;ω)
(5)

(6)
(7)
式(6)、(7)构成分布傅里叶偏移的波场延拓公式。
1.4 傅里叶有限差分方法
FFD偏移方法的波场延拓分为3步来完成[17]。
(1)第1步,F-K域相移处理:
(8)
(2)第2步,频率—空间域基于速度扰动的时移校正:
(9)
(3)第3步,频率—空间域基于速度高阶扰动的有限差分处理:
(10)
式中,a1=2.0;b1=(1+p+p2)/2;p=c/v;c为常数,表示横向均匀速度。
2 方法对比
2.1 算法误差分析
在F-K域,波场传播的频散关系方程的相对误差表示为[18]:
(11)
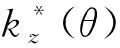
(12)
FFD波场延拓算法相对误差为:
(13)
式中,r2=sin2θ。


图1 偏移算子相对误差曲线Fig.1 The relative error of migration operator
2.2 偏移效果测试
设计如图2所示的4层介质模型进行成像效果测试,正演模拟获得该模型不同位置的地震单炮记录如图3所示,可以看到模拟数据中有直达波、反射波和断点绕射波。几种叠前深度偏移方法的成像效果如图4所示,各种方法均获得模型的基本构造特征,但FD方法网格频散现象严重,出现较明显的高频背景噪音。相移偏移对水平界面成像较好,但对起伏界面成像分辨率较低。分步傅里叶偏移方法对水平界面、起伏界面和深部断层构造均取得较好的成像效果,傅里叶有限差分方法进一步提高了复杂速度结构区域的成像精度,相比其他几种偏移方法取得了最好的成像效果。
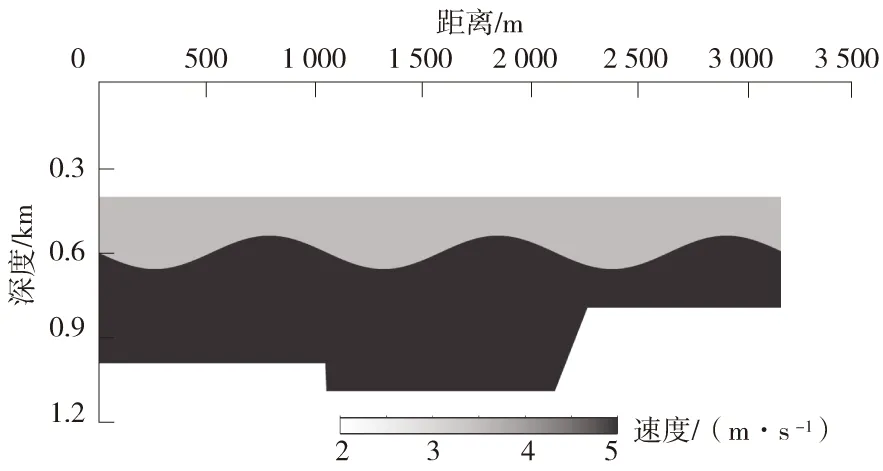
图2 测试模型速度剖面Fig.2 Velocity section of test model

图3 正演模拟记录Fig.3 Forward simulation records
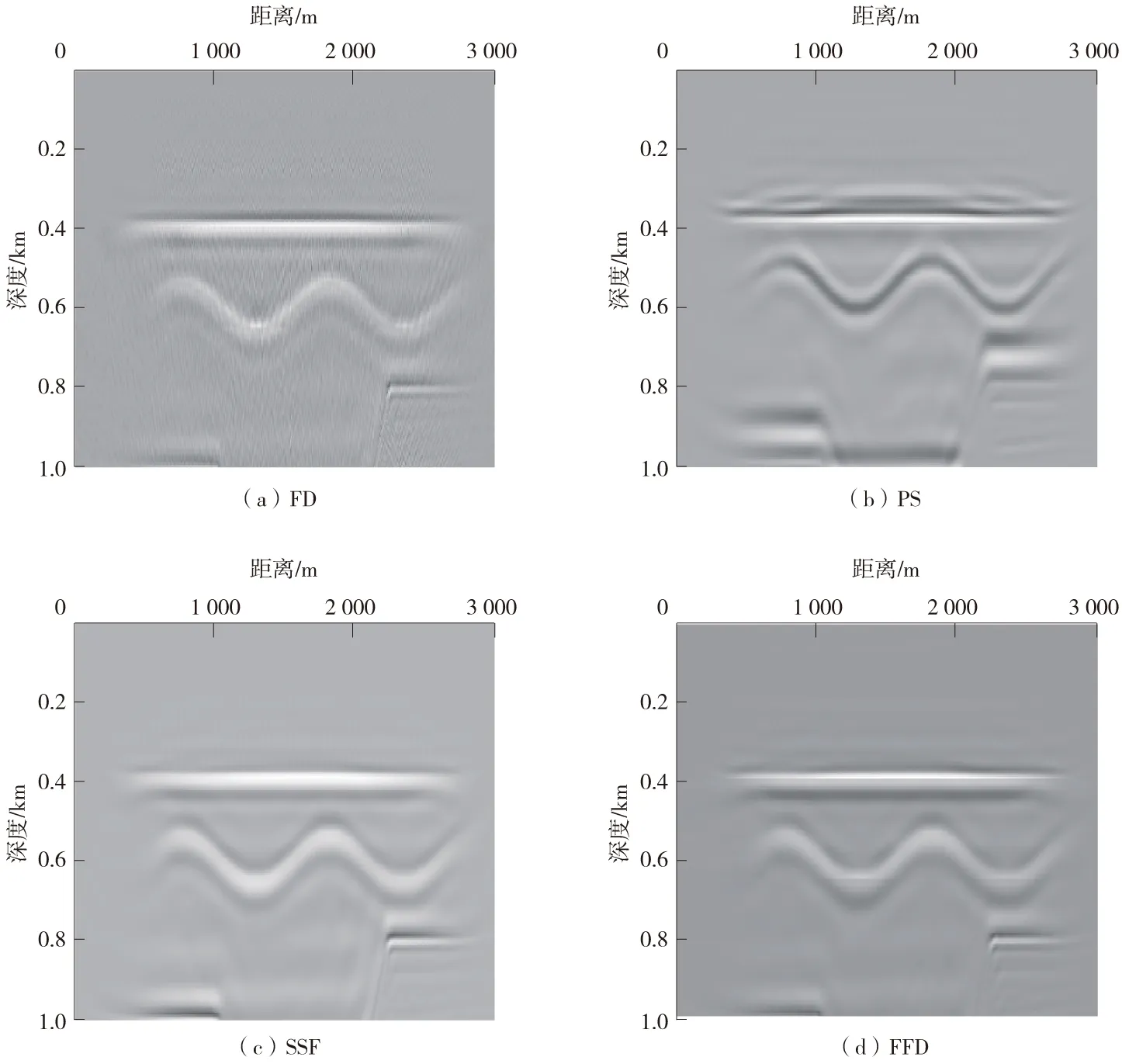
图4 不同算法的叠前深度偏移结果Fig.4 Pre-stack depth migration results of difference method
2.3 影响偏移效果的关键因素
在波动方程叠前深度偏移过程中,波场延拓步长和对边界反射的衰减函数是影响偏移效果的关键因素[19-20]。较小的延拓步长可以获得精细的成像效果,但大大增加了偏移计算的时间,为了对偏移剖面分辨率和计算时间进行兼顾,一般延拓步长取速度网格值的3~4倍为宜。
为了减小边界反射对成像剖面的影响,在波场延拓计算时需引入边界衰减函数对其进行消除或压制。典型的边界函数有e指数衰减函数、幂型衰减函数和余弦型衰减函数。3种边界函数的曲线特征如图5所示。其中,指数型函数从衰减区域到数据计算边界变化剧烈,幂型函数从模型区域到衰减区域的变化较为剧烈,而余弦型函数在衰减区域两端的变化均较为平缓。

图5 3种边界衰减函数的曲线特征Fig.5 Curve characteristics of three boundary attenuation functions
应用不同边界衰减函数对边界反射的吸收效果测试如图6所示。当对边界反射未做衰减处理时,成像剖面上有较多的同相轴假象;通过采用不同的衰减函数,剖面中的同相轴假象减弱或消失,剖面信噪比提高,表明边界反射得到不同程度的吸收衰减;对比不同边界衰减函数时的成像效果可见,余弦型衰减函数对边界反射具有最好的吸收效果。

图6 不同边界条件的处理效果Fig.6 Results from difference boundary conditions
3 结论
有限差分方法的成像效果受差分计算网格影响较大,同时差分网格会引起空间离散和假频,在偏移剖面中形成背景干扰。相移偏移具有较高的计算效率,但无法适应速度的横向变化。分步傅里叶方法在相移的基础上对速度变换引起的扰动波场进行了校正,一定程度上适应了速度的横向变化。傅里叶有限差分偏移通过时移和有限差分处理校正速度扰动对波场传播的影响,是成像效果较好的偏移方法。在波动方程叠前深度偏移过程中,波场延拓步长和边界反射衰减函数是影响其成像效果的主要因素,在成像处理中相关参数要合理选择。

