西安市PM2.5浓度的影响因素分析
贾海文,刘静静
(1.西安航空职业技术学院 航空维修工程学院,陕西 西安 710089; 2.陕汽集团商用车有限公司,陕西 西安 710089)
中国经济快速的发展和城市人口增长、工业持续发展,严重影响了大气环境的质量。针对空气质量监测,预报和控制等问题,国家和地方政府均制定了相应政策、法规和管理办法。传统的检测参数AQI 是无量纲指数,它的分项监测指标分别为SO2、NO2、CO、O3、PM2.5、PM10六项。新标准中,首次将产生雾霾的主要因素——对人类健康危害极大的细颗粒物PM2.5的浓度指标作为空气质量监测指标[1]。
随着环境污染的加重,PM2.5的研究也逐步受到更多学者的重视。吴建南等[2]采用多元线性回归和敏感性分析方法,从不同维度探索PM2.5的影响因素,表明能源消费结构、机动车尾气和建筑扬尘成为雾霾天气的直接原因;李栋等[3]运用灰色关联模型对PM2.5浓度影响因素进行分析,发现以煤炭行业为代表性的社会经济产业的关联度最大;梅波等[4]将影响PM2.5浓度的因素分为相关污染气体浓度和气象条件因素2类,分别用全模型和简化模型刻画各个影响因素的间接作用和直接作用。
综上所述,关于PM2.5的相关研究已经取得重要进展,但现有文献关于PM2.5的影响因素的研究大多仅采用一种方法,且基于大样本的统计数据探索雾霾影响因素的实证研究较少。本文从西安市日空气质量数据出发,对PM2.5浓度的原始数据进行MK(Mann-Kendall)突变检验,然后分别建立线性回归模型、分位数回归模型,对比选择出最优模型,并对PM2.5浓度的影响因素进行实证分析。
1 理论模型分析
(1)MK突变检验。MK检验用于检测序列的变化趋势以及突变点,具体方法如下:对于具有n个样本量的时间序列x,构造一致序列:
(1)

(2)线性回归模型。设解释变量y随m个解释变量x1,x2,…,xm的变化而变化,并且有线性关系:
yi=b0+b1x1i+b2x2i+…+bmxmi+εi
(2)
使用OLS法估计其中的参数b0,b1,…,bm,OLS法的思想是使残差平方和达到最小[5]。
(3)分位数回归模型。分位数回归是估计一组回归变量X与被解释变量Y之间线性关系的建模,能够更全面地反映数据信息。一般线性条件分位数回归模型:
yi(τ|xi)=b0(τ)+b1(τ)x1i+b2(τ)x2i+…+bm(τ)xmi
(3)

2 模型构建与实证分析
2.1 模型构建
(1)线性回归模型。本文利用西安市2013年12月—2019年6月的日空气质量数据建立多元线性回归方程:
Y=XB+ε
(4)

列向量Y为PM2.5浓度序列,矩阵X=(X1,X2,…,X5)分别为PM10、SO2、CO、NO2、O3的浓度;列向量B为回归系数,m=5,n=2019。为得出影响PM2.5的最佳线性回归模型[7],本文建立其他模型:
Y=X1B+ε
(2)分位数回归模型。本文利用分位数回归分析PM2.5浓度与PM10浓度、SO2浓度、CO浓度、NO2浓度、O3浓度在不同分位数下的回归系数估计量之间差异,建立以下分位数回归模型[8]:
yi(τ|xi)=b0(τ)+b1(τ)x1i+b2(τ)x2i+…+bm(τ)xmi+εi
(5)
式中,y为PM2.5的浓度;x为各解释变量;m=5;ε为误差项。
2.2 实证分析
2.2.1 数据来源
本文数据来源于西安市监测站点的2013年12月—2019年6月21日的西安市空气质量指数日历史数据(表1)[6]。

表1 西安空气质量指数日历史数据各指标Tab.1 Various indicators of daily historical data of Xi′an air quality index
2.2.2 PM2.5浓度变化及各变量间相关性分析
(1)PM2.5浓度的年度和季度变化特征。PM2.5浓度的季度变化随季节变化如图1所示。

图1 PM2.5浓度的季度变化Fig.1 Seasonal changes in PM2.5 concentration
从图1中可以看出,PM2.5浓度在2015年下降到了近几年最低值,为59.97 μg/m3,接着又连续2年上升到约71 μg/m3,在2018年平均浓度又下降到约59 μg/m3。
(2)PM2.5浓度与PM10、SO2、CO、NO2、O3浓度的分布特征(图2)。
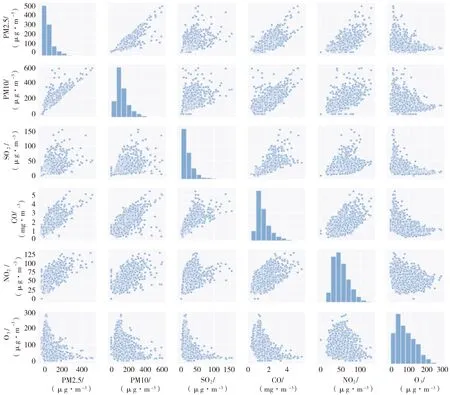
图2 PM2.5浓度与PM10、SO2、CO、NO2、O3浓度分布Fig.2 Distribution of PM2.5 concentration and PM10,SO2,CO,NO2,O3 concentration
由图2可知,PM2.5浓度与PM10、SO2、CO、NO2、O3浓度均是右偏的正态分布。上三角和下三角为它们之间的散点图。PM2.5浓度分布不是正态分布,呈右偏分布,峰度为8.68。因此,PM2.5与PM10、SO2、CO、NO2、O3,PM10与SO2、CO、NO2,SO2与CO、NO2,NO2与CO之间存在一定的相关性,而且是正相关。同时,O3与PM2.5、PM10、SO2、CO是负相关,且O3与NO2不具有相关性。
(3)不同空气质量等级与PM2.5浓度的关系(图3)。《环境空气质量指数(AQI)技术规定(试行)》规定:空气污染指数划分为0~50(优)、51~100(良)、101~150(轻度污染)、151~200(中度污染)、201~300(重度污染)和大于300(严重污染)六档,指数越大,级别越高,说明污染越严重。

图3 不同空气质量等级与PM2.5浓度的关系Fig.3 Relationship between different air quality levels and PM2.5 concentration
由图3可以看出,①空气质量等级越高,其对应的PM2.5浓度也就越高,空气质量等级与PM2.5浓度呈现出正相关关系;②异常值主要分布在严重污染和重度污染两个等级,在严重污染等级的上限和下限均存在异常值,在重度污染区域的下限存在异常值,异常值越多,则尾部越重;③异常值集中在较大值一侧,该分布呈右偏态。
(4)观测值各变量之间的相关性分析。PM2.5、PM10、AQI、CO、NO2、SO2、O3的相关系数矩阵如图4所示。
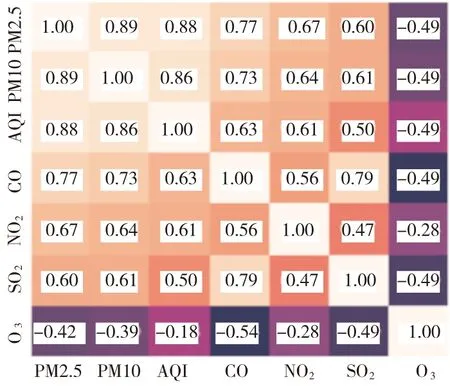
图4 相关系数矩阵Fig.4 Correlation coefficient matrix
由图4可知,PM2.5与PM10、PM2.5与AQI、PM10与AQI的相关系数都超过了0.8,为高度正相关;O3与PM2.5、PM10、CO、SO2的相关系数均为负值,说明O3与PM2.5、PM10、CO、SO2均为负相关。O3与NO2、AQI不具有相关性。
3 线性回归模型PM2.5浓度的影响因素
采用OLS回归方法对回归参数进行估计,结果见表2。

表2 4种线性回归模型的参数估计Tab.2 Parameter estimation of the four linear regression models
由表2可以看出,4个模型中第2个线性回归模型对观测数据的拟合程度较高,PM2.5浓度变化的83.11%可由PM10、CO、NO2、SO2、O3浓度的变化来解释。再从系数的显著性来看,模型一O3的显著性较低,模型二各个系数都高度显著,模型三、四中SO2浓度的系数在0.05的显著性水平下表现为不显著。即第2个模型的拟合效果最好,故选择第2个模型对PM2.5浓度的影响因素进行分析。PM2.5浓度的影响因素线性回归模型为:
(6)

该模型表明,PM10、CO、NO2浓度增加1 μg/m3时,相应的PM2.5分别增加了0.44、21.83、0.38 μg/m3;SO2浓度增加1 μg/m3时,相应的PM2.5浓度平均减少0.28 μg/m3;O3浓度每增加0.026 7%时,相应的PM2.5浓度平均减少1 μg/m3。
综上分析可知,PM10、CO、NO2浓度均对PM2.5浓度有正向关系,SO2、O3浓度对PM2.5浓度有负向影响。由该多元线性回归模型还能看出,CO的浓度对PM2.5浓度的影响效果最大,PM10的浓度对PM2.5浓度的影响效果其次,每种污染气体对PM2.5都有影响,即CO、NO2、SO2是在一定环境条件下形成PM2.5的主要气态物质。所以,降低PM10和CO浓度能够大幅度降低PM2.5浓度,提高空气质量。
4 分位数回归模型下不同分位点PM2.5浓度的变化机理
分位点及回归结果见表3。
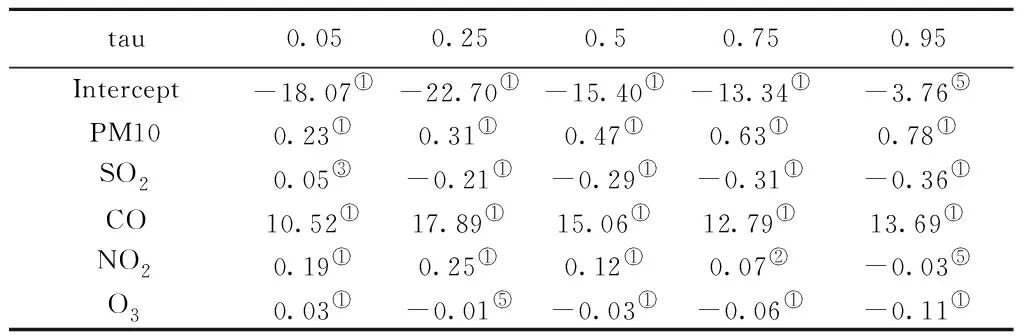
表3 分位点及回归结果Tab.3 Quantiles and regression results
由表3可以看出,对中位数回归,在选出的显著性变量下,对解释变量PM2.5贡献最大的自变量依次为PM10、CO、NO2、O3、SO2,其中CO浓度变化1单位将导致PM2.5变化15.059 9个单位。其余分位数处,CO浓度、PM10浓度、NO2浓度均显著且对PM2.5的贡献也很大。可见,CO浓度是西安市PM2.5浓度变化最主要的因素,而SO2浓度和O3浓度对西安市PM2.5浓度的影响最小。
不同分位点系数估计值如图5所示。图5中,分位数tau分别在0.05、0.25、0.5、0.75、0.95的间隔进行分布,黑色的点为不同分位数tau处的拟合回归分析,灰色的带状区域为对应回归系数的95%置信区间,不同变量的拟合回归系数的变化趋势具有一定的差异。但这些变化系数的一个共同特点是:从低分位数到高分位数的变化,置信区间带基本上都是由窄变宽,说明这些系数估计的标准差逐渐增大,估计系数的波动性逐渐增强。由图5可知,自变量SO2的拟合回归系数几乎都位于其OLS回归系数的置信区间内,说明的拟合回归系数与OLS系数之间无显著差异,而其余自变量PM10和O3的拟合回归系数与OLS系数在低分位数或者高分位数处均有显著差异,同时NO2和CO的拟合回归系数与OLS系数之间均有显著差异,说明OLS回归分析和评价各因素对PM2.5浓度的影响是不全面的,而用分位数回归会给人一种更有说服力的结果。在分位数模型拟合曲线下,各自变量的拟合回归估计大部分具有单调趋势,其中,PM10浓度呈单调递增的趋势,SO2浓度和O3浓度呈单调递减的趋势,而CO浓度和NO2浓度与PM2.5浓度均没拟合回归系数显著相关变化趋势。

图5 不同分位点系数估计值Fig.5 Estimated values of coefficients for different quantiles
5 结论
通过相关性分析发现空气污染物PM10浓度、CO浓度、SO2浓度、NO2浓度、O3浓度的变化都对PM2.5浓度的变化具有一定的影响。并将线性回归模型、分位数回归模型进行实验结果对比,通过分析,说明了因变量PM2.5浓度与其他5个自变量具有一定的相关性。分位数回归可以得出不同分位点的分布情况以及显著性水平。
(1)PM2.5浓度序列在研究期内存在下降趋势,充分证明政府的环境治理措施在近几年起到了一定的作用。
(2)PM2.5与PM10、SO2、CO、NO2,PM10与SO2、CO、NO2,SO2与CO、NO2,NO2与CO之间存在一定的相关性,而且是正相关。同时,O3与PM2.5、PM10、SO2、CO是负相关,且O3与NO2不具有相关性。
(3)空气质量等级越高,其对应的PM2.5浓度也就越高,空气质量等级与PM2.5浓度呈现出正相关关系。异常值集中在较大值一侧,该分布呈右偏态。

