面向动力学性能的薄壁加筋板结构阻尼与筋条布局协同优化设计

牛 斌 闫家铭 毛玉明 刘海洋

1.大连理工大学机械工程学院，大连,1160242.上海宇航系统工程研究所，上海,201109

0 引言

学术界针对动力学拓扑优化已展开长时间的广泛研究，包括优化结构的固有频率[1]、振型[2]、频带[3]，或者直接优化结构的动态响应，如频域下动态柔度[4]、局部位移响应[5]等。加筋结构在汽车、飞机等工业装备结构中被广泛应用，该结构的设计方法包括基结构法[6]、变厚度法[7]、均匀化方法[8]、自适应生长法[9]等，加筋结构的动力学优化研究也受到关注。为抑制加筋板的振动，INOUE等[10]对齿轮箱内的筋条进行了振动能量最小化设计研究；LI等[11]根据叶脉形成的机理对筋条进行简谐力的布局优化。此外，添加阻尼层也是提高加筋板减振能力的有效方法。在阻尼的布局优化当中，王睿等[12]以动柔度为设计目标，对受简谐外载作用附加阻尼材料的层壳体结构最优阻尼材料分布进行了研究，并通过优化算例验证了方法的合理性；ZHANG等[13]提出了一种将局部阻尼特性与单元密度联系起来的人工阻尼材料模型，研究了简谐激励下壳体结构的主结构和阻尼层的拓扑优化问题；刘海等[14]研究了加筋板自由阻尼层的优化设计；桂洪斌等[15]讨论了敷设自由阻尼层和添加黏弹性筋等两种含黏弹性阻尼的加筋结构振动特性，分析了黏弹性阻尼材料损耗因子、阻尼层和黏弹性筋尺寸的影响；臧献国等[16]以模态参与因子为设计变量对阻尼层厚度分布进行优化，结果表明，与均匀分布阻尼层相比，优化后具有不同厚度阻尼层的结构更能有效地抑制结构振动；ALFOUNEH等[17]通过移动等阈值法优化阻尼材料和基材料的分布，讨论了结构单模态阻尼比和多模态阻尼比的问题。

当前，大量文献多以单独的筋条布局优化设计或阻尼优化设计为主要研究对象，鲜见针对筋条布局和阻尼分布的协同优化设计的研究。通过筋条和阻尼布置的协同优化设计可以进一步提高结构的材料利用率，提高筋板结构的减振性能。本文提出了一种针对薄壁加筋结构的筋条布局和阻尼拓扑协同优化设计方法，通过基结构方法[18]优化筋条布局，采用各向同性材料惩罚方法(simple isotropic material with penalization, SIMP)[19]优化阻尼材料拓扑，施加筋条和阻尼材料的体积约束，实现了筋板结构最小化动态柔度设计。最后，分别在不同频率和阻尼下通过数值算例讨论了筋条和阻尼优化设计对振动响应的影响。

1 问题描述

薄壁加筋板结构阻尼拓扑与筋条布局协同优化结构模型如图1所示，在薄壁板的上下两层分别敷设加筋条和阻尼材料，薄壁板称为底板层，不参与优化。采用有限元法分析加筋结构，底板层和阻尼材料层均用板单元进行描述，加筋层离散为偏置的梁单元。在有限元分析中加筋层的偏置梁单元、底板层的板单元和阻尼材料层的偏置板单元共节点，将底板层和阻尼材料层划分为相同尺寸的网格。在有限元计算中敷设的阻尼材料层的薄壁加筋板结构总刚度矩阵K、总质量矩阵M、总阻尼矩阵C的表达式分别如下：

图1 附加阻尼材料的加筋板结构

K=Kb+Ks+Kz

(1)

M=Mb+Ms+Mz

(2)

C=Cb+Cs+Cz

(3)

式中，Kb、Ks、Kz分别为底板层、加筋层、阻尼材料层的刚度矩阵；Mb、Ms、Mz分别为底板层、加筋层、阻尼材料层的质量矩阵；Cb、Cs、Cz分别为底板层、加筋层、阻尼材料层的阻尼矩阵。

动载荷作用下阻尼材料层的薄壁加筋板结构振动控制方程为

(4)

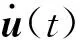
2 优化设计模型

采用基结构法对加筋层筋条布局进行优化。基结构是按一定规律布局的筋条结构，其局部3×3基结构单胞如图2所示，每个设计单胞中有6根筋条，整个加筋板由多个单胞组合构成。借助拓扑优化思想，将加筋层中筋条存在与否的离散密度情况转化为连续密度描述，为了实现如图3所示的0/1筋条布局，需在优化设计中对筋条的密度设计变量进行惩罚。在阻尼材料层布局优化中，采用变密度法，将阻尼材料层的单元密度作为设计变量，同样采用惩罚策略实现图4所示的阻尼材料层布局优化设计。

图2 加筋层基结构局部(3×3)示意图

图3 优化后筋条拓扑分布示意图

图4 优化后阻尼拓扑分布图

在协同优化过程中筋条和阻尼的设计变量都采用SIMP模型进行惩罚，带惩罚的总刚度矩阵和总质量矩阵可表示为

(5)

(6)

采用瑞利阻尼形式，加筋层、底板层和阻尼材料层的阻尼矩阵可表示为

(7)

式中，αb、αs和αz分别为底板层、加筋层和阻尼材料层的质量阻尼系数；βb、βs和βz分别为底板层、加筋层和阻尼材料层的刚度阻尼系数。

与阻尼材料层的阻尼相比，底板层和加筋层的阻尼较小，故本文只考虑阻尼材料层的阻尼效应。据此，加筋板结构的阻尼矩阵可以表示为

(8)

式中，p、q分别为阻尼的刚度和质量系数惩罚因子。

在本文数值算例中，u=3，v=1，h=3，c=3，p=3，q=3。

3 优化列式

与经典静柔度相似，结构动力学响应的度量指标定义为动柔度|PTU|(P表示载荷幅值，U表示位移幅值)，在动力学分析中外激励与振动位移的相位可能相反，因此动柔度采用绝对值的形式。本文选择动柔度平方[18]作为目标函数，同时限制加筋层和阻尼材料层的材料体积，建立如下筋条和阻尼材料拓扑协同优化列式：

(9)

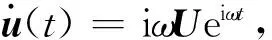
目标函数灵敏度为

(10)

其中，刚度、质量和阻尼矩阵对筋条密度和阻尼单元密度的微分K′、M′、C′分别由式(5)、式(6)、式(8)计算得到。

为了抑制拓扑优化棋盘格等数值问题，阻尼材料层采用密度过滤[19]，过滤后的单元密度

(11)

w(dl)=R-‖dl-dj‖

式中,w(dl)为权函数;‖dl-dj‖为单元l与单元j的中心点距离；Nj为第j个单元半径为R的邻域内的单元。

4 数值算例分析

图5所示为含阻尼层的加筋板，该板四端固支且在中心点受幅值为100 N的简谐激励。此算例中底板和筋条材料参数相同：弹性模量69 GPa，密度2700 kg/m3，泊松比0.33。阻尼材料层的弹性模量、密度、泊松比分别为0.22 GPa、980 kg/m3、0.49。底板的尺寸为0.5 m×0.5 m，厚度为0.002 m，筋条横截面为矩形，尺寸为0.001 m×0.003 m，阻尼层的厚度为0.002 m。底板层和阻尼层均采用50×50的四节点板单元。筋条采用铁木辛柯梁单元进行模拟，加筋层的基结构包含50×50个设计单胞。筋条体积分数最大值设定为11.25%，阻尼材料层体积分数最大值设定为40%。阻尼材料层的设计变量过滤半径为0.02 m，其大小等于两个单元。

图5 中心位置受简谐激励的四端固支方板结构

设定刚度罚因子和质量罚因子都等于1的初始设计的固有频率见表1。由频率响应图可以看出，第1阶和第6阶固有频率为共振频率。激励频率fw分别选取15 Hz(小于第一阶共振频率)、25 Hz和100 Hz(位于第一、第二阶共振频率之间)。通过施加不同频率的简谐激励，对比研究阻尼材料层和加筋层在不同的阻尼系数下的最优拓扑，相应分析结果见图6～图20。

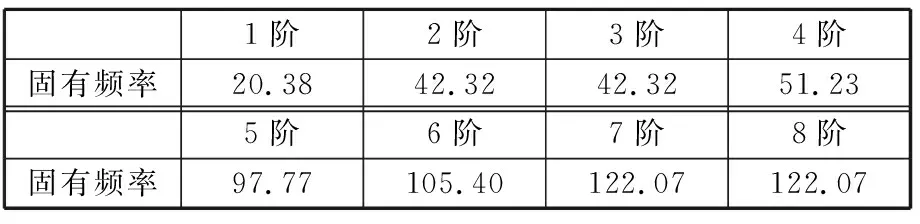
表1 含阻尼层加筋板初始设计的固有频率

考虑阻尼系数αz=0、βz=0，αz=0.05、βz=0.1和αz=0.5、βz=1三种情况，激励频率fw分别为15 Hz、25 Hz、100 Hz时优化得到的筋条分布图分别见图6、图11和图16，阻尼材料层的拓扑图分别见图7、图12和图17，优化前后结构的频率响应图分别见图8、图13和图18，优化后结构Z向(板面外方向)振动位移幅值分别见图9、图14和图19。激励频率分别为25 Hz、100 Hz，小阻尼和大阻尼情况下优化后结构Z向振动实部位移幅值图见15和图20。

(a)αz=0,βz=0 (b)αz=0.05,βz=0.1

(a)αz=0,βz=0 (b)αz=0.05,βz=0.1 (c)αz=0.5,βz=1

(a)αz=0,βz=0

(a)αz=0,βz=0 (b)αz=0.05,βz=0.1

图10 激励频率为15 Hz，阻尼系数αz=0.5、βz=1时迭代历程曲线

(a)αz=0,βz=0 (b)αz=0.05,βz=0.1

(a)αz=0,βz=0 (b)αz=0.05,βz=0.1

(a)αz=0,βz=0

(a)αz=0,βz=0 (b)αz=0.05,βz=0.1

不考虑阻尼层的阻尼效应(即αz=0,βz=0)时，采用比初始设计一阶共振频率更低的激励频率15 Hz，筋条和阻尼材料层优化结果分别如图6a、图7a所示，目标函数值从初始设计的55.38下降为0.445，优化效果显著。优化设计的筋条材料的体积分数达到上限，但阻尼材料的体积分数仅为13.2%，阻尼材料仅出现在结构的四角。若筋条布局与图6a所示相同，同时用材料将阻尼材料层填满，则该参考结构的目标函数值为0.529，基频为24.94 Hz，而图6a和图7a优化设计的基频为28.40 Hz。由此可知，只在阻尼材料层四角布置材料的优化设计会增大结构基频，减小目标函数值，而完全填满阻尼材料层反而会使基频下降，使目标函数值增大。此外，激励频率仍为15 Hz，采用αz=0.05、βz=0.1阻尼系数时的优化结果见图6b和图7b，此时使用的阻尼材料体积达到设定的最大值，阻尼材料主要集中在靠近支撑位置的板的四个角周围，对比图6b和图6a可知两种情形下筋条布局优化结果相近。采用更大的阻尼系数αz=0.5、βz=1时的优化结果如图6c和图7c所示，由图可知，结构四角处阻尼材料减少，中间位置阻尼材料增多，同时筋条布局发生了明显改变，板中部的筋条数量减少，结构边界的筋条数量增加，这表明同时优化筋条层和阻尼材料层可以降低结构动态响应。

由图8可以看出,通过优化显著降低了指定激励频率15 Hz处的结构响应，而且一阶共振峰向右移动远离该激励频率。激励频率15 Hz，阻尼系数αz=0.5、βz=1情况下的优化迭代情况见图10，其中右侧坐标轴约束体积φ为所用筋条和阻尼材料体积与所允许的筋条和阻尼材料体积的比值。由图10可以看出，随着迭代的进行，目标函数逐步下降到收敛，筋条和阻尼材料使用量逐渐增大达到允许上限。

采用比初始设计一阶共振频率更高的激励频率25 Hz，不同阻尼系数下的优化设计结果见图11和图12，可以看出不同阻尼系数下的阻尼材料层和加筋层的拓扑图有很大的不同。当阻尼较小或无阻尼时，由图11a、图11b和图12a、图12b可知，筋条以叉形分布在板的中间，阻尼在板的中间呈菱形分布；由图11c和图12c可知，考虑较大阻尼αz=0.5、βz=1 时，板的中间位置和四边分布有筋条和阻尼材料，中间位置分布的形状也不同于小阻尼时的结果。如图13所示，在没有阻尼和阻尼很小情况下，优化前后25 Hz均在一阶共振峰的右侧，阻尼很大时，一阶共振峰变平缓。考虑不同阻尼系数，计算优化后结构在25 Hz激励下的振动响应，其振动位移幅值如图14所示，对比图14b和14c可知，位移幅值图中间部分差异明显，两种阻尼下的振型虚部相似，而振型实部变化较大。图15a所示为小阻尼系数时的实部响应，对应于一阶共振峰右侧的振型，板的四边处下凹，与中心偏外的位置处相比，板的中心位置处高但低于水平面。图15b所示为大阻尼系数时的实部响应，板的中间部分是凸起的，说明实际的振型在两种阻尼下变化较大，由此可以解释25 Hz时小阻尼系数与大阻尼系数下筋条和阻尼拓扑优化设计变化较大的现象。

(a)αz=0.05,βz=0.1 (b)αz=0.5,βz=1

当激励频率达到100 Hz时，由图16a、图16b和图17a、图17b可知，在结构的四角和中间位置处分布较多的筋条和阻尼材料，在无阻尼和小阻尼的情况下，结构的振动响应振型相似(图19a、图19b)。图17a、图17b的不同之处在于，无阻尼的情况下，阻尼材料层的刚度和质量影响优化设计，而且使用的阻尼材料较少，没有达到阻尼材料用量上限，而考虑阻尼效应时阻尼材料用量达到上限，这也表明阻尼效应对降低振动目标函数的作用。但是，当阻尼系数增大至αz=0.5、βz=1时，图16c的筋条更多分布在板的中部和四边的中间位置，图17c中阻尼材料以圆形分布在板中部，与无阻尼和小阻尼情况下的筋条和阻尼材料分布明显不同，其对应的结构响应振型(图19c)相比于图19a、图19b也有较大差异。由图18可以看出，不同阻尼情况下100 Hz所处的位置是不同的，即100 Hz对应于小阻尼和无阻尼情况下的第一反共振峰的右侧(图18a、图18b)，对应于大阻尼情况下的第一反共振峰的左侧(图18c)，这也给出了优化结构在大阻尼下拓扑分布和振动响应明显差异的原因。优化后的结构在小阻尼下的振型实部图见图20a，激励的振型对应的是反共振峰右侧的振型，即板四边中间位置下凹，板中部在水平以上；优化后的结构在大阻尼下的振型实部图见图20b，激励的振型对应反共振峰左侧的振型。与图20a相比，图20b的四边中间位置下凹区域更大，板的中间位置比中部偏外位置高。

(a)αz=0,βz=0 (b)αz=0.05,βz=0.1

(a)αz=0,βz=0 (b)αz=0.05,βz=0.1

(a)αz=0,βz=0

(a)αz=0,βz=0 (b)αz=0.05,βz=0.1

(a)αz=0.05,βz=0.1 (b)αz=0.05,βz=0.1

对比图8a、图13a和图18a可以看出,优化使得相邻谐振峰值远离激励频率，从而实现降低振动响应的目标。具体如下:fw=15 Hz时一阶共振峰值右移,fw=25 Hz时一阶共振峰值左移,fw=100 Hz时二阶共振峰值右移。由图8、图13和图18可知,随着阻尼系数的增大，初始结构的响应峰值减小，而且响应峰值曲线更趋平缓。对比优化前后的振动响应，优化后的响应小于初始结构对应的响应，说明优化效果非常明显。

5 结论

本文结合基结构优化方法和阻尼材料变密度拓扑优化方法，以最小化结构动柔度为优化目标，考虑筋条和阻尼材料的用量约束，建立了筋条和阻尼材料层一体化优化模型，推导了目标函数对设计变量的灵敏度，采用梯度类算法实现筋条布局和阻尼材料拓扑的优化设计，讨论了不同的激励频率和不同的阻尼系数对优化设计的影响。本研究得出以下结论：

(1)结构优化过程中筋条与阻尼材料的分布相互影响。通过协同优化筋条和阻尼材料的分布，使相邻的共振频率远离激励频率，从而使结构在激励频率下的振动响应明显下降。当激励频率小于第一阶共振频率时，优化后第一阶共振频率向右移动，振动响应降低；当激励频率位于其他阶次共振频率之间时，优化后相邻共振频率远离激励频率，从而减小目标函数值。激励频率不同，所对应的响应模态也不同，当激励频率增大时模态复杂化，阻尼材料层和筋条的拓扑分布也随之改变。

(2)阻尼系数对阻尼拓扑和筋条布局影响较大。阻尼系数的变化不仅使结构的共振峰移动或消失，还会引起激励频率相对于初始设计共振频率的位置发生变化，影响优化后结构的振动响应模态，因此不同阻尼条件下的筋条和阻尼材料最优拓扑发生明显变化。