考虑结构柔性的电动轮毂NW行星传动啮合特性分析

谈 聪，宋朝省，朱才朝，汪建平

（1.重庆大学机械传动国家重点实验室，重庆400030；2.杭州前进齿轮箱集团股份有限公司，浙江 杭州 311203）

1 引言

纯电动汽车，由于其较低的环境、噪声污染，较高的能效和能源可回馈性，已经成为新型汽车的主要发展方向。电动汽车动力传动形式包括差减式齿轮传动、轮边齿轮传动与轮毂齿轮传动，其中，轮毂齿轮传动直接将电机和动力减速部分集成在轮毂中，使得驱动系统结构更为简洁，省略了传统的离合器，从而有效地利用了空间，简化了整车结构，提高了传动效率。然而一体化紧凑设计也带来一系列技术问题，如电机输入转速高，轮毂输出扭矩大，行星减速机构的齿轮磨损较快，润滑、散热困难等问题。其中电动车轮毂行星减速机构起到了减速增扭的作用，是整车中故障多发部位，直接影响整车动力性能与乘车舒适性。因此，对电动汽车轮毂行星齿轮传动进行啮合特性研究，提高轮毂齿轮传动的啮合性能与减振降噪具有重要意义[1]。

国内外学者对行星齿轮传动的啮合特性进行了一定的研究。文献[2]通过实验研究了2K-H型行星传动齿圈厚度对齿圈齿根应力的影响，还研究了齿圈齿数对齿根应力的影响。文献[3]通过实验和理论的方法研究了齿圈厚度对齿圈变形、应力、行星轮均载的影响，指出在齿圈设计时齿圈的变形和支撑条件必须给予考虑。文献[4]通过有限元方法研究了薄内齿圈的齿圈厚度对齿根应力和齿圈变形的影响。文献[5]创建了整个行星齿轮组的非线性变形体模型，以研究轮缘柔性（尤其是内齿轮）对静态条件下的齿轮应力和行星均载的影响。文献[6]以2K-H型行星齿轮传动为对象，采用有限元方法建立了柔性齿圈模型，求解了系统固有频率与振型，阐述了耦合系统固有频率的分布规律，讨论了齿圈厚度对系统固有频率分布、子系统耦合阶次与振动模式的影响。文献[7]以NGW型直齿行星传动为例计入齿圈柔性的行星传动建立了动力学模型，得出齿圈柔性对系统固有频率的影响。文献[8]采用ABAQUS有限元软件分析了两种齿圈形状的应力和变形的情况，同时分析了齿圈厚度对齿轮副啮合刚度的影响。文献[9]研究了风电齿轮箱中柔性销轴的位置误差对行星轮均载问题。文献[10]通过实验和软件分别分析了NGW型行星齿轮的均载并做了对比分析。

综上所述，当前研究主要针对单级的行星齿轮传动展开，而对NW型行星齿轮传动的研究较少。本文以电动轮毂NW行星传动为研究对象，在考虑内齿圈柔性条件下，建立了NW行星传动的啮合分析模型，研究了柔性齿圈的厚度对于齿圈变形以及系统传动误差的影响、轮齿的接触应力及修形分析、销轴位置误差对行星传动均载的影响。研究结果对电动轮毂NW行星传动的优化设计具有重要的意义。

2 电动轮毂驱动结构与传动原理

电动车轮毂驱动的结构，如图1所示。左侧为电机部分，右侧为一NW型行星齿轮减速部分。由电机的转子作为动力驱动部件，带动太阳轮作为右侧行星齿轮的输入，由连接到轮毂的行星架作为动力输出，NW行星传动原理，如图2所示。在设计轮毂齿轮传动时，由于减速部分存在双联行星齿轮，所以为了保证正确的啮合，行星齿轮的参数应该要满足：传动比条件、同心条件、装配条件和邻接条件。综合考虑，设计轮毂NW行星传动的参数，如表1所示。行星齿轮参数约束条件，如表2所示。

表1 NW行星齿轮传动几何参数Tab.1 Geometric Parameters of NW Planetary Gear Transmission

表2 NW行星齿轮传动齿数确定条件Tab.2 Constraint Conditions of NW Planetary Gear Transmission

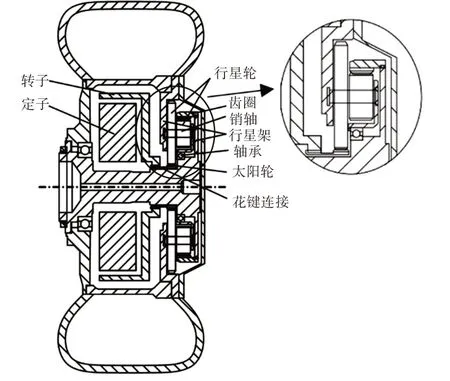
图1 电动轮毂结构示意图Fig.1 Schematic Diagram of Electric Wheel Hub Structure

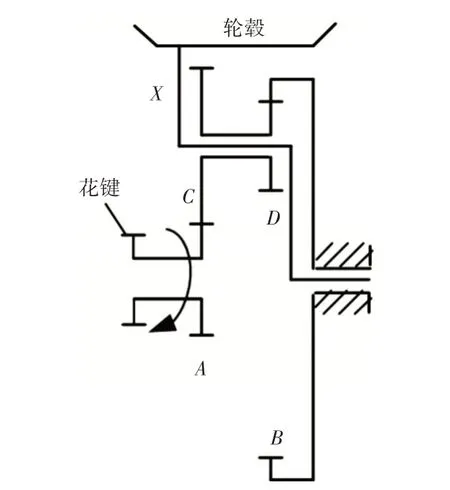
图2 NW行星齿轮传动原理图Fig.2 Transmission Principle Diagram of NW Planetary Gear

图中：A—太阳轮；B—齿圈；C、D—双联行星齿轮；X—行星架。

表中：z A，z B，z C，z D—齿轮的齿数；r ac—双联行星齿轮中较大的齿轮的齿顶圆半径；L—相邻两个行星齿轮的中心距；a AC，a BD—两级齿轮副的中心距；s—双联行星齿轮z C，z D的公因子；n p—行星轮个数，如图3所示。

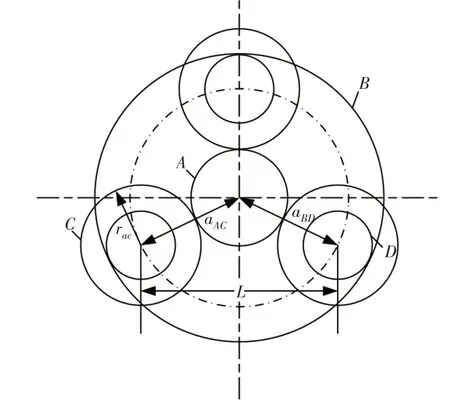
图3 约束条件中的参数表示Fig.3 Parameter Description of the Constraints

为了考虑齿圈的柔性作用，采用耦合节点与齿圈连接，如图4所示。以ANSYS建立齿圈模型，并建立耦合节点，从ANSYS中提取齿圈刚度矩阵和节点位置信息，在专业设计软件MASTA中建立行星传动机构仿真分析模型，利用所建立的节点进行齿圈的耦合，对行星传动机构进行柔性分析。获取齿圈刚度矩阵和节点位置的分析流程，如图5所示。NW行星齿轮分析模型。模型所取太阳轮的输入转速为6000r∕min，输入的功率为380kW，如图6所示。

图4 齿圈的耦合节点Fig.4 Coupling Nodes of the Ring Gear

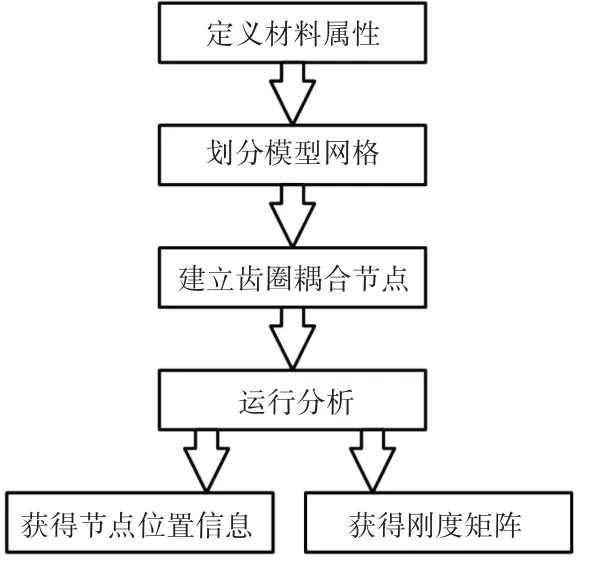
图5 提取齿圈刚度矩阵和节点位置分析流程Fig.5 Analysis Process of Extracting Ring Gear Stiffness Matrix and Nodes Position

图6 NW行星传动系统分析模型Fig.6 Analysis Model of NW Planetary Transmission System

3 考虑柔性齿圈的啮合特性分析

3.1 齿圈变形分析

在轮毂轻量化的发展趋势下，设计内齿圈时往往希望尽可能减薄其轮缘厚度，以减小整机尺寸、减轻装置质量。但轮缘过薄对齿圈变形将产生不利影响从而降低承载能力。为了分析柔性内齿圈的厚度的影响，分别选取齿圈的直径为394mm，398mm，402mm，研究齿圈厚度对齿圈变形的影响。

对轮缘厚度系数，如图7所示。Γ的定义[3]为：

图7 轮缘厚度系数定义图示Fig.7 Diagram of the Definition of Rim Thickness Coefficient

式中：t=R OD-Rroot，Rmean=(R OD+Rroot)∕2；R OD—内齿圈外圆半径；Rroot—内齿圈齿根圆半径；Rmean—平均半径。根据不同齿圈厚度，得到Γ的值分别为0.039，0.049，0.059。

在不同的齿圈厚度下，柔性齿圈的变形情况，如图8所示。

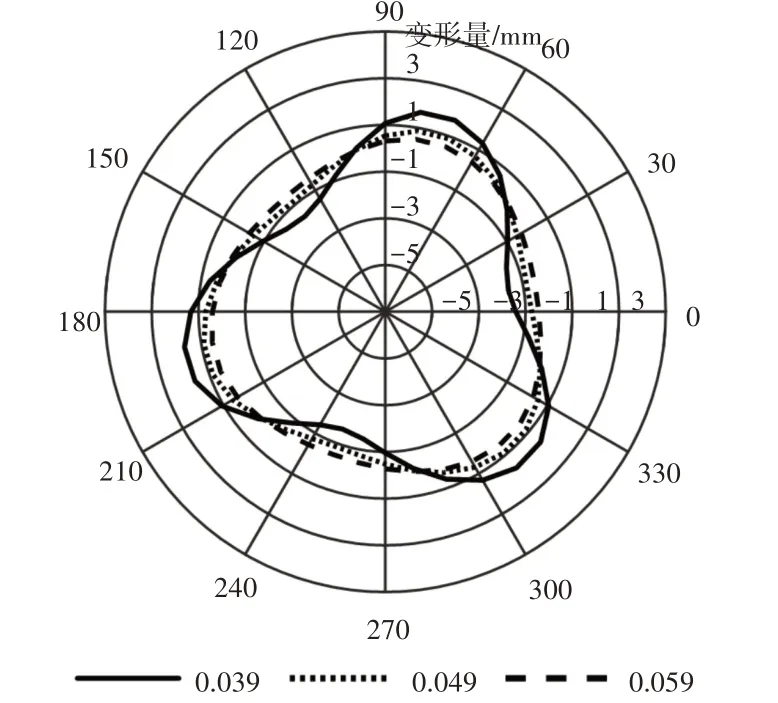
图8 柔性内齿圈的变形图Fig.8 Diagram of Deformation of Flexible Ring Gear

从计算结果可以看出，在同一工况条件下，齿圈厚度与齿圈的变形量有很大的关系，随着齿圈厚度增大，齿圈的变形量大大减小。当Γ为0.039时，最大变形量为1.73mm；当Γ为0.049时，最大变形量为0.89mm；当Γ为0.059时，最大变形量为0.52mm。相比之下，随着齿圈厚度的增大，齿圈的最大变形量有较大的减小，但并不是呈线性的变化。

3.2 齿轮系统传动误差分析

齿轮系统的传动误差表示为太阳轮输入到行星架输出之间的传动误差，其计算公式为：

式中：Δθ—系统的传动误差；θinput—太阳轮的输入角度；θoutput—行星架的输出角度；i—齿轮系统的传动比。

不同齿圈厚度对NW行星传动系统传动误差的影响，如图9所示。

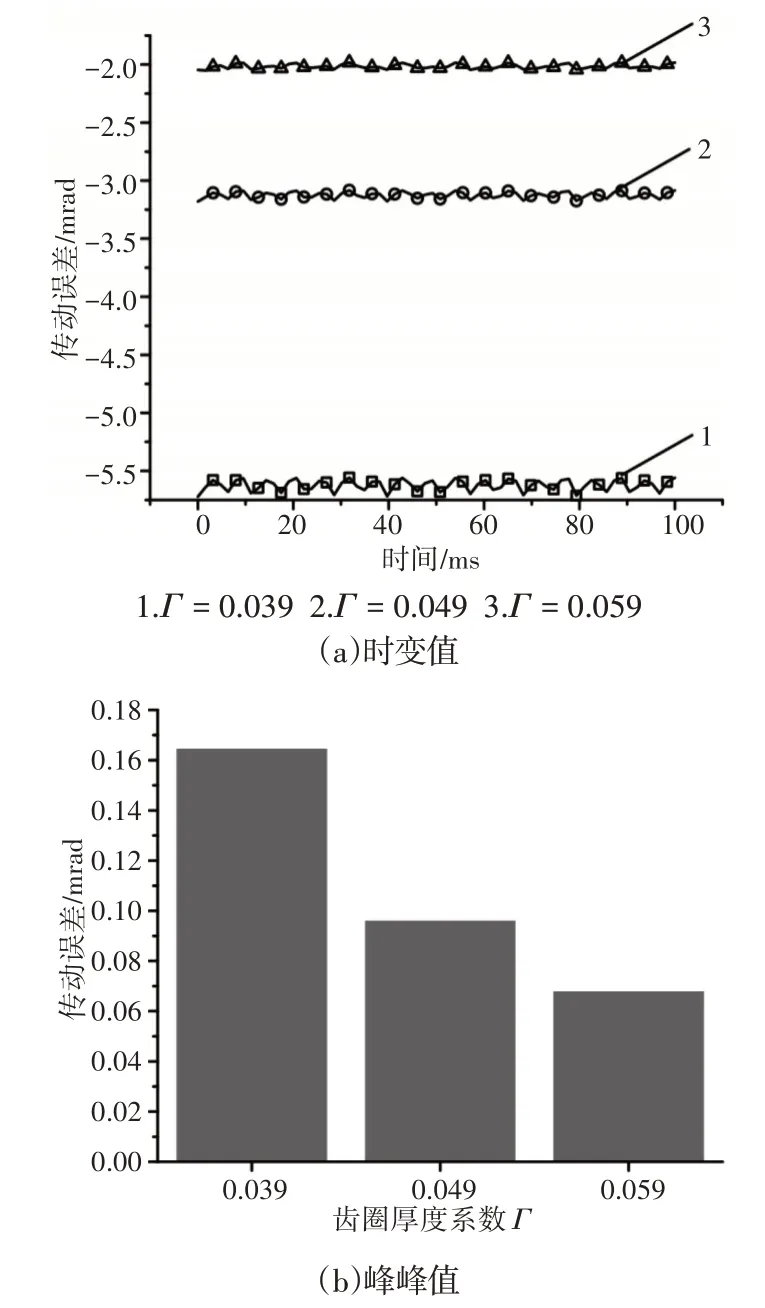
图9 行星齿轮传动误差Fig.9 Transmission Error of Planetary Gear

可以看出，随着齿圈厚度系数的增大，行星齿轮系统的传动误差会有所减小，这是由于齿圈越厚，系统的刚性越好，因此传动误差会随齿圈变厚而减小。与此同时，从图9（b）看到传动误差的峰峰值也会减小。

3.3 轮齿接触应力与修形分析

电动车轮边减速器在高速转动工况下，齿轮传动系统同时受到内外激励载荷共同作用，其受力振动状态复杂。轮齿修形则可有效弥补由齿轮啮合引起的弹性变形、热变形、安装误差、实际啮合引起的基节偏差等，消除或减轻齿向与齿形方向载荷集中问题，减小齿轮传动中的啮合冲击振动和噪声等[11]。

利用有限元方法计算齿轮啮合时的接触应力之前，需对齿轮进行网格划分。由于齿轮接触区域很小，需要对接触齿面的有限元网格加密。采用六面体实体单元划分网格，得到太阳轮单元数目为37824，双联行星轮单元数目分别为57936和14972，齿圈单元数目为79236，如图10所示。边界条件为约束齿轮的径向和轴向位移，只保留沿轴向的转动自由度。在主动轮上施加轴向的角速度载荷，在从动轮上施加扭矩，然后求解。

图10 齿轮的有限元模型Fig.10 Finite Element Model of Gear

未修形条件下行星齿轮系第一级和第二级接触印痕，可以看出第一级行星齿轮存在两端偏载，第二级行星齿轮存在左端偏载，如图11所示。

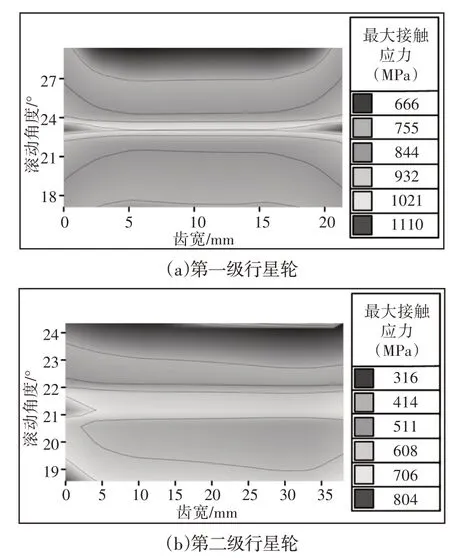
图11 行星轮接触应力Fig.11 Contact Pattern of Planetary Gear

齿向修形可以改变啮合印痕沿齿宽方向的分布，齿廓修形可以改变啮合印痕沿齿形方向的分布。为了改善每一级齿轮副的啮合情况，对太阳轮轮齿的齿向方向做鼓形修形，对齿廓方向做鼓形修形和边坡修形；对内齿圈轮齿的齿向和齿廓方向同时做起鼓修形和边坡修形。太阳轮与齿圈的修形量，如图12所示。

通过分析，修形后的轮齿接触印痕，如图13所示。可以看出，最大载荷区域向齿面中心移动，边缘载荷现象消失，齿面载荷分布更加均匀，各齿轮副在齿宽方向和齿廓方向的偏载现象得到很大的改善。

图13 修形后行星轮接触应力Fig.13 Contact Pattern of Planetary Gear with Modifications

4 NW行星传动均载分析

4.1 单个销轴位置误差对行星齿轮传动的影响

行星齿轮传动通过多分支功率分流传递功率，会造成各分支传递的载荷不均，其不均匀程度可以用均载系数Kγ来表示。Kγ定义为行星轮分支的转矩与每分支的平均转矩之比，其计算公式为：

式中：Tbranch—行星轮分支的转矩；T nom—总额定转矩；n p—行星轮个数。

行星轮销轴安装到行星架上，行星轮安装到行星轮销轴上，因此行星轮销轴的位置误差对行星轮之间的均载有着重要的影响。行星轮销轴的位置误差可以有三种不同的表示方式，如图14所示。行星轮销轴位置的径向误差表示为e ra d，切向误差为etan。当销轴靠近太阳轮时e r a d为负值，远离太阳轮时e rad为正值；当销轴为顺时针方向的切向位置误差时etan为正值，逆时针方向时etan为负值。

图14 行星齿轮销轴的位置误差示意图Fig.14 Diagram of Pin Position Error of Planetary Gear

当行星齿轮销轴的位置误差不同时，行星齿轮的均载也会不同。在齿圈厚度系数Γ为0.059的情况下，仅考虑行星轮p1的切向位置误差时，每个行星齿轮的均载变化情况，如图15所示。仅考虑行星轮p1的径向位置误差时，每个行星齿轮的均载变化情况，如图16所示。可以看到，随着误差的增大，行星齿轮的均载系数增大。销轴的切向位置误差对行星齿轮的均载影响是较大的，尤其是对本身产生位置误差的销轴所在行星轮影响更大，当etan=-300μm时，p1行星轮的均载系数为1.1569。而销轴的径向位置误差对行星齿轮的均载影响较小。同时，当行星销轴的径向位置误差为正值（行星销轴远离太阳轮）时，对行星轮的均载影响较小。

图15 均载系数与p1销轴切向位置误差etan的关系Fig.15 Relationship Between Load Sharing and the Tangential Position Error etan of p1 Pin

图16 均载系数与p1销轴径向位置误差e rad的关系Fig.16 Relationship Between Load Sharing and the Radial Position Error e r ad of p1 Pin

销轴切向和径向位置误差同时存在时的行星齿轮均载情况如图17所示。可以看出，销轴切向和径向位置误差同时存在时对行星齿轮的均载系数影响较大，当etan=e ra d=-300μm时，行星轮p1的均载系数为1.1391，行星轮p3的均载系数为0.8818。

图17 p1销轴切向、径向位置误差下行星齿轮均载Fig.17 Load Sharing of Planetary Gear under the Tangential and Radial Position Error at p1 Pin

4.2 多个销轴位置误差对行星齿轮传动的影响

考虑两个销轴切向位置误差且每个销轴切向位置误差一致时，行星齿轮的均载情况，如图18所示。当两个行星齿轮存在相同的切向位置误差时，对行星齿轮的均载情况影响很大，由于行星齿轮的对称性，其影响结果与只考虑单个销轴切向位置误差时的情况相似。

图18 p1、p2行星轮切向位置误差相等时的均载系数Fig.18 Load Sharing with Equal Tangential Position Error at p1 and p2 Pins

当考虑三个行星轮都存在相同的切向位置误差时的均载情况。可以看到其对均载的影响很小，如图19所示。

图19 p1、p2、p3行星轮切向位置误差相等时的均载系数Fig.19 Load Sharing with Equal Tangential Position Error at p1、p2 and p3 Pins

通过对比分析可知，单个行星齿轮存在位置误差对行星齿轮会有明显的载荷不均匀现象；而当每个行星齿轮有相同的位置误差时，对均载情况影响较小，说明他们之间会相互抵消部分误差而对均载得到改善。

5 结论

论文考虑齿圈柔性，建立了电动轮毂NW行星传动的三维啮合模型并进行了啮合特性与均载分析，得出了如下结论：

（1）通过建立齿圈耦合节点，计算齿圈的变形，得到柔性齿圈的变形量与齿圈的厚度有关，随着齿圈厚度的增大，齿圈的最大变形量会有较大的减小，但并不是呈线性的变化。随着齿圈厚度增大，传动误差峰峰值减小；

（2）在给定工况下，分析轮齿的啮合印痕，提出修形方案，有效地改善了原有电动轮毂NW行星齿轮传动轮齿啮合偏载现象；

（3）在电动轮毂NW行星传动中，销轴的切向位置误差对行星轮均载影响较大，而径向位置误差对均载影响较小，在设计行星齿轮时要给予重视。