涂料干燥过程中溶剂扩散系数的预测与测试方法
毕月姣,郑振荣, ,仝丽欢,刘娅岚
(1.天津工业大学纺织科学与工程学院,天津 300387; 2.天津工业大学先进纺织复合材料重点实验室,天津 300387)
涂层是将聚合物溶液或其他材料涂覆在基材上,赋予基材特定性能的技术,不仅可以提升材料的使用价值,还可延长其使用寿命,被广泛应用于建筑、医疗、装饰、交通及军事领域[1-3]。干燥是涂料固化过程中关键的工艺步骤,不仅决定了薄膜中残留溶剂的含量,还影响其性能[4-5]。目前研究涂层干燥固化过程的方法主要有试验法和数值模拟法,但试验法一般需进行重复实验,成本高、周期长,且部分溶剂会破坏环境。而数值模拟能在很大程度上提高研发效率,更利于节能环保。因此,干燥过程模型化已成为涂膜干燥过程的主要研究方向之一。
溶剂扩散系数是控制干燥速率的关键因素,是烘干过程非常重要的动态物理参数,它能准确反映溶剂小分子在溶液中的扩散行为。溶剂扩散系数的预测模型主要有阻塞效应模型、自由体积模型和流体力学模型。其中以自由体积模型应用最为广泛[6-7],该模型的主要特征是自由体积的可加性和自由体积中每个增量单元组分特性的可靠性。这些特征允许模型可以利用从单个组分(如纯聚合物或纯溶剂)实验数据中提取自由体积参数或其他参数来分析聚合物-溶剂系统。准确获得溶剂的扩散系数,不仅可为后续建立涂层的固化模型提供理论基础,还可为涂层的性能研究和干燥条件的优化提供理论指导。
本文基于自由体积理论,详细介绍了溶剂扩散系数的计算公式,以及公式中各参数的计算方法,并进一步以聚甲基丙烯酸甲酯-丙酮涂料为例,利用自由体积模型实现了溶剂扩散系数的预测,并探究了溶剂扩散系数与温度和溶剂浓度的关系,最后通过称重法和热重分析法对溶剂扩散的预测值进行了验证。
1 涂料溶剂扩散系数的预测模型
自由体积理论是Cohen和Turnbull[8]在模拟简单液体扩散时首次提出的,他们认为液体分子由于热运动会在自身周围产生自由体积,当自由体积大到可以被紧邻的液体分子填充时,扩散就发生了。简单液体扩散系数D的表达式如式(1)所示。

其中K为比例常数(无量纲),γ为重叠因子,V*为分子临界空穴自由体积(单位:cm3/g),Vf为体系中总的自由体积(单位:cm3/g)。
Fujita[9]首次用自由体积理论解释了溶剂在高聚物体系中的扩散行为,并提出了溶剂分子扩散系数的表达式(式2),其不足之处是只可用来研究溶剂浓度非常低的体系。

其中D0是指前因子(单位:cm2/s),是聚合物体系中每个分子的平均空穴自由体积(单位:cm3/g),是溶剂分子跃迁到新位置时所需的临界空穴自由比容(单位:cm3/g),Ea是扩散活化能(单位:J/mol),R是理想气体常数[8.314 J/(mol·K)],T表示热力学温度(单位:K)。
随后人们引入分子碰撞、跳跃单元、相互作用力以及高聚物大分子之间的纠缠等概念,对自由体积理论进行了改进和完善。Bhargava等[10]认为在溶剂-聚合物二元涂层体系中,溶剂由于自身浓度梯度以及分子间的相互作用而发生扩散,因此在一个点处溶剂浓度的变化率等于在那一点的流量梯度,于是获得了更完善的扩散系数计算方法,见式(3)。
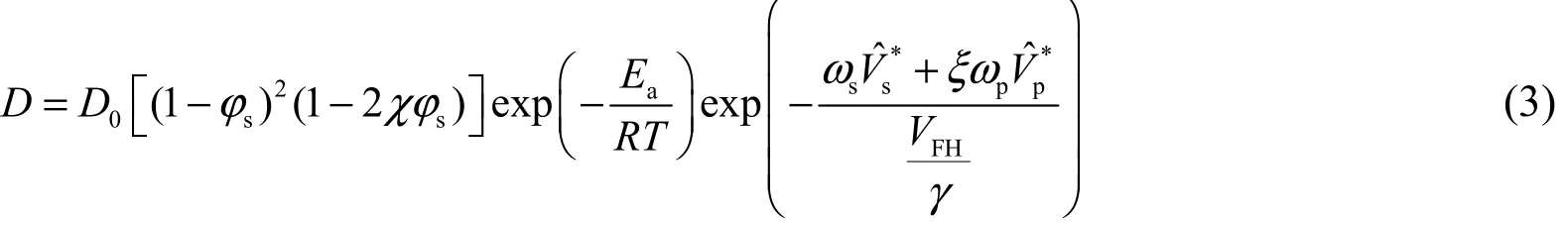
其中φs是溶剂体积分数,χ是溶剂-聚合物系统的相互作用参数(无量纲),ws和wp分别是溶剂和聚合物的质量分数,和分别代表溶剂和聚合物产生迁移时所需的临界空穴自由比容(单位:cm3/g),ξ是溶剂和聚合物迁移单位摩尔体积的比值,FHVγ是溶剂和聚合物的自由体积(单位:cm3/g)。γ取值范围为0.5 ~ 1.0,表明不同的迁移单位可跳跃到同一个空穴空间。
1.1 预测模型中各参数的计算方法

表1 常见溶剂和高聚物的临界自由比容[12] Table 1 Critical free specific volume of common solvents and polymers [12]
VFHγ的计算如式(4)所示。

其中K11γ与K21-Tgs是溶剂的自由体积参数,K12γ与K22-Tgp是高聚物的自由体积参数。溶剂的自由体积参数可通过Doolittle等[13]提出的黏度-温度经验公式[即式(5)],采用非线性回归的方法得到。

其中M1是溶剂分子的摩尔质量(单位:g/mol),为溶剂分子的临界摩尔体积(单位:cm3/mol),η为溶剂的黏度(单位:Pa·s),V1溶剂在温度T时的比容(单位:cm3/g),是溶剂的临界空穴自由体积(单位:cm3/g)。另外,聚合物的自由体积参数K12和K22与WLF常数相关联,WLF可在相关文献及手册中查到[14]。
χ是溶剂-聚合物体系的相互作用参数,由Bristow和Waston开发的半经验方程确定[6],见式(6)。

其中δs和δp分别是溶剂和聚合物的溶解度参数,Vs为溶剂的摩尔体积,可查阅文献[15]。
Ea可以根据Reis等[16]提出的式(7)进行求解。

Ju等[17]指出ξ在0 K时与溶剂摩尔体积()之间的线性关系如式(8)所示。


1.2 计算实例
将聚甲基丙烯酸甲酯(PMMA)溶于有机溶剂,如丙酮、苯酚等,可获得良好的薄膜。该薄膜透明、不易泛黄,具有良好的介电性、化学稳定性、耐候性和阻燃性,被广泛用作晶体管的介质层、船体的防腐层、光学薄膜、户外建材、街头标牌装饰等。本文选择了应用较广的PMMA-丙酮二相体系作为计算实例,根据上述各参数的计算方法,该体系的自由体积参数列于表2。

表2 PMMA-丙酮体系的自由体积参数 Table 2 Free volume parameters of PMMA-acetone system
针对PMMA-丙酮体系,利用改进的自由体积模型预测了溶剂在涂层液中的扩散系数,研究了温度(0、25和30 °C)及溶剂质量分数(0% ~ 90%)对溶剂扩散系数的影响,预测模型的部分程序代码列于表3。另外,只需要改变程序中温度和溶剂浓度的数值以及涂料体系的自由体积参数,即可用于预测其他涂料体系中溶剂的扩散系数。

表3 改进的自由体积模型程序代码 Table 3 Program code for the improved free volume model
1.3 测试方法
测试溶剂扩散系数的方法主要有反气相色谱法、脉冲梯度核磁共振法、激光全息技术法、热重分析法、称重法等[19-22]。前3种方法主要测定无限稀释条件下高分子溶液中的扩散系数,精准性较高,但操作复杂,成本较高。热重分析法和称重法均是根据质量与时间的关系绘出函数曲线,由曲线方程计算出溶剂的扩散系数,虽然精准性稍差,但是操作简单,便于观察溶剂-聚合物涂层体系溶液的烘干过程,应用较广泛。
热重分析仪可以连续记录质量和温度的相互变化关系。涂料在测试中会受热发生升华、汽化、分解等变化,就会发生质量损失,根据质量与温度及时间的关系,可以绘制出温度或时间与质量损失的关系 曲线,加以分析后便能获得想要的数据。按式(10)以对作图,根据斜率和截距求出D0和Ea。代入式(11)可计算出不同温度和浓度下的扩散系数[19]。

其中Mt和M∞分别为涂料的初始和最终质量(单位:kg),r0为PMMA粒子半径(单位:m,可由激光粒度仪测得),β为升温速率(单位:°C/min)。
称重法是在恒温的条件下利用分析天平和秒表记录涂层液质量随时间变化的数据。在涂层液中,假设PMMA粒子为均匀的球体,且研究的时间相对较短,张晓彤等[22]由菲克第二定律推导出了小分子的瞬时扩散方程如式(12)所示。

其中 0Q、tQ和Q∞分别为初始涂层质量、瞬时涂层质量和最终涂层质量(单位:kg),t为扩散时间(单位:s)。
2 结果与讨论
2.1 溶剂扩散系数的预测结果
基于自由体积模型,将表2中的数据代入式(3)至式(8)中,计算得到扩散系数与溶剂质量分数ws和温度T的关系,结果如图1所示。溶剂的扩散系数随着溶剂质量分数增加呈现出先升后降的趋势。当溶剂质量分数为0% ~ 40%时,溶剂浓度非常小,而聚合物浓度很大,分子间作用力由聚合物决定,溶剂扩散系数随着聚合物含量的降低而增大。当溶剂质量分数大于40%时,体系中溶剂分子较多,溶剂分子的自由体积将占据主导地位,溶剂含量越高,分子间作用力越大,扩散系数随溶剂浓度的增加而降低。此外,当溶剂质量分数一定时,溶剂扩散系数随温度的升高而增大。这是因为温度升高加剧了溶剂分子的运动和碰撞,使分子偏离初始位置的距离增大,相互作用力减弱,利于扩散。

图1 温度和溶剂质量分数对扩散系数的影响 Figure 1 Effects of temperature and solvent concentration on diffusion coefficient
2.2 热重分析法测试溶剂扩散系数的结果
根据热重数据(tM、M∞与T的关系)和式(10),通过作图可求出溶剂的指前因子D0和扩散活化能Ea,继而由式(11)求出不同温度下丙酮的扩散系数D。利用热重分析仪测试涂料的扩散系数时,设置温度范围为20 ~ 300 °C,升温速率为2 °C/min,取26.4 mg涂料放入空坩埚中,选择空气环境对试样进行测试。以溶剂质量分数80%的涂层液为例,求取温度为25 °C的涂层液中溶剂的扩散系数。
由图2可知,涂料在52.4 °C时质量损失速率最大,此时已升温了16 min,质量损失率达到了57.01%。在52.4 ~ 200.0 °C的温度范围之内,涂料的质量变化缓慢,仅下降了6.94%,此时测试经历了90 min,涂液的挥发已基本完成,体系的残留质量为36.05%。根据涂料的质量损失率、残留质量、温度和时间的 关系,设,作如图3所示的图,得到的校准方程为lnC= -24.027 43 + 0.853 44/T, 校准因子R2= 0.999 48。根据式(10),得到lnD0= -24.027 43和-= 0.8673,再由式(11)计算出25 °C 下溶剂的扩散系数D= 3.660 0 × 10-11m2/s。与预测模型得到的D= 1.003 6 × 10-11m2/s相差较大。分析其原因是样品较少,从向坩埚中添加样品,称重,再将样品固定到仪器的样品台,随后打开已设置好的试验参数进行测试,一系列操作尽管娴熟但仍需一定时间,再加上丙酮是常温下挥发性极强的溶剂,导致涂液的总质量降低,所以实验误差偏大。可见热重分析法不适合测试挥发性较强的溶剂的扩散系数。

图2 热重分析曲线 Figure 2 Thermogravimetric analysis curve

图3 lnC和1/T的关系曲线 Figure 3 Curve showing the relationship betweenlnCand 1/T
2.3 称重法测试溶剂扩散系数的结果
在25 °C的条件下,通过称重法测试了溶剂质量分数分别为60%、70%、75%、80%、85%和90%的涂料的扩散系数,具体操作如下:(1)设置恒温培养箱的温度为25 °C;(2)将分析天平放入培养箱中,调节至平衡,使显示屏示数为0;(3)分别取5 mL溶剂质量分数不同的涂料倒入培养皿中,然后置于天平中,观察并记录培养皿中溶液质量随时间的变化。为了减少操作误差,进行了多次重复试验。以质量分 数85%为例,根据一次试验记录的数据,以对作图。由式(12)可知,该曲线的斜率即为 溶剂的扩散系数。
由图4可知,随着时间推移,曲线斜率先增大后减小,瞬时扩散系数随之先增加后减小。这是因为:扩散初期丙酮分子较多,分子间作用力较强,分子的自由度很小,扩散阻力很大;随着时间延长,溶剂不断挥发,溶剂分子间的作用力减小,扩散阻力减小,扩散系数增加;在扩散后期,体系中的溶剂分子很少,聚合物大分子排列紧密,体系中的自由体积很少,扩散阻力大,于是扩散系数降低。

图4 与的函数关系 Figure 4 Functional graph of and
由于某浓度下的扩散系数为该浓度下一秒内通过单位面积的扩散通量,且溶剂扩散较快对于实验的第一秒难以控制,会导致计算结果误差偏大,因此利用10 s后精准记录的时间与涂层液质量的数据,以对时间t作图,见图5。其拟合方程如下:
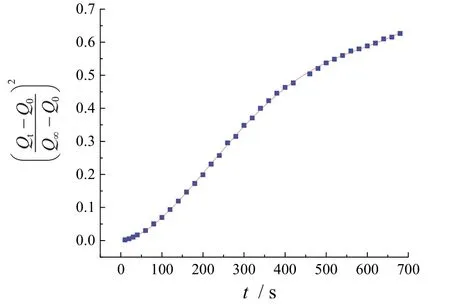
图5 与时间的关系曲线 Figure 5 Curve showing the relation between and time

当t= 1时,。再由式(12)得到扩散系数D= 5.527 9 × 10-12m2/s。
重复上述计算方法,计算出溶剂质量分数分别为60%、70%、75%、80%和90%时涂料的扩散系数,并与25 °C下溶剂扩散系数的预测值进行对比,结果见图6。

图6 称重法获得的扩散系数与预测值的对比 Figure 6 Comparison between diffusion coefficients obtained by gravimetric method and predicted values
总的来说,模拟值与实验值的吻合程度较高,说明可以利用改进的自由体积模型预测涂料体系的扩散系数。溶剂质量分数为60%、70%和75%时,实验值与模拟值的误差相对大一些,而溶剂质量分数为80%、85%和90%时误差较小,说明溶剂质量分数越高,模拟值与实验值越接近。另外,预测曲线基本位于实验值的下方,说明模型预测的扩散系数比实际测得的扩散系数稍小,这是因为利用模型计算时把溶剂-聚合物体系的自由体积参数当成定值,忽略了浓度对自由体积参数的影响。
3 结论
采用改进的自由体积模型对聚甲基丙烯酸甲酯-丙酮体系中溶剂的扩散系数进行计算,并与热重分析法和称重法的测量结果进行对比,得到如下结论:
(1) 当溶剂质量分数一定时,扩散系数随温度的升高而增大。
(2) 当温度一定时,溶剂扩散系数随质量分数的增加呈现出先增后减的趋势,在质量分数40%左右出现峰值。
(3) 模型预测的扩散系数与重量法的测试值吻合程度较高,说明预测模型能较准确地反映涂料在干燥过程中的扩散行为。这不仅能够令人们增强对涂层成膜过程的认识,还有益于节能环保地进行涂层产品的设计及涂层工艺的优化。
(4) 热重分析法不适用于挥发性较强的溶液扩散系数的测定。

