金融数学的随机变量假设错误及纠正
高宏 梅圣烽

本文从随机变量和随机过程的定义出发,分析了金融数学在建立股票价格模型时,将股票价格与时间之间的数量关系抽象为随机变量的基本概念错误,无形中导致研究对象从一个样本函数改变为样本函数的集合,从而推导出了“股票价格服从对数正态分布”这一与事实不符的错误结论。本文将股票价格与时间之间的数量关系还原为时间函数,根据“股票价格的对数收益率为白噪声序列”的实证研究结果,建立了可正确描述股票价格波动现象及规律的样本函数模型,为解决金融市场中资产定价、最优配置、风险管理及金融监管等实际问题提供了正确的数学模型及方法。
一、引言
金融数学是一门运用数学模型及方法,研究和揭示金融资产价格数量关系及其变化规律,并解决金融市场中资产定价、最优配置、风险管理及金融监管等实际问题的应用数学理论。金融数学的历史最早可追溯到1900年法国巴黎大学巴舍利耶(Bachelier)的博士论文《投机理论》,巴舍利耶首先使用概率方法来研究股票价格波动现象,并将随时间变化的股票价格看作一个增量独立的随机过程,构建出随机游走模型来描述股票价格随时间的变化过程,根据中心极限定理推导出了股票价格服从正态概率的结论。巴舍利耶的研究不仅标志着金融数学理论的诞生,而且也为后来金融数学的发展提供了“将股票价格假设为随机变量”的研究方法。1952年,马科维茨(Markowitz)使用随机变量的均值和方差分别描述证券投资的收益和风险,建立了引发“第一次华尔街数学革命”的组合投资理论,马科维茨因在金融数学领域的开创性工作,获得了1990年诺贝尔经济学奖。1973年,布莱克(Black)和斯科尔斯(Scholes)基于几何布朗运动模型,推导出了著名的B-S期权定价公式,带动了金融衍生品市场的快速创新发展,引发了“第二次华尔街数学革命”,金融数学的理论大厦就此在随机变量假设的基础上建立起来。
金融数学在金融市场的应用,使金融市场获得了空前规模的发展,但是也造成了人类历史上最大的金融体系崩溃。人们从众多的案例分析中得出结论:金融数学建立的股票价格模型并不能正确描述股票价格的波动现象及规律,金融数学在金融领域的应用是失败的,金融数学因此陷入了严重的学科危机(高宏,2021)。本文从随机变量和随机过程的定义出发,分析了金融数学在建立股票价格模型时,将股票价格与时间之间的数量关系假设为随机变量的基本概念错误,无形中改变了股票价格的定义域,导致研究对象从一个样本函数改变为样本函数的集合,从而推导出了“股票价格服从对数正态分布”这一与事实不符的错误结论。本文将股票价格与时间之间的数量关系还原为时间函数,根据“股票价格的对数收益率为白噪声序列”的实证研究结果,建立了可正确描述股票价格波动现象及规律的样本函数模型。
二、概率论中的随机变量定义
随机变量是概率论中一个极为重要的基本概念,也是研究随机现象的基本工具。引入随机变量的主要目的是:把随机试验的结果数量化,将随机事件的结果映射为实数,这样就可以利用数学分析方法来研究随机现象。
随机变量的定义涉及随机试验、样本点和样本空间三个基本概念。随機试验是指人们对随机现象进行的观察或观测,随机试验具有以下3个特征:一是可重复性。在相同条件下可重复进行;二是多结果性。试验结果不止一个,但所有可能的结果都是事先明确可知的;三是不确定性。每次试验之前不能确定会出现哪一个结果,但可以肯定会出现上述所有可能结果中的一个。
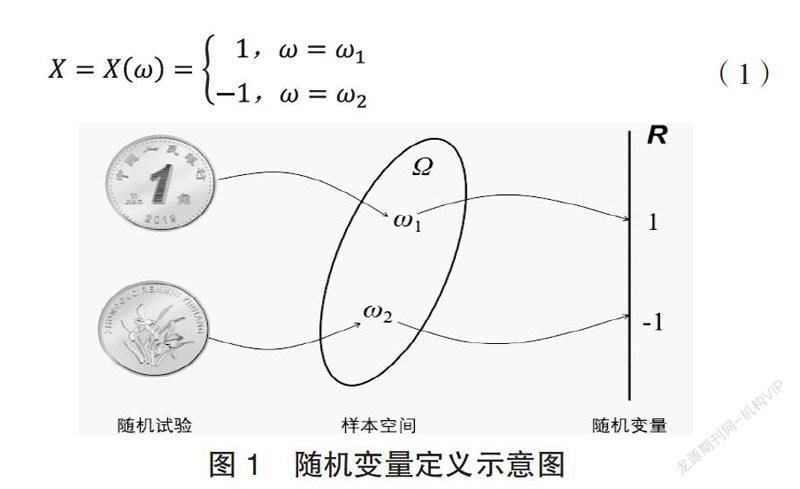
尽管一次随机试验将要出现的结果是不确定的,但其所有可能结果是明确的。我们把大量重复随机试验会出现的每一种可能的结果称为一个样本点,一般记为ω;全部样本点的集合称为样本空间,一般记为Ω。
定义:设随机试验的样本空间为Ω={ω},若X(ω)为定义在样本空间Ω上的单值实数函数,则称X(ω)为随机变量,简记为X。
随机变量的取值可以是连续的,也可以是离散的,根据随机变量取值的不同,可以分为连续型随机变量和离散型随机变量。
通常用大写英文字母X,Y,Z,…来表示随机变量,用小写英文字母x,y,z,…表示实数。如果随机试验的结果本身就是一个实数x,即样本点ω本身是一个实数,这时常定义X= X(ω)= ω= x。
对于抛硬币试验,试验结果可能是硬币正面向上,也可能是硬币反面向上,即有两种可能的结果,而且只有这两种结果,事先可以明确。因此该试验所对应的样本空间Ω由ω1和 ω2两个样本点构成,我们指定实数1和-1分别与样本点ω1和 ω2对应(图1),则随机变量可写成:
从上述随机变量的定义可以看出,随机变量X的取值由样本点ω决定,也就是说,随机变量X是样本点ω的函数,即有X= X(ω),因此,随机变量的定义域为样本空间Ω。
随机变量实质上是一个定义在“随机试验所有可能结果集合”上的单值实数函数,随机变量的不同取值与随机试验的所有可能结果一一对应,随机变量的值随试验结果的不同而变化。从数学上讲,随机变量就是一个从随机试验结果的集合到实数集的映射。
三、随机过程与随机变量的关系
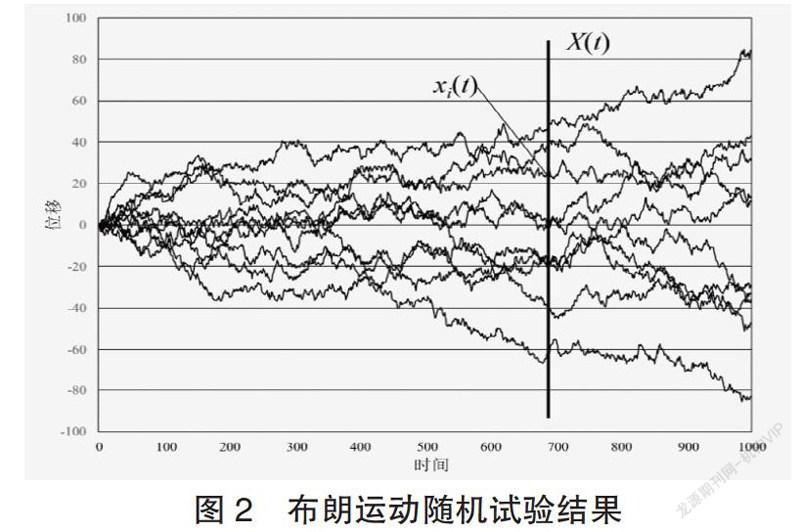
在现实世界中,许多随机现象都是随着时间的进程而变化发展的,这类动态随机现象就是所谓的随机过程。例如在相同条件下重复10次观察一个从原点出发的布朗粒子位移x随时间t的变化过程,可得到图2所示的10条布朗粒子位移曲线,这10次测量结果也可分别用10个时间函数x1(t),x2(t),…,x10(t)表示。尽管每次的试验结果各不相同,但每次的结果却是一个确定性的时间函数xi(t)。若同时观测10个从原点出发的布朗粒子位移x随时间t的变化过程,也会得到与图2类似的试验结果曲线。
显然,对每个布朗粒子的观测结果均为一个随时间变化的实数,亦即随机过程的试验结果是一族时间函数x1(t),x2(t),…,xi(t),…,也就是说,随机过程试验的样本点ωi与时间函数xi(t)一一对应(图3)。

