SVPWM教学研究之空间矢量冲量等效原理
佘 焱, 王 勇, 孙 佳, 徐青菁
(上海交通大学 电力传输与功率变换控制教育部重点实验室,上海200240)
0 引言
空间电压矢量脉宽调制SVPWM将电压型逆变器输出的基本空间电压矢量合成需要的空间电压矢量,是逆变器控制的重要技术[1],在电机控制和并网技术等领域中有重要应用。但是,我们在SVPWM教学中,发现有些难点目前很少有资料进行讨论,特别是SVPWM的理论基础,本文进行了一些探讨和澄清,在此求教于大家。
1 冲量等效原理
空间矢量脉宽调制将逆变器输出的基本空间矢量合成参考空间矢量,合成的理论基础目前很少有资料提及或者讨论。本节首先证明冲量等效原理,再推广到三相三线制电路的线电压冲量等效原理。
定理1(冲量等效原理):设开关周期Ts足够小,幅值为vi的电压脉冲的宽度分别为Ti,Ti≤Ts,i=1,2。且
v1·T1=v2·T2
(1)
则,v1和v2是通过惯性环节的响应等效。
证明:设惯性环节如图1所示:
显然:
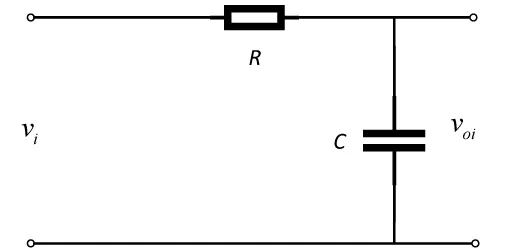
图1 惯性环节
容易证明,上述电路的冲激响应为:
(2)
输入幅值为vi,宽度为Ti的电压脉冲,则响应为:
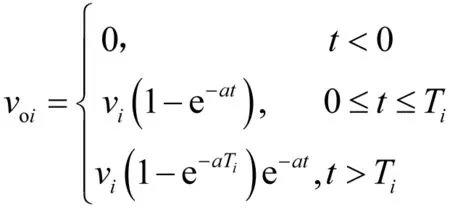
(3)
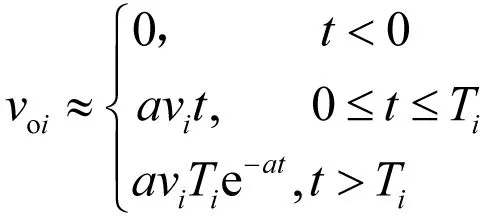
(4)
由式(1),v1·T1=v2·T2,所以,由式(4),当t>Ti,响应完全相同,考虑到Ti足够小,可以近似认该惯性环节具有相同响应。
推论1:设开关周期Ts足够小,幅值为vi(i=1,2,3)的电压脉冲的宽度分别为Ti,其中T1+T2≤Ts,T3≤Ts。且
v1·T1+v2·T2=v3·T3
(5)
则,v1和v2在一个开关周期内相继通过惯性环节的响应与v3通过该惯性环节的响应等效。
证明:由定理1的证明,特别是式(4),如果单独输入信号vi(i=1,2,3),则当t>Ts>Ti时,响应的值与脉冲的面积成正比。当v1和v2在一个开关周期内相继输入线性系统时,系统的响应为分别输入v1和v2的响应之和,由式(5),该响应等于v3的响应。
推论2:设开关周期Ts足够小,三个线电压脉冲,幅值分别为vUVi,vVWi,vWUi(i=1,2),宽度分别为Ti,Ti≤Ts。且
vUV1·T1=vUV2·T2
vVW1·T1=vVW2·T2
vWU1·T1=vWU2·T2
则,vUV1,vVW1,vWU1和vUV2,vVW2,vWU2通过三线三相电路对称惯性环节的响应等效。
证明:设三线三相电路对称惯性环节如图2所示。其中
R1=R2=R3=R
C1=C2=C3=C
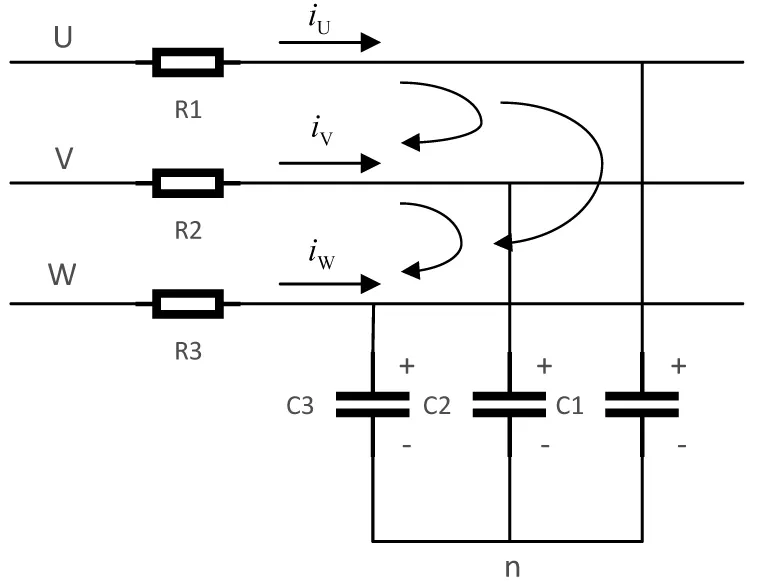
图2 三线三相电路对称惯性环节
考虑图示三个回路,由基尔霍夫电压定律:
vUV=vC1-vC2+R1iU-R2iV
vVW=vC2-vC3+R2iV-R2iW
vWU=vC3-vC1+R3iW-R2iU
注意到:
将上式代入式(),
记输出线电压:
v12=vC1-vC2
v23=vC2-vC3
v31=vC3-vC1
得:
注意到输入线电压和输出线电压满足和定理1中输入输出电压完全相同的微分方程,所以,完全类似的方法可以证明推论2.
推论3:设开关周期Ts足够小,三个线电压脉冲,幅值分别为vUVi,vVWi,vWUi(i=1,2,3),宽度分别为Ti,其中T1+T2≤Ts,T3≤Ts。且
vUV1·T1+vUV2·T2=vUV3·T3
vVW1·T1+vVW2·T2=vVW3·T3
vWU1·T1+vWU2·T2=vWU3·T3
则,vUV1,vVW1,vWU1和vUV2,vVW2,vWU2在一个开关周期内相继通过三线三相对称电路惯性环节的响应与vUV3,vVW3,vWU3通过该惯性环节的响应等效。
证明:根据推论2的建模,类似推论1可以证明。
2 空间矢量的冲量等效原理
2.1 空间矢量

图3 三相电压的空间矢量
定义[2]对于给定的三相电压vU、vV、vW,称

(6)
为三相电压vU、vV、vW的空间矢量,其中k为常数。上述求和为矢量求和运算。
容易证明,式(6)等价于:

(7)
2.2 空间矢量的冲量等效原理
定理2(空间矢量冲量等效原理):设开关周期Ts足够小,三相相电压vUi、vVi、vWi(i=1,2,3)的空间矢量分别为Vi(i=1,2),Vi的输出时间分别为Ti,其中Ti≤Ts。且
证明:由式(7):
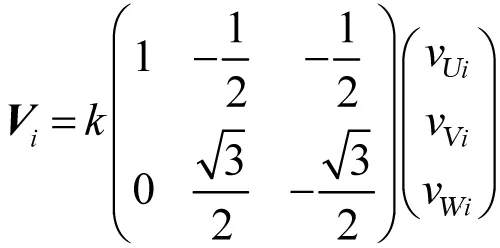
(9)
式(9)代入式(8),得

适当简化:
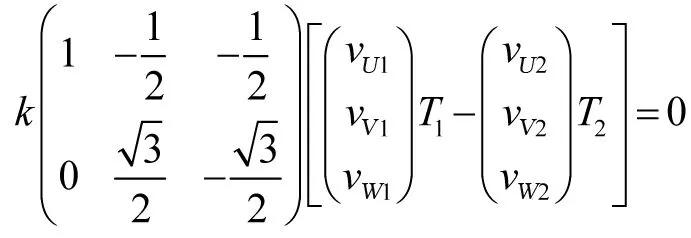
进一步简化:
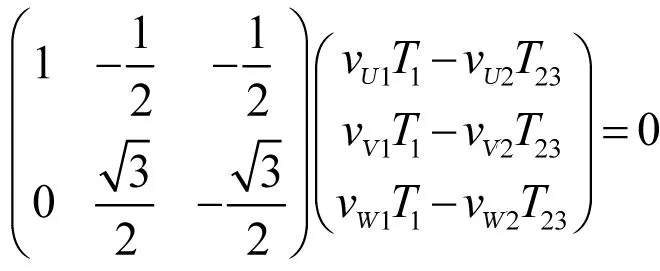
由上式可得:
vU1T1-vU2T2=vV1T1-vV2T23=vW1T1-vW2T2
由上式可推出:
(vU1-vV1)T1=(vU2-vV2)T2
(vV1-vW1)T1=(vV2-vW2)T2
(vW1-vU1)T1=(vW2-vU2)T2
记vUVi-vUi-vVi,vWVi-vVi-vWi,vWUi-vWi-vUi,由推论2得证。
推论4:设开关周期Ts足够小,三相相电压vUi、vVi、vWi(i=1,2,3)的空间矢量分别为Vi(i=1,2,3),Vi的输出时间分别为Ti,其中T1+T2≤Ts,T3≤Ts。且
V1·T1+V2·T2=V3·T3
(10)
则,V1和V2在一个开关周期内相继通过三线制对称电路惯性环节的响应与V3通过该惯性环节的响应等效。
证明:由式(7):

(11)
式(11)代入式(10),得

适当简化:
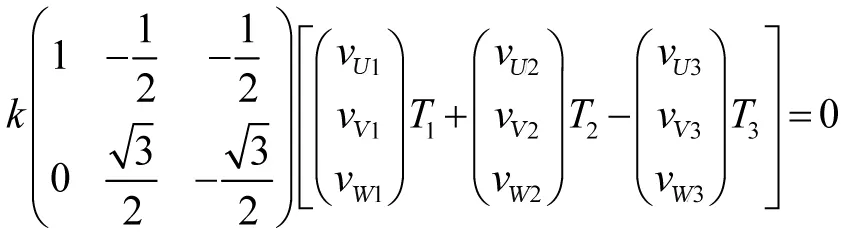
进一步简化:
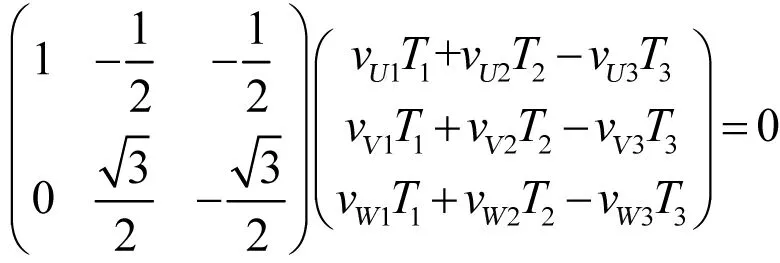
由上式可得:
vU1T1+vU2T2-vU3T3=vV1T1+vV2T2-vV3T3=vW1T1+vW2T2-vW3T3
由上式可推出:
(vU1-vV1)T1+(vU2-vV2)T2=(vU3-vV3)T3
(vV1-vW1)T1+(vV2-vW2)T2=(vV3-vW3)T3
(vW1-vU1)T1+(vW2-vU2)T2=(vW3-vU3)T3
记vUVi=vUi-vVi,vVWi=vVi-vWi,vWUi=vWi-vUi,则推论3得证。
3 结语
本文提出并证明了SVPWM的理论基础空间矢量的冲量等效原理,对于学生透彻理解掌握SVPWM有重要意义。

