基于知识体系结构的组卷方法研究与应用

乔亚男， 程 航， 薄钧戈

(西安交通大学 计算机科学与技术学院，陕西 西安 710049)

0 引言

大学计算机类课程是非常重要的高校公共基础必修课程，该类课程以计算思维培养为目标，在教学内容中渗透计算思维的基本理念，为学生展示计算机学科的轮廓和相关技术，提升学生利用计算机解决本专业应用问题的能力，同时为未来可能的学科交叉研究打下基础。基于计算机学科的自身特点，在培养高素质专门人才和拔尖创新型人才的大背景下，推动教学评价改革成为计算机基础课程教学改革的重中之重。随着高校校园网建设的不断完善，考试的方式、载体发生了比较大的变化，由传统的线下考试转变为无纸化线上考试，经过长时间的考试在电子化试题库中积累了相当量的试题，传统人工组卷方式不仅耗时耗力、效率低下，并且不能保证所组试卷科学合理[1～2]。

自动组卷是指根据出题人所指定的约束条件，从题库中自动筛选满足条件的试题，从而代替人工选题的过程[3]。大学计算机类课程包含数门课程，涉及软硬件系统、网络、数据库、程序设计、多媒体技术等众多知识点，不同课程的考核范围既不同又有一定交叉。并且正常教学活动中，组织一门课程的考试通常要准备数份甚至数十份试卷。这些特点决定了计算机自动组卷若要满足教学需求必须解决以下几个问题：①如何保证多份试卷在难度、结构、考核范围等方面一致；②如何提高算法性能。

近年来，已有多位学者针对组卷问题开展自动组卷方法研究。目前的自动组卷方法主要分为三大类：第一类为借助于某种随机算法进行组卷,如Marzukhi和Kiran对传统随机抽题算法进行了改进，利用洗牌算法避免了重复性抽题[4～5]。第二类是基于深度优先搜索算法DFS(Depth-first Search)或者广度优先搜索算法BFS(Breadth-first Search)进行组卷，如陈雷等人[6]针对回溯抽题算法时间复杂度和空间复杂度较大的问题进行了改进，提出了“目标终止回溯试探法”和“缩减深度回溯试探法”，在实验中证明了两种算法在特定试题库中提高了组卷效率，但所组试卷中仍有部分重复试题，并且算法适应情况较窄。最后一类则是借助于智能启发式搜索算法进行组卷,如Zhang等人[7]在试题库建设中使每种题型在数据库中对应一张表，并在原始仿生学遗传算法中对初始种群的生成采取了约束，采用实数编码代替了传统的二进制编码，提高了算法的收敛度。Hu等人[8]将遗传算法与粒子群算法两种算法相结合，通过实验数据分析了影响组卷的因素。此外，基于遗传算法和蚁群算法，国内多位研究者在智能考试和组卷算法上也进行了深入的研究[9～11]。

针对上述存在的问题，本文通过对组卷问题建模，对自动组卷中的难点问题进行深入研究，对传统随机抽取算法进行了改进，提出了一种针对大学计算机类课程知识体系结构的自动组卷方法。

1 设计思想

1.1 题库参数设计

题库是选择组卷算法及能否实现组卷的关键因素，一个好的题库设计在一定程度上可以提高算法的执行效率。

在试题表中，每道试题题干、答案以XML格式储存，特别地，当题型为编程题时，额外拥有测试用例字段，该字段也以XML格式存储。根据组卷要求，每道试题Qi拥有多个约束属性，包括难度、题型、知识点、章节等，具体可表示为式(1)。

Qi= (QIDi,CIDi,Ti,Si,Pi,Di,...)

(1)

QIDi作为主键表示当前的试题编号，是每个试题的唯一标识，CIDi表示此试题对应的课程编号，作为外键与课程表相关联，Ti表示该试题的题型，Si表示该试题在相应课程编号下对应的章节，Pi表示该试题在对应课程对应章节下的所属知识点，Di表示该试题的难度等级。其中试题的难度系数与难度等级对应关系，如表1所示。

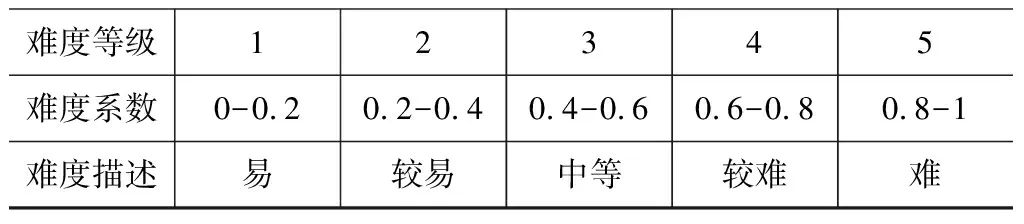
表1 难度等级与难度系数对应关系

在数据库中，将试题的题型以int类型存储，以提高检索效率。试题的题型表示与题型描述对应关系如表2所示。

表2 题型对应关系

在知识点标注时，采用分段实数编码的方式，具体可表示为式(2)。

Pi=CIDiSiKi

(2)

其中，CIDi表示该知识点对应的课程编号，Si表示该知识点对应的章节，Ki表示为该知识点的序号。例如：450102,45则为编号为45的课程，01代表该课程的第一章，02代表该课程第一章的第二个知识点。

1.2 候选试题数据结构

组卷时，系统根据用户所设定组卷需求预先将数据库中的试题信息自动读入内存中，生成供随机选题用的候选试题数据结构。

抽题算法主要数据结构包括两个部分，第一部分为章数组字典IDAndChapter，数组下标代表题型，每个字典中的键值对代表试题编号与章的对应；第二部分为知识点数组字典IDAndKP，数组下标代表题型，每个字典中的键值对代表试题编号与知识点的对应。

2 组卷算法描述

采用此方法组卷的一般过程如下：

(1)根据组卷条件，判断当前题库情况是否满足组卷要求，若满足条件则开始组卷；否则重新设置组卷参数；

(2)采用一种基于知识体系结构的改进型随机抽取算法，依次循环为各试卷抽取指定题型中之前未被抽取过的题目，直到抽取完条件要求的全部题目；

(3)题目抽取完成后，计算各试卷中每类题型的平均难度值，确定是否符合设定要求。如果不符合，则采用一种循环替换算法进行难度值调整，直到满足设定要求。整体流程如图1所示。

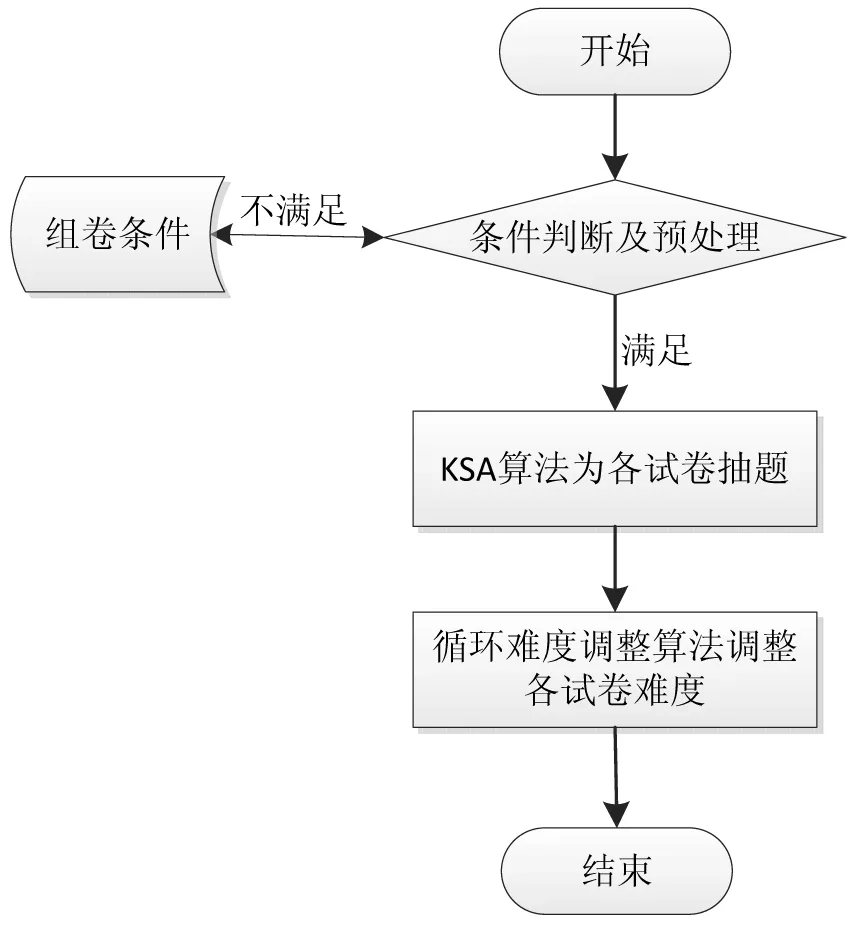
图1 组卷整体流程图

2.1 条件判断及预处理

根据用户所设置组卷条件，判断当前题库试题是否满足组卷要求，若满足条件则进入下一步开始组卷，否则重新设置组卷参数。这里的组卷条件可通过浏览器登录组卷系统设置。包括的参数有：

(1)课程(Course)：本次组卷针对的具体课程；

(2)试卷数量(PaperNum)：需要同时组成的试卷套数；

(3)考核范围(Scope)：试题涉及的章范围；

(4)题型(QType)：各试卷所包含的题目类型。题型包括：单选、多选、判断、填空、问答、编程、综合。

(5)每种类型题目数量(QTNum)：每套试卷中单种题型的题目数量。

(6)题目分值(Score)：每种题型的单道题目分值。不同题型的单道题目分值可以不同。

(7)题型难度值(QDegree)：试卷中每种类型题目的平均难度值。不同题型的QDegree可以不同。

其中，“试卷数量”是指同时组成的试卷数，该数量与实际需要及题库容量有关。在Scope设定的前提下，若用Sumf表示用户所设置的试卷总分值，SumS表示题库中设定考核范围的总题量，Sumt表示题库中考核范围内任意一种题型的题目数量，n表示要求的题型种类数，对同时组成的每套试卷，其n值相同。则允许同时组成的试卷数量应同时满足公式(3)、公式(4)和公式(5)，否则需要重新调整组卷参数。

(3)

(4)

Sumt≥PaperNum×QTNum

(5)

其中，公式(3)的含义是：每套试卷总分值应与用户所设置试卷总分值相等；公式(4)的含义是：题库中指定考核范围的试题总量应大于等于所需试卷题目数量之和；公式(5)的含义是：题库中每种题型的题目数量应大于等于所需试卷每种题型题目数量之和。

2.2 基于知识体系结构的抽题算法

这里的知识体系归属于计算机教学领域，其结构包含课程(Course)、章(Scope)、知识点(Point)及相互之间的对应关系，课程、章、知识点是特定领域约定俗成的术语，三者为包含关系，满足如下表达式(6)。

Point⊆Scope⊆Course

(6)

按照公式(6)可得计算机领域知识体系拓扑结构图，包含：课程(Course)、章(Scope)、知识点(Point)，它们之间满足公式(6)所述关系。拓扑结构图如图2所示。

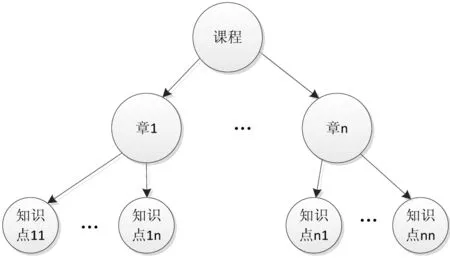
图2 计算机领域知识体系拓扑结构图

定义二维数组MIsChoosed和PIsChoosed，分别表示某类题型中某章是否已抽取，以及某章中某知识点是否已抽取；定义整型变量Count表示某题型已抽取的题目数量，初始化为0；定义Sum表示某类题型所需题目数量。具体流程为：

(1)选定准备抽取的题目类型；

(2)选择已抽取章的下一章(初始时默认为第1章)作为当前抽取章，采用算法2依次为各试卷抽取一道题目。

(3)判断各试卷该题型题目数量是否达到要求，如果没有，则继续(2)。否则进行过程(4)

(4)判断是否所有题型题目均已抽取完毕，如果没有，继续(1)，选择下一种题型；否则，表示各试卷所有题型题目都已抽取完毕。

所有试卷抽题流程算法伪代码如下所示。

1)算法1

输入：某课程下所有试题QIdList，组卷约束条件。

输出：所组多份试卷paperList。

//i为当前题型

For each i [0,6] do

Define Count = 0

While (Count < Sumi) do

//chaps为用户所选定章节

For each chap chaps

KSA();//算法2

End while

End for

Return paperList

其中，一次为每套试卷抽取一题的算法思想为：根据图1所示领域知识体系，在已构建领域知识体系基础上，按照章及章内知识点顺序，遵循未被抽取过题目的知识点优先原则，依次循环为各试卷抽取指定题型中之前未被抽取过的题目，直到抽取完条件要求的全部题目，详细步骤如下算法所示。

基于知识体系结构的改进型随机抽取算法

输入 某课程下所有试题QIdList，组卷约束条件。

输出 符合出题人设定的多份试卷paperList。

步骤1：判断当前抽取章curChap中当前题型i是否还有未被抽取过的题目，若全部题目均已被抽取，则进入步骤4；否则，基于知识体系结构，从该章中按顺序选择一个知识点curKP，执行步骤2；

步骤2：判断该知识点是否有未被抽取过的该题型题目。若有，执行步骤3；否则，选择该知识点所对应章节的下一个知识点，重新执行步骤2；

步骤3：从选定的知识点中随机抽取一道未被抽取过的题目QId；

步骤4：选择下一章作为当前抽取章(初始时默认抽取第一章)，若全部章被抽取完，则将所有章置为未抽取状态，选择第一章作为当前抽取章，重新返回步骤1；

步骤5：判断各试卷是否均已抽取一道指定题型的题目，如果没有，转向步骤2；否则，将所抽取的题目及其知识点标记为“已抽取”，将包含该知识点的章设为已抽取章。完成为每套试卷抽取一道指定题型题目工作，伪代码如算法2所示。

2)算法2

输入：某课程下所有试题QIdList，组卷约束条件。

输出：所组多份试卷paperList。

Define paper = 0 ;//当前试卷

If(!Mischoosed[chap]) do

//KPs为当前章下所有知识点

Define KPs getKPs(chap)

For each kp KPs do

If(!PisChoosed[i][kp]) do

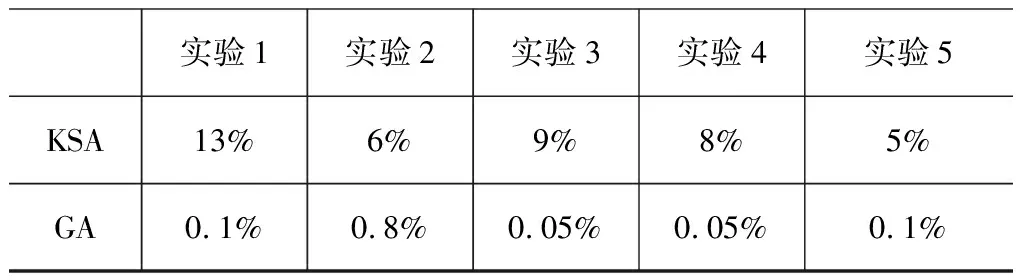
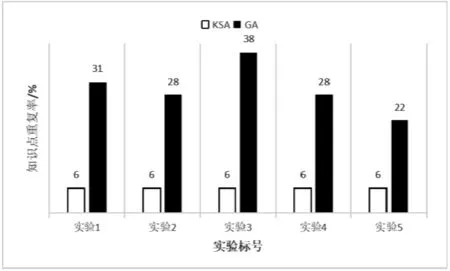
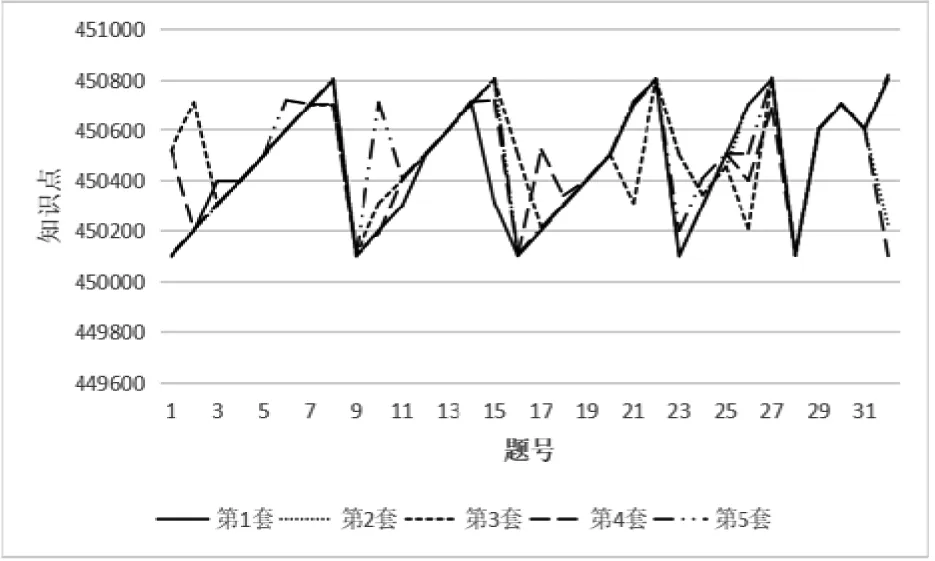
While(paper

QId Random();

PisChoosed[i][chap] = True;

MisChoosed[chap] = True;

paperList[paper].add(QId);

End while

paper = 0;

End if

End for

End if

2.3 循环难度调整算法

对按照算法1所抽取的各试卷，分别计算各试卷中每类题型的平均难度值，并与用户所设定的各题型难度值进行比较，判断某试卷某题型的平均难度值与该题型对应难度值偏差是否处于允许范围内。若不符合，则采用一种循环难度调整算法遵循知识点、章、其它章的搜寻顺序进行试题难度调整，直到满足设定要求。

设Dai为表示第i套试卷选定题型的平均难度值，Di为该题型设定难度值，f为允许误差值，参照算法2，试卷难度调整的具体方法为：

输入 基于上述抽题算法的所组试卷paperList

输出 符合用户所设定难度的试卷paperList`

依次处理paperList中的每套试卷，以第一份试卷为例，按序选定试卷题型，计算该试卷该题型的平均难度值Dai，并与该题型设定难度值Di进行比较，则有以下三种情况：

(1)如果|Dai-Di|

(2)如果|Dai-Di|≥f且Dai>Di，则删除第i套试卷该题型中难度值最大的题目，重新抽取难度值较小、且在本次组卷中未被抽取过的同类型题目替换，直到满足要求为止。

(3)如果|Dai-Di|≥f且Dai

所诉情况(2)的循环难度调整算法包括如下具体步骤：

步骤1：删除该题型当前难度值最大的题目MaxQId，从题目属性中获取待替换题目关联的知识点MaxQIdKP，查找题库中同一知识点中是否有未被抽取过、难度值小于被删除题的同类型题目。若有，则执行步骤5，否则继续步骤2；

步骤2：从包含该知识点的章中查找是否有未被抽取过、难度值小于被删除题的同类型题目。若有，则执行步骤5，否则继续步骤3；

步骤3：从其它章中查找是否有未被抽取过、难度值小于被删除题的同类型题目。若有，则执行步骤5，否则继续步骤4；

步骤4：按照上述原则仍没有找到符合条件的题目，则难度调整失败，重新组卷。

步骤5：随机抽取一道满足条件的题目ranQId替换原题。计算当前题型的平均难度值，若符合难度范围要求，则结束；否则继续转向步骤1。

所述情况(3)采用类似的循环难度调整算法，依次替换题型中难度值最小的题目，直到该题型难度值满足要求。

当所有题型均满足|Dai-Di|

3)算法3

输入：基于前述改进型随机抽题算法的所组试卷paperList。

输出：经难度调整的paperList`。

Define f

For each curQType [0,6] do

//i为当前试卷

For i= 0;i

If(|Dai-Di|

Continue;

While(|Dai-Di|≥f&&Dai>Di)do

paperList[i].remove(MinQId)

ranQId Random();

paperList[i].add(ranQId);

End while

While(|Dai-Di|≥f&&Dai

paperList[i].remove(MaxQId)

ranQId Random();

paperList[i].add(ranQId);

End while

End for

End for

Return paperList`

3 实验过程及分析

3.1 实验条件

为了验证本课题所提出的基于知识体系结构组卷算法KSA(knowledge structure algorithm)的有效性，采用“大学计算机基础”这一课程题库作为测试数据，题目数量共计803道，其中单选题318道，多选题32道，判断题134道，填空题169道，程序题130道，综合题20道。

测试环境：

1)软件环境

操作系统：Windows 7 64bit

开发语言：C#+HTML+JavaScript

开发环境：Microsoft Visual Studio 2017

数据库：Sql Server 2012

浏览器：Google Chrome

2)硬件环境

CPU：Intel(R) Core(TM) i5-4590 CPU @ 3.30GHz

RAM：8G

3.2 试卷参数

(1)课程：大学计算机基础。

(2)章范围：第1-8章。

(3)试卷总分：100分。

(4)试卷题型及各题分值：单选题16题，每题2分，共计32分；判断题10题，每题2分，共计20分；填空题2题，每题7分，共计14分；编程题3题，每题8分，共计24分；综合题1题，每题10分，共计10分。各题型难度值设定除判断题题型为2，其余题型均为3。

(5)组卷份数：5份。

3.3 实验结果及分析

应用本文提出的KSA组卷算法与传统遗传算法GA(genetic algorithm)在组卷效果与执行效率上进行了对比实验，每个算法实验共进行5次，每次均以上述试卷参数为基准进行组卷。以实验中试卷的难度值方差来衡量各试卷难度的离散程度，以限定题目数量下的知识点重复率衡量多套试卷知识点的重复情况，以各试卷间知识点走势及拟合程度衡量知识点平衡情况，以算法执行时间衡量算法性能。对比实验结果如下所示。

1)两种算法难度值方差对比

每次实验的难度值方差说明了各试卷之间难度的偏离程度，该方差数值越小，代表多份试卷难度基本持衡。两种算法难度值方差对比实验数据如表3所示。

表3 难度值方差对比实验

从表中可以看出，KSA算法的方差值高于GA，主要原因是：GA算法中种群进化时会优先挑选适应度高的个体进入下一代，在不断的杂交之后，种群多样性锐减，导致个体相似度过高，即试卷中试题重复率过高，故所组试卷之间难度值方差极小。

2)两种算法知识点重复率对比

在一份质量较高的试卷中，每道试题应有对应的知识点且互相不重复。这里题库中的知识点标注以该题最想考察的知识点为主。取每次实验中重复率最高的试卷作对比，对比结果如图3所示：

从图中可以看出，以KSA算法所组试卷的知识点重复率远低于GA，最大差值为32%，提高了试卷的质量。

图3 难度值方差对比实验

3)知识点走势及拟合程度

分别以KSA算法和GA算法为核心所组试卷中随机抽样一次实验进行分析，图4给出了32道题目同时组5份试卷的章、知识点分布情况。

(a)KSA知识点走势及拟合程度

(b)GA知识点走势及拟合程度图4 知识点重复率对比实验

由上图可以看出，图(a)较之于图(b)，5份所组试卷的知识点曲线走势更趋于拟合，这说明了KSA算法在组多份试卷的情况下能够考虑到试卷之间的知识点平衡关系，为考试提供了一定的公平性。但从上图也可以看出，在个别题目上曲线走势分歧较大，如：1-3题、9-11题，主要原因是：该知识点下没有足额未抽取的试题以供组卷。当组卷数目大于某知识点下题目总数时，KSA算法会优先抽取该知识点下试题，剩下的差额试题会自动从下一个知识点下抽取，当该章下所有知识点均标记为已抽取状态，则从该章的下一章抽取。

4)算法性能对比

以组卷执行时间代表算法性能，由图5可以看出两种算法性能大致一般，组卷时间在2s内，满足高校教师的需求。

图5 知识点走势对比实验

由以上所有对比实验可知，本文与传统的遗传算法相比，极大的降低了知识点的重复率，利用预定义的字典数组MIsChoosed和PIsChoosed实现了筛选试题无重复。实际运用中，组卷时间和体验符合高校教师的基本组卷需求，基于知识体系结构的随机抽取算法在组卷系统中得到了成功的运用。

4 结语

组卷是试题库建设和在线考试系统的核心内容，设计一种高效、科学、鲁棒的组卷算法则是重中之重。本文针对现有算法未考虑组多份难度一致、知识点均衡试卷的情况而提出基于知识体系结构的随机抽取算法和循环难度调整算法，全面考虑知识点、难度控制，组卷结果更加符合正常的教学活动。在与传统遗传算法的对比实验中，表现出了更好的组卷效果。

基于本文方法开发的题库管理系统和考试系统已经在西安交通大学的教学环境中得到了实际应用，提升了教学体验，得到了师生的一致好评，我校“大学计算机”系列课程，最近几年相继被评为国家级“一流课程”，和该部分的教学改革是分不开的。首先，按照知识点比例进行考试题目分布，对教师的教学和学生的学习都有了更高的要求，通过对平时习题和考前模拟的综合分析，教师可以充分了解学生对知识点的掌握情况，对知识点进行有针对性的讲解，达到提升教学质量的目标。而学生在反复练习的过程中，也可以查漏补缺，优化解题思路，巩固知识点掌握。其次，通过对知识点的全面覆盖，也可以确保考试公正，避免学生复习的片面性，降低考前“押题”、“猜题”的收益率，提升学生学习水平和考试成绩的相关性。

虽然实际测试结果已表明本文方法优于传统遗传算法，但还存在着一些欠考虑的情况，如：是否可以继续降低知识点重复率，是否可以在大型题库中快速组卷。这些还需要进一步的实验以完善算法。