动初级高速六相直线感应电机工作特性分析

韩 一，聂子玲，许 金，朱俊杰

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

直线电机由旋转电机演变而来，是一种能够实现将电能直接转换为直线运动的机械能的电力传动装置。近年来，随着大功率电能变换及高能量密度脉冲储能技术的突破，使得利用直线电机将存储的电能瞬间转化为高速动能成为可能。其中，动初级(短初级)六相直线感应电机(Linear Induction Motor，LIM)避免了分段供电技术带来的系统繁杂、可靠性低、电缆压降大等问题，且具有多相电机提高系统冗余度、控制自由度及功率密度等优势，有较高的研究价值，且在电磁发射领域、汽车碰撞实验等场合有广阔的应用前景[1-2]。

直线电机的建模及其工作特性是电磁设计、控制策略、效能评估的重要依据。与旋转电机相比，直线电机的模型分析需要考虑边端效应。其中，动态边端效应是电机初级与次级相互作用所产生的电磁瞬态现象，在动初级直线感应电机运行过程中体现得较为明显。相关文献对动初级直线感应电机的建模及分析方法进行了研究，主要包括基于麦克斯韦方程组的电磁场分析法[2-6]、基于等效电路的集总参数法[7-14]以及有限元法[15-16]。通常，前两种方法用于电磁设计、模型推导及性能计算，第三种方法则用于模型验证。

文献[2]基于一维、二维电磁场理论，计算了直线感应电机在边端效应影响下复杂气隙磁密分布表达式。文献[5]基于电磁场分析法研究了动态边端效应影响下电机推力特性，结论指出动态边端效应会造成电机正向推力下降，且随速度的增大，推力下降趋于严重。文献[6]给出了六相筒式直线感应电机自然坐标系下的模型并基于端部脉振磁场推导得到了电机的不对称电感矩阵。

在旋转感应电机等效电路的基础上，直线感应电机通过参数修正的方式引起横、纵向边端效应，半填充槽等现象[7-12]。文献[7-8]通过电磁场方程推导，引入4个修正系数，建立了同时考虑横、纵向边端效应的单边直线感应电机数学模型。文献[12]引入无量纲系数Q，推导了激磁电感随Q变化的函数，并建立了考虑动态边端效应的直线感应电机等效电路。为了提高模型的准确性，文献[13]将感应涡流等效为电容充放电的过程，提出了计入次级漏感影响的边端效应修正系数，但推导过程极为复杂，且次级等效电路中的电容没有实际物理含义。目前，动态边端效应的分析和修正方法得到了该领域学者的认可，且实际运用更多的是文献[2，7]提出的基于电磁场方程推导和文献[12]提出的基于无量纲系数Q的修正方法。其中，后者因其物理概念清晰，推导过程简单的优点，更适合运用于直线感应电机的实时控制，但模型刻画的准确度不如前者。

本文以工作于非周期瞬态工况的动初级六相直线感应电机为研究对象(级数为9，忽略静态边端效应造成的不对称影响[1])，其运行特点为，运行时间短、全程无稳态(无匀速态)、加速度大、动态边端效应明显。为了降低模型的复杂度且兼顾其准确性，采用一阶等效电路分析法分析了动态边端效应影响下电机参数变化特征，并基于涡流损耗推导，建立了考虑动态边端效应的六相直线感应电机数学模型。基于模型对电机进行了性能计算及分析，并通过有限元仿真和实验进行了验证。

1 动态边端效应

1.1 感应涡流定量计算

图1所示为动初级六相直线感应电机动态边端效应示意图。初级运动时，初级绕组在次级导电层上感应出与初级电流大小相等方向相反的涡流，同时，次级导电层会逐渐被其新的部分所替换(图1中B点被A点替换)，由楞次定律可知，新的部分通过入端感应涡流阻碍气隙磁通的瞬时变化。当次级导电层被瞬间替换时，气隙磁通在替换的时间零点消失并随时间的推移上升至其原来的值，相应地，初级在次级导电层上感应的涡流逐渐下降。

图1 动态边端效应示意图 Fig.1 Schematic diagram of dynamic end effect

定义Tr为电机的次级时间常数，Tr=Lr/Rr。其中，Lr和Rr分别为次级回路电感(Lr=Lm+Llr)和电阻。为了定量分析动态边端效应的瞬态过程，设动子(初级)通过定子导电层上一点所需的时间为Tv，则Tv=D/v。其中：D为动子的长度；v为动子的运动速度，动子以次级时间常数为单位运动的距离为vTr。引入无量纲系数Q[12]，Q=Tv/Tr=DRr/vLr，从Q的表达式可以看出，电机的运动速度越快，Q的值越小，气隙磁场越小，表示动态边端效应越严重。

当初级进入次级某个点时，初级绕组在该点感应出涡流，涡流的大小与初级电流相等。实际上，由于次级漏感的存在，会阻碍涡流的瞬变。文献[12]指出，传统三相直线感应电机次级漏感通常仅为激磁电感的5%左右，可忽略其对感应涡流变化的影响。为了更精确得到电机参数的变化规律，建立更准确的数学模型，需要考虑次级漏感对感应涡流变化的影响。如图2所示，将次级等效为一个RL一阶电路，则将初次级相互作用描述为RL电路的瞬态零输入响应的过程。

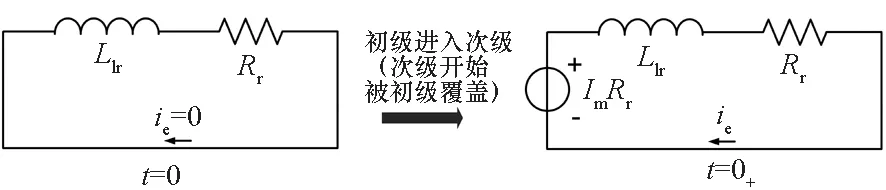
图2 次级感应涡流等效电路Fig.2 Equivalent circuit of induced eddy current

图2中Im和ie分别表示初级电流和次级感应涡流的瞬态值。在t=0+时刻，建立电路的零输入响应微分方程，并考虑感应涡流随次级时间常数衰减，于是感应涡流的表达式为：

ie(t)=Im(1-ep1t)ep2t

(1)

其中，p1=-Rr/Llr为微分方程的特征根，p2=-Rr/(Lm+Llr)。利用式(1)可画出感应涡流瞬态值随时间的变化曲线，如图3所示，图中p.u.为标幺值。由于次级漏感具有阻碍感应涡流瞬变的作用，感应涡流起始阶段并不会突变，而会有一个渐变上升的过程。随着次级漏感的增加，感应涡流在初始阶段上升变缓慢，感应涡流上升的最大值减小。

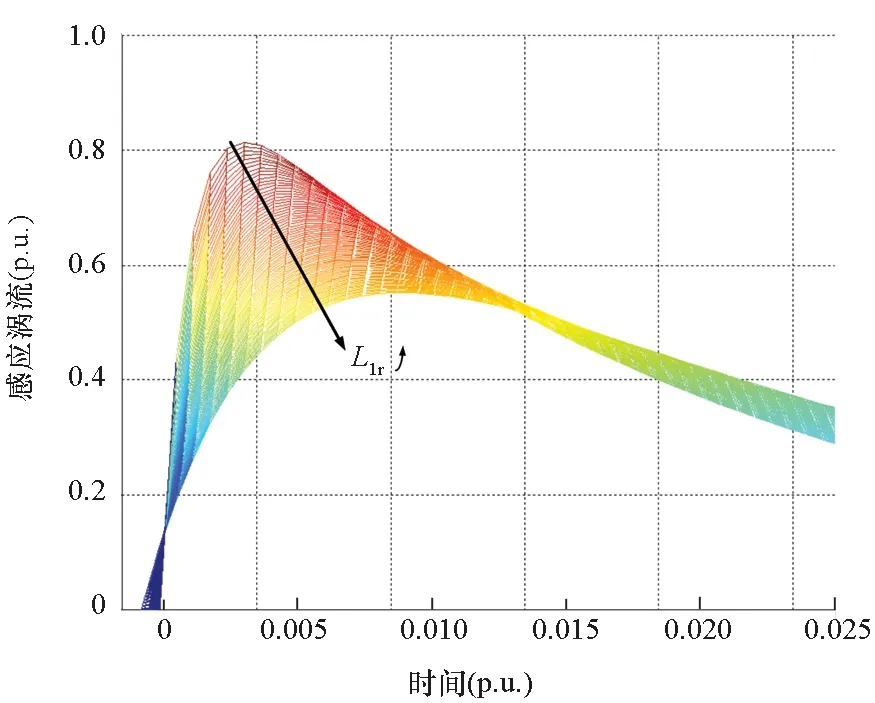
图3 感应涡流变化曲线Fig.3 Variation of induced eddy current

进一步推导，感应涡流的平均值为：

(2)

将p1，p2，Q代入式(2)得到：

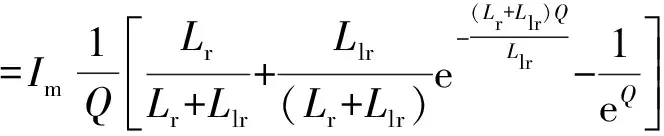
=km(v,t)Im

(3)

其中，km(v,t)的后缀表示该系数随速度时变，简写为km。t1时刻，被感应涡流抵消后的有效励磁电流瞬态值为：

Im(t1)=Im(t0)-Ie_avg(t1)=Im(t0)-kmIm(t0)

(4)

Im(t0)表示励磁电流的初始值，通过式(3)、式(4)可得到t2时刻感应涡流及有效励磁电流的瞬态值，t3、t4,…,tn时刻同理，于是迭代求和得到：

(5)

(6)

1.2 激磁电感时变规律

将感应涡流的去磁效应等效为一个附加的与激磁电感并联的去磁电感。当电机处于静止状态时，励磁电流和激磁电感值分别为Im(t0)和Lm。当动子运动时，流过去磁电感的电流将流过激磁电感的励磁电流分流，其值为感应涡流Ie_avg(t)。根据式(5)、式(6)得到在动态情况下，去磁电感和激磁电感并联后等效激磁电感为：

(7)

其中，kL(v,t)的后缀表示系数随速度时变，简写为kL。kL即为考虑动态边端效应时激磁电感的修正系数，该系数随速度时变。为了对比分析，给出不考虑次级漏感时激磁电感变化的表达式[12]，即：

(8)

为了直观体现激磁电感随速度和次级漏感的变化规律，利用式(7)、式(8)画出其变化曲线，所用到的参数如表1所示(忽略磁饱和效应)。

表1 电机次级参数

如图4所示，记ΔLm1为该情况下考虑漏感和不考虑漏感时激磁电感的差值。可见，考虑次级漏感时激磁电感的下降率相比不考虑次级漏感更小，且ΔLm1随速度的增大而增大。记相同速度工况下考虑和不考虑次级漏感时激磁电感的差值为ΔLm2，随着次级漏感的增加，ΔLm2逐渐增大。图4表明，对于高速、次级漏感较大的直线感应电机，在分析动态边端效应时，必须考虑次级漏感的影响。本文的研究对象在静态情况下，次级漏感约为激磁电感的16%，该比例远大于传统的直线感应电机。因此，为了建立更准确的数学模型，在考虑动态边端效应时，需计入次级漏感的影响。

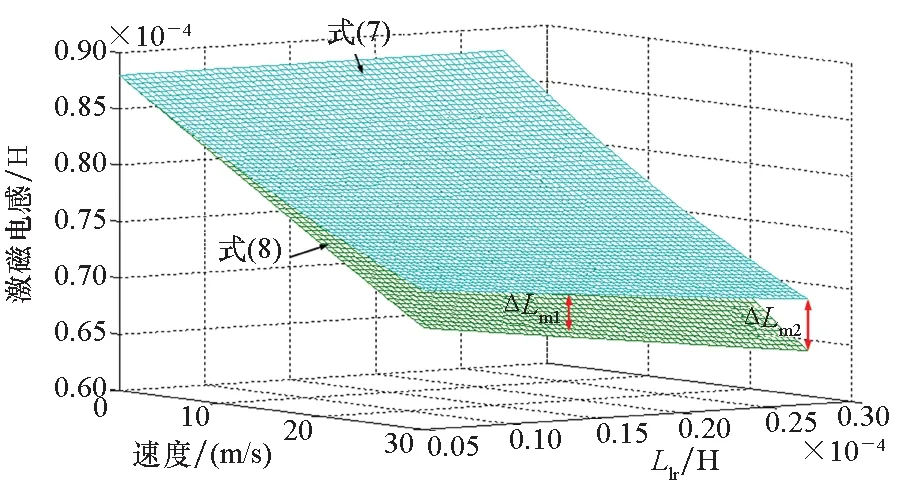
(a) 激磁电感随速度和次级漏感变化曲线(a) Variation of excitation inductance with speed and secondary leakage inductance

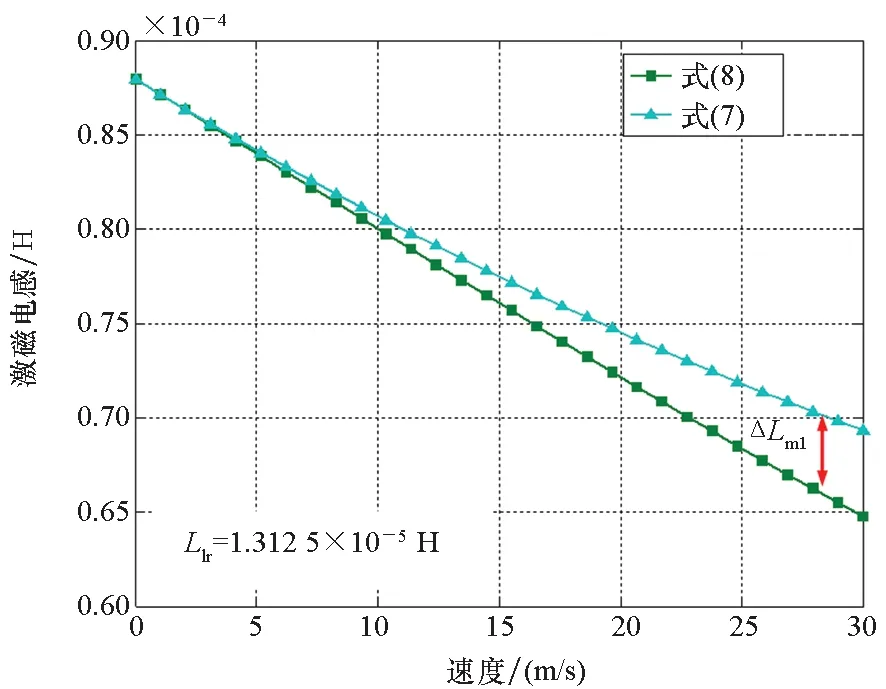
(b) 激磁电感随速度变化曲线(b) Variation of excitation inductance with speed

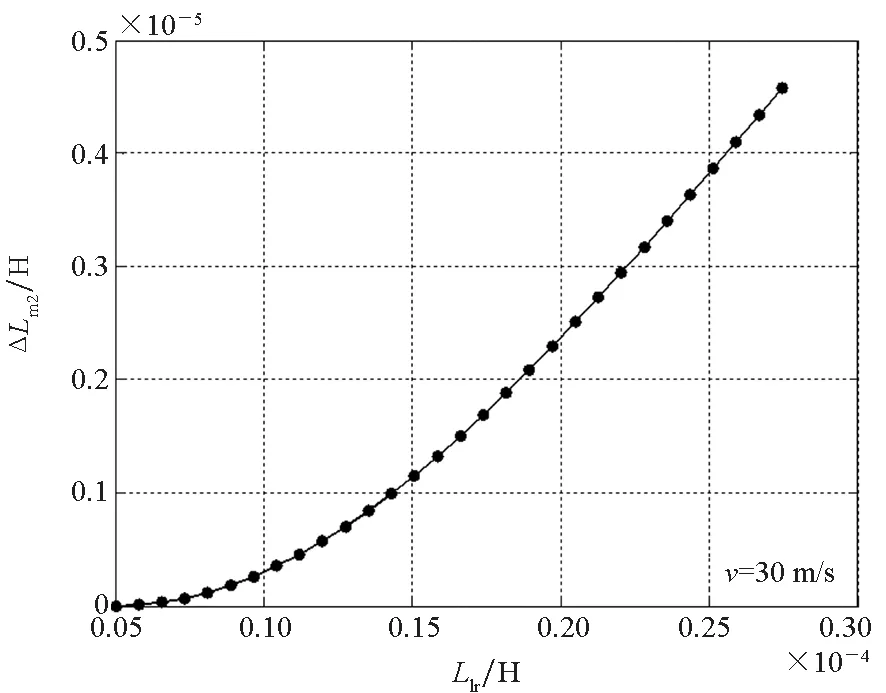
(c) 激磁电感差值随次级漏感变化曲线(c) Variation of difference value of excitation inductance with speed图4 激磁电感时变规律曲线Fig.4 Variation of excitation inductance

2 电机模型

直线感应电机动态运行时，初级在次级导电层上感应出的涡流会产生额外的损耗，该损耗主要由次级电阻消耗。根据式(1)得到感应涡流的有效值为：

(9)

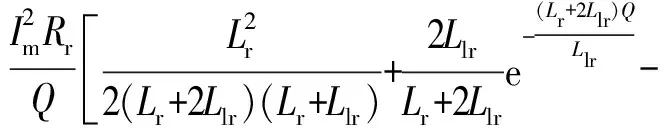
(10)

其中，k1为随速度时变的系数。如图1所示，动子运动时，其出端由于励磁磁通的消失，气隙中将会产生由导电层涡流感应出的磁通，因此在动子出端产生的损耗以磁能的形式体现，该损耗的表达式为：

(11)

其中，Emag为出端气隙磁场产生的磁能。将式(11)代入式(1)可求解得到：

(12)

其中，k2为随速度时变的系数。由动态边端效应造成的总损耗可表示为：

(13)

为了在等效电路中体现动态边端效应造成的损耗，需要在等效电路的励磁支路中增加一个损耗电阻，即Rloss=krRr。值得注意的是，此处的系数kr并非是次级电阻的修正系数，即等效电路次级支路上的电阻不含该系数。

根据本节的推导，可得到考虑动态边端效应时，动初级六相直线感应电机的等效电路如图5所示。

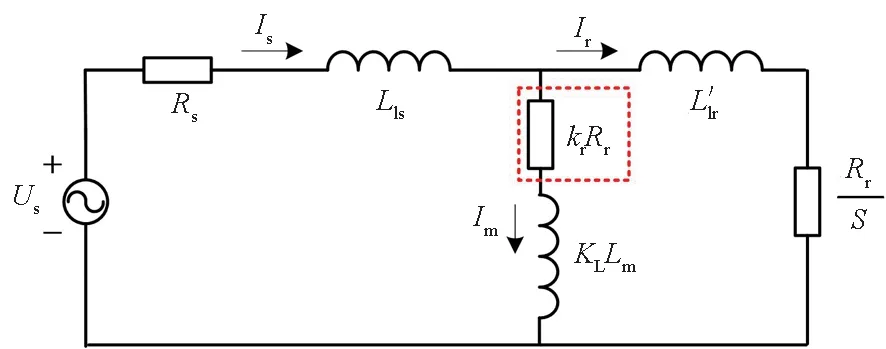
图5 动初级六相直线感应电机等效电路Fig.5 Equivalent circuit of short primary six-phase LIM

3 工作特性分析

3.1 推力特性

不考虑动态边端效应时，图5中激磁支路上没有框内的电阻，电机电磁推力的表达式为：

(14)

根据式(13)和图5可知，在考虑动态边端效应时，电机的功率等式为：

Ps=Pend_loss+Pm

(15)

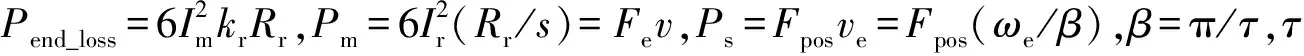
(16)

(17)

联立式(16)～(17)可得到，考虑动态边端效应后，电机的实际出力为：

(18)

利用上述推导结果，可对电机进行性能计算，并对计算结果进行对比分析。通过式(14)和式(18)可得到不考虑和考虑动态边端效应时，在恒定电流激励、恒定供电频率工况下，电磁推力与速度及滑差频率的关系曲线，如图6所示。

如图6(a)所示，由于动态边端效应的影响，随着速度的增加，推力逐渐下降，电机的最大出力随速度的增大而减小。图6(b)显示，在相同速度条件下，考虑动态边端效应时最大推力点对应的滑差频率(额定滑差频率)相比不考虑动态边端效应时有所增大。因此，在固定的供电频率下，额定滑差频率增大，转差率会增大，这解释了图6(a)中电机的最大出力随速度的增大而减小的原因。图6表明，由于动态边端效应的影响，电机最大出力及额定滑差频率随速度时变，因此电机的最大出力为相对值。

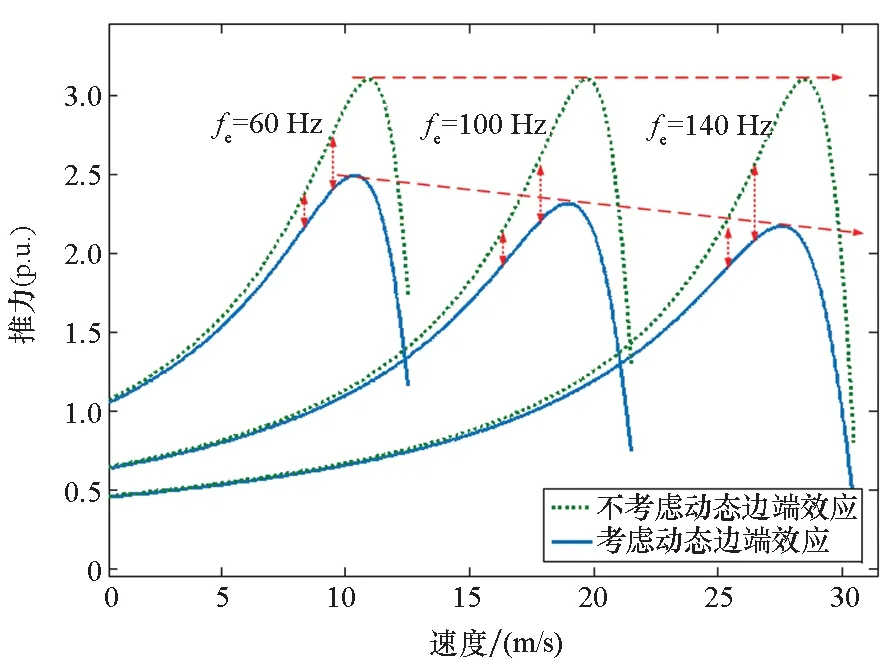
(a) 推力随速度变化曲线(a) Variation of thrust with speed

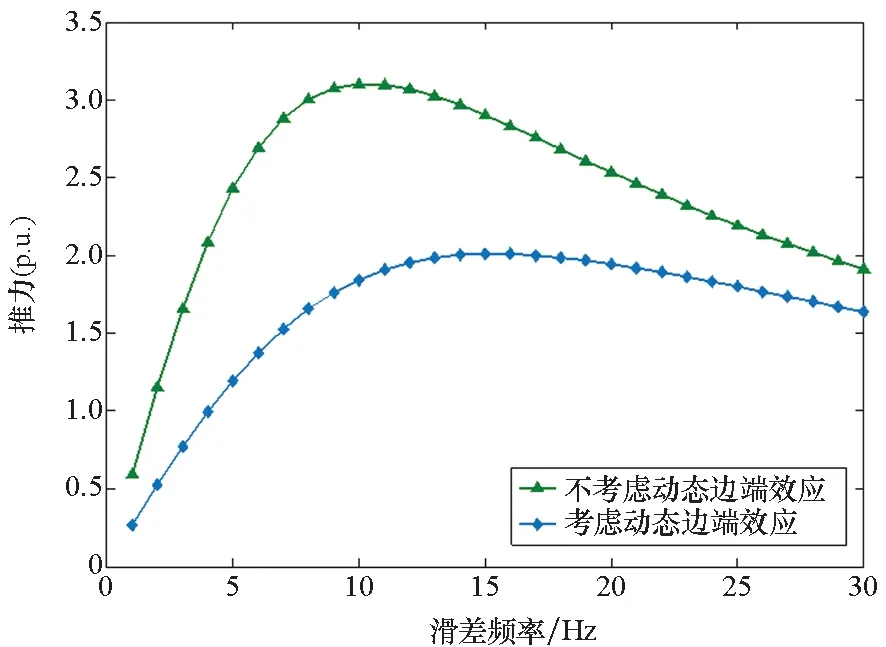
(b) 30 m/s下推力随滑差频率变化曲线(b) Variation of thrust with slip frequency under the speed condition of 30 m/s图6 推力随速度及滑差频率变化曲线Fig.6 Variation of thrust with speed and slip frequency

根据式(16)～(18)可分别计算出电机的正向推力、动态边端效应造成的反向推力以及电机的实际出力曲线，如图7所示。

(a) 电机正向出力及实际出力随速度变化曲线(a) Variation of forward, actual output thrust with speed

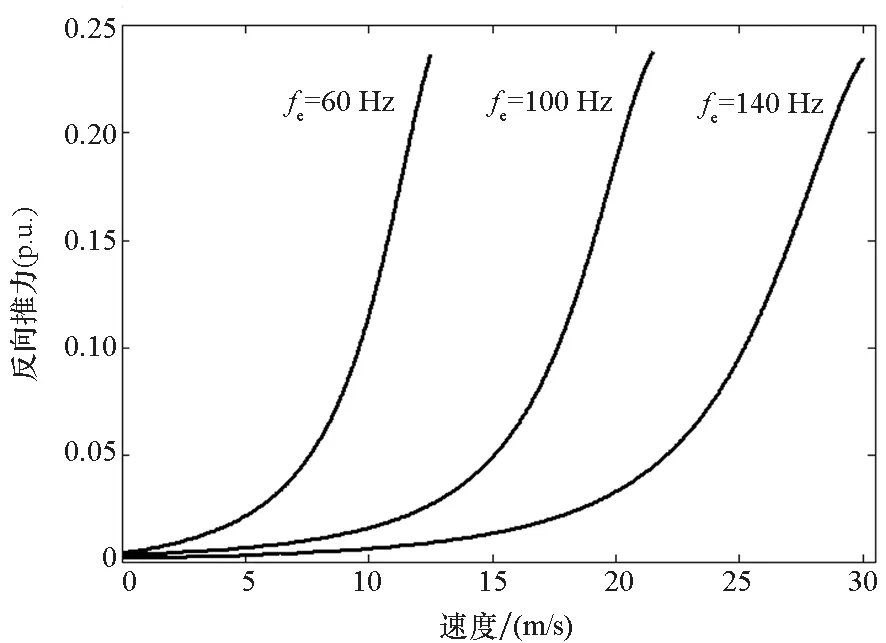
(b) 电机反向推力随速度变化曲线(b) Variation of reverse thrust with speed图7 考虑动态边端效应时电机正、反向推力及实际出力随速度变化曲线Fig.7 Variation of forward, reverse and actual output thrust with speed considering dynamic end effect

由图7 (a)可以看出，随着速度的增加，由于反向推力逐渐增大，导致实际输出推力不断下降。根据式(12)及图5可知，由于动态边端效应的影响，激磁支路中反映动态边端效应损耗的电阻随着速度的增大而增大，电机输入有功功率在该电阻上的消耗增大。部分文献认为激磁支路中的损耗电阻很小，可忽略，以简化电机模型。图7(b)表明，随着速度的增大，反向推力上升率明显增大，直观地反映了在高速区域，激磁支路的损耗电阻与次级电阻相比已不可忽视。因此，针对运行于高速工况的动初级直线感应电机，在建立数学模型时必须考虑动态边端效应造成的额外损耗。

利用文献[2，7]所提出的计算方法，建立麦克斯韦方程组，可得到一维电磁场推导得到的边端效应下电机的推力特性，将之与本节的推力计算结果进行对比分析，如图8所示。

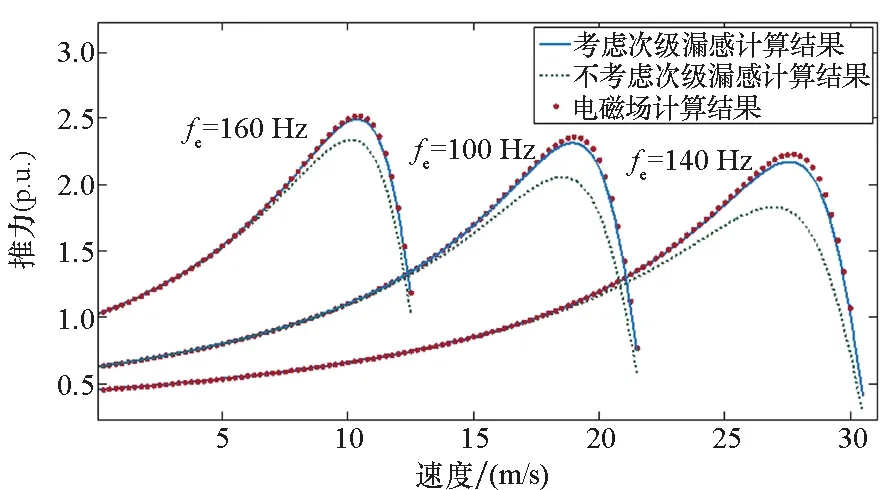
图8 不同方法计算推力结果对比Fig.8 Calculation comparison of thrust by different methods

由图8的对比可知，基于第1～2节推导结果计算得到的推力与电磁场计算结果更接近，而不考虑次级漏感的推力计算结果明显偏小。

3.2 效率评估

电机的效率是系统的重要指标。由于动态边端效应导致推力下降，并存在额外的涡流损耗，理论上电机的功率因数和效率会降低。根据图5电路方程可得到电机的功率因数及效率的表达式为：

(19)

(20)

将本文研究对象的初级参数(如表2所示)代入式(19)、式(20)得到恒定供电频率下功率因数和效率随速度的变化曲线如图9所示。

随着电机速度的增大，动态边端效应造成激磁电感衰减，涡流损耗增大，电机的有功需要克服边端效应。从图9可以看出，考虑动态边端效应时，功率因数和效率随速度的增大而减小，能够转化为有效电磁推力的功率在减小。有功不足时，电机的特性变软，推力下降，难以升速。由于动态边端效应的客观存在，除从电机结构上采取措施进行抑制外，通常需要基于准确的数学模型对推力控制策略进行改进和优化。

表2 电机初级参数

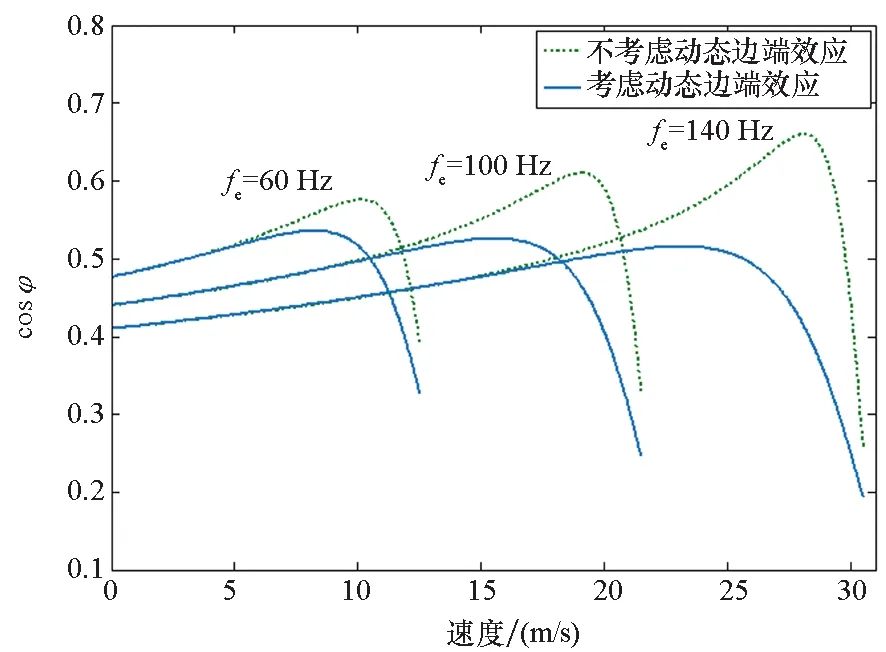
(a) 功率因数随速度变化曲线(a) Variation of power factor with speed

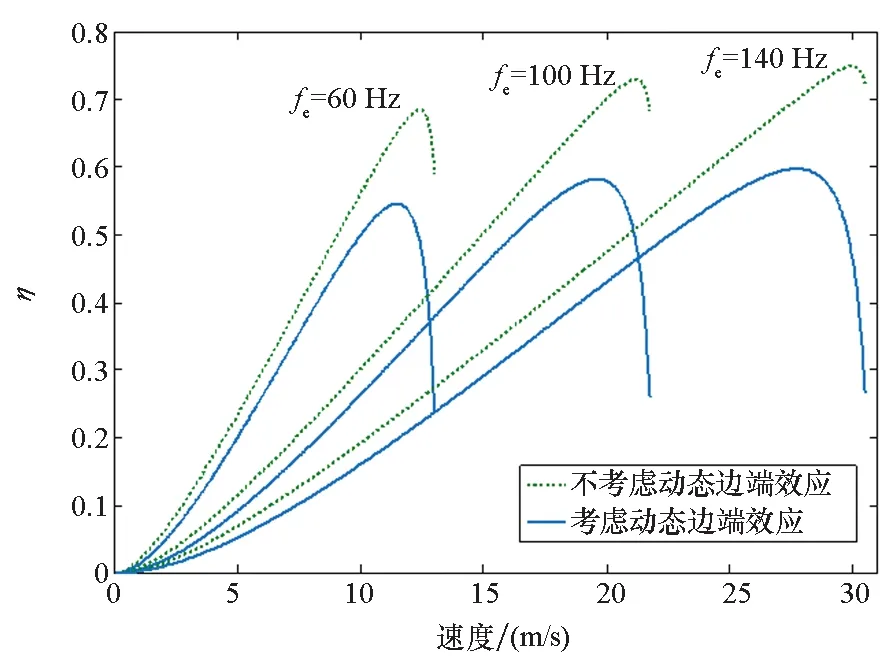
(b) 效率随速度变化曲线(b) Variation of efficiency with speed图9 功率因数及效率随速度变化曲线Fig.9 Variation of power factor and efficiency with speed

4 仿真及实验

4.1 有限元仿真验证

为了验证电机模型的准确性，采用有限元仿真进行验证。根据图6得到的结论可知，在动态边端效应的影响下，额定滑差频率随激磁电感的下降而增加。针对本文的研究对象，在实际控制过程中必须采用变滑差频率控制，使电机尽量靠近额定滑差频率点运行，以保证电机的出力最大。因此以一个固定的滑差频率来对比验证是不可取的。为了获取不同速度下的最大推力值，在Ansoft Maxwell中建立不同速度下有限元瞬态场模型，并进行不同频率条件下的仿真。在不同速度工况下，将有限元仿真得到的最大推力结果与理论计算结果进行对比，可验证分析方法和推导的正确性，如图10所示。

通过图10的对比可知，基于式(7)推力的计算结果更贴近于有限元仿真结果。因此基于式(7)所建立的数学模型能够基本准确刻画动态边端效应影响下电机的运行特性。

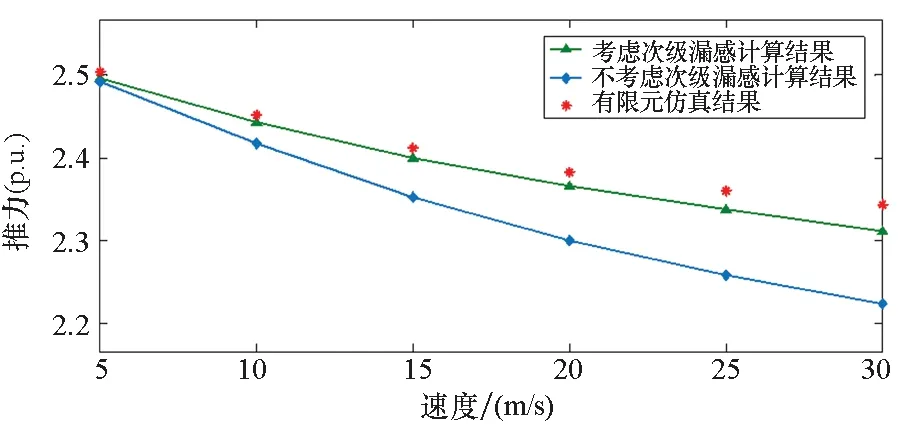
图10 有限元推力验证Fig.10 Thrust verification by finite element motor

4.2 实验验证

为了充分验证上述理论和仿真结果，搭建了大功率直线电机实验平台并进行了动态试验。试验平台如图11所示。通过充电机为储能单元充电。集中控制单元作为电机控制算法的执行者，调节逆变器输出电压以驱动直线电机。直线电机上安装有位置传感器，可观测动子的位置，进而计算出速度和加速度。集中控制单元将采集的位置、电流等数据用于闭环控制的反馈、状态监控以及上传给上位机，上位机可在每次实验之后通过MATLAB脚本解析每一次实验的数据。

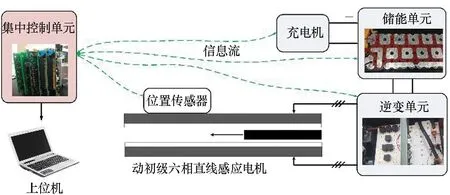
图11 实验平台示意图Fig.11 Schematic diagram of experimental platform

工作于非周期瞬态工况的直线感应电机的控制目标为动子带动负载在设定的目标位置达到目标速度，根据控制目标可生成参考加速度作为电机控制的输入。通过计算观测加速度误差(实际观测加速度与参考加速度的差值)可反映电机的推力跟踪效果，也就反映了矢量控制计算的准确性，进而验证电机模型的准确性。

设计一组实验，设定目标速度由10 m/s爬升至30 m/s，分别采用基于式(8)(方法一)和式(7)(方法二)的计算方法进行实验。实验结果如图12、图13所示。

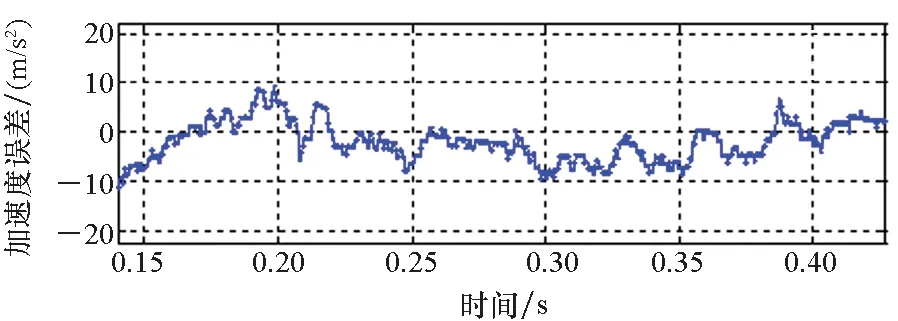
(a) v=10 m/s

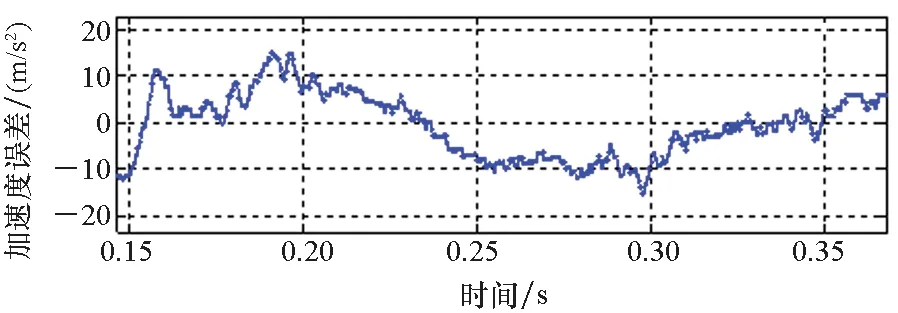
(b) v=15 m/s

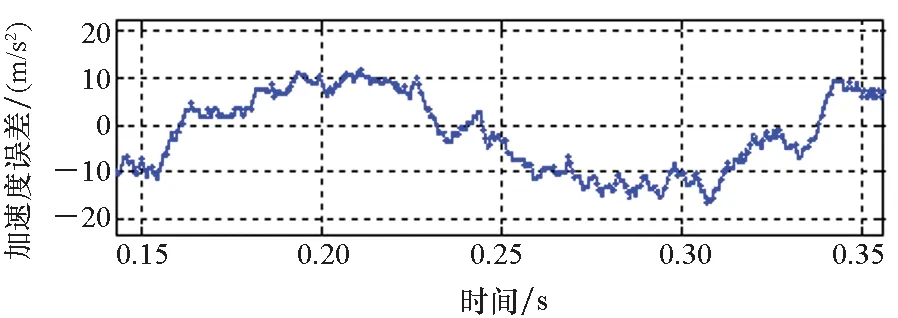
(c) v=20 m/s

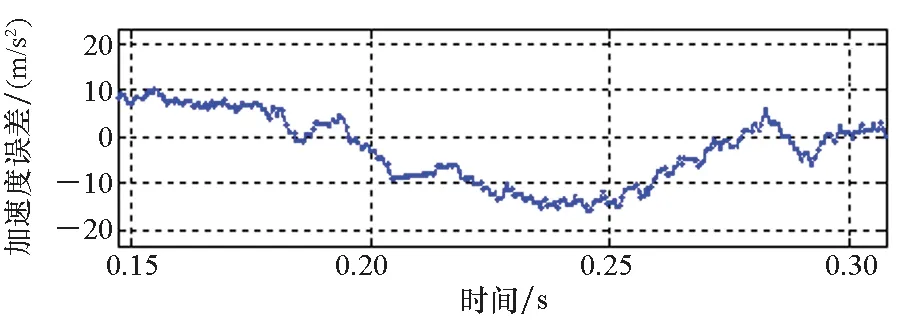
(d) v=25 m/s

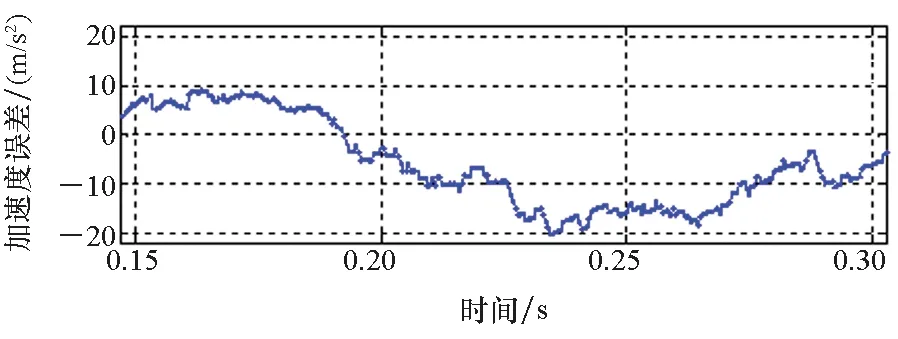
(e) v=30 m/s图12 采用方法一实验观测加速度误差Fig.12 Observed acceleration error by using method 1

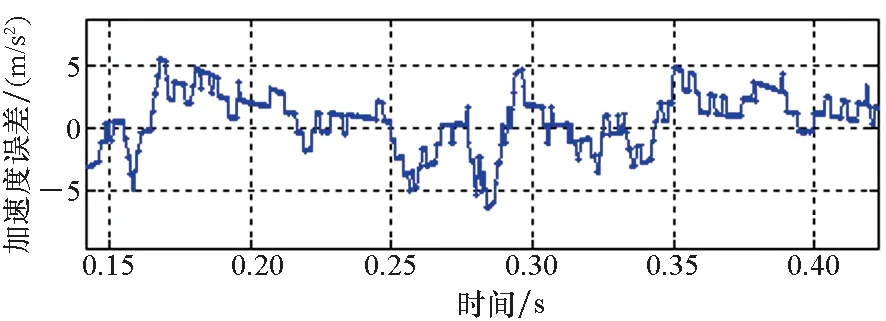
(a) v=10 m/s

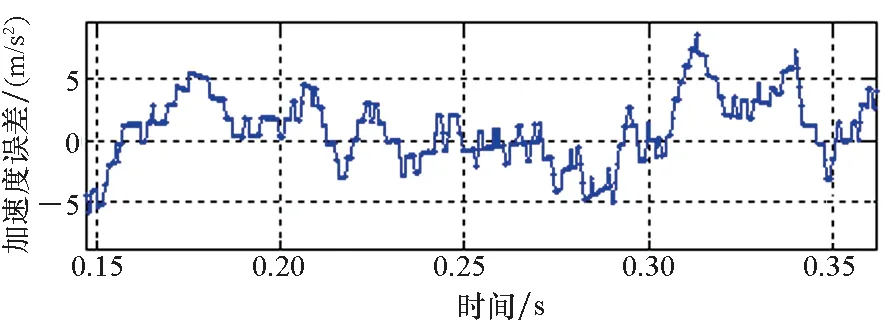
(b) v=15 m/s

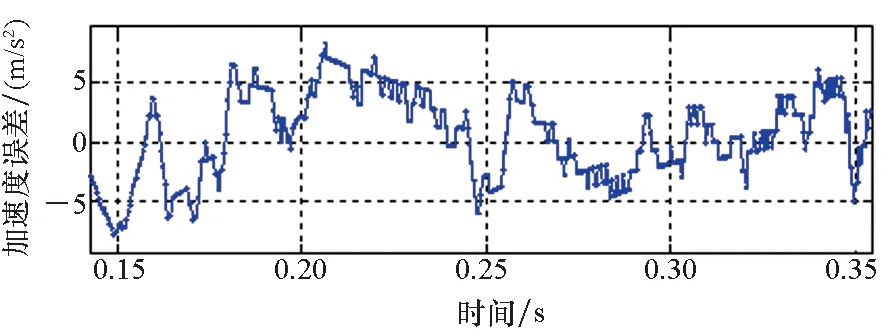
(c) v=20 m/s

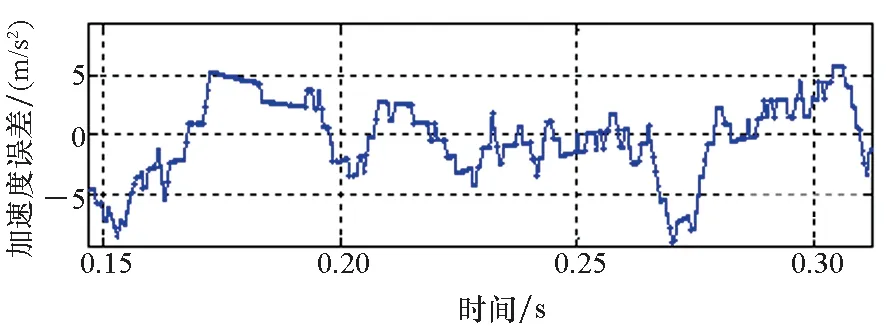
(d) v=25 m/s

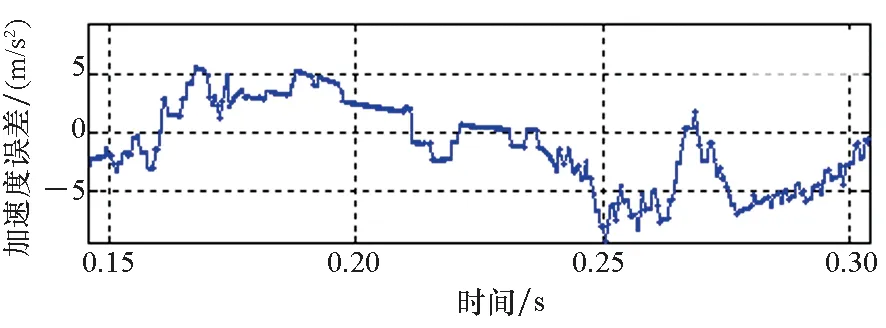
(e) v=30 m/s图13 采用方法二实验观测加速度误差Fig.13 Observed acceleration error by method 2

根据3.1节的分析可知，随着电机运行速度的爬升，动态边端效应带来的激磁电感下降及反向推力问题趋于严重。如图12所示，采用方法一进行实验，观测加速度存在明显的跌落，加速度误差随速度的增大而增大，最大误差达到近20 m/s2，与第3节分析得到的电机在动态边端效应影响下的运行特性相符。采用方法二进行实验，电机参数能够得到更准确的修正，则矢量控制中的有关推力、滑差频率、转矩电流的计算结果更准确。因此基于方法二进行实验能够有效减小加速度误差(均能控制在10 m/s2以内)，取得更好的推力控制效果，与第一节分析得到的结论一致。

5 结论

本文基于一阶等效电路瞬态涡流分析法推导了动态边端效应影响下动初级六相直线感应电机的参数时变规律。推导结果表明，次级漏感会阻碍感应涡流的瞬变，考虑次级漏感时激磁电感的下降率相比不考虑次级漏感更小，所刻画的电机模型更准确。通过电机的电磁方程推导对电机进行了性能计算与分析，指出动态边端效应会导致激磁电感衰减，涡流损耗增大，反向推力增大，有效输出推力下降，效率降低，这些特征随电机运行速度的增大而趋于明显。有限元仿真和动态实验结果表明，电机参数的时变规律和电机的工作特性与理论分析相符。