主动谐波消除多电平射频脉宽调制策略及其性能分析

陈剑斌，周 强，朱 蕾，张 江

(1. 陆军工程大学 通信工程学院, 江苏 南京 210007； 2. 国防科技大学 第六十三研究所, 江苏 南京 210007)

随着当前无线通信业务类型的快速增长，通信终端在小型化的同时需要兼容更多的功能和标准，从而在带宽、效率以及可重配置性等方面都面临更高的要求和挑战。传统模拟体制发信机中模拟射频器件参数固定，且效率、线性和带宽等主要性能指标在理论上相互制约[1]，从而极大制约了发信机的效率、体积以及可重配置等性能。软件定义无线电(Software Defined Radio，SDR)[2]采用数字信号处理技术完成传统模拟器件功能，可以实现对不同通信业务的适配，因此得到越来越多关注。其中，全数字发信机(All-Digital Transmitter，ADTx)[3]技术在数字域完成上变频和功率放大等射频功能，具有灵活的可重构和可编程性能，被认为是实现SDR系统的理想方案。

ADTx如图1所示，主要包含数字射频调制器、开关模式功放(Switched-Mode Power Amplifier，SMPA)以及调谐滤波器[4-6]，其中数字射频调制器完成基带信号的上变频和脉冲编码，生成脉冲序列以驱动后级SMPA实现高效放大。由于脉冲编码降低幅度分辨率，引入大量量化噪声，为保证输出信噪比和频谱纯度，需引入噪声整形技术，将带内量化噪声转换为带外噪声或谐波。因此基于噪声整形的脉冲编码算法不仅决定ADTx输出信号质量，而且直接影响后级SMPA工作效率，是ADTx实现高效率和高线性的核心。

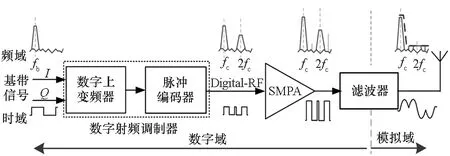
图1 ADTx系统框图Fig.1 Structure diagram of ADTx system

Delta-Sigma调制(Delta-Sigma Modulation，DSM)[7-8]和脉冲宽度调制(Pulse-Width Modulation，PWM)[9-11]是目前ADTx系统主要的脉冲编码技术。其中DSM能够实现更高的带内信噪比，但其硬件实现复杂度较高，且输出脉冲序列的切换频率数倍于载波频率，从而大大增加后级功放损耗[7]。同时，DSM输出脉冲序列在信号带外存在大量噪声，需要采用高Q值带通滤波器抑制，增加了系统实现难度。在传统PWM基础上，Raab提出射频脉宽调制(Radio Frequency Pulse Width Modulation，RF-PWM)技术[9]。相较于DSM，RF-PWM可以有效降低设计复杂度，且其输出脉冲序列切换频率仅为射频载波频率的2倍，可以有效减少功放损耗。此外，RF-PWM量化噪声体现为谐波分量，采用低通滤波即可实现信号恢复。因此，RF-PWM被认为是目前最适合ADTx的脉冲编码算法。

另一方面，在实际系统应用中，由于RF-PWM输出脉冲序列存在的大量谐波分量不仅影响编码效率，在宽频段应用下还对调谐滤波器设计提出较高挑战。通过增加输出脉冲序列电平数，多电平RF-PWM方案[12-14]在提升编码效率的同时，可在一定程度上降低谐波幅度，但仍需引入高Q值滤波器。为降低系统输出滤波要求，文献[15]提出将单个脉冲分解为多个窄脉冲的方案实现对谐波分量的抑制。但受采样频率以及实际硬件电路非理想特性制约，该方案仅适用于基带PWM。文献[16]提出了一种基于固定门限的多电平RF-PWM方案，实现对输出脉冲序列特定谐波的消除，但仅适用于恒包络信号。针对非恒包络信号，文献[17]提出了一种基于自适应门限与RF信号比较的多电平RF-PWM方案，实现非恒包络信号下特定谐波的主动消除。在文献[16-17]基础上，本文从谐波消除条件下各子脉冲序列的脉冲宽度要求出发，利用脉宽与信号幅度以及比较门限的关系，公式推导了基于3次谐波消除的5电平RF-PWM实现方案。同时根据方案中存在的基波分量与信号幅度间的增益变量，分析验证了谐波抑制条件下的最佳增益系数。

1 固定门限比较RF-PWM

传统的RF-PWM方案[9]通过将已调射频信号与特定参考信号进行比较，得到一个与载波同频且幅度固定而脉冲宽度可变的脉冲序列，其中原始调制射频信号的幅度和相位信息分别对应于RF-PWM脉冲的宽度和延时。由于该方案采用变化的比较参考电压，在高采样率条件下硬件实现难度较高。为降低开关频率且易于实现，可通过对输入已调射频信号进行预处理后再与固定的门限电平进行比较以产生最终的RF-PWM信号[11]。

固定门限比较RF-PWM输出脉冲波形的情况如图2所示。考虑输入为归一化的已调射频信号Sin(t)=a(t)cos(2πfct+φ(t))，a(t)和φ(t)分别为归一化的包络和相位信号，且有0≤a(t)≤1。则脉冲序列SPWM(t)可通过Sin(t)和比较门限电平Vth及-Vth的交点来定义。

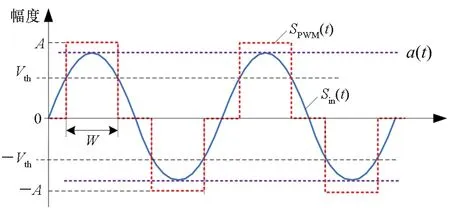
图2 固定门限比较RF-PWM输出脉冲波形产生示意图Fig.2 Sketch map of RF-PWM pulses with fixed-comparison-threshold

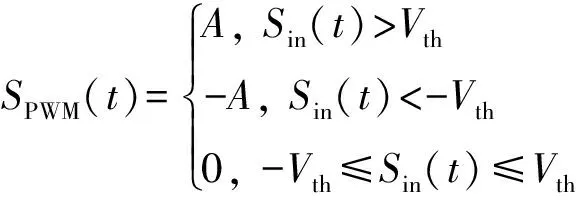
(1)

其中，A为调制器输出幅度，为便于分析后文令A=1。假设满足载波频率远大于包络信号的a(t)带宽，则在一定射频周期内a(t)可近似为恒定值，对应周期内Sin(t)可看作正弦信号。利用部分傅里叶级数分析方法[18]，SPWM(t)可表示为：

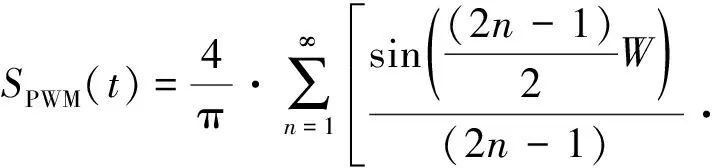
(2)

其中，ωc=2πfc，n为正整数，W为脉冲宽度。

(3)

考虑到SPWM(t)具有半波对称性，仅含奇次谐波，则由式(2)可得对应的第n次谐波幅值An。

(4)

根据式(3)和式(4)可得SPWM(t)的基波分量幅度为：

(5)

式(5)同时也是非恒包络信号下固定门限比较RF-PWM的AM-AM传递函数。为保证RF-PWM最终实现线性输出，A1与a(t)需为正比关系。基于此，固定门限电平比较策略在保持门限Vth固定的同时引入预失真技术对基带信号幅度a(t)进行预处理。定义预处理后的幅度为：

(6)

由式(5)～(6)可知，此时A1= 4A/π·a(t)，其中4A/π为调制器增益。由于a(t)不能为1，因此a(t)的动态范围将受限，推荐其最大值在0.9～0.95范围内[11]。

为提升脉冲编码性能，可以通过增加比较门限数量以提升输出脉冲电平，对应M电平脉冲序列SML-PWM(t)的第n次谐波幅值An_ML为：

(7)

其中，K=(M-1)/2。则M电平RF-PWM的AM-AM传递函数为：

(8)

K>1时，式(8)的反函数难以获得解析表达式，此时可通过软件预先计算后采用存储查表的方式获取用于幅度校正的预失真幅度值。

2 主动谐波消除RF-PWM策略

2.1 策略基本原理

已有固定门限多电平RF-PWM方案通过引入多个比较门限并对a(t)进行式(8)所示的预失真校正，可以确保多个子脉冲波形的基波分量之和A1_ML与a(t)成正比。通过进一步增加量化电平，可以一定程度实现RF-PWM输出脉冲序列高次谐波分量抑制，但抑制效果有限[16]。注意到式(7)所示的脉冲宽度与谐波幅度的关系，考虑通过控制各个子脉冲的宽度，以实现对特定谐波分量的主动消除。

假设需要消除L个不同次的谐波分量，如X1次、…、Xj次、…、XL次，其中L为正整数且1≤j≤L。根据K个子脉冲基波分量叠加之和正比于a(t)，以及L个奇次谐波分量加权之和为零的思路，可得到K个自适应门限的解析公式。基于上述方法，利用K个自适应门限最多可实现K-1个奇次谐波的主动消除[17]。另一方面，为降低输出滤波的要求，应优先选择消除离载频最近的谐波。因此，下文将以3次谐波消除为例，给出对应RF-PWM的具体实现方案。

2.2 次谐波消除RF-PWM实现方案

根据前面的分析，要实现3次谐波消除，至少需要2个自适应门限。另一方面，增加门限数量会使对应解析计算变得困难，同时RF-PWM输出电平数量增加也提升了后级SMPA电路实现的复杂度。因此，下面分析采用2个自适应门限来实现3次谐波抑制，此时对应两个3电平子脉冲序列组合生成5电平PWM，如图3所示。其中，Vth2≥Vth1。则根据前面的分析有：

(9)

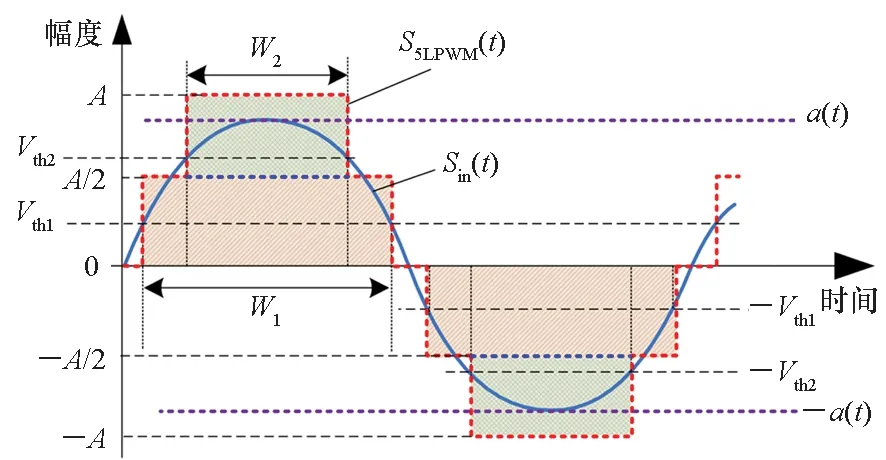
图3 5电平RF-PWM波形产生示意图Fig.3 Sketch map of 5-level RF-PWM

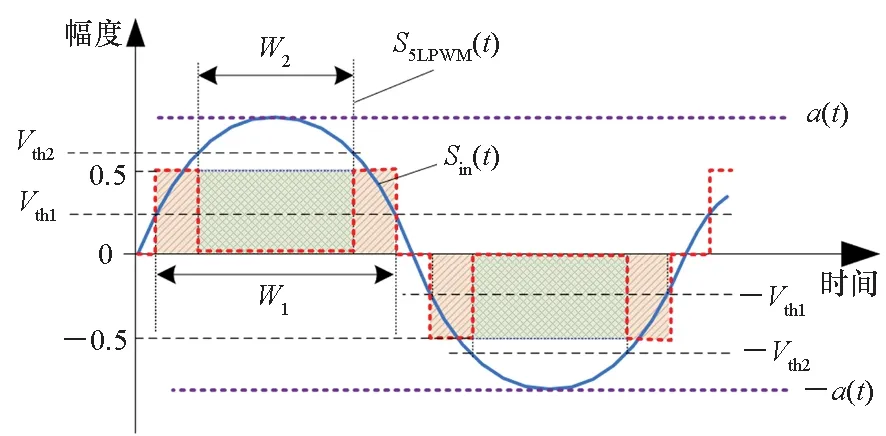
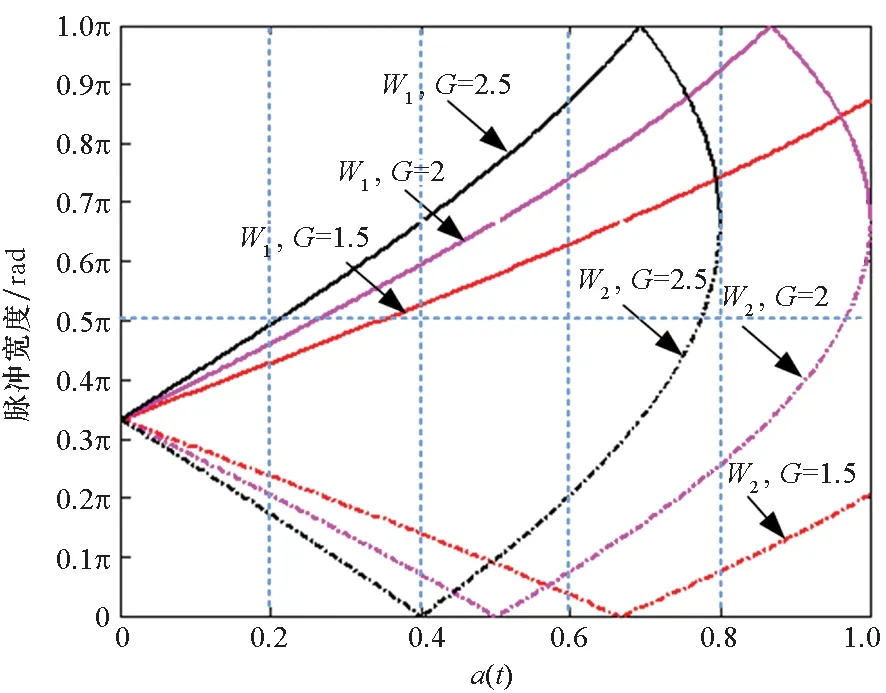
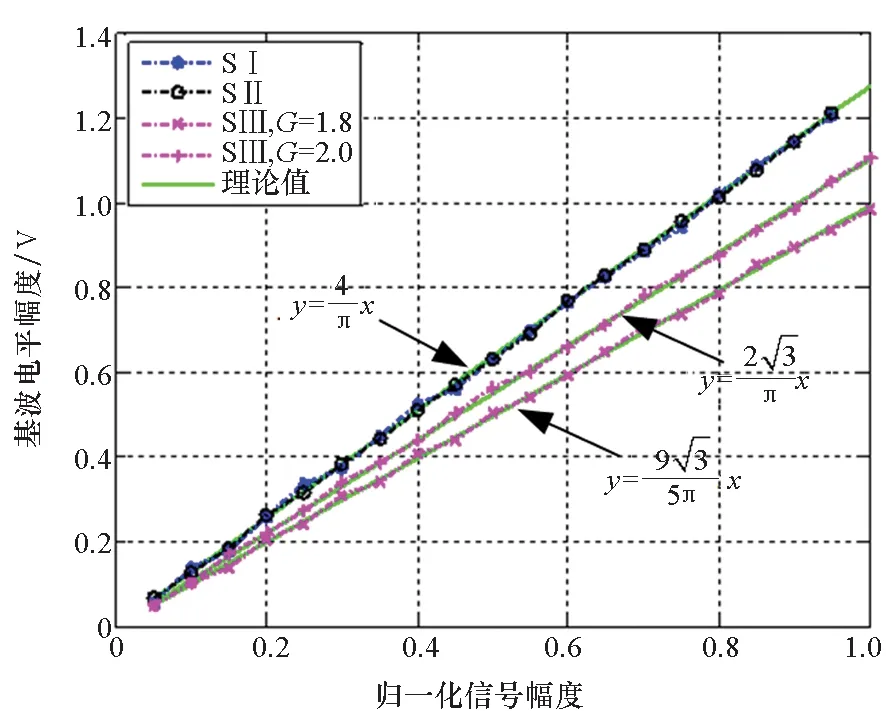
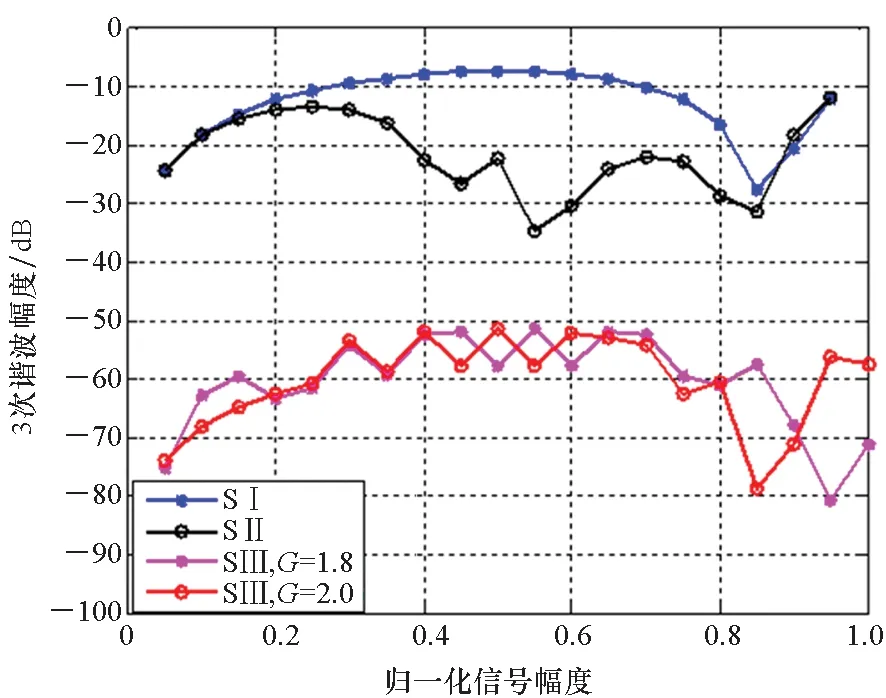
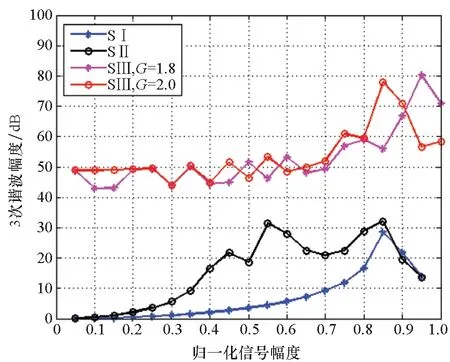
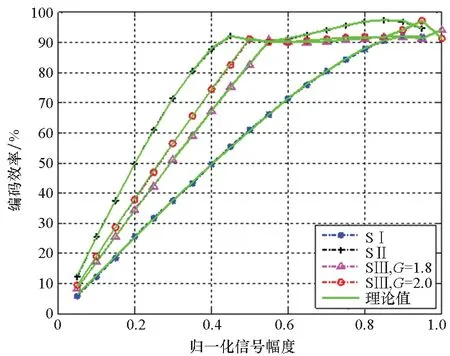
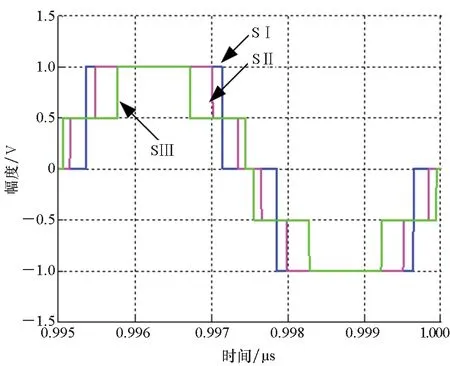
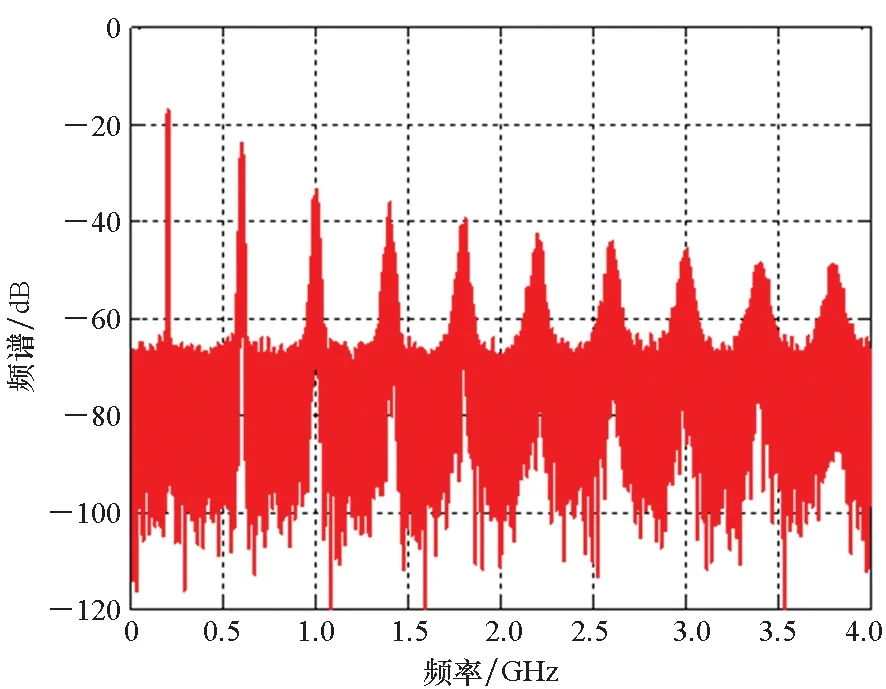
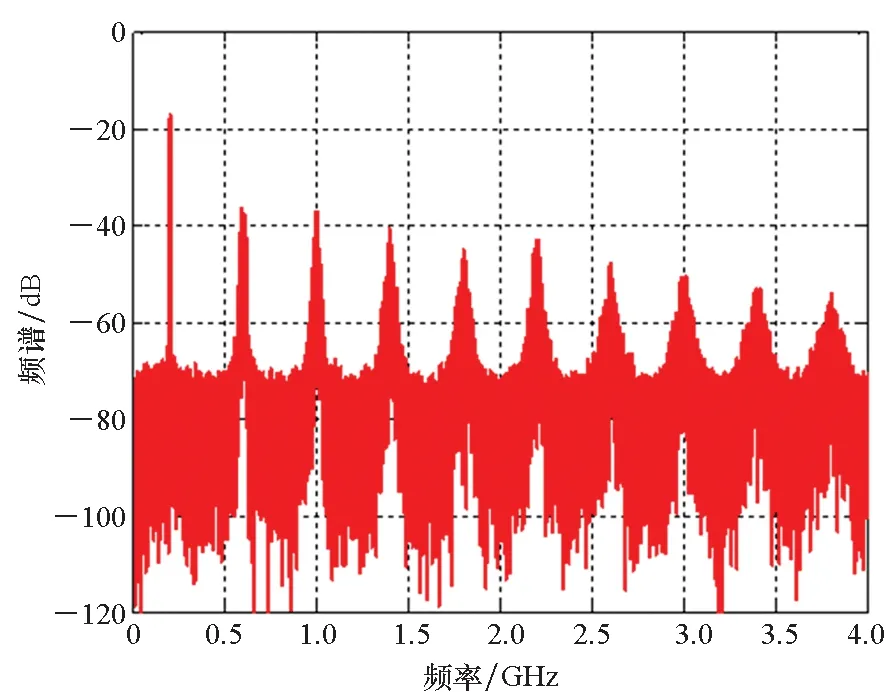
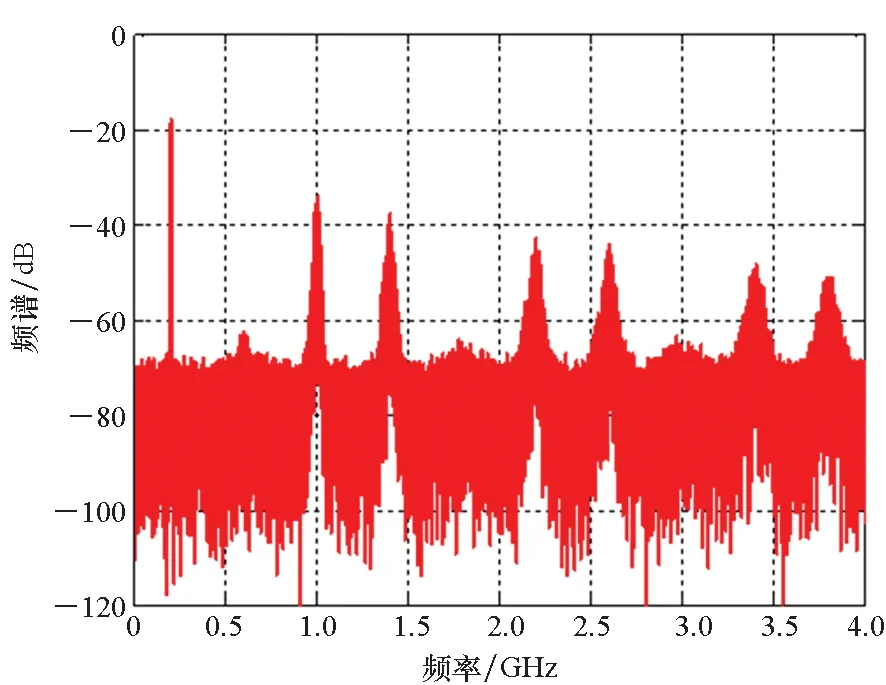
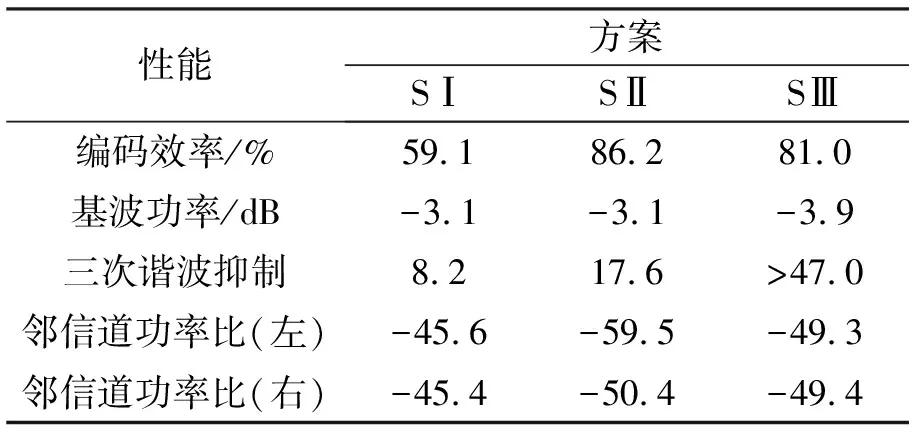
为确保策略的硬件可实现性，调制器增益g有限定的取值范围，且具体取值与策略调制性能直接相关，下文将进行具体说明。另外，考虑到0

W1+W2=0

(10)

或

(11)

或

(12)

对于W1+W2=0，此时A1_5L=A3_5L=0，不满足3次谐波消除RF-PWM策略的设计要求。当W1+W2≠0，将式(10)～(12)代入式(9)，可以得到基波幅度为：

(13)

进一步根据式(3)中门限与脉宽之间的关系可得：

(14)

进一步根据式(3)还可得：

(15)

另一方面，根据上述推导过程中脉冲宽度W1和W2各自的取值范围以及两者之间需满足的限定关系，可以得到1/G≤a(t)≤2/G。当a(t)<1/G时，联立式(10)～(11)对应的方程无解，说明此时满足3次谐波消除条件的2个子脉冲波形之和的基波分量无法与输入信号幅度保持正比关系。为解决这一问题，当a(t)<1/G时，采用2个子脉冲波形差来实现对3次谐波的消除，同时保证对应的基波幅度与a(t)的线性关系，如图4所示。

图4 5电平RF-PWM波形产生示意图(a(t)<1/G)Fig.4 Sketch map of 5-level RF-PWM(a(t)<1/G)

此时为实现3次谐波消除，脉冲宽度应满足：

(16)

对应基波幅度为：

(17)

根据门限与脉宽之间的关系，最终可以得到：

(18)

(19)

根据当前输入采样时刻RF信号的输入幅度，生成如式(18)～(19)所示的比较门限，并按式(1)执行比较操作，即可生成3次谐波抑制的5电平RF-PWM序列。此外，考虑到正余弦函数的周期性，若sinθ=0或cosθ=0，且x为奇数(输出脉冲仅含奇次谐波)，则对应有sin(xθ)=0或cos(xθ)=0，因此根据式(9)，容易验证所提方案还可以消除特定次谐波的所有奇数倍谐波。

3 谐波消除RF-PWM性能分析

3.1 理论分析

根据2.2节分析可知，主动谐波抑制方案应首先保证12-3G2a(t)2≥0。为使上述条件在所有幅度取值范围内成立，可得增益系数的取值范围为0

为进一步理解上述范围的含义，基于式(18)～(19)，利用式(3)可以得到对应的两个子脉冲宽度W1和W2与输入信号幅度之间的关系：

(20)

(21)

增益系数分别为1.5，2.0，2.5时对应的关系曲线如图5所示。从图5中可以看出，当增益系数为2.5时，幅度a(t)>2/G=0.8时，对应脉冲宽度W1和W2无实数解。说明在此范围内，满足谐波抑制条件的RF-PWM脉冲序列基波幅度与信号幅度无法满足线性关系，从而实际发送信号中将引入失真，且G越大，对应失真也越大。另一方面，注意到G=2时，恰好保证在幅度a(t)的全部取值范围内都存在实数解。综上所述，G≤2是3次谐波消除5电平RF-PWM实现的必要条件。下面进一步分析主动谐波抑制策略的调制性能。

图5 不同增益系数下脉冲宽度与信号幅度的关系Fig.5 Correlation of pulse-width and amplitude for different gain index

除了谐波抑制，考虑到实际系统中存在的电路寄生电容会增大输出脉冲的上升、下降延时，当包络幅度较小即脉冲较窄时，将引起脉冲畸变甚至丢失，从而引入额外失真。因此最小脉冲宽度也是脉冲编码算法需要关注的指标。首先根据图5中子脉冲宽度W1和W2与输入信号幅度a(t)之间的关系曲线，同时注意到当a(t)<1/G时最小子脉冲宽度为W1-W2，容易得到：增益系数G越小，对应的主动谐波抑制RF-PWM序列最小脉冲宽度也越小。因此从增大最小脉冲宽度的角度出发，最佳增益系数值应取2。

在最佳增益系数值下进一步分析主动谐波抑制RF-PWM方案与现有固定门限方案之间的最小脉冲宽度情况。根据不同方案下比较门限与输入信号幅度的具体关系，进一步利用式(3)可以得到不同RF-PWM方案下的最小门限与输入信号幅度关系，对应结果如图6所示。其中，固定门限5电平RF-PWM预失真信号幅度由查表方式得到，对应的两个比较门限电平分别为0.1和0.35。可以看到，相比现有固定门限RF-PWM，主动谐波抑制RF-PWM使得序列最小脉冲宽度减小，从而一定程度上加剧了信号失真。实际应用中为消除脉冲宽度压缩的影响，可以引入相应的预失真方案来实现脉冲畸变的补偿[19]。

图6 最小脉冲宽度与输入信号幅度理论关系曲线Fig.6 Theoretical curve for correlation of minimum-pulse-width and input-amplitude

另一方面，脉冲编码算法的另一个重要指标是编码效率，该指标直接影响ADTx系统的整体效率。编码效率定义为实际发送RF信号功率PS与脉冲编码序列功率PA之比[12]。

(22)

下面具体分析不同RF-PWM方案的编码效率性能。对于现有固定门限电平方案，3电平下脉冲序列编码效率为：

(23)

k为固定常数，代表仿真中基波电平到实际基波功率的变换系数。由于5电平下对应的子脉冲幅度宽度无法得到对应解析表达式，因此后文将结合仿真分析其编码效率性能。另一方面，对于主动谐波抑制RF-PWM脉冲序列，根据不同幅度下子脉冲具体组合方式的不同，可以得到序列功率：

(24)

3.2 性能仿真验证

结合理论分析，利用MATLAB软件仿真验证分析主动谐波抑制RF-PWM的性能。为进行对比，同时仿真固定比较门限RF-PWM策略。其中固定门限3电平为方案SⅠ，采用比较门限0.1。基于固定比较门限5电平RF-PWM为方案SⅡ，采用比较门限0.1和0.3。主动谐波抑制RF-PWM为方案SⅢ，并在仿真中分别令G=1.8/2.0，以验证增益系数G对策略性能的影响。根据前面分析，具体仿真时，固定门限策略RF-PWM根据输入信号幅度，先进行幅度预失真再执行比较操作，主动谐波抑制RF-PWM则是根据当前时刻幅度先确定两个比较门限值，再执行比较。

(a) 基波幅度(a) Amplitude of based harmonic

(b) 3次谐波功率(b) Power of 3rd harmonic

(c) 3次谐波抑制 (c) 3rd harmonic suppression

(d) 编码效率(d) Coding efficiency图7 单音输入功率回退下的RF-PWM性能Fig.7 Performance of RF-PWM for back-off signal-tone input

图7(b)、(c)给出了3次谐波抑制情况。通过增加量化电平，SⅡ相比于SⅠ，其3次谐波抑制性能有所提升，但提升仅限在一定输入信号幅度范围内(0.25≤a(t)≤0.85)。对于SⅢ方案，其3次谐波抑制能力在全范围内显著优于SⅠ和SⅡ，即使相比SⅡ也能够获得25～50 dB的性能提升，从而验证了本文方案的有效性。同时注意到，不同增益系数下，3次谐波抑制性能基本相同。这主要是由于时域仿真分辨率受限，无法精确实现谐波抑制所需的理论脉冲宽度。

进一步对比各方案的编码效率，如图7(d)所示，图7(d)中同时给出了相应的理论曲线。可以看到，理论值和仿真值基本吻合，同时得益于量化电平的增加，SⅡ和SⅢ的编码效率均优于SⅠ。进一步对比SⅡ，虽然SⅢ输出脉冲序列的总功率要小于SⅡ，但由于此时调制器增益和输出脉冲基波功率的降低，其编码效率反而要小于SⅡ。尤其是当信号幅度a(t)<1/G时，此时SⅢ退化为3电平，与SⅡ的序列功率差值减小，而两者调制器增益差值恒定，使得此时编码效率出现较大差距。此外，随着增益系数G的降低，基波功率减小，对应SⅢ编码效率性能下降。这进一步验证了增益系数G的最佳值。

在非恒包络复杂调制信号下对比不同方案的调制性能。采用峰均功率比(Peak to Average Power Ratio, PAPR)为6.35 dB，载波频率为200 MHz，符号速率为5 Mbit/s的16 QAM信号作为RF-PWM的输入信号，信号等效采样频率为20 GHz，SⅢ方案采用最优增益系数G=2.0。图8分别给出了方案SⅠ，SⅡ和SⅢ下的脉冲序列时域波形及其对应的输出频谱。可以看到，在相同的输入信号和仿真条件下，方案SⅠ下得到的调制信号具有最大的各次谐波。对于方案SⅡ，其各次谐波皆小于SⅠ。而SⅢ的3、9次等3x次谐波已基本被消除(与底噪基本平齐)，因此离射频信号最近的谐波为5次谐波。

(a) 时域波形(a) Time domain wave

(b) SⅠ方案(b) Method of SⅠ

(c) SⅡ方案(c) Method of SⅡ

(d) SⅢ方案(d) Method of SⅢ图8 16QAM输入下不同方案的输出特性Fig.8 Output feature for different pulse-coding methods with 16QAM input

表1给出了在相同输入信号和仿真条件下，三种RF-PWM方案的性能对比。可以看出，SⅡ和SⅢ的主要性能指标，如编码效率、谐波抑制、邻信道功率比等，几乎全面优于SⅠ。进一步对比两种5电平方案，可以看到SⅢ的大部分指标和SⅡ相当，虽然在编码效率等指标上略差于SⅡ，但SⅢ在谐波抑制上的明显优势将对滤波器的设计和实现提供有力支撑，从而有利于提高ADTx的综合性能。

表1 16QAM信号输入下不同脉冲编码方案的性能对比Tab.1 Performance comparison for different pulse-coding methods with 16QAM input

4 结论

通过对多个子脉冲序列的脉冲宽度进行控制，在确保子脉冲基波分量加权和与输入RF调制信号幅度保持正比关系的同时，可以实现对特定谐波的消除。同时通过优先消除低次谐波，主动谐波抑制RF-PWM策略能够有效降低ADTx系统对后级成型滤波器的设计要求，有利于提升宽频段整体性能。

基于上述思想，以3x次谐波的主动消除为例，本文根据脉冲宽度与输入信号幅度、比较门限之间的关系，推导了5电平RF-PWM的具体实现方案。在此基础上，针对信号幅度与基波幅度的增益变量，分析了增益系数对谐波抑制方案的性能影响及其最优值，并通过性能仿真在验证理论分析结果的同时证明了主动谐波消除RF-PWM策略的有效性。