氯盐侵蚀下开裂混凝土耐久性可靠度研究

兰瑞鑫， 李 扬， 叶梦琦

((湖北工业大学土木建筑与环境学院， 湖北 武汉 430068)

在当今社会的快速发展过程中，建筑结构材料的运用越来越受到重视，由于混凝土具有资源丰富、制作简单的特点，使它成为运用最为广泛的建筑结构材料[1]。由于混凝土运用的广泛程度，混凝土的耐久性开始慢慢被人重视起来。

对于混凝土耐久性的探讨中，混凝土结构失效最大的原因之一是氯离子侵蚀，因为其会加速钢筋的锈蚀，对于现有氯离子的传输方式，大部分是基于现有的数学模型与试验[2-4]。对于已有的试验现象以及结论，大部分学者已经总结出了氯离子扩散系数与各个因素如温度、时间之间的关系，并依次给出了它们的计算模型[5-7]。与此同时，目前普遍研究认为混凝土开裂会加剧氯离子的入侵，通过控制裂缝宽度来延缓氯离子入侵，延长结构的设计使用寿命。据此有学者开展了大量带裂缝混凝土耐久性相关研究[8-10]。同时已经有研究者注意到混凝土裂缝控制对耐久性影响具有一定模糊性[11]，然而如何将这种模糊性影响用更加合理的方式体现在耐久性评估和应用中，尚需深入研究。因此在时间、温度、相对湿度的基础上对氯离子扩散的计算模型进行修正，并对其进行可靠度分析。

本文的相关结论与数据可以为沿海地区的建筑结构防护措施提供相关的思路,并对它们的使用寿命提供参考。

1 带裂缝混凝土结构氯离子侵蚀试验研究

1.1 计算模型的修正

对于完整混凝土内部氯离子传输方式的计算模型，涉及到很多的因素影响，较为复杂，因此为了方便计算并且结合了大量学者的实验与结论，得出时间、温度、湿度这三个因素对氯离子的传输方式有较大影响，因此参考以往学者的计算模型，对于这三个影响条件，在原有的计算模型的基础上进行修正

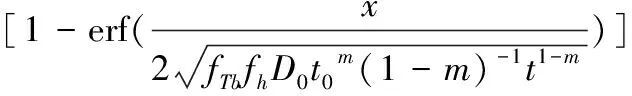
(1)

式中，C0是氯离子最开始的浓度，Cs是氯离子接近钢筋时的浓度，D0是扩散的系数，m是混凝土性能的关于时间的一个指数，erf(·)为高斯误差函数，fTb与fh是各自与温度、湿度相关的修正系数。

在以往的试验过程中，大量研究人员都是基于双重孔隙模型[12]来对此问题进行描述与探讨。对于饱和状态下的扩散规律可以采用Fick第二扩散定律来描述这个过程，因此，考虑以时间、温度、湿度以及裂缝为影响条件，对算式模型进行修正，得到如下算式

(2)

式中，f(w)为裂纹效应函数，其他符号意思与公式(1)相同。

裂纹效应函数不能直接得出，因此为了更好的对这个扩散模型进行计算，需要开展饱和状态和非饱和状态下带裂缝混凝土的耐久性试验研究，以期获得f(w)的修正表达式。

1.2 试验条件

设计混凝土试件共18块，试件尺寸为300 mm×100 mm×100 mm的立方体试块。混凝土试块的配合比如表1所示。

表1 配合比设计

该实验进行对比实验，实验设置A、B两组混凝土试件模拟处于不同条件下的氯离子侵蚀环境，其中A组模拟全浸泡区环境，B组模拟干湿循环区环境，两组分别设置9组试件，每组的实际裂缝宽度详见表2。试验的详细设计情况与具体编号见表2。

表2 设计方案

实验按照预先计算好的配合比对混凝土进行拌制，然后将其注入模具中，模具的大小为300 mm×100 mm×100 mm，在对混凝土进行浇筑之前预制裂缝，预制裂缝时选用厚度分别为0.25 mm、0.5 mm、0.75 mm和1 mm的4个不同尺寸的小钢片。但混凝土本身在浇筑时受人为影响以及自身的流动性，钢片会发生偏移，造成裂缝宽度的不精确性，因此采取保护措施。将钢丝横过试件上方，并在两方使用木板压住，随后再将夹了钢片的夹子固定于钢丝上，保持树立，插入深度为25 mm。并把不同厚度钢片对应的模具分组标上序号，再将拌制好的混凝土依次灌注进不同标号的模具中，具体试验操作步骤如图1所示。

图 1 浇筑试块

待浇筑完成2 h后，依次拔出钢片，放置24 h后把得到的预制裂缝构件放入标准养护室养护28 d。养护时间结束后取出构件并对其进行干燥处理，为期2 d。等到干燥处理结束之后，将试件放入浓度为5%的NaCl中，具体浸泡过程如图2所示。

图 2 浸泡试验

待浸泡试验完成后，将试件全部拿出并等待48 h，观察等到试件全部自然干燥后对试件进行取粉工作，随后利用RCT法[13-15]测量试件中的氯离子含量。分别制备三种不同浓度的NaCl溶液对待测溶液标定，溶液浓度分别为5×10-3Mol/L，5×10-4Mol/L，5×10-5Mol/L，标定完毕后依次检测溶液中的氯离子含量。

1.3试验结果

试验完成后，对于A、B两组实验测得的实际数据进行曲线拟合，将氯离子含量数值进行线性拟合、多项式拟合以及指数拟合。计算结果见表3和表4。

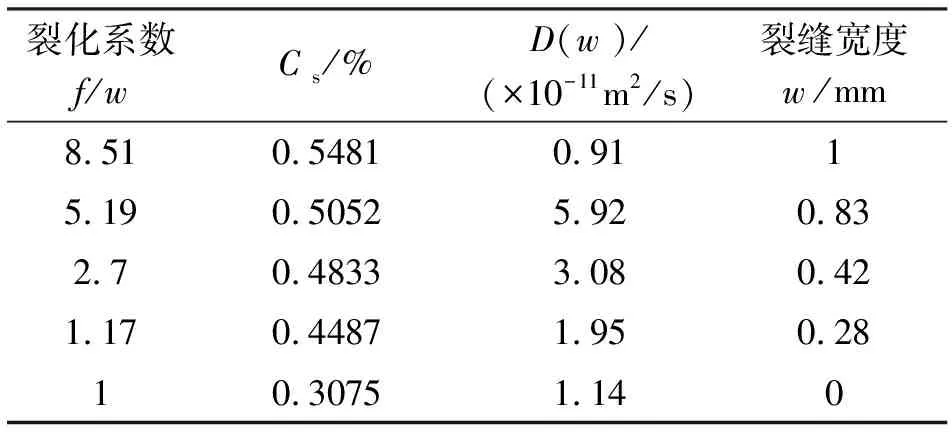
表3 饱和状态下

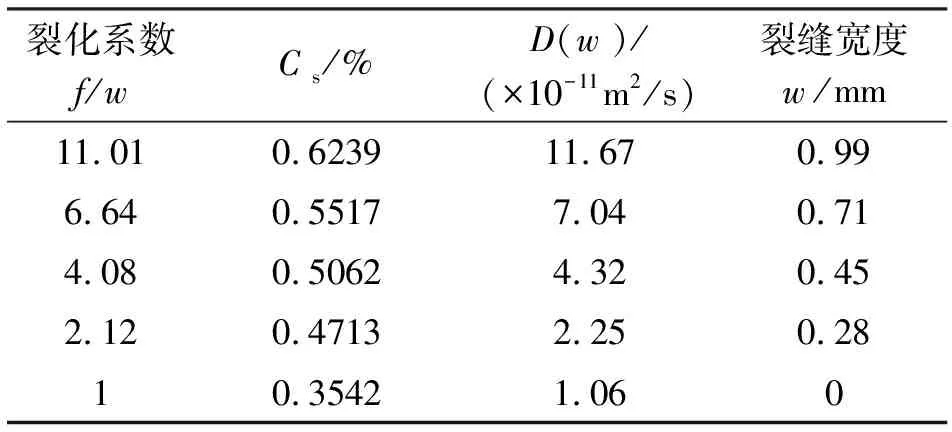
表4 非饱和状态下

由表可知，当裂缝宽度逐渐增大后，裂化系数f(w)也随之变大，根据该特点，将两种环境状态下的f(w)进行不同的曲线拟合，结果如图3所示。

(a)饱和状态下

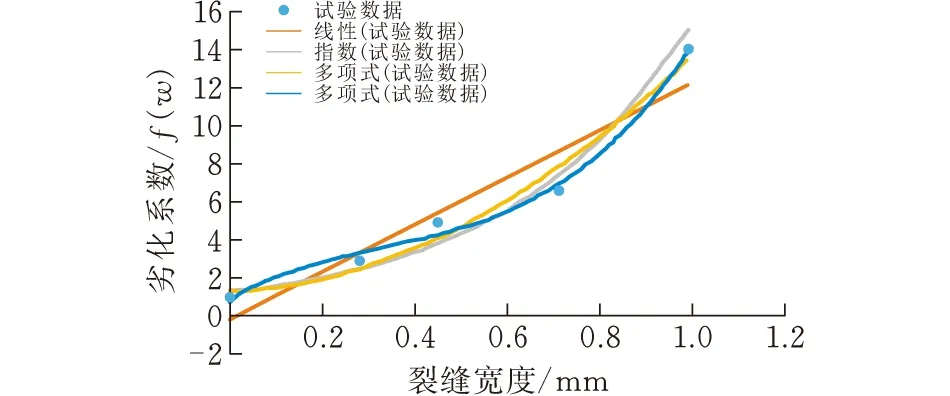
(b)非饱和状态下图 3 拟合结果

从上图可以看出，在这几种拟合结果中，线性拟合的结果与实际的结果有较大偏差，与实际的试验数据结果不相符。因此选取三次多项式拟合的结果，拟合模型表达式为

饱和状态：

f(w)=14.265w3-13.128w2+6.3548w+1
R2=0.9937

(3)

非饱和状态：

f(w)=23.656w3-23.634w2+13.305w+1
R2=0.9936

(4)

式中，R2为相关系数。

2 带裂缝混凝土的耐久性模糊可靠度研究

2.1 极限状态方程

一般来说，在沿海地区中，混凝土结构破坏的主要原因是氯盐作用。当混凝土长期暴露在这种环境中，氯盐，也就是氯离子会发生扩散。用Z表示结构的可靠度，可以得到极限状态下的可靠度方程为

(5)

式中，d为保护层厚度，Ccr为临界浓度。

非饱和状态下混凝土与饱和混凝土的区别在于饱和状态下是持续侵蚀，但两者均是以扩散为主。因此，非饱和状态下的侵蚀模型可以表示为

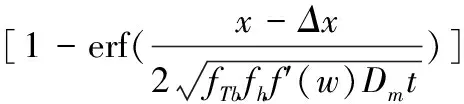
(6)

(7)

查阅文献[16]得知，Δx服从正态分布，其方差为0.92 mm，均值为3.76 mm。

同理，非饱和状态下的结构极限状态方程可以表示为

(8)

2.2 模糊可靠度分析方法

混凝土中的结构从可靠到失效往往是一个渐变的过程，并不是突然一下子发生的，中间存在的模糊区人们往往也是未知的，对于这个区域的研究，通常采用模糊可靠度分析方法。

(9)

其中，μA(x)指元素x隶属度的高低。

在工程函数中，隶属函数的形式较多且复杂难以计算。Monte-Carlo法可以通过计算机进行大量随机模拟实验，提高了计算效率，并且计算结果较准确。因此引入Monte-Carlo法，隶属函数形式为

(10)

式中，a表示抗力的初始值，b表示抗力的终值。

2.3 计算步骤

运用Monte-Carlo法对上述的参数进行一个统计，然后根据它们的特点运用Matlab生成n组数，当这些数逐渐增大到10000次时，发现最终的可靠度指标不再改变，逐渐稳定。所以最终n值取为10000，并代入式(3)，此时的失效概率Pf就是这n组数的平均值，即

(11)

可靠度指标则为

β=Φ-1(1-Pf)

(12)

3 混凝土耐久性模糊可靠度案例分析

3.1 算例

根据文献[18]中的铁山港特大桥，据了解，该大桥所处地带位于沿海地段，位于临海处它的底端结构出现了多处裂缝。结合上述对于混凝土的侵蚀模型进行分析讨论，并查阅相关文献[16,19]，得到基本变量的分布特征如表5所示。

表5 统计特征

3.2 计算结果分析

3.2.1敏感性分析通过上述修正的侵蚀模型，引入Monte-Carlo法对其进行模糊可靠度分析，最终运用Matlab生成w—β敏感性分析图。具体参数如图4所示。

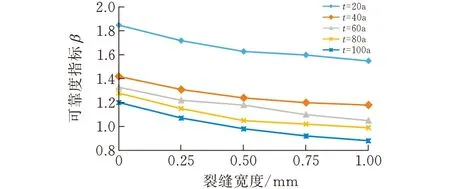
曲线(饱和)

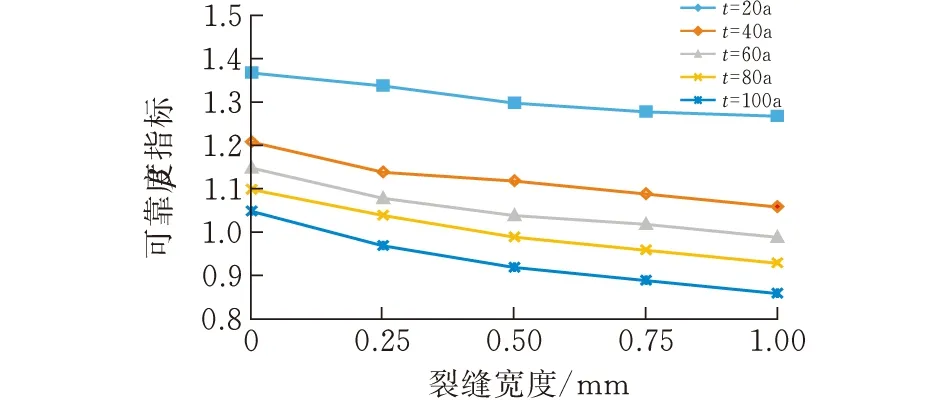
曲线(非饱和)图 4 w—β敏感性分析图

1)随着w增加，图a与图b的可靠度指标β逐渐降低，当w为0-0.3 mm时下降幅度较大；当裂缝宽度为0.6 mm之后，图像逐渐趋于平缓。

2)在饱和与非饱和状态下，服役时间t=100 a的可靠度指标最低，t=20 a的可靠度指标相对来说较高，并且在t=20 a到t=40 a之间，可靠度指标的下降跨度最大。

3.2.2混凝土结构耐久寿命预测取结构的目标可靠度指标为1.3[20]，给出相应的结构的耐久性寿命评估。

1)图5a、b为基于模糊可靠度得到的混凝土结构寿命预测，图5c、d为基于经典可靠度得到的混凝土结构寿命预测，两者的变化趋势总体上整体保持一致，整体呈现下降趋势，最终趋于平稳。

2)针对完整混凝土，也就是w=0 mm时，混凝土的可靠度指标最大；w=1 mm时，混凝土的可靠度指标最小。并且在20 a到40 a之间，可靠度指标的下降速率最快。

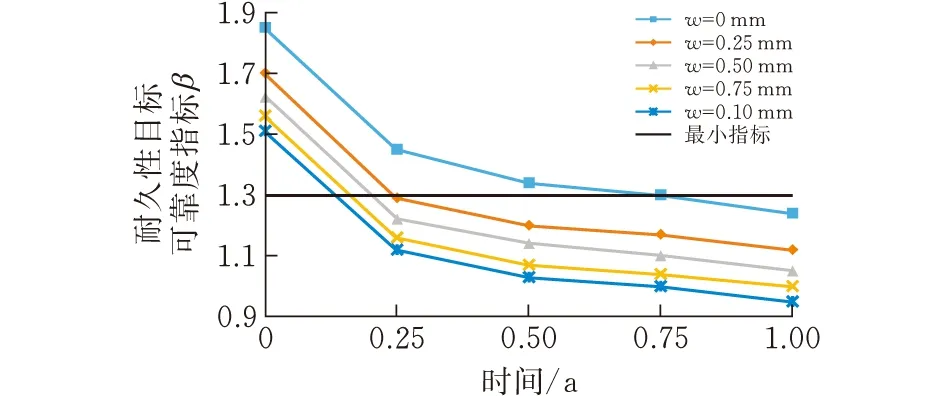
曲线(模拟海水区)

曲线(模拟潮差区)

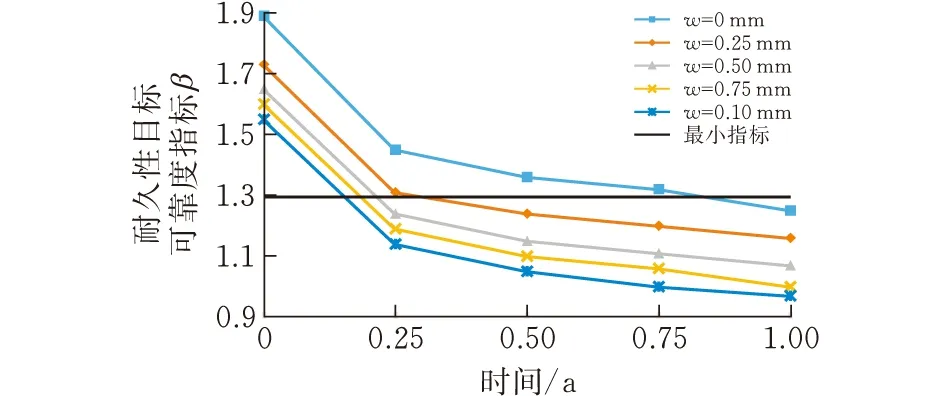
(c)t1—β1曲线(模拟海水区)

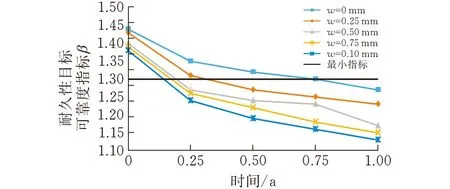
(d)t2—β2曲线(模拟潮差区)图 5 混凝土结构耐久寿命预测

4 结论

1)基于时间、温度、湿度及裂缝宽度为主要影响因素，提出了带裂缝混凝土在饱和状态、非饱和状态下时的氯离子扩散修正模型。

2)计算表明不管是饱和状态还是非饱和状态下的混凝土，当其裂缝的增加或者氯离子侵蚀时间的延长都会使混凝土的力学性能受到影响，降低结构的耐久性。

3)当取结构的耐久性目标可靠指标为1.3时，混凝土裂缝宽度w=[0mm, 0.25mm, 0.5mm, 0.75mm, 1mm]时，饱和状态下，对应的结构预测寿命t=[82 a, 41 a, 36 a, 34 a, 32 a]；非饱和状态下，对应的结构预测寿命t=[11.5 a, 7.7 a, 6.7 a, 6.3 a, 5.9 a]，本研究方法可以为工程结构的耐久性设计及评估提供参考依据。