非正交多址系统中基于Raptor码的下行传输设计与优化
张 昱,李 昊,彭 宏,卢为党
1(浙江工业大学 信息工程学院,杭州 310023)
2(东南大学 移动通信国家重点实验室,南京 210096)
1 引 言
当前移动通信系统面临着用户数量及其数据需求的快速增长,需要研究新型移动通信技术以应对上述挑战.非正交多址[1,2](Non-orthogonal Multiple Access,NOMA)技术是一种新型多址技术.在NOMA中,各用户可以占用重叠时频资源,接收端通过各类信号处理技术处理用户间干扰,可以有效提升频谱效率、服务用户数量等.
当前工业界以及学术界已经提出了多种NOMA方式,例如功率域非正交多址[3](Power Domain Non-orthogonal Multiple Access,PD-NOMA)、低密度蔓延[4]、稀疏码多址[5]、交织多址[6]、多用户共享接入[7]、图样分割多址[8]等.对于下行PD-NOMA而言,在发射机端,根据用户的信道状态为用户分配不同的功率,基站可以在相同的通信资源上广播叠加的用户信号.在用户端,可以采用串行干扰消除[9](SIC)技术消除来自其他用户的干扰,以获取用户自身所需的信息.
Liu Y和Chen Z等人将传统正交多址接入(Orthogonal Multiple Access,OMA)和PD-NOMA进行比较,并通过仿真表明,PD-NOMA都具有较好的总传输速率性能[10,11].因此,当考虑到高频谱效率和大规模连接性的需求时,PD-NOMA比OMA更有优势.目前已有一系列文献研究了PD-NOMA系统中的编码传输设计与优化.Chida Y等人研究了低密度奇偶校验码(Low Density Parity Check,LDPC)在PD-NOMA系统中的传输机制以及性能[12,13].Wang X等人提出了Turbo码和多用户检测联合优化的方法,显著提高了NOMA系统性能[14-16].Dizdar O等人提出了一种基于Polar码的NOMA传输方法[17,18],该方法可以在多路复用用户接收功率相似的情况下降低NOMA的误码率,对叠加编码功率分配具有较强的鲁棒性.
在NOMA中采用传统的固定速率信道编码面临以下挑战:一是发射端需要实时的信道状态信息反馈来确定信道编码码率,二是当接收端译码失败时采用混合重传机制(Hybrid Automatic Repeat Request,HARQ),这会进一步增加系统开销.Bonello N等人[19]比较了无速率码与固定速率编码,与LDPC码基于增量冗余的HARQ方案相比,Raptor码[20,21]能够提供更大的吞吐量,Raptor码能够自适应信道,并且在发射机处不具备实时信道状态信息(Channel State Information,CSI)下,仍能接近平均信道容量[22,23].Zhang Y等人表明,与使用固定速率编码相比,使用Raptor码可以显著地提升系统吞吐量[24].
本文主要研究以下内容:1)设计了块衰落信道下非正交多址系统基于Raptor码下行传输方案,首先,基站使用LDPC码作为外码将用户消息分别进行预编码,再通过LT码[25,26]作为内码编码,得到Raptor码码字,将码字经过调制后采用一定功率分配因子进行叠加编码后发送给每个用户,用户接收到信号后,对接收的信号进行置信传播(BP)译码[27,28],从而恢复出用户所需的信息;2)针对块衰落信道,提出了功率分配和Raptor码度数分布联合优化算法.通过外信息传递分析(Extrinsic Information Transfer,EXIT)译码过程,以最大化系统平均传输速率为目标,仅依据系统统计信道信息(CSI),对各用户无速率码度数分布和基站功率分配进行联合优化.通过仿真验证优化得到的结果具有较好的误码率及传输速率性能.
2 系统模型
如图1所示,本文考虑两用户下行NOMA系统,在该系统中,基站与两用户之间进行下行通信,hi表示用户i(i∈{1,2})到基站的信道增益.
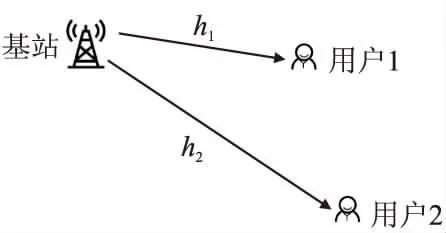
图1 系统模型
我们假设各节点间链路经历块衰落,各链路的信道增益在每轮的信息传输期间保持恒定,在各轮之间是独立且随机变化的,满足一定的概率分布.对于接收方两个用户而言,基站到本用户的信道状态信息是已知的.而利用无速率传输,基站并不需要知道当前信道信息.在每一轮传输过程中,基站持续将信号传输给两个用户,直到两个用户正确译码恢复信息并反馈确认(Acknowledgement,ACK)为止.每轮传输的详细过程如下:
首先,在发送端基站处,对用户i长度为K的消息mi进行Raptor编码(两用户消息长度一致),以获得编码比特ci,然后经过调制得到信号xi,i∈{1,2},注意,由于基站无法获得实时CSI,Raptor码的度数分布是固定不变的.
基站将用户i,i∈{1,2}的信号进行叠加编码,得到发送信号:
(1)
其中分配给用户1信号的功率P1为:
P1=(1-α)P
(2)
分配给用户2信号的功率P2为:
P2=αP
(3)
其中P表示基站的总发送功率,α表示功率分配因子.
用户i(i∈{1,2})收到的信号分别为:
(4)

两用户采用SIC以及BP译码恢复所需信息.当成功恢复后,用户会反馈ACK,以通知基站停止本轮传输.
3 非正交多址系统下行Raptor码传输方案
3.1 Raptor码编码方案
基站将各用户下行信息先通过LDPC编码器进行Raptor码的预编码,再进行LT编码.基站对各用户信息向采用相同的LDPC编码,但LT码各不相同.对于用户i(i∈{1,2})来说,Raptor码度数分布为:
Ωi(x)=Ωi,1x+Ωi,1x2+…+Ωi,DxD
(5)
其中i∈{1,2},Ωi,k是用户i码字比特度数为k的概率,k=1,…,D;
每个码字比特按如下方法生成:首先,根据度数分布随机选择每个码字比特的度数.对于度数为d的码字比特,从LDPC预编码码字中随机选择d个比特,进行异或运算.通过上述编码过程,可以无限生成随机码字比特.为简单起见,采用二进制相移键控调制(Binary Phase Shift Keying,BPSK),即将Raptor码字比特0和1映射为发送符号1和-1,以此得到各用户i的发送信号xi.
3.2 用户端基于SIC的BP译码
传输开始前,各用户从基站处已经获知Raptor码度数分布以及功率分配因子.事实上,由于两者在所有传输轮次中保持不变,基站只需告知一次,信令开销极小.我们首先对功率分配因子α>0.5的情况展开讨论.此时由公式(3)可知,基站叠加编码时对用户2分配更多的功率.另一方面,基站发送给各用户的消息长度相等,因此对各用户消息的实际编码速率是相等的.在各用户处,用户2信息对应的信干噪比更大,更容易被恢复.因此用户1需要利用SIC,先恢复用户2的信息,再将其从接收信号中去除,然后恢复用户1自身的信息.
对于用户1而言,用户1从接收信号中获得关于x2的对数似然比(Log-likehood Ratio,LLR)表示为:
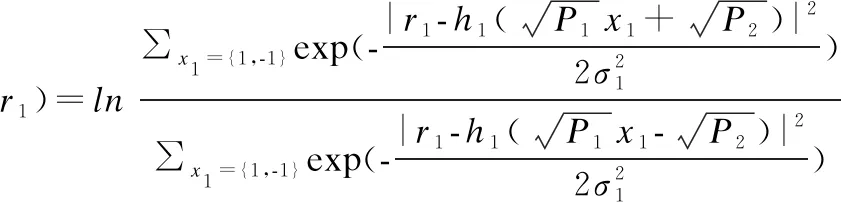
(6)
基于式(6)的LLR,用户1采用BP译码恢复用户2消息.在BP算法中,“消息”在变量节点和校验节点之间沿着其相连边进行交换.每个“消息”是由该边连接的相应变量节点的LLR.整个译码过程中可分为两个阶段.如图2所示,在第1阶段,对整个译码图执行译码迭代,直到输入节点的平均LLR超过预定阈值mth,这是LDPC成功译码的最小要求.该阈值可以通过Peng H等人提出的方法[29]获得.在第2阶段中,在上半部分LDPC子图上单独执行译码迭代以去除残留误差.下面给出第一译码阶段的详细过程,对于l次迭代:

图2 Raptor码译码图
步骤1.从输入节点i到LDPC校验节点c的消息是:
(7)
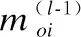
步骤2.从LDPC校验节点c到输入节点i的消息是:
(8)
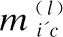
步骤3.从输入节点i到LT输出节点o的消息是:
(9)
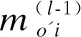
步骤4.从LT输出节点o到输入节点i的消息是:
(10)
其中z为根据LLR公式(7)计算出的的信道LLR消息.累乘部分是除本身之外的所有与LT输出节点o相邻的输入节点.
步骤5.在输入节点i的LLR更新如下:
(11)
第2阶段,在每个用户的LDPC译码图上单独执行消息交换.该阶段的具体过程与步骤1-步骤2类似,不再进行赘述.
当译码迭代达到最大次数或译码满足LDPC码的所有校验约束时,译码终止.
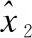
(12)
(13)
由此得出关于x1的LLR,表示为:
(14)
用户1利用上述LLR再进行BP译码来恢复本用户信息.
另一方面,对于用户2而言,无需采用SIC,直接利用BP译码恢复本用户信息.用户2从接收信号获取的关于x2的LLR为:
(15)
最后,对功率分配因子α<0.5的情况,此时用户2需要进行SIC而用户1不需要.对于功率分配因子α=0.5的情况,由于各用户消息的实际编码速率相等,各用户都不需要SIC.
4 Raptor码输出度数分布设计
4.1 译码过程的EXIT分析
首先我们分析用户BP译码过程中外信息传递(EXIT)过程[30].这里的外信息指的是编码比特(或等效的编码符号)与其LLR之间的互信息.
如图3所示,我们以α>0.5时,用户2恢复本用户信息的BP译码过程为例,对于第l轮迭代:
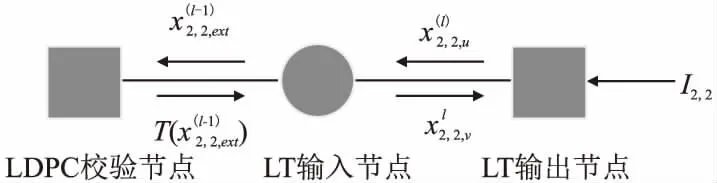
图3 Raptor译码图外信息传递过程
步骤1.LLR消息从LT输入节点传送到LDPC校验节点,其携带的平均外信息为:
(16)
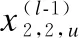
(17)
步骤2.从所有LDPC校验节点到输入节点的平均外信息是:
(18)
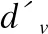
步骤3.输入节点到输出节点的平均外信息是:
(19)
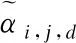
步骤4.输出节点到输入节点的外信息更新:
(20)
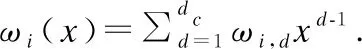
同样地,我们可以得到用户1译码用户2信息的外信息更新过程为:
(21)
以及用户1进行SIC后,译码本用户信息的外信息更新过程为:
(22)
上述各式中,I1,2和I2,2分别表示用户1(用户2)从原始接收信号中(即不是SIC后的信号)获得的关于x2的LLR所对应的外信息,即:
Ii,j=I(xj;L(xj|ri))
(23)
其中i∈{1,2},j∈{1,2},我们可以根据蒙特卡洛法获得上述互信息,具体过程描述如下:以用户2直接译码x2,即获得I2,2为例.首先,设置基站发送的用户2信号x1为1,用户1信号x1随机等概率地产生1或-1.根据公式(4)产生高斯噪声以此得到r1和r2.根据公式(6),我们可以得到L(x2|r2).通过生成大量的随机样本,利用蒙特卡洛法我们可以近似得到概率密度P(L(x2|r2)|x2=1).利用类似的方法,当我们可以得到其余的条件概率密度,以此近似地计算出式(23)的互信息.另一方面,对于用户1从SIC后的信号获得关于其本身所需消息的信道输出外信息I1,1可以根据式(14)和式(17)直接计算获得.
4.2 度数分布优化
基于上述EXIT分析,我们联合优化各用户Raptor码度数分布以及基站功率分配因子.目标是在保证每轮各用户成功译码基础上,最大化平均下行总传输速率,在发送消息长度固定下,等价于最小化平均码长.
在每一轮传输过程中,基站向两个用户连续发送叠加编码码字,直到两用户成功译码出各自的信息.我们以α>0.5为例,用户1恢复用户2消息所需的码字长度可以表示为:
(24)
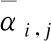
类似地,用户1恢复本用户消息所需的码字长度为:
(25)
用户2恢复本用户消息所需的码字长度为:
(26)
基站所需传输的码字长度为上述三者的最大值,即:
t(H,α)=max(L1,1,L1,2,L2,2)
(27)
通常,信道矩阵空间H是连续的.为了建立可解的优化问题,我们将空间离散为Q状态:Hq,q=1,…,Q.每个状态出现的概率表示为Pq.平均码长表示如下:
(28)
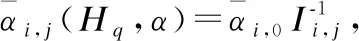
(29)
由于α取值影响到用户端的SIC过程,影响其成功译码条件,因此需要分情况讨论.对于α>0.5:
(30)
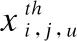

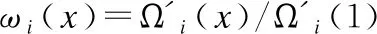
5 仿真结果
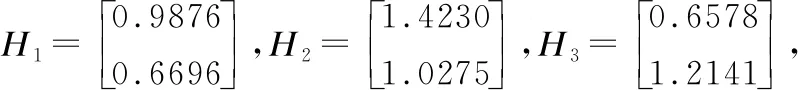
5.1 BER性能
首先,分别仿真了以上3种信道状态下的误码率.基站的总发送功率为P=2.5.
通过上一节的联合优化方法,得到功率分配因子α=0.64以及各用户最优度数分布为:
Ωopt1(x)=0.0127x+0.3961x2+0.3044x3+0.0845x6+
0.1062x7+0.0678x17+0.0174x18+0.0109x60
(31)
Ωopt2(x)=0.0127x+0.3914x2+0.3199x3+0.0664x6+
0.1220x7+0.0843x17+0.0113x60
(32)
此外我们还仿真了二进制擦除信道(Binary Erasure Channel,BEC)下的最优度数作为对比方案:
ΩBEC(x)=0.0008x+0.494x2+0.166x3+0.073x6+0.083x7+
0.056x17+0.037x60+0.056x19+0.025x65+
0.003x66
(33)
我们仿真了不同译码开销下的两用户总误码率.当α>0.5时,译码开销定义为:
(34)
其中N是基站实际发送的码长,K是用户消息长度,min(I1,1,I1,2,I2,2)/K是由信息论所得基站理论所需发送码长.更大的译码开销意味着基站发送更长的码长,即等价于更低的实际传输速率.开销为0即为理论上限.图4-图6这3个图分别给出度数优化以及BEC度数在信道矩阵H1、H2、H3下的误码率.值得注意的是,尽管本文方法针对平均系统性能优化Raptor码度数分布,但其在各信道状态下的误码率性能仍然很好.与BEC度数分布相比,达到相同误码率下的开销更小.

图4 信道矩阵为H1的误码率
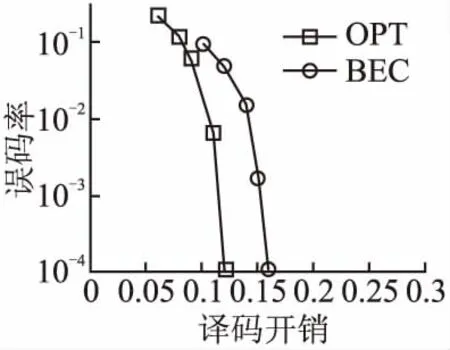
图5 信道矩阵为H2的误码率
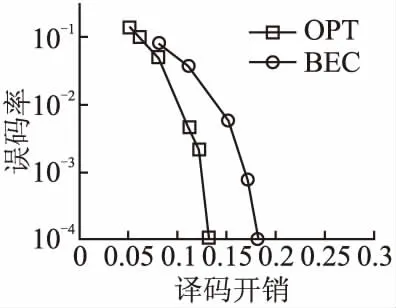
图6 信道矩阵为H3的误码率
5.2 吞吐量性能
我们仿真了在不同信噪比下的系统平均传输速率.对于不同的信噪比,我们固定噪声功率,调整基站总发送功率P.我们在各信噪比下分别优化了Raptor码的度数分布以及基站功率分配因子.仿真结果如图7所示,除了本文提出的优化方法,我们还考虑两种对比方法.
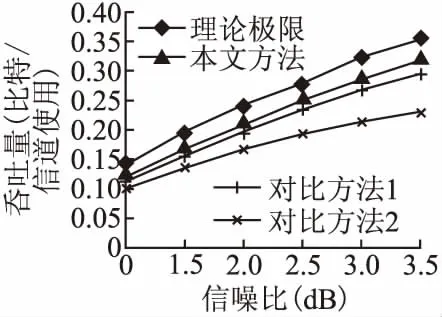
图7 本文方法与其他对比方法的系统下行吞吐量
对比方法1.基站对于两用户信息的Raptor编码采用公式(33)给出的BEC最优度数分布,功率分配因子按下述方法获得:固定优化问题公式(30)中的边度数分布{ωi,d}为BEC最优度数分布对应的边分布,然后利用穷举搜索求解该问题,得到边度数分布固定下的最优功率分配因子α.
对比方法2.基站对于两用户信息的Raptor编码采用与按本文方法优化的度数分布,但功率分配因子选取α=0.5.
对于图4-图6中的每个点,仿真了100轮的传输,每轮都是从H1、H2、H3中均匀随机选取信道矩阵.从图中可以看出,通过与各方法对比的结果显示,优化的Raptor码度数分布以及优化的功率分配因子都能带来传输速率的提升,且优化后与信息论理论极限相差11%左右.
6 结 论
本文设计了块衰落信道下非正交多址接入系统中两用户下行场景的Raptor码传输方案.为了最大化系统平均传输速率,本文基于外信息传递分析(EXIT)提出了功率分配和Raptor码输出度数分布联合优化的设计方法.计算机仿真结果表明,基站采用本文的优化方法获得的功率分配因子以及Raptor码度数分布,能够达到降低系统误码率,并提高系统平均下行传输速率的效果.

