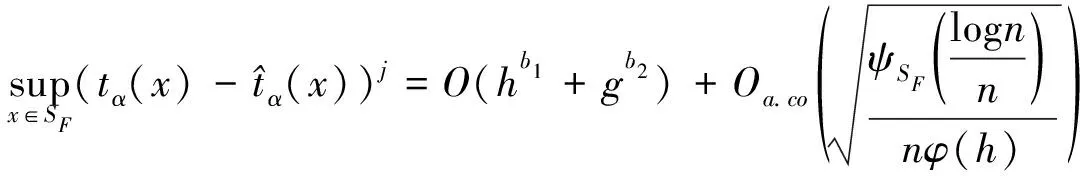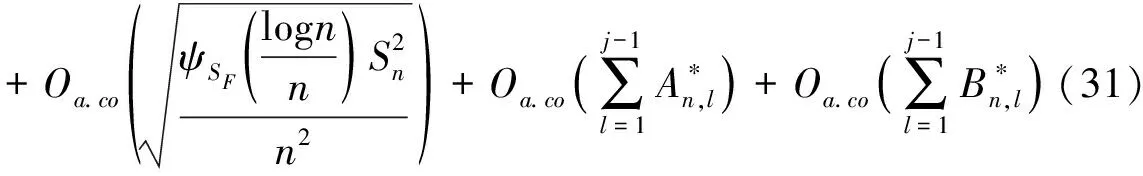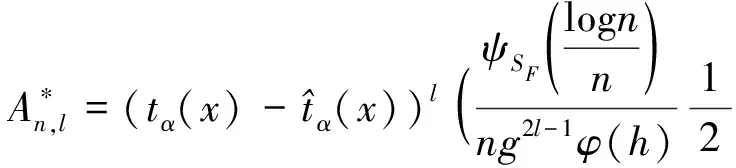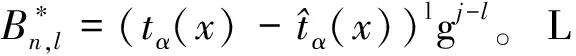相依函数型数据条件分位数估计的渐近性研究

丁 洁， 余新宏

(安徽农业大学 经济技术学院，安徽 合肥 230001)

众所周知,条件分位数在许多领域都有着广泛的应用,条件分位数估计是非参数分析的一个非常重要的问题。就条件分位数估计的非参数估计问题而言,通常来说也如同条件均值估计、条件密度估计一样,存在解释变量

X

取值于

R

空间,相应的响应变量

Y

取值于

R

空间的情形。此外,样本(

X

,

Y

)通常被认为是独立同分布,或者是具有某种相依性的随机变量。

随着国内外对统计的重视程度不断提升,人们开始收集金融、医疗等领域的数据,开始对函数型非参数统计进行全方面研究,早期在文献[8-11]中有详细研究,上述文献详细讨论了独立同分布或者某种相依场合下估计量的逐点收敛性。特别的,在独立同分布的条件下,文献[9]利用Kolmogorov熵的方法讨论了统计学各估计量,条件累积分布,条件风险率函数的一致收敛性。然而由于条件分位数在金融等领域的广泛应用以及时间序列的相依性,本研究利用Kolmogorov熵的方法获得条件分位数的几乎完全一致收敛性,将独立同分布的情形推广到相依情形,同时将逐点收敛性推广到一致收敛性。

在本研究中设为半度量空间的子集,数量为的Kolmogorov 熵。为算术混合,且速度。设(

X

,

Y

)1≤≤同分布于(

X

,

Y

),这里

X

取值于有半度量的抽象无限维空间(

F

,

d

),

Y

取值于

R

空间。全章

C

,

C

′,

C

以及为正常数,并且分别在不同的情形下取不同的值。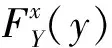

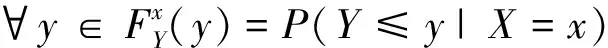
相应的条件分位数记为

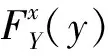
(1)

和

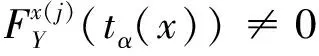
(2)

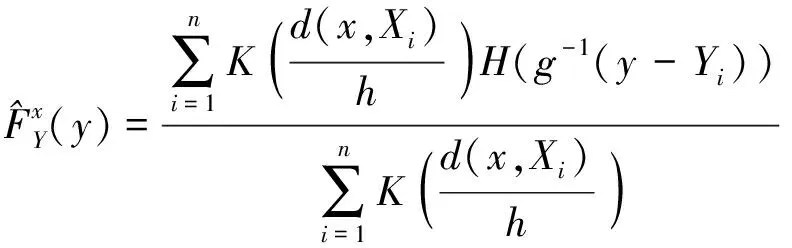
(3)

H

为

j

次连续可微函数,并且满足

H

′=

K

。这里,

K

和

K

为实值非负核函数。光滑算子

h

=

h

,

g

=

g

均为正实数列,并且当时

n

→∞,趋向于0。

1 基本假设

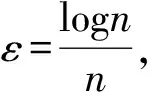
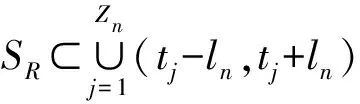
这里

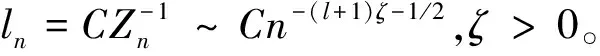
(4)

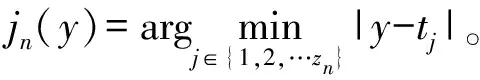
上述思想主要采用文献[8]中引理6.17和引理11.17的做法。

此外,对于任意的

l

∈{0,1,2,…,

j

},记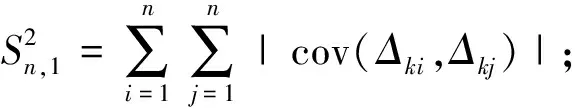

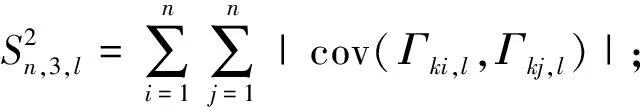
这里,

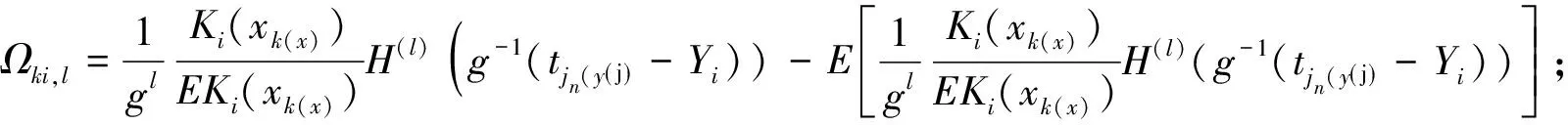
此外, 为得到本章主要结论,引入一些常用的假设。

关于小球概率,假设,

(H1)∀

x

∈

S

,0<

Cφ

(

h

)≤

P

(

X

∈

B

(

x

,

h

))≤

C

′

φ

(

h

)<∞,这里,当

h

→0时

φ

(

h

)→0。(H2)函数

φ

(

h

)满足(

nφ

(

h

))=

O

(log

n

)。

关于核函数

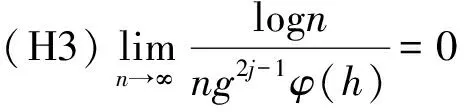
K

和

K

,假设(H4)

K

是紧支撑集[0,1]上的非负有界核函数。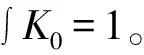

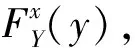
(H6) ∀(

x

,

x

)∈

S

×

S

, ∀(

y

,

y

)∈

S

×

S

,对于某个

b

>0和

b

>0，

(5)

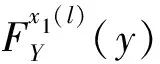
有关相依结构,假设

(H7)∃

θ

>

C

β

+1>2,对于任意给定的∀

l

∈{0,1,2,…,

j

},满足,

(6)

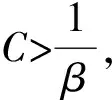
注:假设(H1)～(H6)详细情况可参见文献[8]。与独立同分布情形相比,条件(H7)为相依结构的影响。

最后,关于

S

上的Kolmogorov熵,引入文献[9]中所用的假设,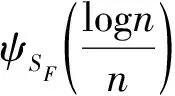

(H8a) 当

n

充分大时,

(H8b)对某个任意给定的

β

>1,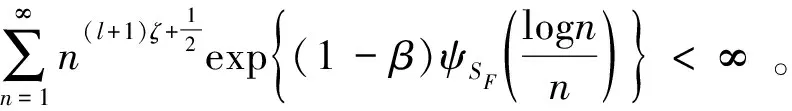

2 引理证明

引理1: 在条件(H1)～(H8)下,对于

l

=1,2,…,

j

,得出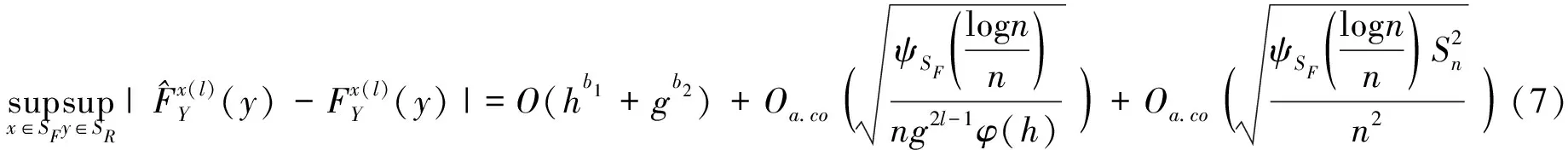

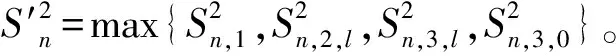
引理2:在条件(H1)～(H8)下,我们有

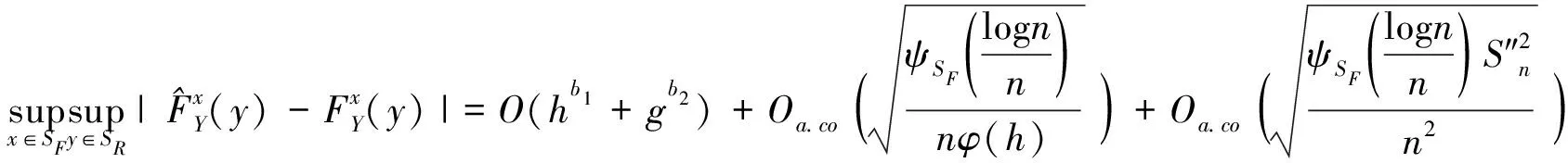
(8)

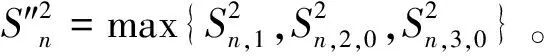
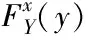
引理1的证明:这里的证明利用了Ferraty等证明方法。 具体有如下分解:

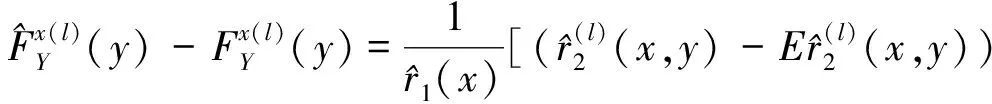
(9)

这里,

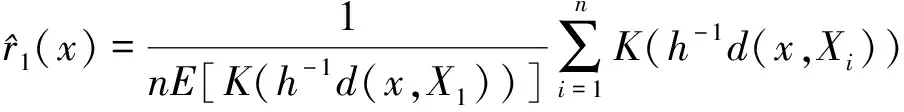
(10)

并且,

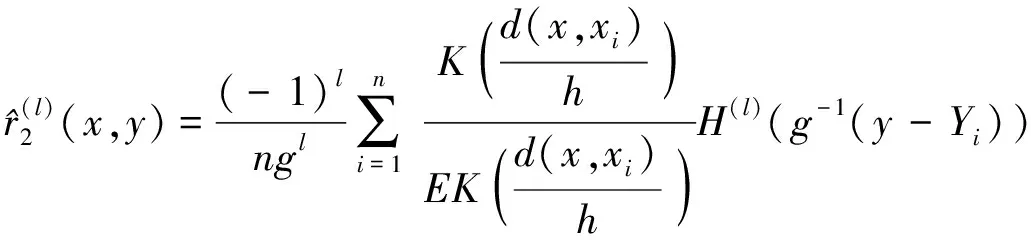
(11)

这里,需要证明:

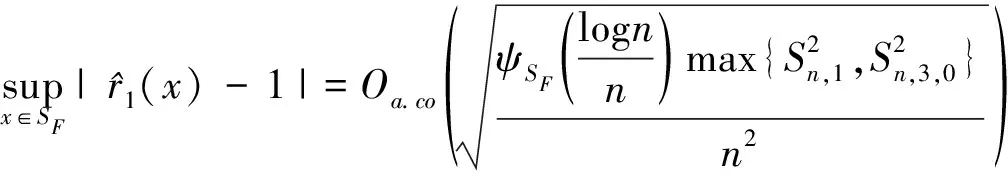
(12)

(13)

并且,

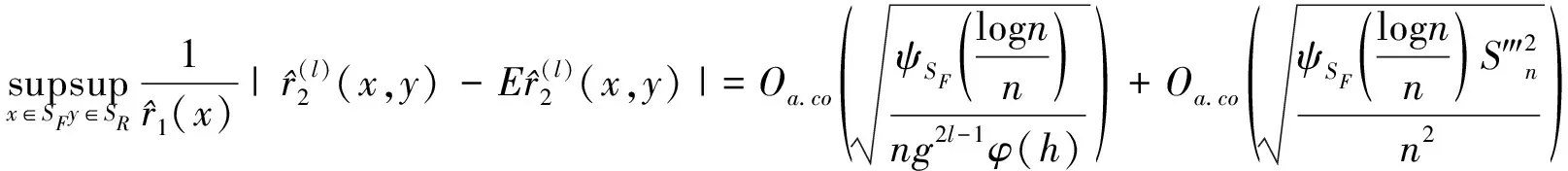
(14)

首先证明(12)式,由于,

(15)

关于

F

,对于任意

n

>0,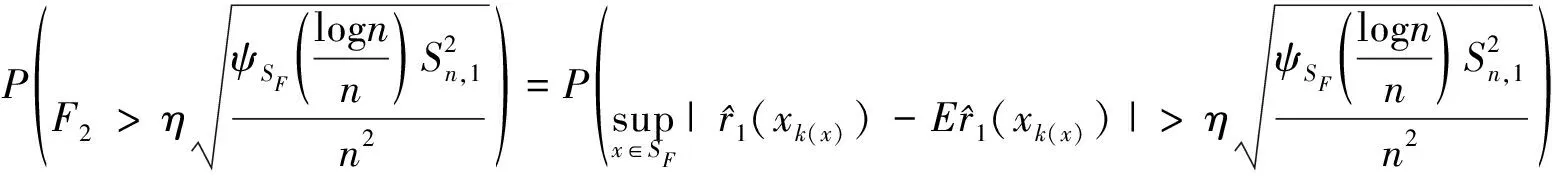

(16)

由文献[8]中命题A.11 ii)以及Kolmogorov熵的定义,取

r

=log

n

>1,对某一个正常数C<∞,得出,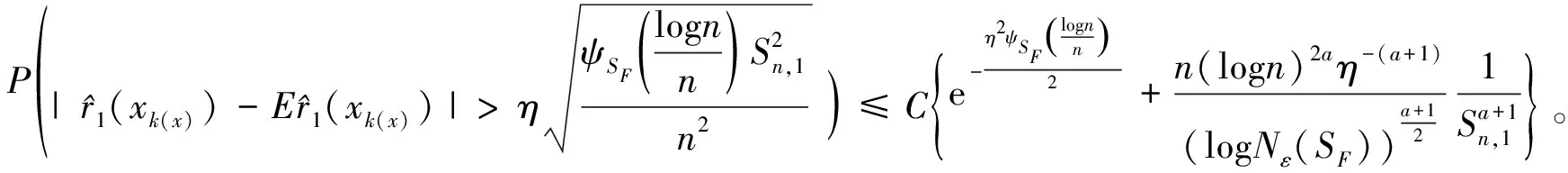

进一步,由(6)式,得出

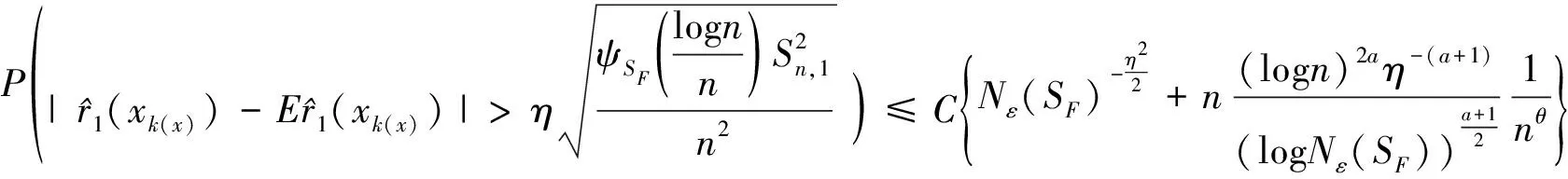
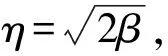
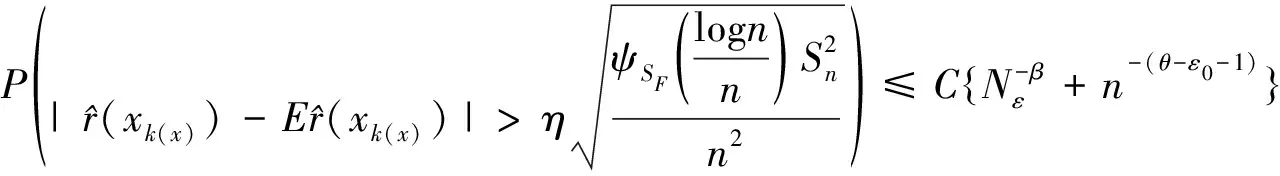
(17)

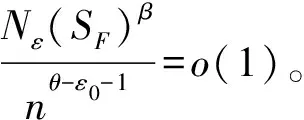
因此,由(16)和(17)式,

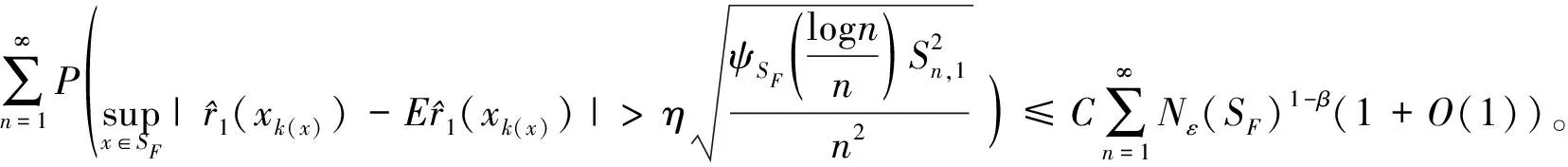
根据条件(H8b),得出

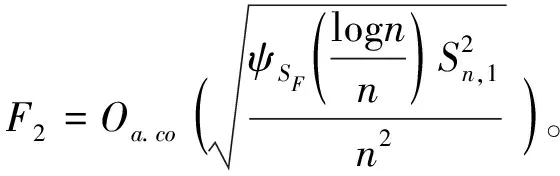
(18)

对于

F

, 由条件(H1)(H4)以及(10)式,

由此可以推出,

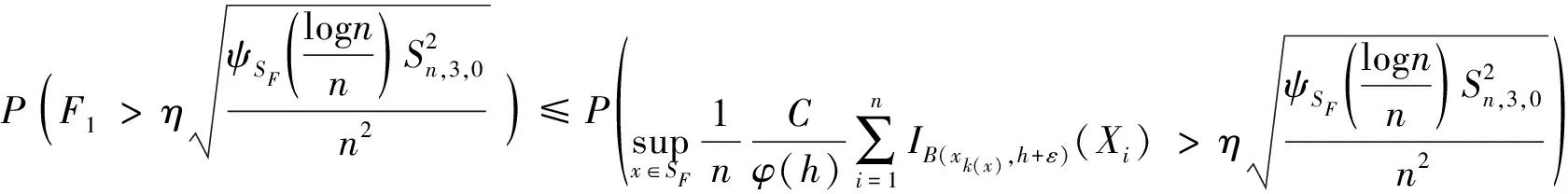
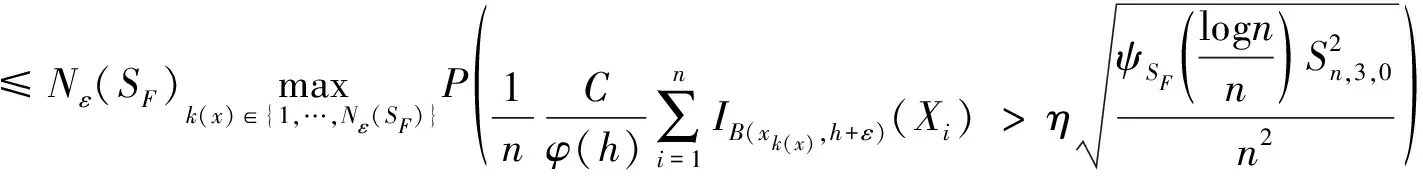
接下来,利用和的证明的同样的步骤,得出

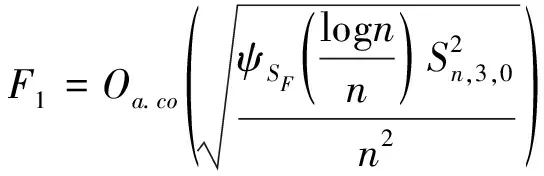
(19)

最后,类似的

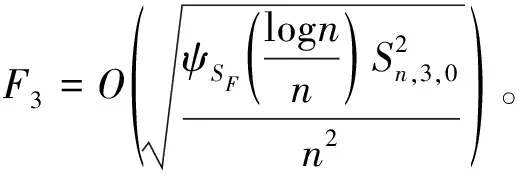
(20)

由(15)式以及(18)～(20)式,(12)式成立。

关于(13)式的证明。 由于

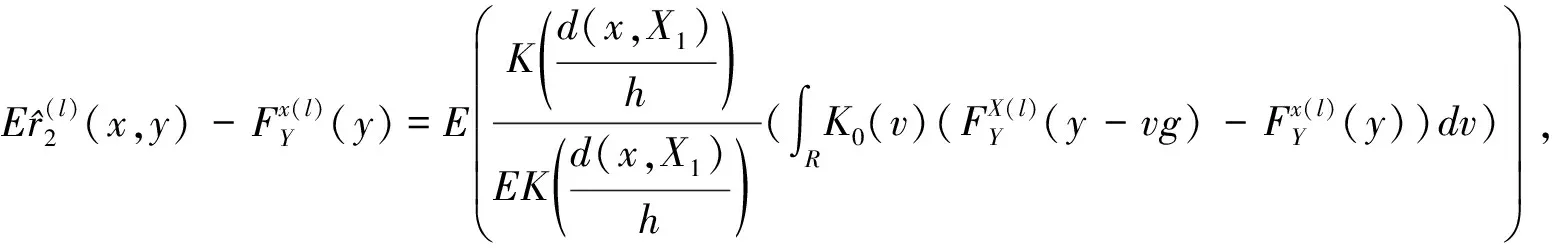
由(5)式,显然(13)式成立。

最后证明(14)式。证明主要是基于如下分解:

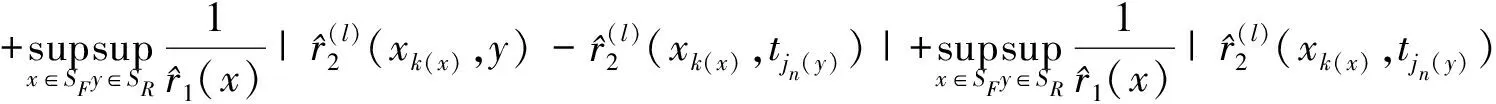
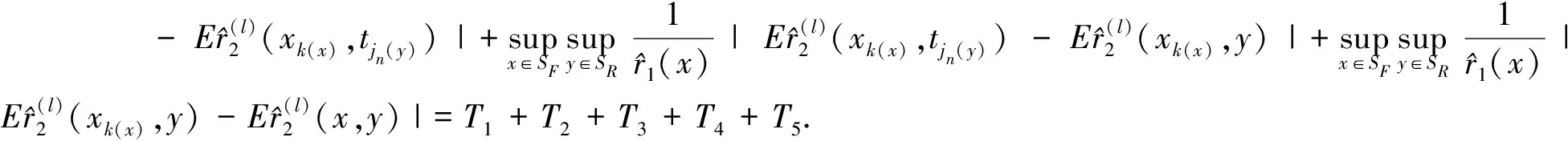
(21)

对于

T

,由于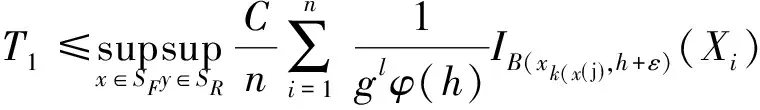

类似于的证明,可以得到

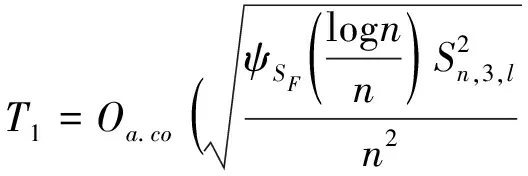
(22)

同理,

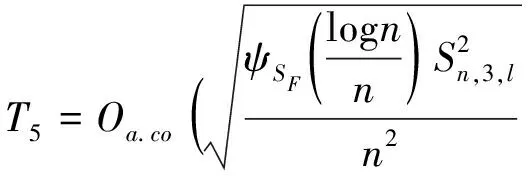
(23)

对于

T

, 由于

H

的连续可微性,得出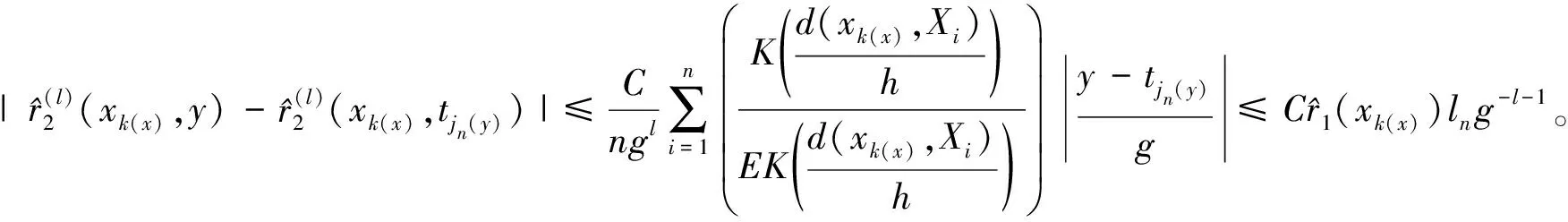

由假设条件(H3) 以及(4)式,得出

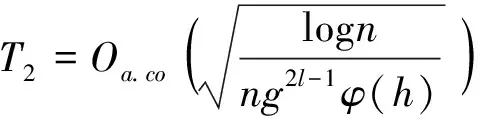
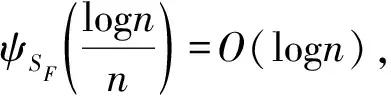
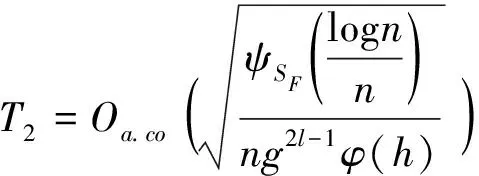
(24)

类似于的证明,得出

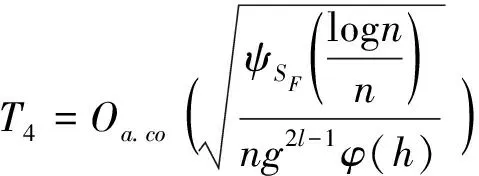
(25)

关于

T

,类似于

F

的证明并且由条件(A8b),得出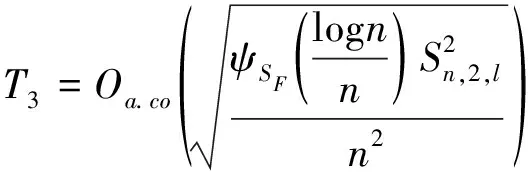

(26)

最后,由(21)-(26)式,等式(14)成立。

引理2的证明:根据文献[8]中的分解:

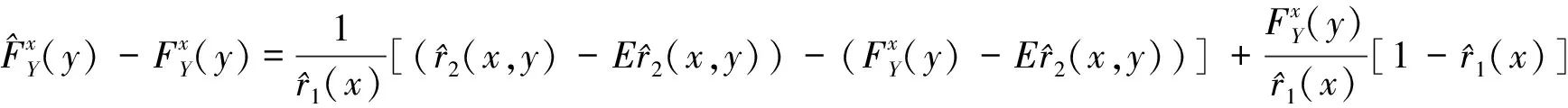
(27)

因此,只要下面的两个等式成立以及结合前面所证明的(12)式:

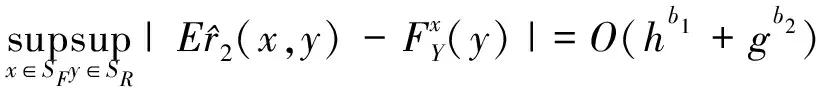
(28)

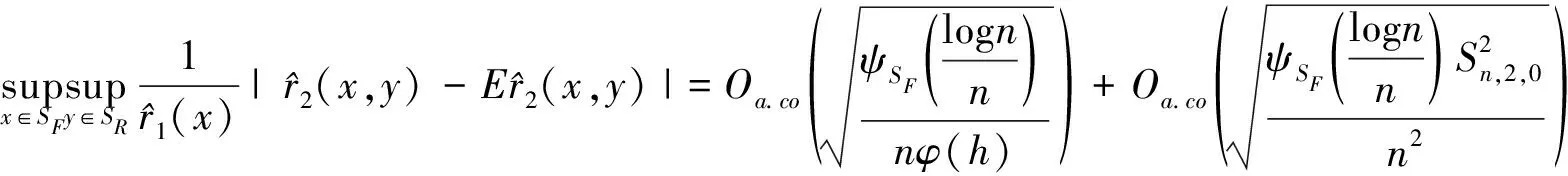
(29)

事实上,

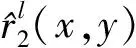
3 定理证明

定理:在条件 (H1)～(H9)下,得出

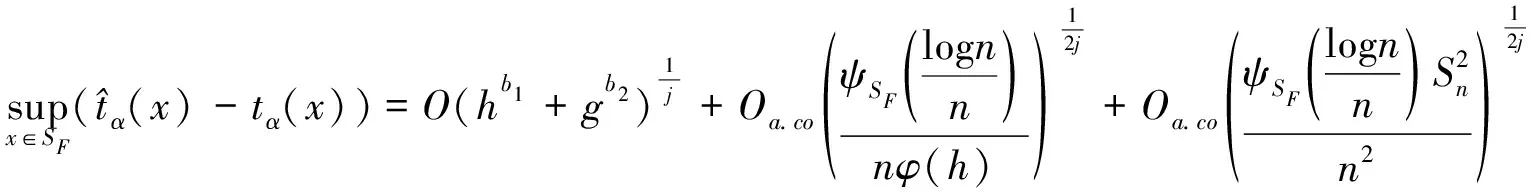
(30)