中低纬度下惯导极区性能模拟测试方法
文 者,卞鸿巍,马 恒,*,臧 涛
(1.海军工程大学电气工程学院,湖北 武汉 430033;2.海装武汉局驻武汉地区第二军代室,湖北 武汉 430064)
0 引 言
近年来,随着极地地区自然环境的开发,人类在极区领域的活动日渐频繁,极区航线不断开拓。极区导航能力成为船舶、飞机在极区航行过程中的重要科技支持。
由于惯性导航系统独有的自主性、优良的可靠性,极区惯性导航成为研究的重点,而经线收敛、地球自转矢量与重力矢量趋于共线等问题,使得中低纬度适用的传统编排惯导算法失效[1]。针对此问题,前人也做了大量研究,主要有基于横向坐标系[2-4]、格网坐标系[5-6]、平面坐标系或地球坐标系[7]等编排的极区惯导算法,以及基于游移力学编排的算法、全球导航的算法设计[8],各种极区编排算法的有效性都得到了验证,并发展出了与之相关的阻尼算法、初始对准算法等,理论上已经比较成熟。
在对导航系统设备进行性能验收评估中,实地测试是不可或缺的环节,对于需要检验极区性能的导航系统也是如此。然而由于极区环境恶劣,实测获取数据难度大。北极地理位置遥远,大规模全面实地性能测试试验成本高,存在诸多现实困难。因此,需考虑被试导航系统采取中低纬度模拟测试的方法,即根据中低纬度被试导航系统输出的导航参数评估其在极区相似运动过程中的精度性能。迫切需要在中低纬度为导航系统极区性能指标的综合评价建立一套相对完善的评估体系,这将对降低极区惯导性能实地测试难度、节省实测成本,以及极区惯性导航系统设备研制、测试、应用等提供技术支持。
对于模拟测试领域的研究相关文献较少。其中文献[9]主要讨论了构造“虚拟极点(极区)”方法,即在中低纬度试验地区定义伪极区,在此区域采用游移编排格网导航算法验证算法的有效性。但是虚拟极区和实际极区存在差别:一是地球自转轴不会随虚拟极区的设定而改变,无法模拟重力矢量与地球自转矢量共线带来的影响;二是由于地表曲率不同,在极区对于船舶等在海平面运动的载体而言轨迹将不再贴合地表,无法重复其在中低纬度的运行轨迹;三是对于重力异常等引起误差的因素,极区与中低纬度的条件也不相同。综上,虚拟极区方法能利用一段中低纬度航次对极区算法进行验证,但进行系统误差的定量分析存在困难,尚不能用于评估极区实地的精度性能。文献[10]则采用了旋转地心地固坐标系实现轨迹的转移,但由于受到地表曲率不同的影响,轨迹转移到极区后仍需投影回地表,同样为后续误差分析增加了困难,使得该方法仍仅适用于算法验证。文献[11]比较了极区与非极区条件下横向导航算法的性能,文中部分提及中低纬度到极区的轨迹移植与惯性测量单元(inertial measurement unit,IMU)数据补偿方法,但其主要对横向坐标系地理适用性进行研究,研究由中低纬度数据生成极区数据,尚未系统深入地研究模拟测试具体方案。
在传统惯导精度性能测试中常使用的高精度惯性导航系统/全球导航卫星系统(inertial navigation system/global navigation satellite system,INS/GNSS)组合导航作为测试基准,目前在经典卡尔曼滤波技术[12]基础上发展出多种改进技术[13-16],组合导航的精度和可靠性得到进一步的提升,可作为中低纬度惯导模拟测试的基准系统。
本文分析了前人工作局限,在中低纬度实测试验中以高精度惯导与卫导的组合导航系统作为测试基准,研究以极区坐标系为媒介,轨迹基准设计上把直接移植改换成推算的方法,从而避开地球曲率对轨迹产生变形而需要重新投影、近似等的复杂过程。基准轨迹的推算产生方式保持了与惯导解算过程的机理相近性,也为简化后续定量误差分析等工作提供了较好的模型基础。最终本文提出了以“轨迹转换过程中横向坐标系下的姿态速度不变”为原则,在极区规划与载体中低纬度运行的相似航迹,详细推导了坐标转换和相关变量计算公式。针对其中IMU转换公式的数据来源问题,提出了以高精度INS/GNSS组合信息为基准的极区模拟测试方法,并通过仿真试验检验了理论算法的有效性。
1 极区模拟测试基本理论
极区横向编排的惯导解算方法已较为成熟,在此不再对横向坐标系、惯导横向编排加以赘述,本文所述的横向坐标系是以90°E与赤道交点为横北极点、本初子午线为横向赤道构成的横向坐标系,详细定义见文献[17]等。以下针对极区模拟测试轨迹转移原则及方法、转换过程相关变量的表示、IMU数据转换方法进行讨论。
1.1 轨迹转移方案
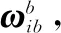
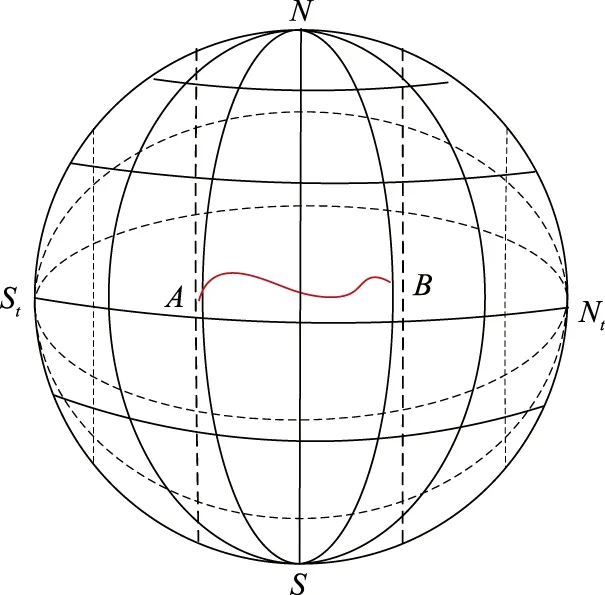
图1 中低纬度轨迹示意Fig.1 Trajectory of middle and low latitudes
要把这段过程转移到极区来进行,往往考虑采用两类策略:一是转换前后保持地理坐标系下航向不发生变化;二是尽量减小轨迹形状变形,设法将轨迹移植到极区。对于前一种方法,理论上分析简单,转换公式推导也相对容易,但是在极区时刻与中低纬度轨迹保持传统航向一致,势必会对速度进行压缩,轨迹也会发生严重压缩变形,特别是在近极点,速度趋于0,将无法完成模拟测试任务。对后一种方法,若中低纬度与极区的轨迹相似,考虑到横向坐标系的特点,因此采用横向姿态速度不变的转换原则以达到目标。首先应当进行参数的坐标转化。
1.2 极区模拟测试的初始化
1.2.1 速度、姿态、起始位置的坐标转化
由于模拟测试过程采取横向编排的惯导解算,首先应先将传统地理坐标系下的参数转到横向参数以便于后续分析。

(1)
(2)

(3)
(4)
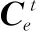
(5)
式中:φt和λt表示横向纬度和经度。
为计算同一点的地球坐标与横向地球坐标对应关系,即将坐标(φ,λ)转为(φt,λt)的公式如下:
(6)
方程推导从略。

1.2.2 模拟起始点位置的选定

(7)
在模拟测试中,模拟位置载体坐标系记为bm系,模拟位置当地横向地理坐标系记为tm系。
1.3 IMU数据转换算法
假设系统已按第1.2节内容在模拟极区设置了起始点,要模拟惯导系统在高纬度的运行,需要了解在相同的运动过程中IMU的输出有何变化。
1.3.1 加速度计输出数据补偿算法
捷联惯导速度更新方程(比力方程)为
(8)
式中:n为导航坐标系,如采用传统编排,n可改用g,即地理坐标系;如采用横向编排则可改为t或tm。
在实测和模拟地区都应满足比力方程:
(9)
由转换前后横向地理系下速度保持不变,横向地理系下姿态保持不变的前提条件,即
(10)
(11)

vt+gtm-gt}
(12)
1.3.2 陀螺仪输出数据补偿算法
捷联惯导的姿态更新方程可表示为
(13)
在实测和模拟地区都应满足姿态更新方程:
(14)
由式(10)和式(11),式(14)可作化简,其中:
(15)


(16)
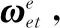
1.3.3 IMU转换公式中变量计算方法

(17)

(18)

东向速度和北向速度会对经纬度变化产生影响,令p和q分别为经度变化率单位矢量和纬度变化率单位矢量[2],则有
(19)
有关横东向速度、横北向速度对横经纬度变化的影响,可表示为
(20)
式中:R1、R2、R3可表示为
(21)
式中:a为地球长轴半径;e为地球偏心率。需要指出的是,在采用地球球体模型或近似计算时,可置地球偏心率e=0,从而舍弃掉较复杂的项,该变量最终表示为载体速度引起的横经纬度变化率:
(22)
Ctmt表示原横向地理坐标系到模拟地区地理坐标系的旋转关系,其计算可使用地球系过渡:
(23)
对于gt,使用达朗贝尔方程(WGS-84地球参数):
(24)
式中:g0=9.780 325 m/s2,为赤道海平面处的重力加速度;h为海拔高度。式(24)采用的是地理纬度,模拟测试解算中应进行横向地理坐标至传统地理纬度的转化。
2 模拟测试基准形成与方案设计
在模拟测试中,实测轨迹起点A点参数(位置、速度、姿态)应当以一定精度给定,其将影响模拟地区起始点A′点的惯导解算初始偏差。
2.1 模拟测试按基准情况的分类
在实际规划模拟测试的算法结构时,不同于普通测试的是,处理IMU数据转换时应根据基准的不同条件分为两类不同情况:一类是有基准情况,如在测试中中低纬度全部导航参数(姿态、速度、位置)均拥有较高精度的外部参考信息可作为基准使用,依此原则设计的模拟测试称为严格模拟测试(简称为严测试);另一种是无基准情况,认为除利用中低纬度起始点相关状态给定模拟惯导初值外,其后导航参数均无基准参考,完全依赖惯导自身解算值提供IMU转换公式中的中低纬度参数。依此原则设计的模拟测试称为宽松模拟测试(简称为宽测试),对于宽测试这种试验方法,中低纬度参数将采用惯导计算参数的形式代入IMU转换公式中,式(12)和式(16)改写如下:
(25)
式中:tc和bc表示中低纬度惯导计算机中相应的计算坐标系。显然,宽测试采用了测试惯导自身计算参数,后续对极区的模拟过程中复合了中低纬度导航参数计算误差,分析上带来了更大的困难,但其意义在于无基准条件下也可以进行轨迹等导航参数及IMU的粗转换,必要时可以根据IMU的属性估计出测试误差。
针对实际情况,对于设备的检验,往往设置一定的参考基准,在中低纬度对于速度、位置等设置高精度设备进行陪试。
同中低纬度测试相似,极区模拟测试中较常见地出现介于上述二者间的其他情形,如测试载体上装有GNSS信号接收机,则可视为位置的参考基准;实测过程中有白光测距仪进行工作,外部提供的速度是准确度较高的,则测距仪的速度信息可用作基准;测试载体安装有天文导航系统工作,航姿信息精度较高,则可用作姿态基准;或测试惯导旁存在更高精度惯导,则取基准导航参数为高精度惯导输出参数,等等。由此可见,实际模拟测试过程中少见全无基准仅纯测试惯导运行的情形,但也不能保证所有导航参数均设置有高精度基准参考,因此实际模拟测试情况往往介于上述两种分类之间,不再单独分类。
2.2 基准轨迹转移方法
中低纬度基准转移至极区形成基准,其中各时刻模拟位置速度基准、姿态基准与中低纬度时保持一致,可按照式(1)和式(2)给出,位置基准则可参考惯导位置更新的递推算法给出:
(26)
式中:起始位置为设定的极区起始点;T表示采样周期;纬度变化率、经度变化率参见式(20)。式(20)中的横向速度、横向经纬度变量可以k时刻模拟地区基准值代入。轨迹基准转化后,将生成一条模拟轨迹A′B′,如图2所示。

图2 极区模拟基准轨迹Fig.2 Polar simulation reference trajectory
图2中,实线表示传统北极地区经纬网,虚线表示横向纬线,其形状将与中低纬度轨迹AB相似。
2.3 基于高精度INS/GNSS基准的模拟测试具体方案结构设计
选取较高精度的基准以尽可能保证极区模拟测试的准确性是测试的必要条件,高精度INS/GNSS的速度、位置组合导航方式输出导航参数,其速度、定位精度均优于卫导精度,接近上文所述的严测试情形,且保持了惯导输出的连续性,可作为理想基准使用。
以高精度INS/GNSS组合导航方式为测试基准的极区模拟测试方案结构图如图3所示。图3中,以a、v、p分别表示导航参数姿态、速度和位置。

图3 极区模拟测试方案结构图Fig.3 Structure diagram of polar simulation test scheme
图3中测试惯导提供IMU数据,可无需进行当地解算;组合导航基准模块提供基准的姿态、速度、位置信息;坐标转换模块作用是将地理坐标系下导航参数转化为当地横向坐标系下,所用公式为式(1)~式(6);基准转换模块将中低纬度横向坐标系基准导航参数转移至模拟地区横向坐标系基准导航参数,其中姿态、速度基准量保持不变,位置基准计算所用公式为式(26),该模块需保留上一周期模拟地区的基准速度、基准位置,即式(20)和式(26),故需要一周期的记忆功能;IMU转换器为模拟测试核心模块,功能是将测试惯导IMU数据转换为模拟IMU数据,所用公式为式(12)和式(16),公式分析指出,相关变量的计算需要中低纬度基准姿态、速度、位置,以及模拟基准位置信息;极区导航计算机根据初始模拟位置信息和模拟IMU数据运行极区横向坐标系编排的惯导解算程序;轨迹标绘器通过极区导航计算机的位置解算绘制轨迹;误差分析器通过比较模拟地区基准导航参数与极区导航计算机解算参数,进行后续分析。
3 仿真试验
3.1 中低纬度基准轨迹设置与导航参数坐标转换仿真分析
采用轨迹发生器,在中低纬度生成一段轨迹,总时长48 h。轨迹特征如下:起点为地理坐标系下(10°N,0°),静止起步匀加速25 s至5 m/s,运行过程中速度大小不变,航向角初始为地理系下北偏东30°,在第6 h、第18 h左转弯,第30 h、第42 h右转弯,转弯时设置载体倾斜以模拟实际情况,48 h后减速到0。以轨迹发生器生成的无误差导航参数作为基准,绘制基准的轨迹、速度、姿态在横向坐标系下的投影结果,如图4~图6。

图4 横向坐标系下中低纬度基准轨迹Fig.4 Reference trajectory at middle and low latitudes of transverse coordinate system

图5 横向坐标系下中低纬度基准姿态Fig.5 Reference attitude at middle and low latitudes of transverse coordinate system

图6 横向坐标系下中低纬度基准速度Fig.6 Reference velocity at middle and low latitudes of transverse coordinate system
轨迹起点为0°经线,恰为横向坐标系赤道,10°N对应横向经度80°,起初向地理东北(横向西北)方向运行。经分析图4符合预期,可见位置基准坐标转换正确。
横纵摇、横横摇与纵摇、横摇相等;航向角起初为地理系下北偏东30°,而横向北方向为地理东方向,因此在横向系为60°,其后载体每左转一次航向角加90°,每右转一次航向角减90°。据图5可知,姿态基准转换符合预测。
轨迹第一段速度为横向北5·sin 30°=2.5 m/s,横向西5·cos 30°≈4.33 m/s,此后每次转向时横航向角变化,速度方向也随之变化,但其大小保持5 m/s,由图6计算可知,速度基准转换符合推测结果。
3.2 极区模拟测试仿真试验

将中低纬度测试惯导IMU转化为极区模拟IMU输出,进行模拟测试,结果如图7~图13。图7和图8绘制了模拟测试轨迹及其误差。图9和图10分别绘制了模拟IMU解算速度及速度误差。图11~图13分别绘制了模拟IMU解算横纵摇、横横摇及其误差和航向角误差。
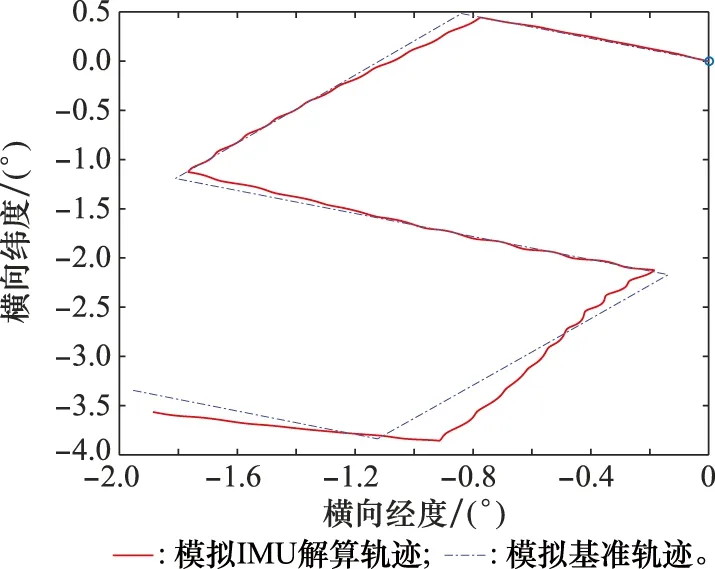
图7 极区模拟基准轨迹与解算轨迹Fig.7 Reference trajectory and calculated trajectory of polar simulation

图8 极区模拟测试位置误差Fig.8 Position error of polar simulation test

图9 极区模拟测试速度Fig.9 Velocity of polar simulation test
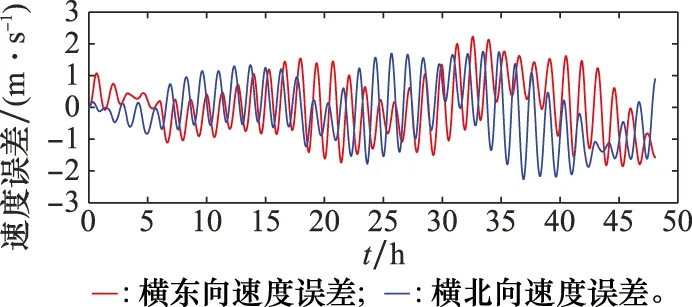
图10 极区模拟测试速度误差Fig.10 Velocity error of polar simulation test

图11 极区模拟测试水平姿态角Fig.11 Horizontal attitude angle of polar simulation test

图12 极区模拟测试水平姿态角误差Fig.12 Horizontal attitude angle error of polar simulation test

图13 极区模拟测试航向角误差Fig.13 Heading angle error of polar simulation test
3.3 极区模拟测试仿真试验误差分析
在设置仿真条件(陀螺漂移0.01°/h等)与不计基准误差的条件下:极区模拟测试的横向经纬度误差含有舒拉周期振荡成分,并被傅科周期振荡调制,误差逐渐发散,24 h内最大定位误差小于5 n mile,48 h最大定位误差约为15 n mile;速度、水平姿态误差也为舒拉振荡形式,与极区惯导解算的普遍表现相同,速度误差最大值约为2 m/s,横横摇、横纵摇误差最大值约为40~50角秒;横航向角误差线性发散,48 h误差发散到约28角分。
根据文献[18]的极区横向编排误差分析,陀螺漂移会造成横经纬度、横航向误差发散,也与模拟测试解算相符;文献[18]设置元件误差与本文相同,比较模拟测试误差与所述文献中极区动基座仿真试验误差,各个导航参数误差表现形式及量级基本一致。
3.4 仿真试验结论
根据中低纬度基准图像分析得出结论,地理坐标系与横向地理坐标系之间导航参数转换正确;根据模拟测试仿真试验结果初步分析得出结论,模拟测试IMU转换公式推导、模拟测试基准转换、横向坐标系编排下的惯导解算均正确;根据误差分析得出结论,在基准误差远低于测试惯导误差的条件下,同一惯导系统极区模拟测试误差与极区实地运行误差相当。
4 结 论
本文针对极区惯性导航设备的试验问题,探究了中低纬度模拟极区测试的方法,以避免地球曲率的影响造成轨迹二次投影为切入点,提出了轨迹转移过程中横向坐标系下速度、姿态不变的原则,在理论上详细推导了基准转换过程和IMU转换过程。对基准的不同情况进行分类,并提出了以高精度INS/GNSS组合导航为基准的具体测试方案。仿真试验验证了模拟测试算法理论的正确性,以及在基准误差不计的条件下,模拟测试误差与极区横向编排解算误差相当,为简化模拟测试体系误差分析奠定了基础。

