Leg-by-leg机动条件下纯方位跟踪的观测站机动策略
奚 畅,蔡志明,袁 骏
(海军工程大学电子工程学院,湖北 武汉 430000)
0 引 言
纯方位目标被动跟踪又称纯方位目标运动分析,指利用被动观测的目标方位信息估计目标运动参数的过程。由于方位信息是目标运动参数的不完全描述,目标可观测的必要非充分条件是观测站进行机动。为了使可观测性尽量强,需选择合适的观测站机动策略,这关系到目标状态估计的收敛率、收敛速度、估计精度、滤波稳定性等性能。
Fisher信息矩阵(Fisher information matrix,FIM)是一次观测所能提供的关于未知多维参数的信息量期望值的一种度量,是计算目标状态估计误差Cramer-Rao下界(Cramer-Rao lower bound,CRLB)、几何定位散布精度(geometric dilution of precision,GDOP)等指标的基础。由于FIM刻画了估计系统理论上最佳可达性能,以FIM行列式最大作为最优机动策略的性能指标是主流的研究方向[1-4]。基于FIM的机动策略设计方法需要在观测站机动前计算各种机动方案对应的观测过程中累积的FIM,而FIM计算所需的目标距离信息在机动前未知,对此问题的解决方法分为两类。
第一类方法是边估计运动参数-边优化观测站轨迹,即利用最新估计的目标距离计算FIM,得到局部最优机动策略。Liu[1]用最优控制论中的Hamilton-Jacobi方程求解观测平台的最优轨迹,得到对目标的追击曲线。Hammel[2]在拖线阵航向变化小于20次的限制条件下,提出最优轨迹的近似数值解法。文献[5]给出了位变率最大指标下的机动策略,并分析了目标各种运动情况下的最优轨线特性。文献[6]基于FIM行列式最大指标和方位变化率最大指标,结合贪心算法提出“一步最优”的机动轨迹。应用变分法和极值原理,文献[7]得到Gram矩阵最大和FIM行列式增量最大两种指标条件下最优轨迹方程。当利用扩展卡尔曼滤波进行跟踪时,文献[8]根据CRLB递推公式[9],以CRLB最小(FIM行列式最大)为准则设计折线形的拖船机动轨迹。此类方法的缺陷在于观测站需要利用局部最优策略进行多次机动,在实际应用场景中难以实施。
第二类方法是基于观测站leg-by-leg机动模式,得到与目标方位相关的转向规则。Leg-by-leg机动是由两个匀速直行段组成的折线形机动,希望利用一次转向达到全局最优,是一种易于实施的机动模式。文献[10]假设leg-by-leg机动中的转向可瞬间完成,通过讨论若干情景下的可观测性问题,可提出系统可观测的必要条件。Le[11-13]采用多重线性代数的方法,利用两个直行段的目标方位变化率得到FIM行列式的近似值,证明观测者的最优机动策略应是在最大和最小位变率间跳变的bang-bang控制。Fawcett[14-15]假设目标距离较远,利用转向前后目标初始方位线及其垂线方向的相对速度变化近似计算FIM,认为观测站的最优转向角度应是初始方位的垂直方向。此类方法的缺陷在于只能得到与目标方位有关的某种转向规则,无法计算FIM的解析值。
在实际的目标运动分析场景下,希望通过一次观测站转向机动,以最短时间实现满足某种精度要求的目标运动状态估计,机动策略设计的关键在于观测站机动前计算完整观测过程中累积的FIM。为了在leg1段计算各机动方案的FIM,以便根据参数估计精度和估计时间的要求设计机动策略,一方面,对于匀速直线运动的目标,假设相对速度在x轴、y轴的分量与初始距离的比值已知,且目标速度范围已知,通过假设目标速度对目标初始状态进行粗估,提出了使归一化初始距离粗估误差最小的目标速度假设方法;另一方面,对FIM行列式进行近似及多项式展开,提出了通过控制前后leg段比例以减小状态粗估误差对FIM行列式的影响。
1 系统模型
对于含有角度测量的目标运动分析,笛卡尔坐标系下的目标状态估计存在方差发散和结果不稳定的现象。修正极坐标系[16]将状态向量中的可观测部分和不可观测部分解耦,在滤波过程中避免了病态方差矩阵,增加了滤波稳定性,其结果渐近无偏[17-19]。
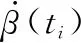
(1)

设ax(ti)、ay(ti)分别为目标相对观测站在x轴、y轴方向的加速度,以初始时刻目标和观测站的状态为基准,相对加速度导致的相对速度及相对位置变化为
(2)
式中:w1(ti)和w2(ti)分别表示x轴、y轴方向的相对速度变化;w3(ti)和w4(ti)分别表示x轴、y轴方向的相对位置变化。设VR(ti)和VB(ti)分别为目标初始方位方向、目标初始方位垂直方向上的相对速度变化,AR(ti)和AB(ti)分别为目标初始方位方向、目标初始方位垂直方向上的相对位置变化,则有
(3)
定义中间变量:
(4)
将目标状态向量y(ti)表示为初始时刻目标状态向量y(t0)的函数,可得修正极坐标系下[16]的状态方程:
(5)
纯方位测量情况下,观测量是目标状态向量中的元素,测量方程可表示为线性形式:
(6)
式中:η(ti)表示量测噪声,服从均值为0、方差为R的独立高斯分布。
2 Leg-by-leg机动模式下的FIM计算
Leg-by-leg机动由两个运动方向不同的匀速直行段组成,又称转向机动、折线机动、两段直航式机动,是一种易于实施的机动模式,适用于船艇等机动性欠佳的观测载体。按照时间先后顺序,两个匀速直行段分别称为leg1段和leg2段。实际场景下,观测站在搜索目标时的工况是匀速直线运动,发现目标后希望尽快确定其位置,因此通常将发现目标的时刻作为leg1段的起始时刻。
假设目标保持匀速直线运动,观测站进行leg-by-leg机动,转向时刻为ta且瞬时完成转向,leg2段结束时刻为tk,则相对加速度由观测站转向产生,用ar、ab分别表示目标初始方位方向、目标初始方位垂直方向上转向前后的观测站速度变化,则有
(7)
(8)
(9)
(10)
将式(4)代入式(5)可得ti时刻的目标方位值:
(11)
由定义可得对初始时刻目标状态的FIM:
(12)
式中:i为采样序号,Ji(y0)为雅克比矩阵:
(13)
(14)
对于leg-by-leg机动模式,在笛卡尔坐标系下用传统方法计算FIM[20-21]需利用各采样时刻的目标距离值和方位值,在转向之前无法获得转向后的相关参数,因而无法对转向策略提出指导。假设转向可瞬时完成,在修正极坐标系下计算FIM只需初始时刻的目标状态和观测站转向前后的速度变化量,可在转向前计算各机动方案对应的观测过程中累积的FIM,进而根据参数估计精度和估计时间的要求设计合适的机动策略。
3 目标初始状态粗估
3.1 初始状态粗估方法

(15)
设vo为观测站速度,vox、voy分别为观测站速度在x轴和y轴的分量,θ为目标航向,vt为目标速度,vtx、vty分别为目标速度在x轴和y轴的分量,vrx/r0、vry/r0可写为
(16)
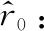
(17)
3.2 目标速度假设方法
假设可以准确测量目标方位测量并估计vrx/r0、vry/r0,初始时刻目标状态向量中只有距离的估计存在误差,目标速度的假设对于初始距离估计误差起关键作用。根据式(17)可得初始距离粗估误差:
(18)
由式(18)可知,初始距离粗估误差与目标真实初始距离成正比,与相对运动速度成反比,与初始距离粗估误差正相关。对于目标真实速度较小的情况与目标真实速度较大的情况,相同的目标速度假设误差造成的影响不同,因此将目标速度假设为目标速度范围的中点无法得到统计意义上最小的初始距离粗估误差。
不失一般性,假设观测站航向为0°,对于目标假设速度为vt,h的情况,定义归一化的初始距离粗估误差为
(19)
对于目标速度和运动方向满足一定概率分布的情况,目标速度假设值vt,h应使g(vt,θ)的期望最小。
由式(17)可知,目标速度假设值vt,h需满足
(20)
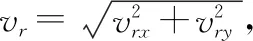
(21)
即目标速度假设值vt,h应不小于观测站速度在相对运动垂直方向的分量。
根据目标类型和跟踪场景,可知目标的速度范围为[vt,min,vt,max]。如果目标最小速度vt,min大于等于观测站速度vo,目标速度假设值vt,h在[vt,min,vt,max]范围内取值可保证式(21)成立。假设目标速度vt服从[vt,min,vt,max]范围内的均匀分布,目标运动方向θ服从[0,360°)范围内的均匀分布,vt和θ的概率密度函数分别为
(22)
由于变量vt和θ彼此独立,可得联合概率密度函数:
(23)
在[vt,min,vt,max]范围内按固定间隔取若干离散值,依次将所取值作为目标速度假设值vt,h,计算归一化距离粗估误差的期望:
(24)
选择使归一化距离粗估误差期望最小的目标速度假设值,代入式(17)完成初始距离粗估。
如果目标最小速度vt,min小于观测站速度vo,目标速度假设值vt,h须在[voxvry/r0-voyvrx/r0,vt,max]范围内取值以满足式(21)成立,voxvry/r0-voyvrx/r0即为目标速度假设下限。由于目标速度假设下限与观测站速度和相对速度方向相关,无法解析地计算归一化距离粗估误差的期望,需要对于各种目标速度假设下限的情况,分别通过蒙特卡罗仿真计算归一化距离粗估误差期望随目标速度假设值变化情况。目标运动分析过程中,利用估计的vrx/r0、vry/r0计算目标速度假设下限,选择此情况下使误差期望最小的目标速度假设值,代入式(17)完成初始距离粗估。
4 减小距离粗估误差影响
第3节致力于减小初始距离粗估误差,本节将讨论如何减小误差对FIM行列式的影响。首先计算FIM行列式的解析表达式,式(11)~式(14)较为复杂无法展开,需对其进行简化。利用反正切函数的泰勒级数,对式(11)进行一阶展开可得
(25)
式(25)对初始时刻状态向量求偏导,可得雅克比矩阵中的元素,如下所示:
(26)
利用分式的泰勒级数,对式(26)进行一阶展开得到
(27)
(28)
--------------------
设采样间隔为Δt,将式(12)中的求和变为积分的形式:
(29)
对于两个积分区间,将式(9)和式(10)代入式(28)得到雅克比矩阵Ji(y0),利用基于计算机代数系统的Mathematica软件对式(29)进行积分运算,得到的FIM行列式是一个包含2 460个分项的多项式,初始距离r0以其倒数s0=1/r0的形式在式中体现。多项式各项中s0的阶数从0阶到10阶不等,以s0的阶数作为索引,将FIM行列式表示为
(30)
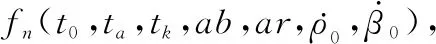
(31)
式中:tk-ta表示leg2段的时长。因此leg2段时间越短,高阶s0项对结果影响越小,初始距离粗估值对FIM行列式的影响越小。用Ra=(ta-t0)/(tk-t0)∈[0,1]表示leg1段占leg-by-leg机动总时长的比例,leg-by-leg机动总时长一定时,增大Ra可减小初始距离粗估误差的影响。但是,Ra=1表示观测站匀速直行未发生机动,Ra接近1会造成真实的|FIM(y0)|较小,不利于目标参数估计。

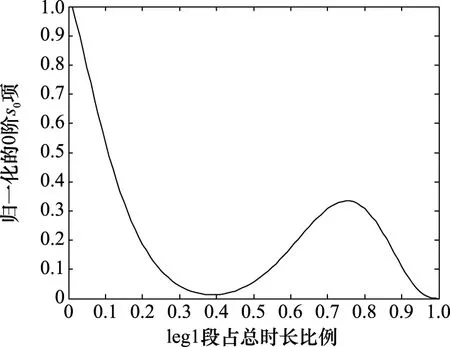
图1 归一化的0阶s0项变化情况Fig.1 Change of normalized zero-order term of s0
由图1可知,Ra处于[0.7,0.8]范围内时归一化的0阶s0项相对较大。因此,leg-by-leg机动总时长一定时,应对于[0.7,0.8]范围内的各种Ra和[0,360°)范围内的各种观测站转向角度计算FIM行列式,根据参数估计精度和估计时间的要求设计最优机动策略。
5 实验与结果分析
5.1 目标速度假设方法
在水下目标跟踪场景下进行讨论,假设观测站速度为4 kn,观测站运动方向为0°,目标速度服从[5,10]kn范围内的均匀分布,目标运动方向服从[0,360°)范围内的均匀分布。由于观测站速度小于目标最小速度,目标速度假设值vt,h可以在[5,10]kn范围内取值,对于[5,10]kn范围内间隔0.2 kn变化的若干种目标速度假设情况,依次利用式(24)计算归一化距离粗估误差期望的理论值,利用106次蒙特卡罗仿真计算归一化距离粗估误差期望的仿真值,结果如图2所示。
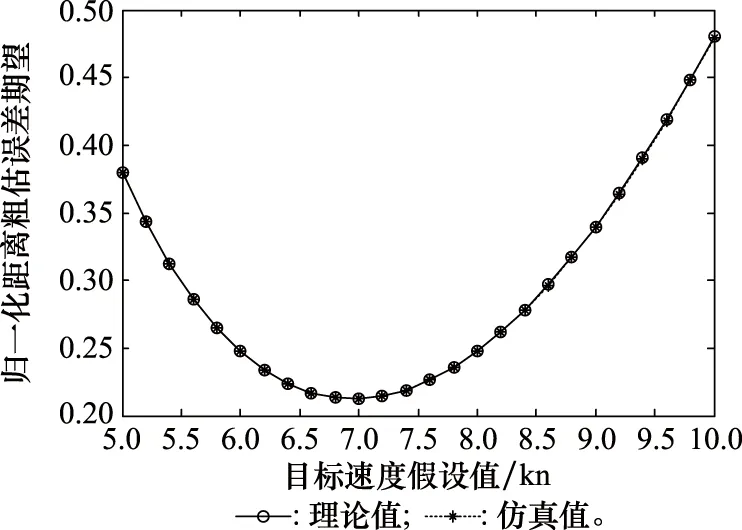
图2 归一化距离粗估误差(目标速度假设下限固定)Fig.2 Normalized distance rough estimation error (lower bound of target velocity assumption is fixed)
由图2可知,目标速度假设值为7 kn时归一化距离粗估误差期望达到最小,对于上述假设的目标速度和目标速度范围,应令目标距离假设值为7 kn。归一化距离粗估误差期望的理论值和蒙特卡罗仿真值基本一致,可认为两种方法等效,无法解析计算粗估误差期望时采用蒙特卡罗仿真方法进行替代是合理的。
假设观测站速度为4 kn,观测站运动方向为0°,目标速度服从[0,10]kn范围内的均匀分布,目标运动方向服从[0,360°)范围内的均匀分布。由于观测站速度大于目标最小速度,需要对于各种可能的目标速度假设下限,分别计算使归一化距离粗估误差期望最小的目标速度假设值。间隔1 kn设置若干种目标速度假设下限情况,通过106次蒙特卡罗仿真计算各种目标速度假设下限情况下,归一化距离粗估误差期望随目标速度假设值的变化,结果如图3所示。
目标运动分析过程中,可根据实际计算的目标速度假设下限,利用图3选择使误差平均值最小的目标速度假设值。例如,图3中目标速度假设下限为1 kn情况下,目标速度假设值等于1.2 kn时归一化距离粗估误差期望最小,因此如果在实际应用场景下计算的目标速度假设下限接近1 kn,应令目标速度假设值为1.2 kn。为方便绘图显示及说明,上述仿真以1 kn间隔设置目标速度假设下限情况,在实际应用中可以采用更小的间隔以获得更精确的结果。
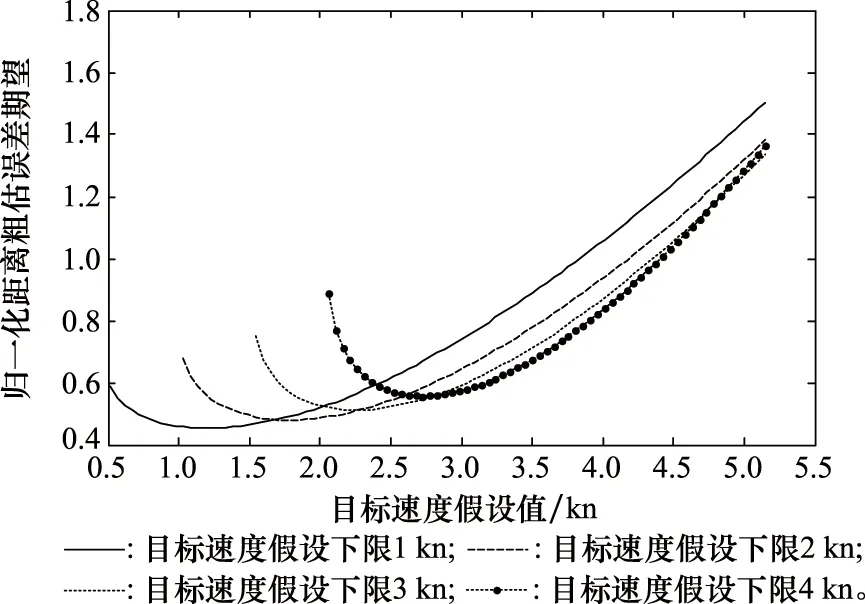
图3 归一化距离粗估误差(目标速度假设下限不固定)Fig.3 Normalized distance rough estimation error (lower bound of target velocity assumption is not fixed)
由图2和图3可知,观测站速度为4 kn,目标速度在[0,10]kn范围内时,利用第3节方法的归一化距离粗估误差期望小于0.6。
5.2 leg比例对FIM的影响
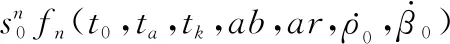

图4 各阶s0项变化情况Fig.4 Change of every order term of s0
由图4可知,s0阶数小于等于2的项显著大于其他项,FIM行列式主要由此3项决定。随着Ra增大,s0阶数大于0的项在Ra>0.3后逐渐收敛至0,s0阶数为0的项在Ra∈[0.7,0.8]时达到极大值,与图1结论一致。
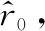
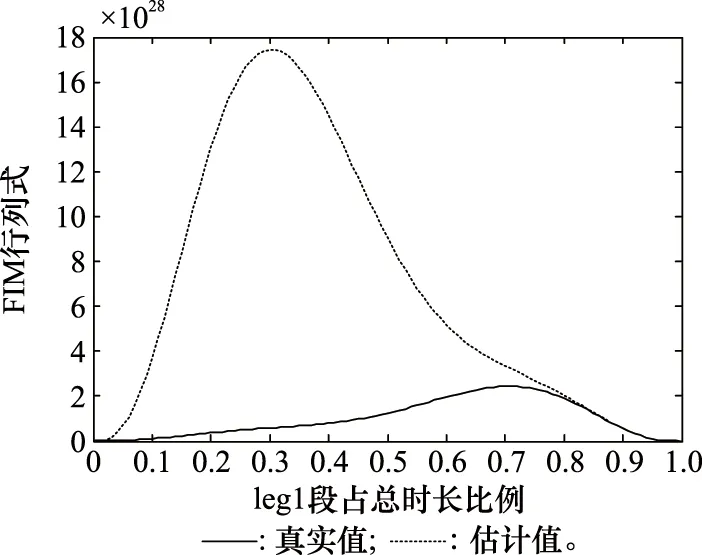
图5 FIM行列式随Ra变化情况Fig.5 Change of FIM determinant with Ra
由图5可知,Ra越大,FIM行列式的估计值越接近真实值,表示FIM行列式受目标粗估误差影响越小,Ra接近1时真实值与估计值基本吻合但FIM行列式接近0,与理论分析结果一致。
5.3 FIM估计精度验证
设观测站速度为6 kn,leg1段观测站航向为0°,目标初始方位为-30°,目标初始距离为10 km,目标速度为4 kn,目标航向为120°,leg-by-leg机动总时长为600 s,leg1段占总时长的比例Ra=0.8,方位测量方差为(0.5°)2,测量间隔为10 s。认为目标速度范围为[0,10]kn,对于不同的转向角度即leg2段运动方向,利用真实目标初始距离计算FIM行列式真实值,用目标初始距离粗估值计算FIM行列式估计值,结果如图6所示。
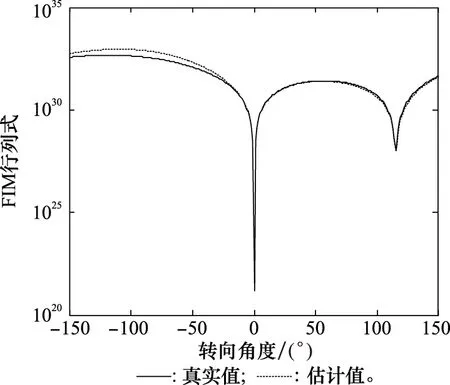
图6 FIM行列式随转向角度变化情况Fig.6 Change of FIM determinant with steering angle
利用FIM行列式真实值和估计值可得FIM行列式估计误差,除以FIM行列式真实值可得相对估计误差,将相对估计误差在转向角度维度取平均得到FIM行列式相对估计误差均值。对图6所示结果进一步处理可得,该机动场景假设下FIM行列式相对估计误差均值为0.37。
假设一种典型的水下目标跟踪场景,设观测站速度为6 kn,leg1段观测站航向为0°,leg-by-leg机动总时长为600 s,测量间隔为10 s,方位测量方差为(0.5°)2。目标初始方位范围为[0,360°),目标初始距离范围为[10,50]km,目标速度范围为[0,10]kn,目标航向范围为[0,360°),leg1段占总时长的比例Ra范围为[0.7,0.8],上述目标运动参数在各自范围内服从均匀分布。进行103次蒙特卡罗仿真,每次仿真时目标运动参数随机取值,利用与图6相同的方法计算FIM行列式相对估计误差均值,得到一次蒙特卡罗仿真的结果,将103次蒙特卡罗仿真的结果由小到大排序,如图7所示。由于初始距离粗估误差与相对运动速度成反比,相对运动速度极小时距离粗估误差极大,导致相对估计误差出现极大值。由图7分析可知,若以FIM行列式相对估计误差小于0.2作为有效估计准则,则有效估计概率为76.7%,有效估计情况下平均的相对估计误差为0.12。因此,认为在典型的水下目标跟踪场景下,利用本文方法可以较为有效地计算FIM,进而实现机动策略设计。
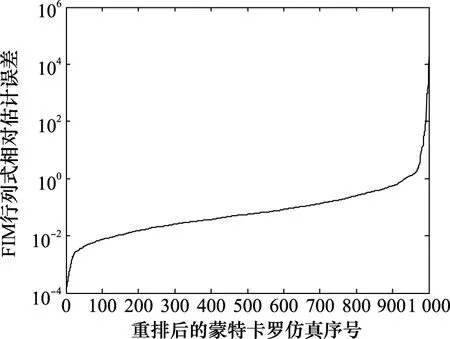
图7 FIM行列式相对估计误差Fig.7 Relative estimation error of FIM determinant
6 结 论
对于观测站leg-by-leg机动模式,为了在leg1段计算各机动方案的FIM,进而根据参数估计精度和估计时间的要求设计机动策略,从粗估目标初始距离和减小粗估误差对FIM行列式影响两方面着手开展研究。一方面,对于匀速直线运动的目标,假设相对速度在x轴、y轴的分量与初始距离的比值已知且目标速度范围已知,通过假设目标速度实现目标初始状态粗估,提出了使归一化初始距离粗估误差最小的目标速度假设方法;另一方面,对FIM行列式进行近似及多项式展开,提出了通过控制前后leg段比例以减小状态粗估误差对FIM行列式的影响。仿真结果表明:
(1)计算目标速度假设值时,解析方法和蒙特卡罗仿真方法等效,观测站速度为4 kn,目标速度在[0,10]kn范围内时,归一化距离粗估误差期望小于0.6;
(2)leg1段占总时长的比例在[0.7,0.8]范围内时,FIM行列式受目标初始距离粗估误差影响较小,且避免真实的FIM行列式趋近于0;
(3)对于典型的水下目标跟踪场景,FIM行列式的有效估计概率为76.7%,平均的相对估计误差为0.12,可有效地设计观测站机动策略。
本文方法的缺陷在于需要利用相对速度在x轴、y轴的分量与初始距离比值。后续研究内容包括:非瞬时转向情况下转弯半径对于FIM计算结果的影响;如何更准确地粗估目标初始状态;相对速度在x轴、y轴的分量与初始距离比值的估计误差对FIM计算结果的影响。

