基于单快拍空间平滑的多伯努利DOA跟踪算法
吴孙勇,邹宝红,薛秋条,孙希延,王 力
(1.桂林电子科技大学数学与计算科学学院,广西 桂林 541004;2.广西信息科学实验中心,广西 桂林 541004)
0 引 言
阵列信号处理技术广泛应用于移动定位、电子侦察、雷达跟踪、声呐系统等领域,而波达方向(direction of arrival,DOA)估计问题是阵列信号处理中的重点研究内容之一。经典的DOA参数估计算法一般都属于静态信号源的DOA估计,如基于波束形成的DOA估计算法[1]、多重信号分类[2-4]、旋转不变子空间技术[5]等算法。然而在实际场景中,信号源通常是运动的,采用该类算法进行DOA估计需要用多快拍批处理方式对接收矩阵进行处理,计算量大,无法满足DOA的动态实时跟踪。
目前,关于动态 DOA跟踪类算法的研究方法主要包括基于子空间类方法和基于状态滤波类方法。基于子空间类的跟踪算法[6-9],如投影近似子空间跟踪(projection approximation subspace tracking,PAST)算法[6-7]、紧缩PAST(PAST deflation,PASTD)算法[8]、双迭代奇异值分解算法[9]等,此类算法都是通过构造代价函数采用递归最小二乘法进行子空间更新,从而实现DOA跟踪。但是由于这类算法都考虑了一个固定的DOA数目场景,无法实现跟踪数目时变的DOA信号,且跟踪快速运动目标时性能下降。而状态滤波类方法采用基于贝叶斯框架下的粒子滤波算法递归估计动态系统的状态,被广泛的应用到DOA跟踪问题[10-13]。文献[10]提出一种基于改进粒子滤波算法的阵列单通道机动目标DOA跟踪方法,文献[11]提出单机动目标DOA跟踪粒子滤波算法,将多重信号分类(multiple signal classification,MUSIC)空间谱代替粒子滤波的似然函数,结果表明基于粒子滤波的跟踪算法优于传统的子空间类跟踪算法。但该类算法也无法实现跟踪信号源数目时变的DOA。
实际情况中,跟踪的信号源数目可能是时变的,如潜艇跟踪、移动定位等。Mathler提出的有限集统计学理论(finite set statistics theory,FISST)的概念,将多目标的状态和量测建模为随机有限集(random finite set,RFS),构建贝叶斯框架下的RFS滤波算法[14-16],为目标数目时变的跟踪问题提供了一种新的思路。目前,RFS滤波器的两个成熟分支是概率假设密度(probability hypothesis density,PHD)、势PHD(cardinalized PHD,CPHD)和多伯努利滤波器。由于这些理论中所得量测的前提假设是任何量测都是由最多单个目标产生,而阵列信号的量测不符合随机有限集理论下的“标准量测”。针对这个问题学者们提出多种方法解决[17-19],文献[17]提出了一种基于相控阵观测的多目标DOA跟踪的检测前跟踪滤波器,采用一个新的标记泊松点过程(marked poisson point process,MPP)模型并推导出MPP-PHD滤波器DOA跟踪的递归公式。文献[18]推导了具有高斯噪声的叠加传感器的PHD和CPHD滤波器的可近似处理计算。文献[19]提出一种适用于脉冲噪声的多元扩展目标的近似CPHD滤波器DOA跟踪算法。文献[20]基于随机有限集框架提出基于协方差的多目标DOA跟踪问题方法,该方法允许接收阵列量测直接进入CPHD滤波器中,用一个复杂的Wishart随机矩阵表示其似然分布,从而跟踪未知时变DOA。其中PHD、CPHD粒子滤波器传递后验分布的一阶矩和势分布,与PHD、CPHD粒子滤波器相比,多目标多伯努利(multi-target multi-Bernoulli,MeMBer)滤波器[21-28]将每个目标建模为伯努利RFS,并传递服从多伯努利分布的近似后验多目标密度参数,且在一段时间内维持许多伯努利分量,每个分量都是一个潜在的目标,使得MeMBer滤波器能更有效地对时变多目标进行跟踪。Choppala[24]等人提出将 MUSIC 谱函数作为MeMBer的伪似然函数,对相控阵列进行有效的DOA 跟踪。在文献[25]中研究了在监控中随机出现或消失的单一运动源的联合检测和DOA跟踪问题,提出了一种用于跟踪随机开/关的单动态系统的检测前跟踪伯努利滤波器。文献[27]提出一种基于无迹变换MeMBer滤波框架下的多源到达方向跟踪算法。这类多伯努利DOA跟踪算法中,每个时刻都需要多快拍数据构造较为精准的阵列协方差矩阵的估计阵,再采用MUSIC伪似然函数直接对传感器信号进行滤波。实际应用中我们难以在瞬时间内获得多个平稳独立的快拍数据。
针对以上问题,本文提出了一种新的单快拍情况下粒子滤波类的跟踪算法—基于空间平滑的MeMBer(spatial smoothing with MeMBer,SS-MeMBer)跟踪算法。由于每时刻获取的单快拍数据难以直接应用到多伯努利滤波器中计算量测似然函数,因此本文利用空间平滑方法对量测进行处理,用平滑后的数据代替协方差矩阵,进行奇异值分解,用MUSIC空间谱函数作为多伯努利的伪似然函数。该算法首先建立均匀线阵的量测模型,并以目标运动模型作为状态模型对目标状态和数目进行预测。然后,在更新阶段利用平滑后的数据代替协方差矩阵,进行奇异值分解,构造噪声子空间,用MUSIC空间谱函数作为多伯努利的伪似然函数,最后根据多伯努利滤波器理论对目标状态进行递归跟踪,并进行状态提取。该算法的主要优点是在每时刻获取到的单快拍量测信息时,可以准确跟踪信号源数目时变和状态未知的DOA。
1 问题描述
1.1 随机有限集理论
假设k时刻单个目标状态为xk,则状态转移模型和量测模型分别为
(1)
式中:fk,hk分别表示状态转移函数和量测函数;nk,wk分别表示为过程噪声和量测噪声。
在k时刻有Mk个目标xk,1,xk,2,…,xk,Mk(xk,i∈Rnx)和Nk个量测zk,1,zk,2,…,zk,Nk(zk,i∈Rnz),其中nx,nz分别表示状态和量测的维度。把k时刻目标状态和量测的有限集分别表示为
(2)
根据状态空间F(X)和量测空间F(Z)可以建立多目标贝叶斯滤波器。假设πk(·|Z1:k)表示k时刻的多目标后验密度,根据文献[22]随时间贝叶斯递归传播多目标后验密度为
πk|k-1(Xk|Z1:k-1)=
(3)
πk(Xk|Z1:k)=
(4)
式中:积分项为RFS变量X的FISST集积分;πk|k-1(·|·)为多目标的后验概率密度函数;fk|k-1(·|·)表示多目标转移概率;gk(·|·)是多目标似然函数。
1.2 多伯努利滤波器
(5)
根据贝叶斯理论,MeMBer滤波器估计目标状态分为预测和更新两个阶段,其中预测过程为
(6)

且k时刻多伯努利随机有限集更新为
(7)
式中:
(8)
(9)

1.3 阵列模型
考虑由M个全向阵元组成的等距线阵,阵元间距为d≤λ/2(λ是入射信号波长),现有K个远场窄带信源分别以角度θi(i=1,2,…,K)入射接收线阵。以阵元1为参考阵元,则第m个阵元的输出信号可表示为
(10)
式中:si(t)为第i个信号的复包络;nm(t)为第m个阵元接收到的理想高斯白噪声。
则阵列接收的数据可进一步表示为
Y(t)=[y1(t),y2(t),…,yM(t)]T=A(θ)S(t)+N(t)
(11)
式中:A(θ)=[a(θ1),a(θ2),…,a(θK)]为M×K维阵列流形矩阵;a(θi)=[1,e-j2πdsinθi/λ,…,e-j2πd(M-1)sinθi/λ]为第i个信源方向矢量,阵列高斯白噪声矢量为N(t)=[n1(t),n2(t),…,nM(t)]T,且满足:
(12)
假设信号与噪声不相关,接收阵列的协方差矩阵为
R=E[Y(t)YH(t)]=A(θ)RSA(θ)H+RN
(13)

(14)
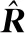
2 空间平滑多伯努利DOA跟踪算法
本节通过在传感器阵列中采样单快拍量测数据,针对时变DOA跟踪问题,给出SS-MeMBer DOA跟踪算法理论。

(15)
式中:vk为高斯白噪声;Fk是状态转移矩阵。
假设在k时刻M个全向阵元接收的阵列信号为,则传感器量测模型为
Yk=[y1(k),y2(k),…,yM(k)]T=A(θ)S(k)+N(k)
(16)
式中:A(θ)=[a(θ1),a(θ2),…a(θK)]为M×K维阵列流形矩阵;S(k)表示入射信号强度;N(k)=[n1(k),n2(k),…,nM(k)]T为阵列高斯白噪声矢量。

(17)
式中:
(18)
(19)

(20)

(21)
后向平滑数据为
(22)
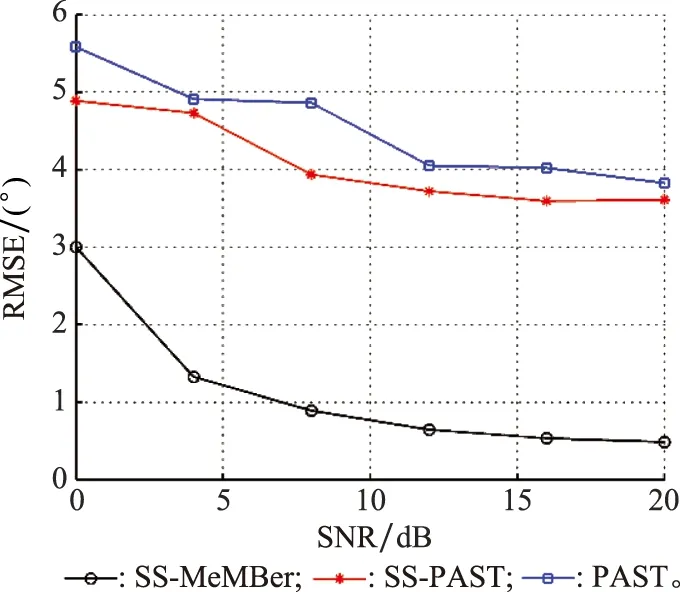
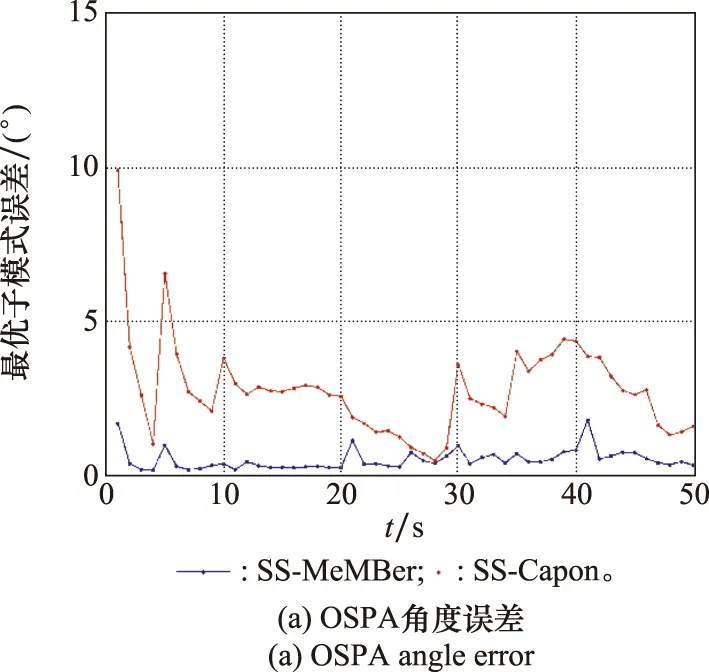
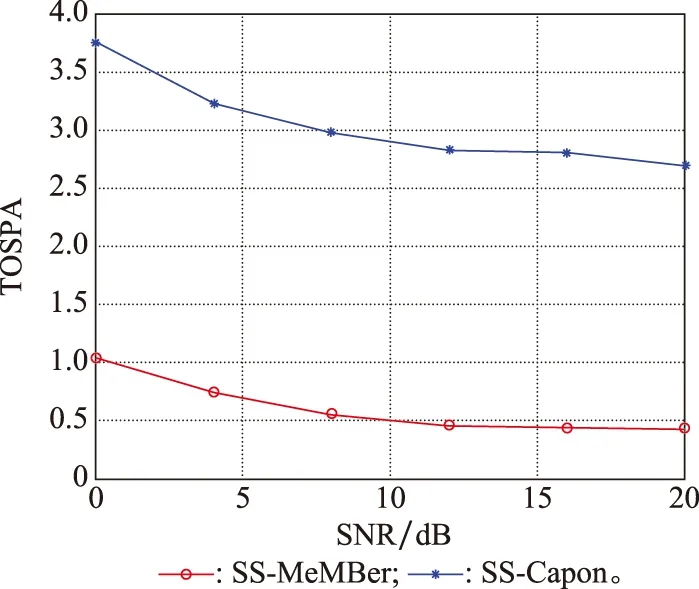
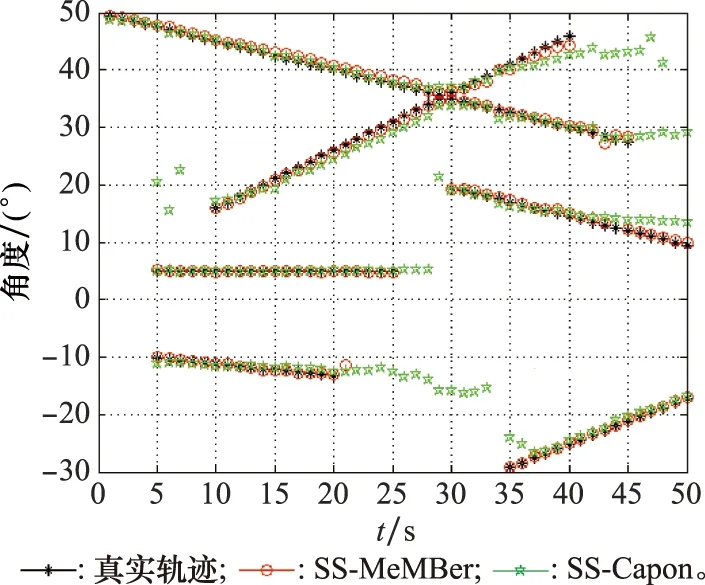
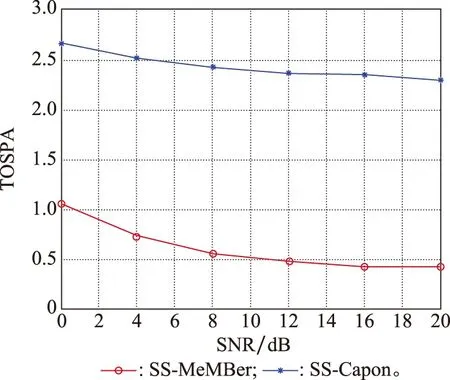
式中:K为信源个数;l是平滑子阵阵元个数,1≤l 则平滑后的数据为 (23) (24) (25) (26) 因此,多伯努利滤波器更新阶段参数集分别为 (27) (28) (29) 权重为 (30) 式中:ps表示存活的概率;fk|k-1表示存活粒子的状态转移函数;pb表示新生粒子的概率;B表示从建议概率βk中新生的粒子数;与βk相对应的概率密度bk|k-1采用均匀分布模型。 k时刻多目标多伯努利粒子滤波更新阶段的后验概率密度可以表示为 (31) 权重为 (32) 式中:通过所得的噪声子空间与监测区域任何估计目标的粒子状态得到MUSIC-伪似然函数为 (33) 多伯努利后验p(xk|Y1:k)可将式(33)代入式(28)中可得,已知离目标越近的粒子权重就越大,最后通过重采样选取权重大的粒子,消除权重小的粒子。算法流程如下所示。 下列仿真实验中,检验算法优劣性的指标之一是均方根误差(root mean square error,RMSE),是指预测值与真实值偏差的平方与观测次数n比值的平方根,衡量观测值与真实值的偏差。其定义分别为 (34) (35) 此外,本文还选择一个度量标准,即最优子模式分配(optimal subpattern assignment,OSPA)误差[18]。其不仅计算估计角度和真实角度之间的误差,而且还可以量化当存在的信源被忽略或不存在的信源被错误地检测到时的惩罚,常用来评估多目标滤波问题的性能。OSPA误差定义为 (36) d(c)(x,y)=min(c,d(x,y)) (37) 式中:d(x,y)=‖x-y‖表示x和y间的距离,x,y分别表示真实值和估计值;集合X={x1,x2,…,xm}和Y={y1,y2,…,yn},m、n分别表示真实值个数和估计值个数;c表示惩罚参数;p表示阶数参数;Πn代表从集合{1,2,…,n}中取出m个元素进行排列的集合。 实验 1条件如下:时间步长ΔT=1 s,阵元个数M=10,信噪比(signal to noise ratio,SNR)为15 dB,观测时间T=100 s,信源数目为3,状态时变,数目保持不变,信源初始状态分别为x1(0)=[50,-0.15]T,x2(0)=[10,0.1]T,x3(0)=[-10,0]T,且接收量测为单快拍量测,信源存活概率为ps,k=0.98;在SS-MeMBer DOA跟踪算法的预测阶段,假设每个时刻有6个新生信源,即JB,k=6,是[-π/2,π/2]上的均匀分布,每一个新生源产生300个粒子,即NB,k=300。 图1是在SNR为15 dB的条件下,100次MC实验的轨迹跟踪效果图。图1(a)是轨迹跟踪图。图1(b)是运行100次MC实验的联合均方误差图。从图1可以看出跟踪3个目标时,当目标快速运动时,PAST及基于空间平滑的PAST(spatial smoothing with PAST,SS-PAST)算法由于每次快拍间的步长大,导致子空间跟踪性能下降。当目标运动缓慢或不变,3个算法跟踪性能基本一致。因此,本文提出的SS-MeMBer算法在跟踪快速运动目标时的估计值要比传统的PAST算法,SS-PAST算法[6]的估计值更接近真实值,RMSE更小。 图1 DOA跟踪的轨迹跟踪和RMSEFig.1 Trajectory tracking and RMSE of DOA tracking 图2为上述3种算法随着SNR的变化的联合RMSE。从图2可以看出3种算法的联合RMSE图都随SNR增加呈现下降趋势,SNR越大,RMSE越小。图2中可以明显看出,不同SNR下SS-MeMBer算法的RMSE小于SS-PAST算法和PAST算法。 图2 不同SNR下DOA跟踪的RMSEFig.2 RMSE of DOA tracking with different SNR 实验 2由于传统的DOA跟踪算法需要预先知道信源个数才能进行DOA跟踪,不能处理信源数目时变的跟踪问题。实验2是考虑信源数目时变,分析SS-MeMBer算法的性能。本文使用平滑后的数据得到的MUSIC空间谱函数作为多伯努利粒子滤波似然函数,提出了SS-MeMBer算法。选择基于Capon谱函数作为粒子似然函数的多伯努利粒子滤波(简称为SS-Capon)算法作为对比算法。其中SS-Capon算法的Capon谱伪似然函数为 (38) 由于Capon波束形成算法的最优性能是建立在采样快拍数足够多以及对目标信号导向矢量精确己知的前提之上,当快拍数较少时,Capon波束形成算法会产生高旁瓣的波束响应,从而使得算法性能下降。因此,采用在单快拍空间平滑条件下得到的伪协方差作为平滑后的量测数据进行协方差求逆运算得到Capon谱伪似然函数。 实验条件如下:阵元个数M=20,SNR为15 dB,观测时间T=50 s,考虑一个有6个信源的多源检测场景,其中信源状态与数目都是时变的,信源的出生死亡时间以及目标运动情况如表1所示。 表1 目标轨迹情况Table 1 Target trajectory condition 图3是在SNR为15 dB的条件下,6个目标一次MC的轨迹跟踪图,从图3中可以看出本文所提出的SS-MeMBer算法比SS-Capon算法更准确跟踪目标航迹,SS-MeMBer算法的估计值在真实角度附近波动,且在目标消失情况下能及时检测到目标消亡。而SS-Capon算法在相同的实验条件估计角度时出现漏估的情况,并且估计出的角度存在于真实状态有很大偏差的情况。因此,SS-MeMBer算法比SS-Capon算法跟踪信源更准确。 图3 轨迹跟踪图Fig.3 Diagram of trajectory tracking 运行100次MC时,为了更好地评估SS-MeMBer算法和MPP-PHD算法性能,选择OSPA误差度量,更直观评估多目标滤波跟踪问题的性能。图4是在SNR为15 dB条件下,SS-MeMBer 算法和SS-Capon算法的OSPA误差图和势误差比较图。图4(a)是OSPA角度误差图,其中阶数参数p=1,惩罚参数c=10°,从图4(a)中可看出SS-MeMBer算法的OSPA误差在目标出现的时刻明显增大,但整体上SS-MeMBer算法OSPA误差明显小于SS-Capon算法。图4(b)是运行100次MC的势分布估计图,从图4(b)中可看出当信源数目时变的时候,SS-MeMBer算法在目标出现或消失时都能够准确地估计信源数目,其势估计几乎能够与真实的信源个数重合,而SS-Capon算法从势估计图上看整体都低估了信源的势。通过100次实验结果显示,SS-MeMBer 算法比SS-Capon算法跟踪效果更好。 图4 RMSE和势估计图Fig.4 Diagram of RMSE and cardinality estimation 图5是SS-MeMBer 算法和SS-Capon算法在不同SNR下得到的估计值与真实值之间的TOSPA角度误差图,其中TOSPA表示在某一SNR下所有时刻的OSPA时间平均值。从图5中可以看出,SS-MeMBer 算法和SS-Capon算法在不同SNR的OSPA角度误差,并且都随着SNR增大而减小,但SS-MeMBer 算法的OSPA角度误差都比SS-Capon算法的OSPA角度误差小。综上,可以得出在多伯努利滤波器算法实现中采用MUSIC似然函数跟踪结果比采用Capon谱函数作为似然函数性能更优。 图5 不同SNR下的TOSPA误差图Fig.5 Diagram of TOSPA error with different SNR 本文所提出的SS-MeMBer算法,采用的是多伯努利粒子滤波器估计多目标后验密度,而PHD滤波是直接估计一阶矩来进行跟踪的,因此选择了与文献[14]提出的用于DOA跟踪的标记点泊松过程PHD(简称为MPP-PHD)滤波器作对比。 图6是在SNR为15 dB条件下,一次MC的轨迹跟踪图,从图6中可以看出,当信源存在时本文所提出的SS-MeMBer算法与MPP-PHD算法都能估计出信源真实航迹,但在信源消失情况下SS-MeMBer算法能及时检测到目标消亡。而MPP-PHD算法当目标消失时,不能及时估计目标消失,存在一定的延时。 图6 DOA轨迹跟踪图Fig.6 Trajectory of DOA tracking 图7是在SNR为15 dB,目标数目为6,MC=100时,SS-MeMBer 算法和MPP-PHD算法的OSPA误差图和势误差比较图。图7(a)是OSPA角度误差图,其中阶数参数p=1,惩罚参数c=10°,从图7(a)中可看出SS-MeMBer算法的OSPA误差在目标出现的时刻明显增大,但整体上SS-MeMBer算法OSPA误差明显小于MPP-PHD算法。图7(b)是运行100次MC的势分布估计图,从图7(b)中可看出当信源数目时变的时候,SS-MeMBer算法估计的势基本与真实的势相一致,并且当数目发生变化是也能够准确的估计信源数目,而MPP-PHD算法对于数目发生变化时不能及时估计时变信源的势。 图7 DOA跟踪RMSE和势估计图Fig.7 RMSE of DOA tracking and cardinality estimation 图8是SS-MeMBer 算法和MPP-PHD算法在不同SNR条件下的估计值与真实值的TOSPA角度误差图,从图8中可以看出SS-MeMBer 算法和MPP-PHD算法的OSPA角度误差都随着SNR增大而减小,但整体SS-MeMBer 算法的OSPA角度误差都比MPP-PHD算法的OSPA角度误差小。 图8 不同SNR的DOA跟踪TOSPA误差图Fig.8 TOSPA of DOA tracking with different SNR 本文提出了基于空间平滑的多伯努利滤波器DOA跟踪算法。该算法直接采用传感器阵列所得的单快拍数据进入多伯努利滤波中并在更新阶段使用空间平滑进行处理,用平滑后的数据构成的矩阵代替协方差矩阵估计阵,生成MUSIC谱函数作为多伯努利的似然函数,并通过SMC方法实现。通过仿真实验可知当信源数目已知情况下,SS-MeMBer DOA跟踪算法与SS-PAST及PAST跟踪算法相比性能更优。信源数目未知情况下也能准确跟踪数目时变的DOA,与MPP-PHD算法相比,SS-MeMBer算法势估计更准确,OSPA误差更小。总体而言,本文所提的基于空间平滑的多伯努利滤波器DOA跟踪算法,在单快拍量测数据情况下能准确跟踪时变DOA。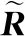

3 SS-MeMBer DOA跟踪粒子滤波实现算法


4 仿真实验

4.1 信源数目固定不变的DOA跟踪

4.2 信源数目时变的DOA跟踪



5 结 论
——以鲁甸地震相关新浪微博为例

