基于抽样的影响力传播成本最小化算法
盛 俊,李 斌,陈 崚
(1.扬州大学 信息工程学院,江苏 扬州 225000; 2.扬州市职业大学 信息工程学院,江苏 扬州 225000)
0 引 言
近年来,随着Twitter、Facebook、谷歌、微博等社交网络的蓬勃发展,网络分析成为社区检测[1]、关系挖掘[2]、度量学习[3]、网络结构分析[4]、链接预测[5]等领域的研究热点。社交网络[6]是由各种实体构成的交流平台,它形成了一个图的结构,图中的顶点为各种实体,连接它们的边反映了它们的相互关系。随着互联网的不断发展,人们使用社交网络也越来越频繁。社交网络中,用户的观点、行为和情感都会受到某些用户影响力的传播作用的影响。而社交网络的流行,也带来了影响力传播的一些新的应用,例如舆情控制[7]、病毒式营销[8]等。因此,如何衡量和预测一个或多个用户对其社交范围内其他用户的影响力是一个关键的问题。影响力最大化[9]就是要在一个社交网络中找出一个影响力的发散源节点,即“种子”集合,使得这些集合中的节点在社交网络中扩散的影响力最大化。影响力最大化在生物信息学[10]、政治选举、病毒营销[11,12]、经济学[13]、推荐[14]、舆情监测[15]等领域得到了广泛的应用。
影响力最大化的问题本质上是一个离散优化问题,常用的传播模型有独立级联模型和线性阈值模型。影响力最大化的问题可以用贪心法来求解。然而,贪心算法的时间复杂度很高,大部分的计算时间用来估计种子集合的影响力范围。因此,随后的很多人对其效率进行了改进。Sun等[16]提出了一种基于有影响力种子接班人的可扩展的影响力最大化方法,算法借助种子顶点接班人的概念,减少了影响力传播的评估次数。
近年来,出现了一些不同的传播模型下的影响力最大化的新的应用问题。SharanVaswani等[17]研究了自适应的影响力最大化问题,提出了自适应的种子选择策略。该方法根据已有种子的传播情况的反馈来选择新的种子。为了有效地利用反馈信息,Yuan等[18]提出了一个部分反馈模型,该模型可以在性能和延迟之间取得平衡。他们验证了部分反馈模型中的影响力扩散函数是非次模的。为此,他们提出了一种(α,β)贪婪的方法可以使得在部分反馈模型中达到常数近似比例的结果。
在病毒营销中,由于顾客对产品的影响力传播能力不同,商家可能会向不同的顾客提供不同的优惠折扣。该问题可以建模为连续影响最大化问题。Yu Yang等[19]研究了这个问题,并提出了一个获得最优种子集的算法。Tang等[20]研究了如何确定病毒营销中各个客户的优惠折扣的问题:给定一个预算值,企业需要决定给予哪些客户优惠折扣,应该给每一个客户提供多少折扣,才能使得产品销售到尽可能多的客户。他们在不同的扩散模型下研究了这一问题,并提出了一种贪心方法,使得影响扩散的期望值充分地逼近最优值。
在上面提到的问题中,种子集的大小或成本是预先定义好的。但在一些实际应用中,影响力的散布者希望通过最少的种子或最低的成本来将影响力传播到一定范围内。已有的研究结果表明该问题不具有次模性,可以使用逼近最优解的近似算法来求解。Zhang等[21]研究了在多个网络中将影响传播到指定范围的最小数目的种子挖掘问题。他们提出了一种将多个网络映射成单个网络的有损耦合方法,并采用改进的贪婪算法检测种子节点。
在影响力最大化的商业应用中,广告的成本往往受到预算的限制。例如,一家通讯设备公司需要在某个地区销售一款新手机,他们可以通过向一些选定的用户提供优惠折扣,以最大限度地扩大其新手机的影响力。公司的目的是鼓励有影响力的客户说服尽可能多的朋友和亲戚购买这款新手机,而该公司在优惠折扣上的成本要降到最低。由于公司对不同的用户所给的折扣可能不一样,该问题的关键是如何选择有影响力的用户,将产品的影响力传播到某个地区范围,而总费用要最小。这就是研究影响力传播的成本最小化问题。近年来,有很多工作研究了这一个问题。
已有的大部分影响力最大化算法需要通过抽样方法来估计影响力传播的范围,这使得算法的复杂度很高。因此,研究影响力最大化以及成本最小化的效率更高的算法很有必要。为此,文中提出基于LT模型的影响力传播的成本最小化算法,该算法利用VC(Vapnik-Chervonenkis)维对网络的路径进行抽样,从而计算它们的激活概率。我们在实际数据集上的实验结果表明,该算法比其它方法具有更高的性能。
1 问题的定义及其性能分析
定义1 影响力传播的成本最小化问题
一个社交网络可用有向图G=(V,E,P) 表示,其中V为节点的集合,E为有向边的集合,P=[pij] 为概率矩阵,设有向边(vi,vj)∈E,P的元素pij表示vi对vj产生影响的概率。在网络的顶点集合V上定义成本函数C(v), 为选用顶点v为种子的成本。给出激活范围U⊆V, 以及一个覆盖阈值η≤|μ|, 我们要找一个使得成本
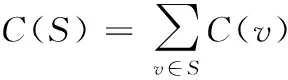
最小的种子集合S,且其在U中的影响力InfU(S) 满足
|InfU(S)|≥η
即要在集合V中选择一个种子集合S*满足
(1)
我们称该问题为影响力传播的成本最小化问题。
顶点v的激活成本C(v) 在实际应用中通常为给种子客户v的折扣优惠,或网站v推销产品的广告费用。这可以根据用户的信誉度、网站的影响力来确定。所有种子的成本之和,构成了种子集合S的成本,此为该产品营销的总成本,我们的目的是要将产品的影响力传播到指定的范围,而总费用要最小。
我们考虑在线性阈值模型下的影响力传播的成本最小化问题。线性阈值模型(LT)将用户分为激活和非激活两种状态,该模型为每个节点v赋予一个阈值θv, 一旦v的相邻节点对它激活值的累计大于θv, 节点v就会变为激活状态。图1表示了在线性阈值模型下影响力的传播方式,其具体过程如下:

图1 线性阈值传播模型
初始时刻t=0,网络中只有种子节点为激活状态。一个节点被激活以后,它会试图激活它的未激活的邻居。一旦节点v所受到的影响力的累计超过阈值θv, 它就转变为激活状态,否则它继续在未激活状态。重复这样的激活过程,直到没有更多的节点可以被激活为止。种子传播的影响力大小即为被激活的节点的个数。
定理1 影响力传播的成本最小化问题是NP-难的。
证明:证明影响力传播的成本最小化问题可以规约为带权集合覆盖(WSC)问题,而WSC问题是NP-难的。
对于带权集合覆盖问题,记U={u1,u2,…,un} 为全集,而B1,B2,…,Bm为U的m个子集。每个子集Bi⊂U(i=1,2,…,m) 具有一个权重w(Bi)。 WSC问题就是要找出具有最小权重的一组子集,使它们的并集覆盖U的至少η个元素。
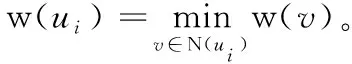
假设S={v1,v2,…,vk} 为影响力传播的成本最小问题的解。如果S∩Y=φ, 我们知道WSC问题中的子集B1,B2,…,Bk至少可以覆盖在u中的η个元素,它们可以形成WSC的问题的一个解。如果Y∩S≠φ, 我们可以将Y∩S中的每一个顶点u用其成本最少的邻居节点v∈N(u) 来代替,从而形成新的子集S′⊂S。 易知C(S′)=C(S), 则S′也是WSC问题的一个解。
可以用类似的方法证明,WSC实例的解也是影响力传播的成本最小问题实例的解。
证毕。
由于影响力传播的成本最小化问题是NP-难的,需要设计一种有效的算法来寻找种子集S,使其近似于最优解S*。我们利用影响力传播的成本最小化问题的传播函数的单调性和次模性,使用贪心方法取得该问题的近似最优解。
定义2 单调性
设f(S) 为集合S的函数,对于两个集合S和Q,若S⊆Q, 有f(S)≤f(Q), 则称f(S) 对于集合S是单调的。
定义3 次模性
设f(S) 为集合S的函数,对于两个集合S和Q以及元素V,若S⊆Q, 有
f(S∪{v})-f(S)≥f(Q∪{v})-f(Q)
则称f(S) 是次模的。
在影响力传播的成本最小化问题中,我们用InfU(S) 表示种子集合S所影响的U中的节点的集合,用传播扩散函数f(S)=|InfU(S)| 表示所影响的U中的节点的数目。
定理2 在影响力扩散传播的成本最小化问题中,传播函数f(S)=|InfU(S)| 是单调和次模的。
证明:
(1)单调性
设X为U中的一个被种子集合S影响的节点, InfU(S,x) 为S中种子的影响力传播到X的路径中U中的被影响的节点的集合, fx(S)=|InfU(S,x)| 为InfU(S,x) 中节点的个数,则有
在这里, Pr(x) 是X被影响的概率。
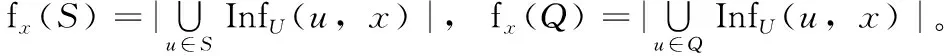
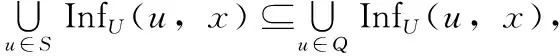
由于f(S) 是fx(S) 的线性组合, f(S) 也是单调的。
(2)次模性
设v∈V为网络中的一个顶点,易知
fx(S∪{v})-fx(S)=|InfU(v,x)InfU(S,x)|fx(Q∪{v})-fx(Q)=|InfU(v,x)InfU(Q,x)|
(2)
由于S⊆Q, 且fx(S) 是单调的,则有fx(S)≤fx(Q)。
那么有
|InfU(S,x)|≤|InfU(Q,x)|
(3)
由式(2)和式(3)可知
fx(S∪{v})-fx(S)≥fx(Q∪{v})-fx(Q)
(4)
这说明了fx(S) 是次模的。由于f(S) 是fx(S) 的线性组合,故f(S) 也是次模的。
证毕。
研究结果表明,若影响力最大化问题的传播扩散函数具有单调性和次模性,则使用贪心算法依次选择影响扩散增量最大的节点,其结果是最优解的 (1-1/e) 近似。因此,基于传播扩散函数f(S) 的次模性,我们可以用贪心法来选取种子集合。
2 路径的激活概率
研究结果表明,LT模型可化为多个“Live-Edge”图(LE图,活边图)来表示。在一个活边图中,每一个顶点v按照连接它的入边的概率随机选取一条入边加入活边图。因此,我们可以将网络看成是一个不确定图,LE模型中的每一种选择可以看成不确定图的一个可能世界。
定义4 不确定图
不确定图是一个三元组G=(V,E,P), 其中p∶E→(0,1) 为边上的存在函数,V和E分别表示为顶点和边的集合。边上的概率P∈(0,1) 表示该边存在的可能性,若图中所有边上的概率皆为P=1, 即该图为确定图。
一个不确定图G=(V,E,P) 含有2|E|个可能世界,可能世界的定义请参见文献[22]。记G的可能世界集合为W(G)。
设G′=(V,E′) 为G的一个可能世界,G′存在的概率为
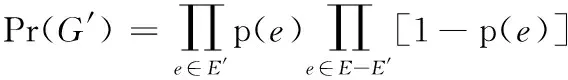
(5)
G的所有可能世界的存在概率之和为1,即

将网络中的每一条边上的传播概率看成边的存在概率,则可以构成一个不确定图,LE模型中的每一种活边图可以看成一个可能世界。这样,S的激活范围σ(S) 就为可能世界中从S的顶点能够连接的U中的范围的期望值。即
(6)
其中, σG′(S) 可以使用下式进行计算
(7)
在式(7)中

结合式(6)和式(7)可以得到

(8)


(9)
则

(10)
由式(10)可见,要计算σ(S) 的值,首先要对S中所有顶点u估计Pr(u) 的值。
3 路径抽样方法
由于Pr(u,v)是从u到v有路径的概率,可用下式计算
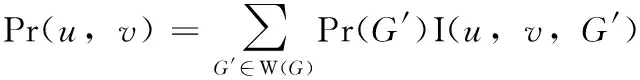
(11)

我们首先估计所需样本的个数。
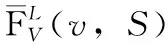
为了估计合适的样本个数r,我们借助于Vapnik-Chervonenkis 维的方法。
定义5 VC维(Vapnik-Chervonenkis dimension)[23]H的VC维记为VC(H)。 VC(H) 是S被H打散的最大的基数。
打散的定义请参见文献[23]。
在这个路径抽样的问题中,实例集S为PL(x), 空间集H即为集合Hx
Hx={px,v|v∈V,|px,v|≤L}
(12)
即长度小于L的以x开头的路径的集合。
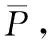
设S={x1,…,xm}为数据集D上根据分布φ而得到的样本集,对于子数据集A⊆D, 设φ(A)为按照分布φ而得到的样本属于的A概率,则在S中对φ(A) 的估计值φS(A) 为
(13)
这里指示函数IA(xi) 定义为
定义6ε近似:设H为D上的一个空间集合,φ为D上的概率分布,设ε∈(0,1),D上满足下列条件的集合S为 (H,φ) 中的一个ε近似
(14)
式中:sup为上确界。根据Vapnik-Chervonenkis 的学习理论可知,我们可以由φ的分布以及H的VC维的值来估计出构造 (H,φ) 的ε近似所需样本的个数。
定理3[24]记H为D上的空间集, VC(H)≤d,φ为D上的一个分布,设ε,δ∈(0,1), 且
(15)
那么,S将以1-δ的概率为 (H,φ) 的ε近似。这里, |S| 是集合S中样本集的大小,常数C>0。
上述定理告诉我们,如果我们估计出VC(H) 的大小,就可以用式(15)计算出QL(x) 中的样本数r,使得QL(x) 以1-δ的概率成为PL(x) 的ε近似。
为此,针对路径抽样问题有如下的定理:
定理4 设H为PL(x) 上的空间集,x为G的某一顶点,H={px,v|v∈V,|px,v|≤L}, 则Hx的VC维满足
Vc(H)≤log2(L+1)
(16)
定理4的证明请参见文献[25]。
由定理4可知,使用H={px,v|v∈V,|px,v|≤L} 的VC维最多为log2(L+1)。 将此值带入式(15)中的d,得到所需样本个数r的取值范围为
(17)
只要取大小满足式(17)的r,就可以保证QL(x) 以1-δ的概率成为PL(x) 的ε近似。
4 算法框架与复杂度分析
综上所述,文中提出算法Sampling_MINSC解决影响力成本最小化问题,Sampling_MINSC算法首先抽样若干个可能世界,然后在此基础上对各个节点估计Pr(u)。 算法取Pr(u)/C(u)最大的若干个节点构成种子集合S,使得在U中的影响力传播超过η, 且成本最小。给定误差阈值ε、 概率值δ、 路径的数学期望的阈值ρ, 算法Sampling_MINSC的总体框架描述如下:
算法1: Sampling_MINSC
输入:G=(V,E,P): 已知网络;
η: 扩散规模;
C: 成本阈值;
输出:S: 达到传播阈值的最小成本种子集合;
(1)由式(17)计算抽样的大小r;
/*构造r个可能世界*/
(2)fori=1 to r do
Sample-generating(G)
end fori;
/*计算每个节点在可能世界中可以到达的范围*/
(3)对图G中所有节点对 (u,v) 置
Pr(u,v)=0
(4)fori=1 to r do
Prob-computing(Gi);
end fori;
(5)forevery nodeu∈Vdo
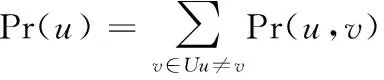
endforu;
(6) InfU(S)=0;
repeat
取Pr(u)/C(u) 最大的节点u;
S=S∪{u};
InfU(S)=InfU(S)+Pr(u);
UntilInfU(S)≥η;
(7)returnS
算法Sampling_MINSC的步骤1由式(17)计算抽样个数r;第(2)步调用算法3产生r个抽样;第(3)步和第(4)步调用算法2估计各个顶点能够到达的范围。第(5)步对各个顶点计算Pr(u)。 第(6)步和第(7)步取Pr(u)/C(u) 最大的若干个节点构成集合S并输出。
算法第1步计算抽样个数r,所需时间为O(1); 第(2)步调用算法2,复杂度为O(r*m), 其中m=|E|。 第(3)步复杂度为O(n2), 其中n=|V|。 第(4)步调用算法Prob-computing,所需时间为O(r*n2)。 第(5)步累加所有顶点Pr(u) 值,需要O(n2) 时间。第(6)步构成集合S,设最终S中有P个种子,p≤n, 则复杂度为O(np)。 第(7)步输出S,复杂度为O(p)。 综上所述,算法的复杂度为O(n2)。
算法Prob-computing计算G所有顶点对u、V计算Pr(u,v) 的值。其内容如下:
算法2: Prob-computing
输入:Gi: 已知的抽样图;
L: 路径长度阈值;
输出: Pr: 节点之间的Pr(u,v) 的值;
(1)foreachv∈Vdo
(2)u=v;l=0;Q=φ;
(3)whileQ≠φandl≤Ldo
(4)foreach unvisited neighborwofudo
(5) put (w,l+1) into the tail ofQ;
(6) Pr(u,v)=Pr(u,v)+Pr(Gi);
(7)endforu;
(8) get the head ofQ→(u,l);
(9)endwhile
(10)endforv
算法Sample-generating 对图G的边进行抽样,从而产生一个可能世界,具体步骤如下:
算法3: Sample-generating
输入:G=(V,E,P): 已知网络;
输出:G′=(V,Ek): 所产生的一个可能世界;
(1)Ek=φ
(2)forevery edgee=(u,v) inEdo
(3) 产生随机数r∈(0,1);
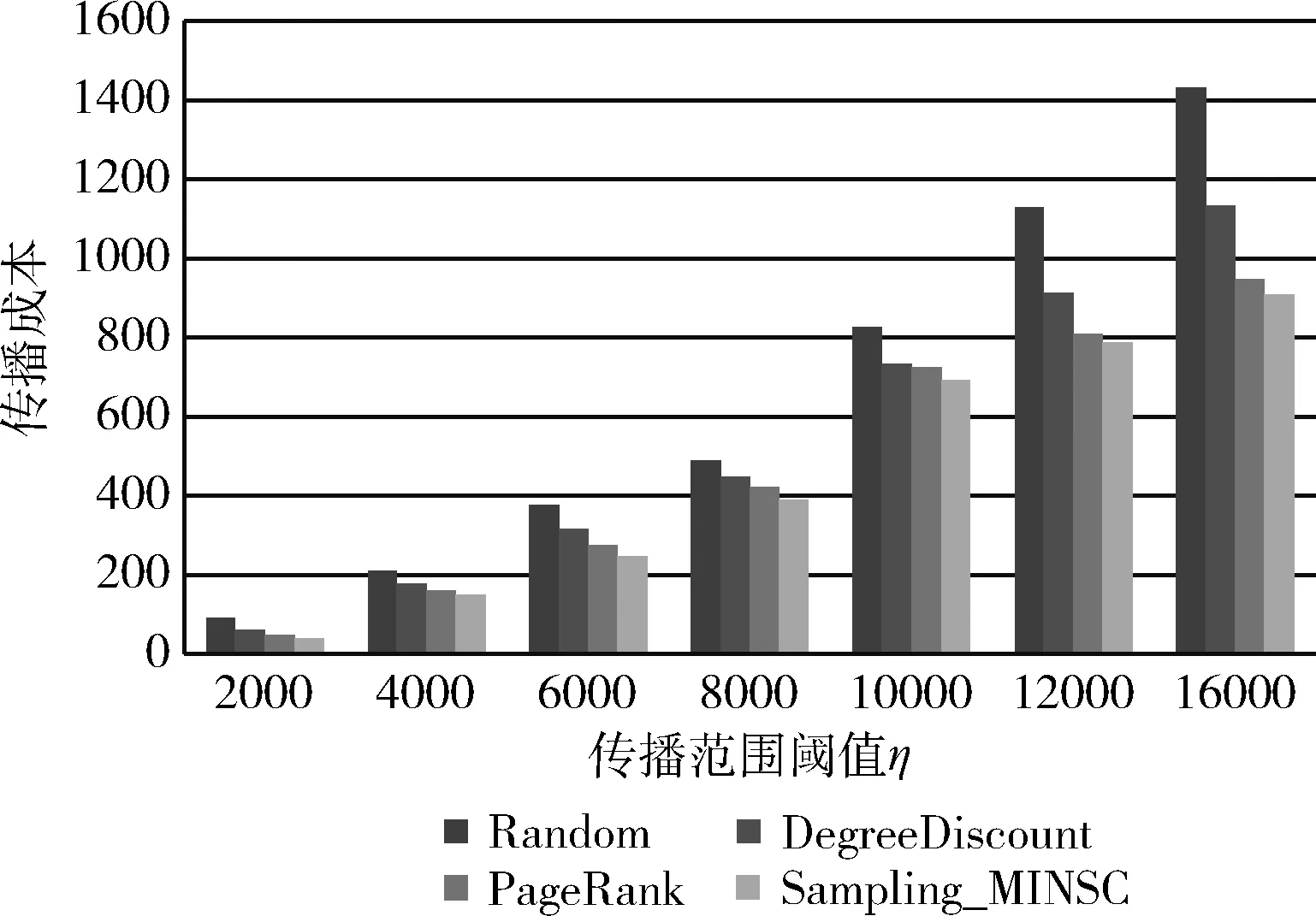
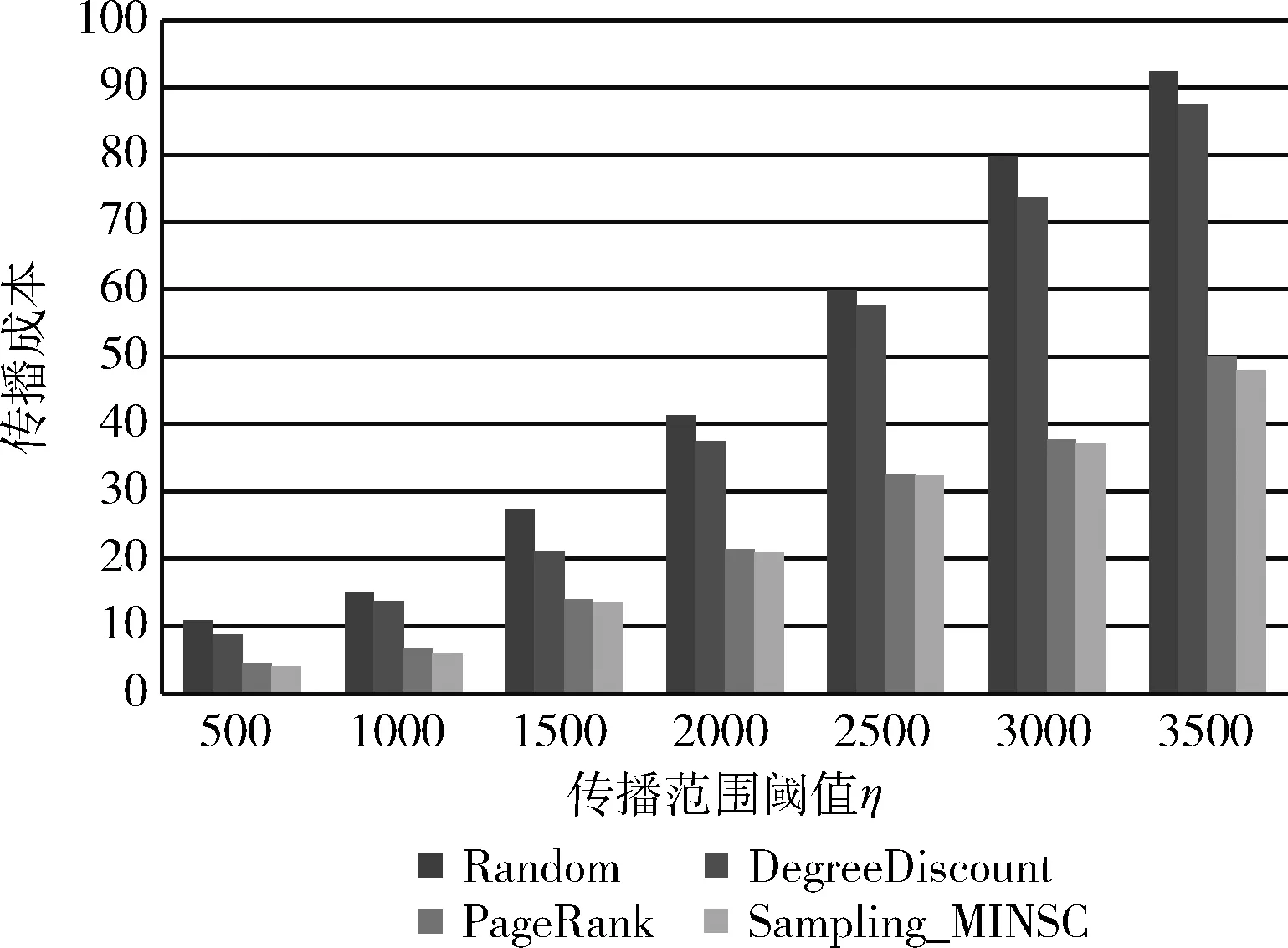
(4)ifr (5)Ek=Ek∪{e} (6)endif; (7)endfore; (8)G′=(V,Ek); (9) returnG′ 我们在4个数据集上对上述算法的性能进行测试。实验数据集见表1。 表1 实验数据集 数据集DBLP来自一个论文作者的网络,网络中的顶点为作者,顶点间的连边说明他们共同发表过论文。和DBLP类似,数据集NetHPET来自一个高能物理论文作者的网络。Epinions是一个对商品进行评价的网站,用户可以对商品发表评论,或对其他用户的评论发表意见。从用户之间的不同意见可以决定他们之间的关系。数据集LiveJournal来自一个在线社区,其中节点表示会员,会员通过个人日志和组日志来标志和其他成员的朋友关系。 我们对算法用Matlab编程,在Windows7环境下运行,处理器为Core i5 2410 M 2.3 GHz,16 GB内存。 对上述数据集,顶点间的传播概率设置为 节点的激活阈值θv设置为 [0,1] 中的一个随机值。对每个节点v产生一个 [0,1] 间的随机数作为它的成本值C(v)。 在实验中,我们将所提出的算法的性能和Greedy、PageRank[26]、DegreeDiscountIC[15]和Random等算法进行比较。Greedy是一种贪心算法,它逐次选择影响力增量最大的顶点加入种子集合。PageRank采用迭代的方法计算节点的影响力,并挑选影响力最大的若干个顶点为种子顶点。算法DegreeDiscountIC采用贪心法根据顶点的度来选择种子集合。和Greedy算法不同的是,当顶点v的相邻顶点被选作种子后,算法要对节点v的度数适当降低。Random算法在顶点集合中随机挑选k个顶点作为种子顶点。 (1)DBLP数据集上的结果 在DBLP上抽出1 737 893个可能世界进行实验,实验结果如图2所示。 图2 DBLP上的运行结果 由图2可以看出,达到相同的影响力覆盖范围时,提出的算法Sampling_MINSC所用的成本最少,PageRank和Sampling_MINSC的成本总体上相近,略小于Sampling_MINSC。DegreeDiscountIC次之, Random最差。 (2)Epinions数据集上的结果 我们在Epinions数据集上进行1 737 893次抽样,所得到的传播成本如图3所示。 图3 Epinions上的运行结果 由图3可以看出,Sampling_MINSC算法依然是最优的,PageRank次之,DegreeDiscountIC和Random的效果较差。 (3)NetHPET数据集上的结果 我们在NetHPET数据集上进行1 737 893次抽样,所得到的传播成本如图4所示。 图4 NetHPET上的运行结果 实验结果显示,提出的算法Sampling_MINSC所用的成本最少,PageRank和Sampling_MINSC的成本总体上相近,略小于Sampling_MINSC。DegreeDiscountIC次之, Random最差。 从上述实验结果可以看出,相较于PageRank、DegreeDiscountIC和Random,Sampling_MINSC算法的效果是最好的。Sampling_MINSC算法之所以影响传播代价最小,是因为它采用了贪心算法使得种子的影响力尽可能覆盖较多的目标范围。另外,它采用基于抽样的方法从抽样的子图中得到种子集,能较准确地逼近原网络。 对算法Sampling_MINSC在Epinions数据集上对于不同的概率p下的成本进行比较。设误差界为ε=0.01η, 图5显示了在各种传播范围阈值η下,对于不同的概率p的成本。由图5可以看出,对于较大的概率p,由于所要覆盖的范围较大,所需的成本较高。 图5 Epinions数据集上不同的概率p下的成本 对算法Sampling_MINSC在Epinions数据集上对于不同的误差界ε下的成本进行比较。设概率值p为0.9,图6显示了在各种传播范围阈值η下,误差界为ε=0.01η、0.02η、0.05η、0.1η时的成本。由图6可以看出,对于较大的ε值,由于覆盖的精确度要求较高,所需的成本较高。 图6 Epinions数据集上不同的误差界ε下的成本 针对影响力传播的成本最小化问题,提出Sampling_MINSC算法。算法基于不确定图的可能世界的概念进行路径的抽样,使用VC维去估计可能世界的抽样数量,这样可以避免使用Monte Carlo模拟来计算度量影响力扩散。使用贪婪算法在固定影响范围下筛选出具有最小成本的种子集合。我们通过实验来验证文中所提算法的准确性,并和其它类似算法进行比较。此外,还对算法在不同的概率p下的成本、在不同误差界ε下的成本进行比较。实验结果表明,Sampling_MINSC算法的传播代价比其它算法小。Sampling_MINSC算法之所以影响传播代价最小,是因为它采用了贪心算法使得种子的影响力尽可能覆盖较多的目标范围。另外,它采用基于抽样的方法从抽样的子图中得到种子集,能较准确地逼近原网络。5 实验结果及其分析
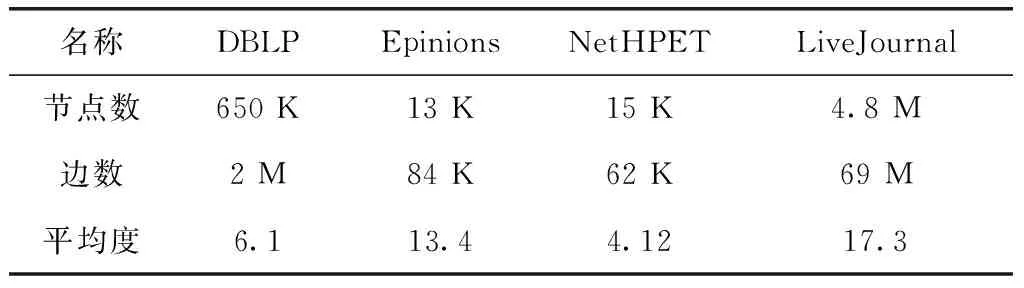
5.1 实验数据集和相关设置
5.2 算法对比
5.3 实验结果



6 结束语

