基于灵敏度分析的可靠性增长规划优化设计

李中生，秦红星

(唐山学院 河北省智能装备数字化设计及过程仿真重点实验室，河北 唐山 063000)

0 引言

可靠性增长规划是实施可靠性增长管理的重要依据，绘制可靠性增长规划曲线是可靠性增长规划的重要组成部分。可靠性增长规划曲线为可靠性测试提供了临时的里程碑，用以判定可靠性增长测试方案是否合理。可靠性规划曲线一般由可靠性增长规划模型生成，可直观地描述可靠性增长规划的整个过程。

1956年，美国学者Weiss建立了一个理想化的可靠性增长过程数学模型，该模型是可靠性增长技术的雏形[1]。1964年，Duane提出了一种学习曲线方法，用于监测机电系统的可靠性增长程度并预测其可靠性增长进程[2]。1970年Selby和Miller将Duane假设扩展为一种动态的规划工具，可以根据事先设定的增长率预估系统在未来一段时间内的平均故障间隔时间(Mean Time Between Failure，MTBF)[3]。基于预测方法的规划模型(Planning Model Based On Projection Methodology，PM2模型)[4]是一种被广泛使用的可靠性增长规划模型，其主要特点是规划曲线在任何给定的可靠性增长试验持续时间内都能达到设定的可靠性目标值，从而获得了试验决策者的推崇。PM2模型是一种基于项目里程碑式的规划模型，试验管理部门通过制定必须实现的测试目标并充分利用现有的测试资源进而确定可靠性增长试验的增长率。自2009年6月以来，PM2模型一直是美国陆军产品开发测试计划中的一项具体要求[5]。

国内外学者已经对可靠性增长规划模型的固有参数开展了许多有价值的研究，如1990年美国的Ellner和Trapnell发布了一系列针对不同武器装备和不同实验条件下的总平均值为0.69的改进有效性系数(d)的参考值[6]；2013年Calomeris和Herbert指出，不同的试验持续时间和系统初始MTBF值(Initial MTBF,MI)以及不同的目标MTBF值(Final MTBF,MF)都将生成不同形状的规划曲线[7]；2014年Crow指出，对于完全由新技术构成的武器系统，管理策略参数可以取较大的数值，如0.95，而对于在设计中使用原有技术的其他系统，管理策略参数应取较小的数值[8]；2015年Awad对系统的初始故障率展开了灵敏度分析[9]；2019年李中生等对PM2模型的多个参数进行了单参数灵敏度分析[10，11]。

现有文献对PM2模型的规划曲线与其两个过程管理参数乘积之间的关系研究较少，而这两个过程管理参数的乘积将直接决定可靠性增长试验的成败，为此本文研究了PM2规划曲线与两个过程管理参数乘积之间的关系，并推导出了这两个参数乘积的通用取值范围。

1 PM2模型和参数

PM2模型的各参数和数学表达式如下：

(1)d：改进有效性系数。d属于可靠性增长试验的过程管理参数，表征纠正措施的有效程度，其取值范围一般为[0.6，0.8]。

(2) MS：管理策略，也属于过程管理参数。MS是指系统的B类故障率与系统的初始故障率之比，常用取值范围为[0.7，0.95]。其中B类故障是指如果在可靠性增长试验中发生，则被确定为需要进行纠正的那些系统性故障。相反地，即使在可靠性增长试验中被发现也不进行纠正的系统性故障及所有的残余性故障，称为A类故障。且有：

(1)

其中：λA为A类故障所导致的系统失效率；λB为B类故障所导致的系统失效率。

(3)MI：系统的初始平均故障间隔时间，表示为：

(2)

其中：λI为系统的初始失效率。

(4)MF：系统经历可靠性增长试验后最终可实现的平均故障间隔时间，属于试验设计参数。

(5)MGP(Growth Potential，GP)：系统可实现的最大平均故障间隔时间，表示为：

(3)

(6) GPDM(Growth Potential Design Margin)：系统的增长潜力比,表示为：

(4)

由于测试时间和成本的限制，MF的值通常会小于MGP值。根据历史经验，GPDM的最大值约为1.5。根据式(3)和式(4)，单次可靠性增长试验增长率(MF/MI)的取值范围约为[1.5，3.0]。如果要求的试验增长率超出此范围，则可靠性增长试验应分阶段进行。

(7)λ(t)：系统在时间t(t为测试持续时间)时的预期失效强度,表示为：

λ(t)=λA+(1-d)λB+d·h(t).

(5)

其中：h(t)为新的B类故障在时间t内发生的概率,对于PM2模型，其定义式为：

(6)

其中：βPM2为hPM2(t)的形状参数,且有：

(7)

其中：T为参数，表示可靠性增长试验设计持续时间，属于试验设计参数。联合式(5)～式(7)可得：

(8)

联合式(1)和式(2)可得：

(9)

对于一个给定的目标值，式(8)可转换为：

(10)

显然有d·MS·MF-(MF-MI)>0，即：

(11)

对式(10)进行化简可得：

(12)

式(12)表明，对于PM2模型，无论过程管理参数d和MS取何值，只要测试持续时间t等于试验设计持续时间T,试验目标总能够达到。

2 参数灵敏度分析

2.1 试验设计持续时间灵敏度分析

假设某待测试系统的初始平均故障间隔时间MI为100 h,目标平均故障间隔时间MF为150 h,且两个管理参数的乘积(d·MS)为0.7。令可靠性增长试验设计持续时间T分别等于9 000 h、10 000 h、11 000 h、12 000 h，依据式(10)可得可靠性增长规划曲线,如图1所示。

由图1可见，可靠性增长测试将在T=9 000 h结束；可靠性增长测试将在T=10 000 h时达到目标值；可靠性增长测试将在T=11 000 h时达成目标；可靠性增长测试将在T=12 000 h时达到预期值，即参数T作为一个重要的主观输入的试验设计参数，将决定可靠性增长试验何时结束以及何时满足试验预期。

2.2 单次增长率为1.5时的参数灵敏度分析

假定某系统的初始平均故障间隔时间MI为100 h，目标平均故障间隔时间MF为150 h，且试验设计持续时间T=10 000 h。令(d·MS)分别等于0.33、0.34、0.54、0.74，由式(10)可得可靠性增长规划曲线，如图2所示。

由图2可见，两个过程管理参数的乘积d·MS对可靠性增长规划曲线有很大的影响，d·MS=0.34时的规划曲线描述了在可靠性增长试验过程中，由于对所发生故障持续地整改，系统由初始的失效率逐步增长到目标失效率的过程；d·MS=0.33时的规划曲线描述了在可靠性增长试验过程中，系统的失效率由初始失效率急速增长为无穷大，之后突变到无穷小，然后逐渐增长到目标失效率，这表明在特定的试验条件下，两个过程管理参数的乘积d·MS存在最小值。对于本例由式(11)可得最小值为1/3，即d·MS的值需大于此最小值，否则可靠性增长试验的结果不能满足目标值。

2.3 单次增长率为2.0时的参数灵敏度分析

令某系统的初始平均故障间隔时间MI为100 h,目标平均故障间隔时间MF为200 h,试验设计持续时间T为10 000 h。d·MS分别取0.49、0.51、0.71、0.91，据式(10)可得可靠性增长规划曲线，如图3所示。

同理，当d·MS=0.49时可靠性增长规划试验的规划曲线无法用常理解释。对于本例由式(11)可得d·MS最小值为1/2，即d·MS的值必须大于此最小值。

2.4 单次增长率为3.0时的参数灵敏度分析

令某系统的初始平均故障间隔时间MI为100 h,目标平均故障间隔时间MF为300 h,且试验设计持续时间T为10 000 h。d·MS分别取0.66、0.67、0.77、0.87，据式(10)可得可靠性增长规划曲线，如图4所示。

图1 不同参数T对应的 图2 增长率为1.5时不同 图3 增长率为2.0时不同 图4 增长率为3.0时不同 可靠性增长规划 d·MS值对应的可靠性增长 d·MS值对应的可靠性增长 d·MS值对应的可靠性增长 曲线 规划曲线 规划曲线 规划曲线

对于本例由式(11)可得最小阈值为2/3，即d·MS的值必须大于此最小值，否则可靠性增长试验的结果不能满足可靠性增长规划的目标值。

3 实例

某公司拟对现有的机械手系统开展可靠性增长试验，以增加其使用可靠性和平均故障间隔时间，试验设计参数和过程管理参数由项目管理部门确定，原始可靠性增长规划数据见表1。

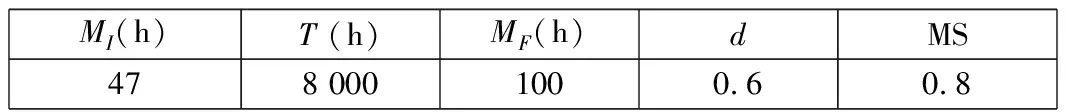
表1 原始可靠性增长规划数据

经过漫长的可靠性试验后，质检部门发现实际平均故障间隔时间并未达到目标值，为此公司组织开展原因分析，但始终找不到根本原因。作者按式(11)对此次可靠性增长试验做如下判别：

d·MS=0.48<1-MI/MF=0.53.

即两个过程管理参数乘积d·MS的取值不合理。随后提出两种改进方案：①公司需提高过程管理参数MS到0.9，要求公司加大B类故障的认定比例，并按照公司一贯的改进有效性系数d对试验过程中所发生的B类故障进行改进；②公司需提高过程管理参数d到0.7，即公司需提高对B类故障的改进手段。

图5为按照原始的试验过程管理参数绘制的可靠性增长规划曲线。在可靠性增长试验开始后，系统的MTBF由初始值(MI=47 h)先缓慢而后急速减小为负无穷大，之后突变到正无穷大，然后先急速而后缓慢降低到目标值(MF=100 h)，系统MTBF突变的时间点约为t=1 451.5 h。这种不合理现象是由于式(10)的分母为负数所致。

图5 原测试方案的可靠性增长规划曲线

表2为方案修改后的可靠性增长试验规划数据。图6为改进后的可靠性增长规划曲线。

表2 修改后的规划数据

由图6可知，在整个可靠性增长试验过程中，方案1的即时MTBF值总是大于方案2的即时MTBF值，因此如果两种方案都能满足要求，则建议优先选择方案1。

图6 改进测试方案后的可靠性增长规划曲线

4 结论

本文对PM2模型的参数开展了灵敏度分析，发现对于既定的测试方案，两个过程管理参数的乘积 (d·MS) 均存在取值下限。基于此，本文推导了其通用的取值范围，并通过实例验证了取值范围的有效性。根据研究，可以得出以下结论：

(1) PM2模型的两个过程管理参数的乘积，对于可靠性增长规划有很大的影响。

(2) 对于每一个既定的可靠性增长规划测试方案，PM2模型的两个过程管理参数的乘积均有一个确定的取值范围，如果实际值脱离此范围，将导致可靠性增长规划测试失败。

(3) 通过预先判断PM2模型的参数取值，可以降低未达成测试目标的风险。即如果发现两个过程管理参数的乘积小于其取值下限，则应在可靠性增长试验开始前予以调整。